Annexe B
Dynamiques temporelles

6
4
2
0
8
A
X1
X2 X3

12
B
10
8
6
4
2
0
0 200 400 600 800 1000
Temps
15
10
5
0


C
1700 1800 1900 2000
Temps
1700 1800 1900 2000
Temps
8

D
6
4
2
0
2700 2800 2900 3000
Temps
FIG. B.1 - Dynamiques temporelles rencontrées dans le
modèle R-M au fil de l'enrichissement du système de A a D. Ces
évolutions correspondent aux dynamiques dans l'espace des phases
présentées sur la figure (Fig. 5).
Ces graphiques permettent de mieux visualiser les temps de
parcours des attracteurs, c'est a dire les schémas
répétitifs de la dynamique, tant pour le modèle R-M que
pour le modèle DEB. Le régime transitoire est inclue
pour le premier cas (A) mais absent des autres.
ANNEXE B. DYNAMIQUES TEMPORELLES
A
X1
X2
X3
30
B
25
20
15
10
5

0
9000 9200 9400 9600 9800 10000
Temps
0 200 400 600 800 1000
Temps

80
C
60
40
20
0
7000 7200 7400 7600 7800 8000
100
D
80
60
40
20
0
9000 9200 9400 9600 9800 10000


Temps Temps
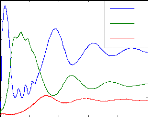
FIG. B.2 - Dynamiques temporelles rencontrées dans le
modèle R-M au fil de l'enrichissement du système de A a D. Ces
évolutions correspondent aux dynamiques dans l'espace des phases
présentées sur la figure (Fig. 7).
Annexe C
La méthode semi-numérique
Voici le détail de la méthode employée
pour calculer les valeurs des équilibres et tester leur stabilité
dans le cas du modèle DEB a 2 échelons. Cette méthode
présente la particularité d'allier des calculs analytiques
traditionnels a des algorithmes informatiques.
L'existence des équilibres est tout d'abord
testée numériquement pour les différentes valeurs des
paramètres de bifurcation en regardant si les valeurs des
variables d'état atteintes au point d'équilibre sont conformes
aux hypothèses biologiques:> 0 et pour les réserves < 1. Le
calcul de la matrice jacobienne permet de déterminer
numériquement la stabilité de ces points d'équilibre
suivant les paramètres de bifurcation. Cette matrice est
obtenue en dérivant sur chaque ligne une équation du
modèle en fonction de chacune des cinq variables en colonne.
?
? ? ? ? ? ? ? ? ? ?
J=
)
_(ÿlb+JXm1X1Xk1
0
_JXm1X0
(Xk1+X0)2 Xk1+X0
ÿkE1 0
ÿkE1
Xk1
(Xk1+X0)2
0 g1( ÿkE1+
ÿkM1)
ÿkE1e1--
ÿkM1g1
(e1+g1)2 x1 e1+g1 _ lb ÿ _
JXm2X2Xk2
(Xk2+X1)2 . . .
0 0
ÿkE2
Xk2
(Xk2+X1 )2
0 0 0
?
? ? ? ? ? ? ? ? ? ?
lbÿ
0 0
0 0
. . .
0
_JXm2X1
Xk2+X1
ÿkE2 0
ÿkE2
e2-- ÿkM2
g2
e2+g2
g2
(ÿkE2+ÿkM2)
(e2+g2)2 x2
Le calcul numérique des valeurs propres de cette
matrice pour les valeurs des points d'équilibre permet ensuite de tester
leur stabilité : si la plus grande partie réelle des valeurs
propres est négative, alors l'équilibre sera stable, sinon il
sera
ANNEXE C. LA MÉTHODE SEMI-NUMÉRIQUE
instable. La confrontation ensuite des zones d'existence, de
stabilité et d'instabilité pour différentes valeurs des
paramètres de bifurcation permet de produire des figures comme la figure
6.

| 


