4.1.3 Visuelle Bildinterpretation
Die visuelle Interpretation besteht darin, das Orthofoto
auszuwerten, indem die Objekte auf dem Bild aufgrund von zusätzlichen
erfahrungsbasierten Informationen wie Textur, Struktur, Form, Kontext und
Reflexion bestimmt werden (Albertz 2001: 126.; Hildebrandt 1996: 291). Hier
spielt auch der Kenntnisstand den Luftbildinterpreten über das
Gelände und dessen Beschaffenheit sowie die Erfahrung des Interpreten eine
wichtige Rolle (vgl. Albertz J. 2007).
In dieser Arbeit wurde die visuelle Interpretation in zwei
Phasen durchgeführt. Zuerst wurden die Objekte erkannt. Als
zusätzliche Informationsquelle zum Orthofoto wurde der Stadtplan
(1:15.000) für die visuelle Interpretation genutzt. Die Gebäude
wurden als Flächen digitalisiert und in drei Klassen unterteilt.
4.1.4 Genauigkeitsbewertung der Klassifizierung
Nach der Klassifizierung wurde eine Konfusionsmatrix
berechnet. Sie hatte zum Ziel, die Korrektheit der Klassifikation im
Zusammenhang mit den Trainingsgebieten zu kontrollieren. Auf Basis der
Konfusionsmatrix konnten verschiedene Genauigkeitsindikatoren (lokal und
global) bestimmt werden, die die Beziehungen zwischen den Trainingsgebieten und
dem
20
Klassifikationsergebnis verdeutlichten (vgl. Zhou 2001). Die
wichtigsten Indikatoren waren die Gesamtgenauigkeit und der Kappa-Parameter.
· Die Gesamtgenauigkeit (Overall Accuracy - OA)
bildet das Verhältnis von korrekt klassifizierten Bildpixeln zur
Gesamtzahl aller betrachteten Pixel ab. Nach Congalton & Green, 1999: 4
lautet die Formel:
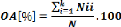
wobei
Nii = Summe der richtig klassifizierten Pixel (in Reihe
i und Spalte i), K = Anzahl der Klassen
N = Gesamtzahl der Pixel der Referenzdaten
· Kappa ist eine Kenngröße
zur Bewertung der Gesamtgenauigkeit (Jamil 2010:50). Dadurch kann die
Qualität abgeschätzt werden, die sich weiter aus der Differenz
zwischen den richtig klassifizierten Pixeln und nicht korrekten
Übereinstimmungen berechnen lässt (Jamil 2010: 52; vgl. Cohen 1960;
Hudson & Ramm 1987). Kappa wird nach folgender Formel berechnet:
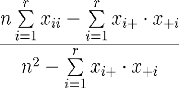
wobei
r = Anzahl der Zeilen der Fehlermatrix
xii = Anzahl der Pixel in der Diagonalen (korrekt
klass.) xi+ = Summe aller Pixel einer Zeile (klassifizierte Werte)
x+ = Summe aller Pixel einer Spalte (Referenzdaten) n = Summe aller
Pixel der Matrix
21
Der Kappa-Koeffizient kann unterschiedliche Werte zwischen -1
bis 1 annehmen. Wenn er komplett mit der Klassifizierung und den Referenzdaten
übereinstimmt, beträgt er 1, bei keiner Übereinstimmung -1.
Dieser Wert wird in der Literatur unterschiedlich bewertet (Jamil 2010). Es
wurde herausgefunden, dass ein Kappa-Koeffizient von über 0,8 ein sehr
hoher Wert der Übereinstimmung ist (vgl. Altmann 1991). Landis & Koch
(1997) haben für den Kappa-Koeffizienten drei Kategorien definiert:
· ausgezeichnet : 0,81 - 1
· sehr gut: 0,61 - 0,8
· gut: 0,41 - 0,6
Ortiz et al. (1997) erstellte folgende Skala:
< 0,0 Sehr schlecht
0 bis 20 Schlecht
20 bis 40 Akzeptabel
40 bis 60 Gut
60 bis 80 Sehr gut
80 bis 100 Ausgezeichnet.
Für die vorliegende Arbeit wurde die Skala von Ortiz et al.
als Referenz verwendet, weil diese
mehr Klassen als diejenige von Landis & Koch (1997)
besitzt.
| 


