Equations differentials stochastics involving fractional brownian motion two parameter

Chapter 2

Stochastic Integration with

Respect to Two-parameter

Fractional Brownian Motion

2.1 Pathwise Integration in Two-parameter Besov Spaces

The next result gives an estimate of the Stieltjes integral for smooth functions in terms of Hölder norms and represents the essential step for extending the Stieltjes integral to Hölder functions of two variables.

Proposition 2.1.1. Let ái + âi > 1, ái, âi ? (0, 1], f, g ? C²(T) and let 0 < åi < ái + âi - 1. Then

i

~~~~

b1lb2 f (t1,t2)dg(t1,t2) a1 L

(2.1)

= C(ái, âi)kgkT,â1,â2 {1f1T,á1,á2(b1 - a1)^á1+â1(b2 -a2)^á2+â2 +1f(., a2) [a1,b1],á1(b1 - a1)^1+å1(b2 - a2)^â2

+1f(a1, .) [a2,b2],á2(b1 - a1)^â1(b2 - a2)^1+å2 + |f(a1, a2)| (b1 - a1)^â1(b2 - a2)^â2}

Moreover, for every partition Ä = (si, _tj)i,j, a1 = s1 < ... < sn1 = b1, a2 = t1 < ... < t_n2 = b2, 1Ä1 = max(si+1 - si) + max(tj+1 - tj) , we have

i j

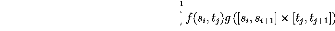
b1

f

b2 n1-1n2-

1

f(

74

,u2)dg(u1,u2) -

E E f(si, tj)g ([sisi+1] × [tj, tj+1])

fa1 a2 i=1

j

=1

(2.2)

+ ~kgkT,â1,â2 + kg(a1, .)k[a2,b2],â2kÄk^á1~ = C(ái, _{âi)kfkT,á1,á2} ~kgkT_,â_1,â₂kÄk^{á1+â1+á2+â2?2}

+ (1g1T,â1,â2 + kg(., _{a2)1[a1,b1],â11Älá2)]} .

Proof. Assume first that f = 0 on ?1T and define

h(t1, t2) = g(b1 - t1, b2 - t2) - g(b1 - a1, b2 - t2)

-g(b1 - t1, b2 - a2) + g(b1 - a1, b2 - a2). (2.3)

Then

Z _b1 Z b2 f(t1, _t2)?²g(t1, t2) dt1dt2 = ?²(f * h)(b1, b2) . ?t1?t2 ?t1, ?t2

a1 a2

Choose åi > 0, 0 < á⁰_i < ái, 0 < â0 i < âi with á⁰_i + â0 i = 1 + åi. By proposition the function f1 = D_a^á+^' f, h1 = D_a^â+^' h are in L₈ and satisfy

Iá0 = f , I_a^â+^" h1 = h. (2.4)

Then by proposition, 2.3 and 2.4 we have

Z _b1 Z b2 Z _b1 Z b2 f(t1, _t2)?²g(t1, t2)

f(t1, t2)dg(t1, t2) = dt1dt2

?t1?t2

a1 a2 a1 a2

?²(f * h)(b1, b2)

=

?2

_{h i}

_Iá⁰

a+f1 * Iâ0

a+h1 (b1, b2)

?t1?t2

=

?t1?t2

?2 _hi

_Iá⁰+â⁰

= _a+ (f1 * h1) (b1, b2)

?t1?t2

?2 ~I1

= _a+I^å_a+(f1 * h1)] (b1, b2)

?t1?t2
?2

= I^å _a+(f1 * h1)(b1, b2),

?t1?t2

= Ia(+ 1,1)_, å₌

such that Ia1+ Iå1,å2

_a+

and then

~Z

kf1 * h1k8

(b1 - a1)^1+å1(b2 - a2)^1+å2

= å1å2(å1)(å2) kf1k8kh1k8.

~Z ^{b2 b1} ~~~~ = (b1 - a1)^å1(b2 - a2)^å2
~~ f(t1, t2)dg(t1, t2) å1å2(å1)(å2)
a1 a2

Next, the integration by parts for functions of two variables (see[9]) yields

f1(x1, x2) = (1 - á^'o(1 - á^'2) fa x

, " (1 - t1 )á 4 (x2 - t2)^á4

1

r

2df ([t1,x1]× [t2,x2])

1 f ([t1,x1] × [t2, x2]) lim (1 ? áo(1 ? t%?x% (x1 - t1)^á4 (x2 - t2)^á4

lirn

x1 f ([t1, x1] [t2, x2])_,

- dt1
t2?x2 fa1 (x1 t1)^á1 (x2 - t2)^á2

x2 f ([t1, x1] × [t2, x2]) dt

lim

-

t1?x1 L2 (x1 _t1)á4 (x2 - t2)á2 2

f2 f ([t1,x1] × [t2, x2])

a1 a2 (xi - t1)^á4+1(x2 - t2)^á2+1

, dt1dt2}

+ác_.á⁰2

,0

á1u2 ix2 f ([t1,x1] × [t2, x2])

t, d dt
(1 - áo(1 - j_a2x1-t1)^á4+1(x2 t2)^á2+1

i 2,

so that

kf1k8 =

,0 á1u2 (1 ? ác)(1 ? T,á1,á2

(2.6)

x1 _fx2

× (x1 - t1 -á4-1 (x2 - t2)^á2-á4-1dt1dt2

a2

= - a1)^á1-á4(b2 - a2)^á2-á4.

Similary

- a1)^â1-âc(b2 - a2)^â2-â. (2.7)

By using (2.6) and (2.7) in (2.5) we obtain (2.1) if f = 0 on ?1T. If f is not necessarily null on ?1T then we define

f(t1,t2) = f ([a1,× [a2, t2])

Then f = 0 on ?1T and f, f have the same increments. Then we have

J b1 1b2

a2 f (t1,t2)?2 g(t1 t2)

?t1?t 2 dt1dt2

Z _b1 Z b2 Z _b1 Z b2

f(t1, _t2)?²g(t1, t2) f(a1, _t2)?²g(t1, t2)

= dt1dt2 + dt1dt2

?t1?t2 ?t1?t2

a1 a2 a1 a2

+ fa1 a2

b1

f

b

2

f(t1, a2)?2g(t1,

?t1?t2

t2) dt1dt2 + f (a1, a2)g(([a1,b1]× [a2, b2]))

,,

= I2 b2 f (t1,t2)?2 g(t1, t2)

dt1dt2 + ^b2 f(a1, t2) r?g(b1 t2) ?g(a1 ?t2 ?t2

t2) 1 dt2

a1 ?t1?t2

a2

a

?g(t1,b2) ? g(t1, a2)1 dt1 + f (a1, a2₎g(([a1,b1]×[a2, b2])

f21 ^b1 f(t1a2) [ ?t1

4

Jk.

k=1

(2.8)

From the previous reasoning we have

ja1 ^b1 l_a:² f (t1, t2) ?²g(t1 , t2)

dt1dt2

?t1?t2

= C(ái,âi)kfkT,á1,á2kgkT,â1,â2(b1 - a1)^á1+â1(b2 - a2)^á2+â2. (2.9)

Next by using (1.3) we have

~~Z b2 ~?g(b1, t2) ~

|J2| =

- ?g(a1, t2) ~~~~

~~ [f(a1, t2) - f(a1, a2)] dt2

?t2 ?t2

a2

+ |f(a1, _a2)g ([a1, b1] × [a2, b2])|

= C(ái, âi) kf(a1, .)1[a2,b2],á2kg(b1,.) - g(a1, .)k[a2,b2],â2 (b2 - a2)^1+å2

+ |f(a1, a2)| 1g1T,â1,â2(b1 - a1)^â1(b2 - a2)^â2,

so that

11 J2 11= C(ái, âi)11g1IT,â1,â2 { If(a1, .)1[a2,b2],á2 (b1 - a1)^â1(b2 - a2)^1+å2 + | f (a1, a2)| (b1 - a1)^â1(b2 - a2)^â2 1.

(2.10)

Similarly

n11J311 = C(ái, _{âi)1g1T,â1,â2} If(., a²)1[a1,b1],á1 (b1 - a1)^1+å1(b2 - a2)^â2 +|f(a1, a2)| (b1 - a1)^â1 (b2 - a2)^â2}.

(2.11)

Replacing (2.10) and (2.11) in (2.8) we obtain (2.2). Next we have

a¹ (12

IÄ f (u1,u2)dg(u1, u2) - E f (si,tj)g ([sisi+1] ×

= Ib1 b2

f

=E

[f(u1, u2) - f(si,tj)] dg(u1, u2)

i,j

=E

i,j

isi+1 itj+1

+E

+E

jsi+1 itj+1

jsi+1 itj+1

[f(u1,u2) - f(u1, tj) - f(si,u2) + f(si,tj)] dg(u1, u2) [f(u1, tj) - f(si,tj)] dg(u1, u2)

i,j t
·

isi+1 itj+1

8i 3 [f(si, u2) - f(si,tj)] dg(u1, u2)

= Ä + I_,²_6,

(2.12)

From (2.1) it follows that

|I^1Ä| = C1f11T,á1,á2110T,â1,â2E i,j

(si+1 - si)^á1+â1(tj+1 - tj)^á2+â2

(2.13)

I²Ä =E

i

Z b1

^,j Xtj)1 (u1, tj) [? g(u1, tj+1) ?g(u1,du1

?u1 ?u1

a1 j

₁si+1 ftj+1

Jsi[f (u1,tj) f (si, tj)]

3

?u1?u2

?²g(u1, u2) du1 du2

t
·

^i,j [f(u1, tj) - f (si,tj)]

[?g(u_?1_u,t₁ j+1) ?g(u1,tj)1 du1

?u1

₁s i +1

C11fkT,á1,á2kgkT,â1,â2MÄ1^{á1+â1+á2+â2-2}.

Next define

f1(u1, u2) = f(u1, u2) - f(si, u2) ifu1 ? [si, si+1).

Then (1.3),(1.4) imply

b1

I1 = C 11g(ui ) 11

fl (U1, -) 11 [a2,b2],á2 [a2 ,b2],â2 du1. (2.14)

a1

Since u1 ? [si, si+1) we have

If1(u1,.)1[a2,b2],á2 = 1f1T,á1,á2 (u1 - si)^á1 = 1f1T,á1,á2 IÄIá1

and

Mg(u1,.)1[a2,b2],â2 = (b1 - a1)â1 kg1T,â1,â2 + 1g(a1, .)1[a2,b2],â2 (2.15)

It follows by replacing in (2.14) that

11I²Ä11 = C111f11T,á1,á211Äll^á1 (11g11T,â1,â2 + 11g(a1,.)11[a2,b2],â2) . (2.16)

Similarly

11I³Ä11 (11g4,â1,â2 + 11g(.,a2)11[a1,b1],â1) . (2.17)

Finally using (2.13),(2.16) and (2.17) in (2.12) we (2.2).

Next we define CT,á1,á2,8 the space _CT,á1,á2 endowed with the norm

1x1T,á1,á2,8 = 1x1T,á1,á2+ sup a1=t1=b1

1x(t1, .)I[a2,b2],á2+ sup a2=t2=b2

kx(.,t2) [a1,b1],á1+1x T,á1,á2.

f (u, v)dg(u, v) f - a1)^â1(b2 - a2)^â2.

~

_.fb1 b2

a

2

The space _{(CT,á1,á2,8,1.1T,á1,á2,8)} is a Banach space.

The convergence of Riemann-Stieltjes sums to the integral for Hölder functions of one variable in shown in [[8],[10],[11]]. The corresponding result for functions of two variables is given in the next theorem.

Theorem 2.1.1. Let T0 = [a1 - å0, b1 + å0] × [a2 - å0, b2 + å0], å0 > 0, and let á1, á2, â1, â2 ? (0, 1] be such that ái + âi > 1. If f ? CT0,á1,á2, g ? CT0,â1,â2, then there exists a unique real number fb2

a

1

a

²

every sequence of partitions Äⁿ = (sⁿ_i ,tⁿ_j ), a1 = s0 < ... < sk(n) = b1, a2 = t0 < ... < tk(_n) = b2, with 1Äⁿ1 ? 0, the Riemann-Stieltjes sums

f(u,v)dg(u,v) such that for

Sog= E i

X(Es^Ti i,s7+1 ] × Et^rj ^i,t7+1]) j

b2

converge to f

f(u,v)dg(u,v). Moreover, the following estimate holds:

a

1

a

2

Proof. It is enough to prove that for every ä > 0 there exist ç > 0 such that for every two partitions (Äi)i=1,2, ai = uⁱ₀ < ... < uim(i) = bi with kÄik < ç we have

~_~~Sf,g

Ä1- _Sf,g ~~~ = ä. (2.19)

Ä-2

Let J ? C⁸(R²) be such that J = 0, J(x) = 0 if 114 = 1 and Iand define

R2

J_å(x) = å^-2J (^x). Consideer the regularizations of f_å, g_å of f,g. Recall that å

f_å(x) =R ₂ J_å(x - y)f (y)dy = f(x - åy)J(y)dy,
and for g_å similarly (as usual f,g are extended as 0 on R² \ T0). It is well
known that f_å ?f, g_å ? g uniformly on T . Also it is easily seen that

(2.20)

få ? CT,á1,á2, g_å ? CT,â1,â2.

Next we show that if 0 < á⁰_i < ái, 0 < â0 i < âi, then

f_å ? f in CT,á⁰ g_å ? g in CT,â⁰

1,á0 2, 1,â0 2,

f_å(a1, .) ? f(a1, .) in C[a2,b2],á⁰₂,

g_å(a1, .) ? g(a1,.) in C[a2,b2],â⁰₂, (2.21)

f_å(., a2) ? f(., a2) in C[a1,b1],á^'₁,

g_å(., a2) ? g(., a2) in C[a1,b1],â⁰₁. (2.22)

We have

(f_å - f) ([s1, t1] × [s², t²])

_Z

= J(u, v) {f ([s1 - åu, t1 - åu] × [s2 - åv, t2 - åv])}

B(0,1)

-f ([s1, t1] × [s2, t2]) dudv,

and then for every å,ä > 0,

sup

si6=ti

|(f_å - f) ([s1,t1] × [s2, t2])|

2

|s1 - t1|^{á0 1}|s2 - t2|^á0

= sup

~ ~|(få - f) ([s1, t1] × [s2, t2])| 2 , |si - ti| > ä, i = 1, 2 |s1 - t1|^á0 1|s2 - t2|^á0

~|(f_å - f) ([s1, t1] × [s2, t2])|

+ sup

₂ , |s1 - t1| > ä or |s2 - t2| > ä

|s1 - t1|^{á0 1}|s2 - t2|^á0

1

= sup {|f(u1, v1) - f(u2, v2)| , |ui - vi| < å, ui, vi ? T0, i = 1, 2}

äá⁰ 1+á0 2

+CkfkT,á1,á2 max(äá1-á0 1, äá2-á0 2) ? 0 as å ? 0, ä ? 0.

Similarly one prove(2.21),(2.22).

Next we choose 0 < á⁰_i < ái, 0 < â0 i < âi with á^'_i + â0 i > 1. Then from (2.20),(2.22) and (2.12) we obtain

~~~~~ + ~~~Sf,g

_~S^f,g

Ä1 - _Sf,g ~~~ = ~~~Sf,g

Ä1 - Sfå,gå Ä2 - _Sfå,gå ~~~

Ä2 Ä1 Ä2

ib1 fa2 b2 b1 _fb2

Qfå_l,gå

"Ä fådgå +Sk2 gå -

faa

1 1

a

2

+

~~

fådgå ~~

lim

å?

H

0

b1 _fb2 b1 _fb2

fådgå =

f dg,

1

1

12

²

1

1

I

~~~~~ + ~~~Sf,g = _~S^f,g

Ä1 - Sfå,gå Ä2 - _Sfå,gå ~~~

Ä1 Ä2

~ n ₁+á⁰ ₂+â⁰ ₂-2

+C ~kfåkT,á⁰ 1,á0 2 + kgåkT,â⁰ (kÄ1k + kÄ2k)á0 1+â0

1,â0 2

_2o

+ (kÄ1k + kÄ2k)á0 ¹ + (kÄ1k + kÄ2k)^á0

~~~~~ + ~~~Sf,g = _~S^f,g

Ä1 - Sfå,gå Ä2 - _Sfå,gå ~~~

Ä1 Ä2

_n

1

+ C1 (kÄ1k + kÄ2k)á0 ₁+â⁰ ₁+á⁰ ₂+â⁰ 2-2 + (kÄ1k + kÄ2k)^á0

+ (MÄ1M + 1Ä21)^á02/ ? 0, as å ? 0 and then IÄiI ? 0. The previous computation also shows that

2.2 Some Additional Properties 23