I.3.2. Ecoulement laminaire et écoulements
turbulent
Un écoulement turbulent peut être
caractérise par une orientation aléatoire (ou fluctuation) des
vecteurs vitesses en chaque point ; autrement dit chaque composante
u(M,
t),
v(M,
t),
w(M,
t), de V(M,
t) Obéissent à des lois de
distributions (au sens probabiliste) en fonction de l'espace et du temps. On
dit que le régime de l'écoulement est turbulent. Un
écoulement turbulent peut posséder une composante moyenne
a (le mouvement global se fait d'ouest en est par
exemple) pouvant dépendre du temps mais de manière plus «
régulière »; les fluctuations ont alors lieu autour de cette
composante moyenne, de sorte que la vitesse s'écrit :
B0@, 3 = ~~~ + D (I.19)
C'est alors Sur v' que l'on fait apparaitre des lois
statistiques.
Dans un écoulement laminaire, le mouvement du
fluide s'effectue en « couches » parallèle entre elles, chaque
couche possédant sa propre vitesse ; le profit de vitesses dans le
fluide en mouvement est biens ordonne. Les vecteurs vitesses conservent une
orientation stable au cours du temps. On dit que le régime de
l'écoulement est laminaire. Lorsque le mouvement laminaire du fluide
dégénère en un écoulement turbulent, il perd son
caractère ordonne et stable ; on dit qu'il y a transition du
régime laminaire vers le régime turbulent, ou plus simplement
transition laminaire turbulent.
La différence entre le régime turbulent et
le régime laminaire peut être représenté par les
courbes donnant la vitesse en fonction du temps en un point M fixe.
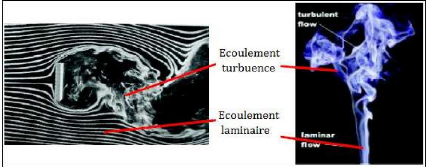
Figure (I.1) : Plaque plane mise à
l'écoulement. [3] Figure (I.2) : Fumée d'une
cigarette.
I.3.3. Ecoulement stationnaire et instationnaire
On dit qu'un écoulement est stationnaire si en
tout point M de Ù, toutes les variables décrivant le mouvement
sont indépendants du temps. Ainsi la pression
P, la vitesse õ, la densité ñ,
l'énergie e d'un écoulement
stationnaire sont des quantités indépendantes du
temps.
I7(m, 3 = I7(m) ?M ? c/ (I.
20)
Tous les phénomènes de propagation
d'onde dans les fluides appartiennent à cette catégorie (onde
à surface d'un liquide, rayonnement d'ondes sonores à partir d'un
jet libre turbulent...), les écoulements atmosphériques sont
aussi essentiellement instationnaires. Les écoulements turbulents sont
aussi par nature instationnaire, cependant on dit qu'un écoulement
turbulent est instationnaire si les variables moyennes sont
indépendantes du temps et si les corrélations d'ordre deux
constituées a partir de ces variables sont invariantes par
transition.
I.3.4. Ecoulement irrotationnel
On dit qu'à un instant t donne,
l'écoulement est irrotationnel dans le domaine D si le rotationnel de la
vitesse V(M, 3 est nul en chacun des points M de D.
ro f, = 0 (I. 21)
Le rotationnel est un vecteur (défini en
cinématique des fluides) qui caractérise en un point M, la
rotation dans l'espace de la particule fluide.
Il s'écrit symboliquement :
.o V(M, 3 = ?~~^V(M, 3 (I. 22)
Il s'écrit par exemple en coordonnées
cartésiennes :
law(M, 3av(M,Trau(M, 3 aw(M,1-- rav(M,
3 au(M, 3].
r;', I7(M, 3 ay az X + az ax Y + ax ay Z (I.
233
| 


