3.1. SPECIFICATION
THEORIQUE (PARADIGME)
Ici, nous allons recourir aux théories
économiques, qui mettent en relation entre le volume de la production,
le facteur Travail et le facteur Capital. Pour établir ladite relation,
nous partirons de l'expression de la fonction de production de Cobb Douglas.
Cette fonction stipule que ; le niveau de la production est
essentiellement expliqué par deux facteurs à savoir Capital
et La main d'oeuvre ou le Travail.
3.2. SPECIFICATION
MATHEMATIQUE
Ici, nous allons schématiser la relation entre la
quantité produit (Q) et le facteur capital et travail est appelé
fonction de production par la formule suivante :
Q = F (K,
L)...............................................................
(1)
Où,
Q : représente le volume de production;
F (K, L) : représente le vecteur du facteur
Capital et Travail ou de la main d'oeuvre.
Ainsi, en supposant une fonction de production du type Cobb -
Douglas, la forme fonctionnelle de la relation ci-haut sera transformée
par l'expression suivante :
Q =
A.Ká.Lâ ..................................................................
(2)
Où,
â= 1 - á
Sous les hypothèses ;
á + â = 1 : le rendement d'échelle
constant.
En somme, pour la fonction de Cobb - Douglas Q =
A.Ká.L â , on aura :
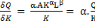 v > 0 ; v > 0 ;
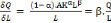 v , avec (â) > 0 ; v , avec (â) > 0 ;
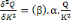 v < 0 ; v < 0 ;
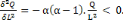
v
Comme cette fonction est non linéaire (Q =
A.Ká.Lâ), pour l'estimer, on doit
la linéariser en faisant une transformation Logarithmique qui conduira
à :
ln(Q) = ln(A) + á ln(K) + â ln(L)
.......................... (3)
q = a + á (k) +
â(l)................................................ (4)
Forme prêt à l'estimation. Ainsi, cette
dernière constitue un modèle de régression multiple de la
relation Production(Q), le facteur Capital(K) et le facteur Travail(L).
3.3. SPECIFICATION
STATISTIQUE
Ici, nous allons introduire le terme d'erreur ou
aléatoire (u) pour montrer qu'il y a d'autres variables qui explique
aussi le volume de la production au sein de l'entreprise GAANA que nous n'avons
pas tenu en compte dans notre modèle.
ln(Q) = ln(A) + á ln(K) + â ln(L) +
ln(ì).......... (5)
q = a + á (k) + â(l) +
ì.................................... (6)
L'ajout du terme d'erreurs, nous conduit au respect des
hypothèses des spécifications économétriques
suivent :
· Hyp1:
Hypothèse de linéarité, c'est-à-dire le
modèle doit être linéaire. Confer l'équation
(6) ;
· Hyp2 E(ìi)=0 :
Hypothèse de Centralité des erreurs, c'est-à-dire
l'erreur possède une distribution dont le centre pour le moment du
premier ordre est zéro ;
· Hyp3 E(ìi
ìj) = 0, avec i 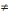 j : Hypothèse de (l'absences d'auto
corrélation), c'est-à-dire les erreurs sont non
corrélée ; j : Hypothèse de (l'absences d'auto
corrélation), c'est-à-dire les erreurs sont non
corrélée ;
· Hyp4 : E(ìi
ìj) =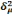 , avec i = j : Hypothèse d'
(Homoscédasticité), C'est à dire la variance doit
être constante et la différence doit être statistique et
significative ; , avec i = j : Hypothèse d'
(Homoscédasticité), C'est à dire la variance doit
être constante et la différence doit être statistique et
significative ;
· Hyp5 E (XU) = 0:
La fonction est de plain rang et les variables
explicatives (le facteur travail et capital) sont non aléatoire. C'est
à dire les erreurs sont indépendantes des variables
explicatives ;
· Hyp6 : Les rangs de la
matrice sont plein ou une fonction de plein rang. C'est-à-dire, les
variables sont linéairement indépendantes.
4. ESTIMATION ET ANALYSE
ECONOMETRIQUE DU MODELE DE PRODUCTION PRISE EN COMPTE DANS NOTRE TRAVAIL
Avec la forme réduite de notre modèle ci
après :
q = a + á (k) + â(l) + ì,
nous allons estimer notre modèle de la production par la méthode
de moindre carré e ordinaire MCO à travers le logiciel
informatique E-VIEWS 3.1.
· Pour créer un fichier sur E-views3.1, on fait
« File - New -
Workfile » ;
· Pour enregistrer les données sur E-views3.1, on
fait « data q k l » ;
· Pour linéariser la fonction sur
E-views3.1 ; cette linéarisation se fait par variable,
c'est-à-dire on doit générer chaque variable :
genr q = log(Q) ;
genr k = log(K) ;
genr l = log(L) ;
· En fin, Pour estimer le modèle par la
méthode de moindre carré ordinaire sur E-views3.1, on fait
« ls q c k l ».
Ainsi, le résultat de l'estimation est
représenté par le tableau output ci-bas :
|
|
Method: Least Squares
|
|
Date: 11/05/10 Time: 09:37
|
|
Sample: 2005:01 2007:12
|
|
Included observations: 36
|
|
Variable
|
|
Coefficient
|
|
Std. Error
|
|
t-Statistic
|
|
Prob.
|
|
C
|
|
2.488887
|
|
0.556928
|
|
4.468960
|
|
0.0001
|
|
K
|
|
0.752022
|
|
0.102584
|
|
7.330801
|
|
0.0000
|
|
L
|
|
0.012452
|
|
0.094916
|
|
0.131192
|
|
0.8964
|
|
R-squared
|
|
0.923978
|
Mean dependent var
|
12.11191
|
|
Adjusted R-squared
|
|
0.919371
|
S.D. dependent var
|
0.281610
|
|
S.E. of regression
|
|
0.079964
|
Akaike info criterion
|
-2.134827
|
|
Sum squared resid
|
|
0.211010
|
Schwarz criterion
|
-2.002867
|
|
Log likelihood
|
|
41.42688
|
F-statistic
|
200.5424
|
|
Durbin-Watson stat
|
|
2.117370
|
Prob(F-statistic)
|
0.000000
|
Estimation Command:
=====================
LS Q K L C
Estimation Equation:
=====================
Q = C(1)*K + C(2)*L + C(3)
Substituted Coefficients:
=====================
Q = 0.7520220214*K + 0.01245218676*L +
2.488886739
5. VALIDATIONS ECONOMETRIQUES DE
L'ESTIMATION
| 


