III.2. MODELISATION DU
REGULATEUR DE VITESSE
Dans la modélisation des régulateurs de
centrales hydroélectriques, l'entrée du régulateur de
vitesse est l'erreur de vitesse et la sortie de celui-ci est la position des
directrices dans le cas de la turbine Francis bien entendu.
III.2.1. Régulateur
accélérotachymétrique mécanique.
Lorsqu'un groupe fonctionne couplé à un
réseau important, il n'y a pas de question grave de stabilité
hydraulique, puisque sa vitesse est maintenue par le couple synchronisant
exercé par les autres groupes ; mais il faut que son
régulateur soit assez rapide pour que le groupe obéisse
suffisamment vite à une demande d'augmentation ou de diminution de la
charge.
Par contre, lorsque le même groupe sera appelé
à fonctionner seul sur le réseau, il faudra que son
régulateur ajuste sa vitesse à la valeur normale, à la
suite d'une accélération produite par une variation de charge,
assez rapidement pour éviter de trop grandes variation de
fréquences.
L'autoréglage facilite cette opération, mais
l'inertie hydraulique de l'eau s'y oppose et empêche de réaliser
un réglage à la fois stable et infiniment rapide sur le
réseau autonome.
Une caractéristique d'un régulateur est donc sa
promptitude de réglage, qui peut être définie
comme l'inverse de la constante de temps ô du mouvement de vannage,
supposé d'allure exponentielle ; M. Stein a proposé de
donner à cette constante ô le nom de « lenteur de
réglage ».
Le régulateur
accélérotachymétrique est soumis à la fois à
une action proportionnelle à l'écart de fréquence Äf
et à une action proportionnelle à l'accélération
soit  , où le coefficient de proportion m représentant le temps
en secondes nécessaire à l'accélération mis en jeu
de produire un écart de vitesse fournissant le même effort dans le
régleur que l'accélération considérée. Cette
constante est appelé dosage
accélérotachymétrique.
Bien que le régulateur puisse fonctionner sans
asservissement, on lui confère toujours un certain statisme permanent
ó, généralement assez petit de l'ordre de 3 à 4
%.
Ainsi, l'équation du mouvement du régulateur
accélérotachymétrique est donnée par les
expressions suivantes :
 (17)
Dont la première équation de ce système
donne le modèle de la chaîne directe et le second le modèle
de chaîne de contre-réaction négative.
L'application de la transformation de Laplace au
système d'équation donne :
 
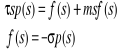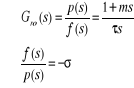
Ainsi, le diagramme fonctionnel du régulateur
accélérotachymétrique est donné par le
schéma de la figure ci-dessous.
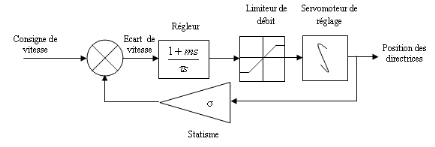
Figure III.6. Diagramme fonctionnel du régulateur
accélérométrique.
Ainsi la fonction de transfert du régulateur en
bouclé fermée ou du régulateur avec asservissement est
donc donnée par l'équation suivante :
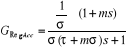
Calcul des paramètres du régulateur
Considérons le système d'équations
différentielles du modèle de la surpression dans les conduites
forcées, de la masse tournante et du régulateur
ci-dessous :
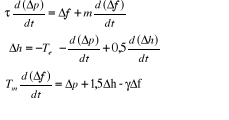
En appliquant la transformation de Laplace à ce
système d'équations, on a :
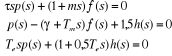
En annulant le déterminant des coefficients des
variables p(s), f(s) et h(s), on a :
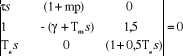
Ou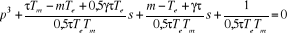 
En appliquant le critère de stabilité de ROUTH
à l'équation caractéristique ci-haut trouvée et en
identifiant que :
 ,  et 
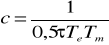
On a :
s3
s²
s1
s0
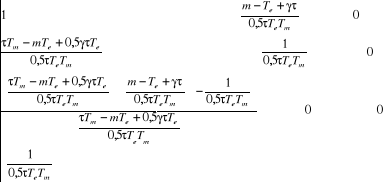
Pour que le système soit stable, il faut que les
éléments de la première ligne soient tous
supérieurs à zéro.
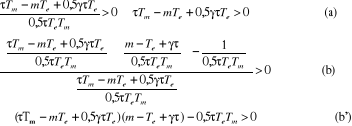
Pour trouver les paramètres du régulateur, il
sied de faire une discussion sur les conditions de stabilité
ci-dessus.
Discussion du fonctionnement :
Sans autoréglage
Si on considère ã = 0, les conditions de
stabilité du critère de ROUTH deviennent :
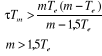
Ce qui veut dire que :
1°) le dosage accélérométrique m
doit être au moins égal à 1,5Te.
2°) le produit des constantes de temps du groupe et du
générateur doit avoir une certaine valeur minimum.
3°) cette valeur minimum est elle-même susceptible
de passer par un minimum pour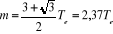 
4°) si on donne à m cette valeur optimum, on
trouve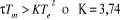 
Les conditions de stabilité de ROUTH
énoncées dans ce cas précis sont appelées
critère fondamental établi par D. Garden.
Influence de l'autoréglage.
Les relations (a) et (b') peuvent se mettre sous la
forme :
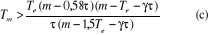
Cela entraîne comme condition préalable 
La valeur qui donne le minimum du second membre de la relation
( c) et celle qui annule sa dérivée première,
soit :
 (e)
A condition que sa dérivée seconde soit
positive, ce qui exige :
 (f)
En nous basant sur les relations (c), (d), (e) et (f), on peut
déduire les paramètres du régulateur :
 Et en remplaçant cette expression dans la relation (e), on
trouve l'expression du dosage accélérométrique en fonction
de la constante d'inertie hydraulique :
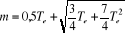
Les valeurs numériques de m et ô
respectivement dosage accélérométrique et lenteur
de réglage sont données par :
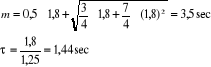
La fonction de transfert du régulateur est donc
donnée par sa forme numérique :
| 
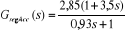
