Memoire Online - Contrainte Psycho-Physiques et Electrophysiologiques sur le codage de la stimulation électrique chez les sujets porteurs d'un implant cochléaire

Cet article décrit les caractéristiques de la stimulation électrique du modulus cochléaire générée par l'implant cochléaire Digisonic^®.

Dans cet article nous avons modélisé la stimulation électrique générée par l'implant cochléaire en fonction de divers paramètres. Les contraintes physiologiques de la stimulation électrique sont décrites : équilibre des phases, charges par cycle faibles, stimulation localisée ... La description et la simulation de la stimulation par l'implant cochléaire Digisonic^® permettent de conclure à une grande sécurité :

Modelling of the electrical stimulation delivered by the
DIGISONIC Multichannel cochlear implant.

The study concerns a model of the skin recording given by the DIGISONIC pulses. Digisonic is a multichannel cochlear implant made by the French society MXM. Two models (using 3 and 5 electrodes) are described, one simple, the other more complex. Results show that both models behaved very similarly when the pulse duration was between 5 and 160 its (range commonly used with cochlear implantees). This duration was Little affected by the physiological medium impedance. The stimulation concerning the medium influence and the _.pulse duration, led to information about the delivered electric load and the stimulation shapes. This modelling is developped in order to help the setting of electrode thresholds with implantees.

A cochlear implant (CI) is a device which restores some auditory sensation to people having a
total bilateral cophosis. CI delivers an electrical stimulation to the auditory nerve. Speech
^--recognition performances of some patients are really amazing (some of them can even speak on

the telephone). Nevertheless, clinical results are very heterogeneous. Some factors such as aetiology of deafness, length of sensory deprivation, etc can explain implantees' performances, but much of the results still remains unexplained.

In spite of the importance of knowing the stimulated zone on the cochlea, only a few studies have considered the influence of the physical situation of the electrical stimulation (Black et al, 1983; O'Leary et ai, 1985). This information is important, as it concerns the fondamental of the voice frequency (pitch). It has been shown that modifications occur when acoustical frequencies are redistributed along the electrodes because the sensation varies with, the stimulated zone (Shannon, 1983). Moreover, some authors have shown that the tonal perception, regarding the electrode, is linked to the diffusion width of the current (Townshend et al, 1987). The possibility of pinpointing the stimulation could help to estimate the frequency gap perceived between two electrodes taking into consideration the tonotopic difference.

The necessity of using a coupling condenser between the patient and his cochlear implant in order to prevent the electrolysis of the biological medium, adds fiwther problems. Condenser addition introduces artefacts in the circulation of current charges for short duration pulses (due to non-linearity). Consequently, this fact can modify the conversion of acoustical dB to electrical dB. Moreover, it is necessary to keep the charge delivered to the cochlea under control, in order to remain below the safety limit which is 40 itC per square millimetre and per stimulation cycle (Frayel et al, 1986).

The goal of this study is to built up a model of the electrical recording observed with a pulse delivered between the implant electrodes. lis link with the assessment of the correct working order of the machine justifies the analytical study to establish the influence of electrode and medium parameters. First, we will study the principle of the electrical stimulation given by the DIGISONIC cochlear implant. Two models with increasing complexity (3 and 5 electrodes) were constructed. Then the responses of the two models were compared. Relation between the

pulse duration and the amount of electricity (charge) delivered bythe implant, was calculated for several impedances of the physiological medium.

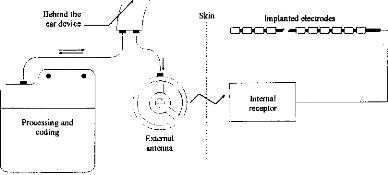
Figure 1: Block Diagram of the MXM DIGISONIC cochlear implant. The external part is on the left and the implanted part on the right.

The DIGISONIC is a cochlear implant made of two different parts (fig 1); the external one .performs the signal processing (real time FFT) and transmits some information to the second part. The internai part, totally implanted, is made of 15 active electrodes distributed along the cochlea (Beliaeff et al, 1994), usually situated from 5 to 20 millimetres from the round window. The distance between two electrodes is 0.7 mm. A frequency band is attached to each electrode. The stimulation used is common ground (one electrode is active, and ail the others are connected to the ground). Each electrode has a 220 nF serial condenser to force the charge mean value to zero. The generator can deliver pulses with variable amplitude and duration. Ordinarily, for a given patient, the amplitude is fixed (ranging from 1.2 to 6 volts, where 3.35V is usually taken). The duration of the pulse is variable; it transmits the volume. Generally the

duration lasts from 20 to 60 ils; the maximum range is from 5 to 310 ris. The output
impedance of the stimulation transistor cannot be neglected; it is connected to the output

In our models, the cochlear implant is represented by a generator of pulses connected in series with a condenser (C2=220nF). As indicated above, the output impedance of the generator, R(E), is variable. The electrode and physiological medium were represented by a condenser placed in parallel with a pure resistance (Rattay, 1990). In vitro measurements, performed at the MXM laboratories, indicated that the capacity between two electrodes is about 100 nF (C1) and the resistance is 2 kohms (R1). 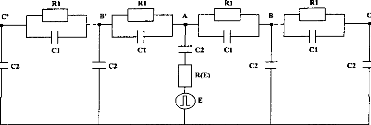Modelling of the electrical stimulation of the cochlear implant in a physiological medium, is represented by the circuit indicated on figure 2.

Fig 2: Model of the stimulation delivered by the cochlear implant DIGISONIC. The generator is between point A (active electrode) and the ground; ail 14 other electrodes are connected the ground through condensers. E varies from 1.2 to 6 volts, and the pulse duration is from 5 10 310 ,us. C2 is 220 nF and R(E) is a fonction of E. Concerning the physiological medium, RI is 2 kohms and C1 is 100 nF (average values).

A full model would consider a 14th order differential equation with one for each electrode. But
the further we are from the active electrode, the weaker the current. Aller several electrical

divisions the current can be neglected. One of the aims of our modelling was to reduce the number of useful electrodes. We considered 3 electrodes A, B, B' (3-pole) in the first model and five electrodes A, B, B', C, C' (5-pole) in the second model. Consequently 13 active electrodes were possible in the first model (1 electrode had to be taken on each side of the active electrode) and eleven in the second model. In order to simplify the models, symmetrical representations (on each side of the active electrode) were used, thus leading to a simpler calculation. Then, three time constants were introduced, TI=R1C1, T2=R2C2, T3=R3C3. The Laplace transformer was used in the calculation. Finally, V1 and V2 were determined by the following equations (alter the classical simplifications).

E - (16r ₂r² +8r r 2r 3) p³ +(20r² +32r r 2+8r 2r ₃+20r r ₃+ 421) P² + (40r + 16r 2+20r 3) P +20

In order to solve the above differential equations, they were rewritten in their differential format.

Then higher order equations were written as first orders with variables being double or triple integrals of voltages V1 or V2. The solution was then achieved with the Runge-Kutta method, using variable steps.

First, the evolution of R(E) was directly measured on an implant. Figure 3 shows the evolution on two different charge impedances (1 kohm and 10 kohms) when E is increased. R(E) decreases exponentially, with respect to E. An asymptotic value (500 ohms) was observed. When E=3.35V (voltage currently used) is used, then R(E) is close to 1 kohm.

2000

C
O

1500

E
o

1000

"FI

C
o

Figure 3 : Impedance of the output transistor with respect to the output voltage when the load is 1 kohm (full dots) and 10 kohms (empty squares).

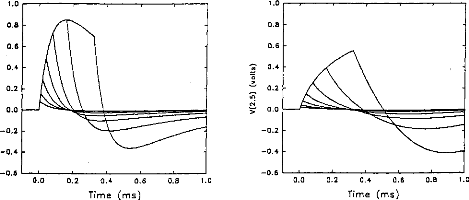
The next step was to compare the two models when the pulse duration varied. The experimental range was from 5 to 320 gs and the steps were exponentially increased. Figure 4 indicates the voltage VI given by the first model. Figures Sa and 5b show the simulation of VI and V2 by the second model. VI (V(1,3) and V(1,5)) are very similar for the two models. V2 is mostly lower than VI when the duration of the excitation pulse is below 80 gs.

1.0 0.8 0.6 0.4 0.2 0.0 -0.2 -0.4 -0.6

Figure 4: V(1, 3) obtained from the 3-pole model, with the pulse duration (t=5, 10, 20, 40, 80, 160, 320 ,us) taken as a parameter. The load had the physiological value of 2 kohms and Cl was 100 nF (E=3.35 volts, R(E)= lkohm). The curve on the right refers to 320 ,us.

mode!) with respect to the pulse duration (1=5, 10, 20, 40, 80, 160, 320 us). The load had a physiological value of 2 kohms and Cl was 100 nF (E=3.35 volts, R(E)= lkohm).

Figure 5b: V(2,5), VB-VC, simulation (5- pole model) with respect to the pulse duration (1=5, 10, 20, 40, 80, 160, 320 ,us). The load had a physiological value of 2 kohms and Cl was 100 tiF (E=3.35 volts, R(E)= lkohm)

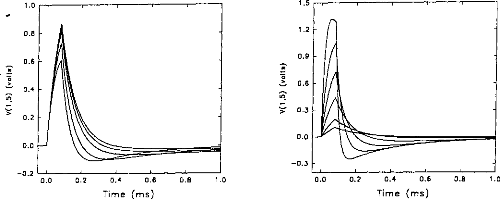
In normal conditions, the impedance of the physiological medium does not vary significantly. But, in special circumstances, for instance in the case of partially ossified cochlea, impedance is increased on some electrodes. Figures 6a and 6b show the evolution of the impulsion voltage (using the second model) respectively considering the resistance R1 and the capacity C l. The

duration of the excitation pulse was kept below 80 lis. Variation of the response (shape and amplitude) was high with respect to C I (figure 7). On the contrary, the influence of RI was rather small. The time to reach the maximum of the output pulse followed the value of R1.

Figure 6a: V(1,5) simulation (5-pole model), Figure 6h: V(I,5) simulation (5-pole mode!),

with respect to the load resistance (RI = 1, 2, when the condenser had the following values^.

5,
· 10, 20 kohms) where Cl = 100nF. (E=3.35 (CI =20, 50, 100, 200, 500, 1000 nj9 where

volts, R(E)= I kohm). The higher the RI=2kohms. (E=3.35 volts, R(E) = I kohrn).

impedance, the greater the amplitude. The smaller the CI, the higher the amplitude.

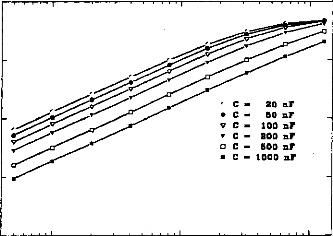
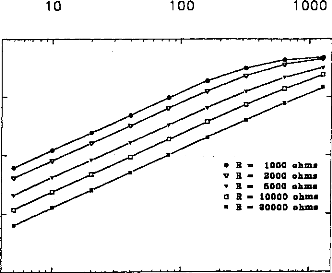
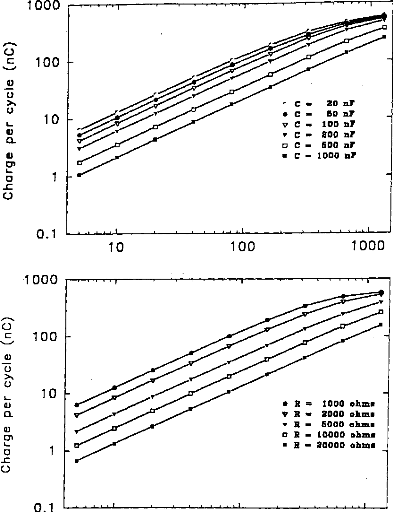
It is possible to calculate the electrical charge delivered to the medium taking the integration of the positive part of the pulse and a division by Rl.

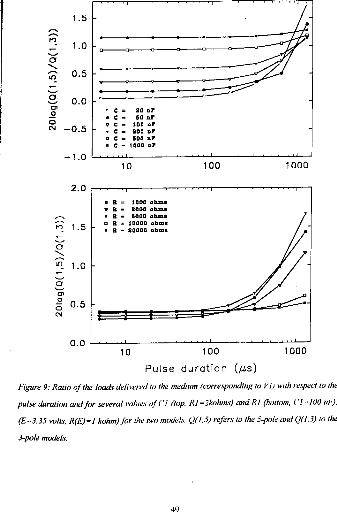
The amount of electricity denoted Q, has been calculated in different situations, where the excitation pulse duration and the medium impedance varied. Results are given in figures 7 (first model) and 8 (second model). Results show that Q was linearly increased until an excitation duration of 160 jis caused saturation. The same trend was observed with respect to the

medium resistance. Both models led to equivalent results for pulses shorter than 320 las and with a capacity C2 less than 500 nF (Q2/Q1<ldB) (figure 9).

Figure 7: Load delivered hy the electrodes B and B' calculated using the 3-pole model, with respect 10 the pulse duration when several values qf CI (top, R1=2 kohms), or RI (bottom, Cl - 100 nF) are used (E=3.35 volts, R(E) =1 kohm)_:

Figure .8: Load delivered hy the electrodes B and B' calculated using the 5-pole model, with respect to the pulse duration when several values of Cl (top, R1=2 kohms), or RI (bottom, C1=100 nF) are used (E=3.35 volts, R(E) = 1 kohm).

Figure 9: Ratio of the loach delivered 10 the medium (corresponding to VI) with respect to the pulse duration and for several values of CI (top, RI =2kohms) and RI (bottom, (' I 100 id), (E=3.35 volts, R(E) = I kohm) for the two models. Q(1, S) refers to the 5-pole and 0(1,3)10 the 3-pole models.

	2.0
ri^,	1.5
1.11	1.0
rn
0	0.5
	0.0

The comparison of the results given by the two models showed a high similitude for the shape and values of the charges delivered by the DIGISONIC DX10 cochlear implant when the excitation pulse was shorter than 320 gs. When the decimal logarithm was equal to 1, the ratio of charges was 1.12, which is practically equivalent to 1. This could mean that the excitation path is very short and does not spread throughout the electrodes. Consequently, a 3-pole circuit appears adequate to provide a good model of the stimulation. At least, a 5-pole model did not lead to different results. A special non-symmetrical model needs to be established for the side electrodes (1 and 15).

The shape of the response was significantly influenced by the impedance of the physiological medium between two electrodes. In this case, it seemed that information about the status of the active electrode couid only be obtained by considering the surface potentials in cochlear implantees (Mens et al, 1994; Gallégo et al, 1997). Surface potentials were potential differences recorded between surface electrodes situated on the skin. They were produced by the electrical action of the implant electrodes. They couid be interpreted by the action of a stimulation dipole situated on the line connecting the recording electrodes.

One application could be to help set the liminar and comfort thresholds on each electrode. The more ossified the cochlea, the higher the impedance. Consequently, in the case of ossification, an increase of the liminar thresholds and a reduction of the electrical dynamic couid be seen. If we consider figure 6a, it can be seen that the offset time, from the peak to the baseline, is a function of the impedance, which consequently could be evaluated.

If the line connecting the two skin electrodes, E 1 and E2 is orthogonal to the dipole, the action of the dipole is the same on El and E2. Consequently the potential difference is null. In all other cases, this potential difference is not equal to zero (fig 10).

Figure 10 : Schematic representation of the skin electrodes relative to an exciting dipole.

Figure 11 shows a typical surface potential. Waveform is modified by the bandpass of an analog filter on the recording system (10-3000 Hz).

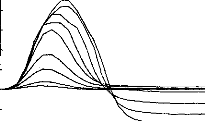
Figure 11: Surface potentials VE1-VE2 recorded on a cochlear implant subject with regard to pulse duration (1=5, 9, 22, 34, 60, 86, 137, 188, 239 ps).

0 0 0.1 0.2 0.3 0.4 0.5 0.6

Time (ms)

0.7 0.8 0.9 1 0

The amount of charge delivered by the implant grew linearly with the duration of the pulse. It has been shown (Shannon, 1992) that an increase in perceived volume is proportional to the electrical charge delivered to the medium between two electrodes. It has also been established, with normal hearing people, that the perceived volume is in proportion to the acoustic stimulation given in decibels. In other words, the stimulation growth should be proportional to the duration of the pulse. Following these considerations a logarithmic compression of the acoustical pressure could be converted to a pulse duration. The introduction of condensers did

not increase the difficulty of evaluating the charge delivered by the electrodes. The maximum

charge delivered by an electrode is, according to figures 7 &8, less than 1 giC. The surface of the electrode is about one square millimetre, and the charge density in the tissue is less than 1 itC/mm². These charges remain well below the safety limit established in order to assure the integrity of the physiological tissues (40iic per square millimetre and per cycle).

Considering the remote action (on the skin) of electrical stimulation seen so far, this model may be considered as a first step toward a more complete one. The next step in this modelling would be to extend the models to 'in vitro' and 'in vivo' situations (figure 10), with corresponding measurements. This would help the localisation of the stimulation on the cochlea, the assessment of the quality of the implanted device and the measurement of the electrode impedances.

In our model, the system was even more complicated by the fact that two dipoles must be considered when the stimulation is symmetrical (in the 3-pole or the 5-pole representation). This situation will be considered in a further step of the modelling.

The present study shows that a 3-pole model provides an adequate means of representing the electrical stimulation delivered by a cochlear implant used in a common ground mode. The extension to a 5-pole model did not really change the results.

The influence of the medium resistance modified the shape of the stimulation. Consequently, the knowledge of the impulse response indicates the status of the medium, mostly in the case of ossification. The recording of the electrical response produced by a pulse indicates also the amount of electricity delivered between two electrodes. The relation is non linear and the shape has to be seen to evaluate the magnitude of the stimulation.

The next step would be to use this 3-pole model in order to simulate the surface potentials on
the skin. The relation between the prediction and the observed values will determine the power

of the model, model which is of the utmost importance to establish the cochlear implant working mode and the status of the physiological medium surrounding the electrodes.

The authors acknowledge the people and institutions supporting their work: the MXM society, the Hospices Civils of Lyon, the CNRS, the University of Lyon and Professor Lionel Collet Director of the laboratory.

- Beliaeff M., Dubus P., Leveau J.M., Repetto J.C., Vincent P. Sound Processing and Stimulation coding of DIGISONIC DX10 15-channel Cochlear Implant. Advances in cochlear implant, Ed. IN Hochmair (Innsbruck). 1994;198-203.

- Black R, Clark G, Tong Y, Patrick J. Current distributions in cochlear stimulation. Ann NY Acad Sci, 1983, 405, 137-145.

- Fravel R. Cochlear implant electronics made simple. Otolaryngol Clin North Am, 1986, 19, 11-22.

- Gallégo S, Truy E, Morgon A, Collet L. EABRs and surface potentials with a transcutaneous

multielectrode cochlear implant. Acta Otolaryngol (Stockh), 1997, 117 (in press).

· - Mens LHM, Oostendorp T, Broek P van den. Identification Electrode Failures with Cochlear

- Townshend B, Cotter N, Van Compernolle D, White R. Pitch perception by cochlear implant subjects. J Acoust Soc Am, 1987, 82, 106-115.

Contrainte Psycho-Physiques et Electrophysiologiques sur le codage de la stimulation électrique chez les sujets porteurs d'un implant cochléaire

Article 2 :

MODELLING OF THE ELECTRICAL STIMULATION DELIVERED BY THE
DIGISONIC MULTICHANNEL COCHLEAR IMPLANT
S. Gallégo, B.L. Luu, C. Berger-Vachon
Advance in Modelling & Analysis, 1998 39: 1, 39-53

Contrainte Psycho-Physiques et Electrophysiologiques sur le codage de la stimulation électrique chez les sujets porteurs d'un implant cochléaire

Article 2 :

MODELLING OF THE ELECTRICAL STIMULATION DELIVERED BY THEDIGISONIC MULTICHANNEL COCHLEAR IMPLANTS. Gallégo, B.L. Luu, C. Berger-VachonAdvance in Modelling & Analysis, 1998 39: 1, 39-53

MODELLING OF THE ELECTRICAL STIMULATION DELIVERED BY THE
DIGISONIC MULTICHANNEL COCHLEAR IMPLANT
S. Gallégo, B.L. Luu, C. Berger-Vachon
Advance in Modelling & Analysis, 1998 39: 1, 39-53