Conception d'antenne radiofréquence dédiée à l'imagerie par résonance magnétique

2.3.2 Principaux paramètres de Caractérisation d'antennes RF

2.3.2.1 Fréquence de résonance

Le signal RMN provenant de l'échantillon étant extrêmement faible, il est alors nécessaire d'utiliser des antennes de détection résonante, dont la fréquence de résonance est ajustée à la fréquence du signal RMN (fréquence de Larmor). La résonance de l'antenne se traduit par une sélectivité fréquentielle et permet donc de filtrer une partie du bruit associé à la détection du signal. Une antenne IRM peut-être représentée classiquement par un circuit RLC. (Fig.2.6). R est la somme de toutes les résistances pouvant être associé au mécanisme de perte au sein des conducteurs et au sein de l'échantillon. En particulier,

R = Rbobine + Rchantillon (2.6)

Rbobine Prend en compte les pertes au sein du conducteurs de la bobine du récepteur et dépend de la géométrie du conducteur; _Rchantillon correspond aux pertes causés par les courants RF induits par la fluctuation du champ magnétique et du champ électrique dans l'échantillon, principalement générée par les condensateurs. L est l'inductance du système tenant compte de l'énergie qui peut être stockée dans le champ magnétique, et est liée à la géométrie et la taille du conducteur; C la capacité du système résultant principalement de la contribution de condensateur discret; I est le courant qui circule dans la bobine. En appliquant la loi de Kirchhoff, la fréquence de résonance du circuit correspondant à la fréquence pour laquelle le courant est maximal, peut être calculée comme suit :

1

f_o = v (2.7)

2ð LC

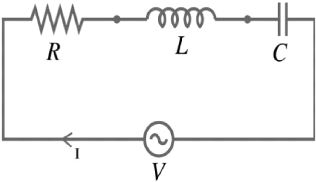
FIGURE 2.6 - circuit RLC équivalent d'une antenne radio-fréquence [25]

2.3. LES ANTENNES RADIOFRÉQUENCES 25

2.3.2.2 Facteur de qualité de l'antenne

Le facteur de qualité Q d'une antenne RF en réception peut être traduit par son aptitude à transmettre le signal à la fréquence de résonance tout en atténuant le bruit aux autres fréquences. Il peut être défini comme le rapport de la fréquence de résonance f_o à la largeur de la bande passante Äf autour de la résonance :

fo f_o

Q = = (2.8)

f1 - f2 Äf

où f1 et f2 sont les deux fréquences de coupure à -3dB. Äf correspond ainsi à la bande passante à -3dB de l'antenne. Pour une antenne ayant un facteur de qualité élevé, sa bande passante est étroite et il est donc important d'accorder le plus précisément possible la fréquence de résonance de l'antenne à la fréquence de Larmor des spin. Le facteur de qualité peut également être abordé d'un point de vue énergétique au travers de l'expression ci-dessous :

Energie.totale.stockee.par.l^'antenne

Q = 2ð (2.9)
Energie.dissipee.par.cycle

- L'énergie stockée par l'antenne correspond à l'énergie magnétique emmagasinée dans l'in-ductance de l'antenne (¹2 Li², avec i le courant parcourant l'antenne).

- L'énergie dissipée par cycle correspond à l'énergie dissipée dans la résistance équivalente de l'antenne (¹2 Ri², normalisée par la fréquence de résonance)

Le facteur de qualité Q est alors relié aux paramètres électriques équivalents du circuit par :

/

Lw_o 2ðf0L 1 L

Q = R = R = (2.10)

R C

Avec w_o, la pulsation de résonance de l'antenne. Une mesure de la performance de l'antenne est le rapport r entre le facteur Q d'une bobine non chargée et le Q d'une bobine chargée :

r =

Qnon charg Qcharg

Rbobine + Rchantillon = (2.11) Rbobine

Mémoire de Master of science de Physique, par Severin Didjeu. UYI

2.3. LES ANTENNES RADIOFRÉQUENCES 26

Où _Rbobine est la résistance de la bobine et _Rchantillon est la résistance induite par l'échan-tillon. L'indice r devrait être maximisé pour fournir un RSB/SNR maximal en IRM, puisque

/

1 - 1

SNRá r