CHAPITRE III
RÉSULTATS DE SIMULATIONS ET
DISCUSSIONS
42
3.1 Introduction
L'analyse théorique impliquée dans la conception
de quelques types d'antennes, est devenue très complexe, et dans
beaucoup de cas une solution exacte est impossible. Des logiciels de
simulations ont donc facilité l'analyse des problèmes et la
conception des structures de plus en plus complexes. Dans ce chapitre, nous
décrivons l'environnement de simulation que nous avons utilisé,
nous présentons également les résultats de simulation de
notre antenne qui sont évalués par la simulation du champ
magnétique B dans le plan (sensibilité) et dans l'espace. Ces
simulations sont réalisées avec le logiciel MATLAB version R2018b
(9.5.0.944444) installé dans un ordinateur personnel de
caractéristiques 64 bits, 3 GB de RAM, 2.16 GHz.
3.2 Présentation de l'outil de simulation :
logiciel Mat-lab
MATLAB signifie Matrix laboratory. C'est un logiciel
distribué par la société Math-Works qui fournit
principalement des moteurs de calcul numériques, et une interface de
programmation simple. Il est distribué avec un grand nombre d'options,
appelées Toolbox. Sans option, MATLAB n'est pas capable de proposer des
résultats de calcul formel, et permet principalement de résoudre
des problèmes matriciels, c'est à dire linéaires (fig
3.1).
3.3. RÉSULTATS DE SIMULATIONS 43
FIGURE 3.1 - interface MATLAB
3.3 Résultats de simulations 3.3.1 Approche analytique
Pour la bobine de surface boucle circulaire, le champ
magnétique par unité de courant B/I (sensibilité) a
été calculé analytiquement (eq 2.55) à la
fréquence de 64 MHz le long de l'axe (oz), de part et d'autre du maximum
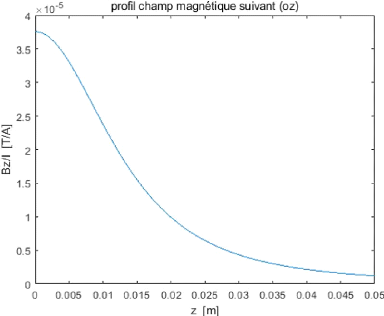
en z=0 qui correspond au centre de la bobine. La figure 3.2 montre le
tracé (le long de l'axe des z) du profil champ magnétique par
unité de courant (sensibilité) en fonction de la profondeur
variant de 0 à 50 mm pour une Boucle circulaire de 20 cm de
diamètre. En règle générale, pour avoir un bon SNR
dans la ROI, le rayon de l'antenne doit correspondre à peu près
à la profondeur d'un échantillon à l'étude.
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
3.3. RÉSULTATS DE SIMULATIONS 44
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
FIGURE 3.2 - Profil champ magnétique par unité
de courant en fonction de la profondeur z pour la boucle circulaire
La rapide décroissance en z est caractéristique
de cette antenne qui présente une forte sensibilité mais à
une distance réduite, à l'inverse des antennes volumiques comme
ceux à base de solénoïde. L'allure des sensibilités
des géométries circulaire et carrée sont relativement
similaires.
3.3.2 Approche numérique
Pour obtenir la variation spatiale du champ magnétique
sur des profils moins élémentaires tels que des plans ou
même un volume, une formulation analytique simple n'est plus possible.
Une intégration numérique de Biot-savart est donc
nécessaire. Le résultat du calcul numérique sur MATLAB
concernant le champ magnétique dans le plan (xoy) pour l'an-tenne de
surface à boucle circulaire est illustré à la figure 3.3;
Le champ magnétique B généré pendant la phase de
transmission pour la même antenne a également été
calculé à la fréquence de 64 MHz dans un plan orthogonal
au plan de la bobine traversant son centre. Le profil de champ
magnétique extrapolé à partir de l'antenne et sa
représentation dans le plan (2D) sont représentés sur les
figures suivantes :
3.3. RÉSULTATS DE SIMULATIONS 45
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
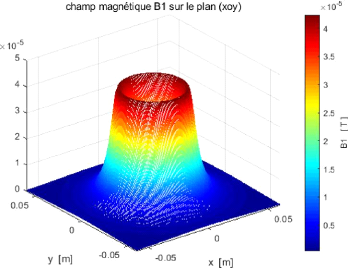
FIGURE 3.3 - Profil du champ magnétique B pour une
antenne de surface simple boucle circulaire

FIGURE 3.4 - représentation dans le plan (2D) du champ
magnétique
3.4. DISCUSSION 46
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
Comme on pouvait s'y attendre, le champ est très
homogène près du plan de stock de la bobine et son amplitude
décroît rapidement au fur et à mesure qu'il
s'éloigne de ce plan. Cela est très évident si on observe
la ligne de profil suivant l'axe oz passant par le centre de la bobine comme
vue à la figure 3.2.
La figure 3.3 est le tracée du champ magnétique
en tout point de l'espace; plus on s'éloigne du centre de la bobine,
plus le champ magnétique devient intense en surface; cela est visible
par des couleurs allant de la bleu (au centre) jusqu'à la rouge (en
surface). La bobine transporte des courants électriques dans la
même direction pour améliorer la sensibilité du champ au
centre de l'antenne; le champ magnétique auquel on associe une pulsation
très homogène et non nul au centre l'antenne.
L'amélioration de la sensibilité permet alors d'obtenir un RSB
beaucoup plus élevé à la surface de l'échantillon
grâce à un meilleur couplage magnétique local et un
filtrage spatial du bruit provenant de l'échantillon.
La figure 3.4 est la représentation dans le plan (2D)
du champ magnétique le long d'un cylindre avec un courant I
distribué à la surface du cylindre.
Le tableau 3.1 indique les paramètres de boucle
évalués à une fréquence de 64 MHz pour une boucle
circulaire dont les dimensions satisfont au rayon de la boucle 20 cm. Cette
fréquence correspond à la fréquence du proton dans un
scanner IRM de 1,5 T. La résistance de la bobine a été
calculée avec équation (2.18) pour la boucle circulaire en
considérant un rayon de fil de 2 mm pour cette boucle, tandis que la
résistance induite dans l'échantillon a été
estimée en utilisant l'équation (2.21). Les dimensions de cette
antenne ont été calculées pour avoir un champ
électromagnétique uniforme.
TABLE 3.1 - Estimation des paramètres
à 64 MHz
|
bobine
|
Rbobine(mÙ)
|
Rchantillon(mÙ)
|
L(mH)
|
r
|
|
diamètre de la boucle circulaire 20 cm
|
53.9
|
51.01
|
52.5
|
1.95
|
3.4 Discussion
Le calcul du champ magnétique décrit dans cet
article est basé sur l'équation de Biot-Savart. Cette
théorie peut être employée pour l'analyse et la conception
de bobines dont la taille est une petite fraction de longueur d'onde. Par
exemple à 64 MHz, la longueur d'onde associée est de 4,7 m et
l'hypothèse quasi statique est valable pour toutes les dimensions de la
bobine. En augmentant l'intensité du champ magnétique,
l'approximation est la même que lorsque la dimension de l'antenne
diminue. La géométrie circulaire est la conception la plus simple
pour une bobine à surface unique. Cependant, une bobine
constituée par une boucle de géométrie différente
pourrait être nécessaire lorsque des champs de vision (FOV) sont
souhaités. En particulier, les formes rectangulaires et elliptiques
pourraient être préférées lorsqu'une zone doit
être imagée, mais à condition de faire intervenir la
profondeur
3.4. DISCUSSION 47
Mémoire de Master of science de Physique, par Severin
Didjeu. UYI
de pénétration. Dans les cas où la bobine
et l'échantillon ont des formes géométriques
différentes, les antennes de surfaces sont incurvées autour des
anatomies, la littérature propose l'application des méthodes
numériques pour la conception et la simulation des antennes, qui
tiennent compte du rendement de l'antenne, même à fort champs
magnétiques.
48
| 


