Conception d'antenne radiofréquence dédiée à l'imagerie par résonance magnétique

2.4.1 Géométrie et matériaux

L'antenne de surface a une forme circulaire avec un diamètre de 20 cm. Le conducteur est un fil cylindrique de rayon a=2mm. La définition de la géométrie est planifiée, ce qui a été réalisé en utilisant une structure circulaire à laquelle deux petites parties ont été enlevées pour permettre d'insérer le condensateur d'accord et la source (fig 2.9).

Mémoire de Master of science de Physique, par Severin Didjeu. UYI

2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE ANTENNE

SIMPLE BOUCLE CIRCULAIRE 30

FIGURE 2.9 - géométrie de l'antenne de surface

2.4.2 Eléments de circuit et réglage de la bobine

* Calcul de la résistance de la bobine pour une boucle circulaire

La résistance de la bobine peut être estimée en utilisant la formule classique

Rbobine = ñl (2.16)

S

Qui prend en compte la géométrie du fil conducteur, où l et S sont respectivement la longueur totale du conducteur et l'aire de la section transversale. Pour une boucle circulaire de rayon b constituée d'un fil conducteur (forme cylindrique) de rayon a (fig 2.10), la longueur du conducteur vaut l = 2ð.b; S la section totale dans laquelle le courant circule effectivement vaut S = 2ða.ä, ce qui caractérise l'effet de peau lié à la circulation du courant RF dans «l'épaisseur de peau» ä du conducteur. ä dépend de la fréquence de travail f et est

donné par:

r ñ

ä = (2.17)

ðfu0

Où ñ est la résistivité du conducteur ( ñ=1.68*10-8m.Ù pour le cuivre) f est la fréquence d'accord de la bobine et u0 est la perméabilité magnétique dans le vide.

Mémoire de Master of science de Physique, par Severin Didjeu. UYI

2.4. SIMULATION D'UNE ANTENNE DE SURFACE : CAS D'UNE ANTENNE

SIMPLE BOUCLE CIRCULAIRE 31

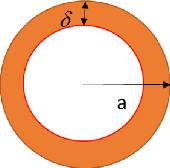
FIGURE 2.10 - conducteur cylindrique de rayon a et de section S caractérisé par l'épaisseur de peau ä [25J

La résistance de la bobine peut être calculée comme suit :

Rbobine(f) = ñ2ðb ðfu0ñ (2.18)

2ðaä ? Rbobine(f) = b \/

a

* Calcul de résistance induit par l'échantillon

Pour estimer les pertes dues à la résistance induite par l'échantillon, nous avons utilisé une méthode utilisant le calcul de potentiel vectoriel (VPC) pour l'estimation des pertes d'échantillons. Il est basé sur l'approche magnétostatique, mis en oeuvre mathématiquement pour le calcul de résistance induite par l'échantillon des bobines simples et des géométries d'échantillon. En fonction de la géométrie et de la forme de la bobine, une estimation de la résistance induite par échantillon peut être donnée par :

fRchantillon = óù^2 vol

A * AdV (2.19)

Où ó est la conductivité de l'échantillon, A est le potentiel de vecteur magnétique produit par le courant I circulant dans la bobine; il s'exprime comme suite :

Z A(r) = u0I dl 4ð w c

(2.20)

En moyennant certaines approximations (conductivité constante sur le volume semi-infini de l'échantillon, courant unitaire uniforme dans la boucle), on peut dans le cas d'une boucle circulaire de rayon b réécrire :

Rchantillon = ₃u²

1 0ù0 ²ób³ (2.21)

Mémoire de Master of science de Physique, par Severin Didjeu. UYI