|

Mémoire de Master
L'Histoire des Mathématiques
et la motivation des élèves
Présenté et soutenu par :
LAZARO
Virginie
Encadrant : M. GAUSSIER Hervé
Responsable du
Mémoire : Mme GANDIT Michèle
M2 MEEF 2nd degré
Mathématiques
2015
En vous souhaitant une bonne lecture.
Organisation
technique
Les rendez-vous avec l'encadrant de mémoire ont eu lieu
aux dates suivantes :
14 Janvier 2015 3 Février 2015 25 Février 2015 11
Mars 2015 1er Avril 2015 22 Avril 2015
Présentation
12-13 Mai 2015
Nous tenons à informer tout lecteur du sens du terme
« motivationnel » que nous avons employé à de multiples
reprises : c'est un adjectif qui signifie dans notre contexte :
« qui concerne la motivation, motivant ».
Sommaire (version numérique)
Introduction 1
I. Étude de recherches 4
I.1. Constatations et motivations 4
I.2. Le « Pourquoi » et le «Comment
» 7
I.3. Les différents types de motivation
11
I.4. Difficultés et contre-arguments
12
I.5. Élaboration de la problématique
15
II. Expérimentations 17
II.1. Séances avec ou sans Histoire
17
II.1.a. Introduction classique des Équations 18
II.1.b. Introduction historique des Équations 19
II.2. Comment introduire l'Histoire des
Mathématiques 21
II.2.a. La pyramide miniature 21
II.2.b. Recherches individuelles 23
II.2.c. Exposé 24
II.3. Bilan et analyse de la motivation 25
II.3.a. Analyse de la pyramide miniature 26
II.3.b. Analyse des Recherches individuelles 28
II.3.c. Analyse de l 'exposé des trois
élèves 31
II.4. Difficultés rencontrées
35
Conclusion 38
Bibliographie 41
Remerciements 42
suite ?
Annexes
Annexe 1. QCM Equations
Annexe 2a. Résultats introduction classique des
équations
Annexe 2b. Résultats introduction historique des
équations
Annexe 3. Sujet activité Euclide
Annexe 4. Sujet activité pyramide miniature
Annexe 5. Sujet recherches individuelles et
exposé
Annexe 6. Diaporama exposé
Annexe 7. Questionnaire motivation
Annexe 8a. Résultats pyramide miniature
Annexe 8b. Résultats recherches
individuelles
Annexe 8c. Résultats exposé
Annexe 9. Copie d'élève
Résumé, Mots-clés / Summary,
Keywords
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
f
f/Ztroductio/Z
« Les Mathématiques ne sont pas une marche
tranquille sur une autoroute dégagée, mais un voyage dans un
désert étrange, où les explorateurs sont souvent perdus
» (W.S Anglin, Mathematics and History). Cette citation nous
rappelle que les Mathématiques ne sont pas une science aisée,
qu'elles résultent d'un processus intellectuel long et sinueux comme la
marche d'un explorateur dans le désert. Certains résultats
mathématiques qui semblent à nos yeux aujourd'hui simples et que
nous enseignons à nos élèves relèvent aussi de
longs développements de la pensée. Malheureusement, ces
évolutions sont très peu révélées aux
étudiants.
Le philosophe Albert Jacquard disait « Sauf pathologie
mentale profonde, tout le monde est bon en Maths. Mais pour des raisons que les
psychologues pourraient sans doute élucider, certains jeunes
décident qu'ils ne sont pas bons. Je crois que la principale
responsabilité réside dans la façon dont les
Mathématiques sont enseignées. » (A. Jacquard, Petite
Philosophie à l'usage des non-philosophes). Cette citation est
également intéressante car elle laisse penser qu'avec une
meilleure approche des Mathématiques dans l'enseignement, il serait
possible que les élèves se sentent plus en confiance dans cette
matière.
Si nous rapprochons ces deux idées, surgit alors une
pensée nouvelle : introduire l'Histoire des Mathématiques dans
l'enseignement pour en faire comprendre les mécanismes et
peut-être ainsi mettre les élèves dans une situation de
réussite et de motivation. C'est exactement l'objet du mémoire
que nous présentons ici.
Ce mémoire est rédigé conjointement par
Madame FRACKOWIAK Cécile et Madame LAZARO Virginie, toutes deux
étudiantes en deuxième année de Master MEEF
(Métiers de l'Enseignement, de l'Éducation et de la Formation)
second degré mention Mathématiques à l'ESPE (École
Supérieure du Professorat et de l'Éducation) de Grenoble et
fonctionnaires stagiaires suite à l'obtention du CAPES (Certificat
d'Aptitude au Professorat de l'Enseignement du Second degré) de
Mathématiques en 2014.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
2
Madame FRACKOWIAK est actuellement en poste au collège
Jules Flandrin de Corenc (38), où elle a en charge deux classes de
4ème et une classe de 5ème. Ce
collège a la spécificité d'accueillir des
élèves UPE2A (Unité Pédagogique pour
Élèves Allophones Arrivants). Le public est essentiellement issu
de familles favorisées, mais il existe tout de même dans les
classes de grosses différences sociales. Le collège
possède peu de moyens matériels, il peine à équiper
les salles en vidéoprojecteurs et en tableaux interactifs.
Madame LAZARO est en poste au collège Le Moucherotte au
Pont-de-Claix (38), où elle a en charge une classe de
6ème, une classe de 4ème, ainsi que
quelques autres élèves de 6ème en PPRE (Projet Personnel
de Réussite Éducative) et des élèves de
5ème en tutorat. Le collège est classé REP
(Réseau d'Éducation Prioritaire). Les financements liés
à cette spécificité ont permis l'équipement de
toutes les salles de classe en vidéoprojecteurs. L'établissement
possède également deux tableaux interactifs et une belle salle
informatique.
Cette collaboration s'est présentée comme
évidente. En effet, nous avons ressenti un grand intérêt
toutes les deux pour l'Unité d'Enseignement « Histoire et
Épistémologie des Mathématiques »
présentée dans le cadre de notre Master. Nous avons
été sensibilisées au message pédagogique qui s'est
dégagé de cet enseignement : connaître l'Histoire des
Mathématiques pour mieux les appréhender.
Nos différentes affectations en termes de milieux
sociaux nous ont semblé être une richesse pour notre projet. Les
expérimentations de certaines activités sur des classes de
même niveau scolaire (4ème) mais issues de milieux
différents peuvent être intéressantes à
étudier. Les différences au niveau des moyens attribués
à chaque établissement pourraient devenir une source de
comparaison.
Enfin, nous nous connaissons depuis plusieurs années et
nous avons l'habitude de collaborer, c'est donc tout naturellement que nous
avons décidé de travailler ensemble.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
3
Notre mémoire comporte une étude
bibliographique. Cette partie s'articule tout d'abord autour du travail de
David Guillemette, doctorant en éducation à l'université
du Québec à Montréal, qui a porté un regard
critique sur la méthodologie des recherches effectuées autour de
l'utilisation pédagogique de l'Histoire des Mathématiques. Nous
avons aussi particulièrement analysé des articles d'Uffe Thomas
Jankvist qui a travaillé sur une catégorisation liée
à l'introduction de l'Histoire des Mathématiques en classe, Siu
qui a fermement critiqué cela, ainsi que le travail de Viau sur les
différents types de motivation chez l'élève.
L'étude d'autres textes nous a enfin menées à poser une
problématique claire, guidant la suite de notre travail :
L'Histoire des Mathématiques peut-elle
être un facteur motivationnel pour les élèves ?
Comment
l'utiliser ?
Nous exhibons ensuite les expérimentations
élaborées en vue des réflexions issues des textes
étudiés, et réalisées pour répondre à
notre questionnement. La première expérimentation a permis une
analyse de l'utilisation de l'Histoire dans nos classes et nous a
confortées dans notre idée qu'elle pouvait être un facteur
motivationnel pour nos élèves. La deuxième partie de nos
expérimentations a pu orienter notre travail sur le « comment
» exploiter au mieux l'introduction de l'Histoire dans notre pratique
professionnelle. Aussi, nous commentons et analysons nos résultats et
nous essayons de répondre à notre problématique. Enfin,
l'analyse de nos observations nous a conduites à détailler les
difficultés auxquelles nous avons été
confrontées.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

I. Etude de recherches
I.1. Constatations et motivations
En France, l'Histoire des Mathématiques n'est pas
considérée comme une matière à part entière
dans le cursus des élèves du secondaire, elle n'apparaît
comme un objet d'étude en soi que dans les cursus universitaires et plus
particulièrement dans celui des enseignants et des chercheurs. Cependant
dans le Bulletin Officiel, on y retrouve quelques références qui
invitent les professeurs à l'intégrer à leurs
enseignements. Ainsi on peut lire que « l'Histoire de l'Humanité
est marquée par sa capacité à élaborer des outils
qui lui permettent de mieux comprendre le monde, d'y agir plus efficacement et
de s'interroger sur ses propres outils de pensée [...]. Au terme de la
scolarité obligatoire, les élèves doivent avoir acquis les
éléments de base d'une pensée mathématique. »
Ces recommandations sont suivies un peu plus tard d'éléments
aidant à la mise en oeuvre de ce projet. Par exemple dans la liste de
types de travaux pouvant être réalisés en autonomie par les
élèves chez eux, il est suggéré de leur proposer
d'effectuer des « lectures ou recherches documentaires, en particulier sur
l'Histoire de la discipline ou plus généralement des sciences
pour enrichir les connaissances ». Enfin « certains problèmes
peuvent prendre appui sur des éléments empruntés à
l'Histoire des Mathématiques ». L'Histoire des Mathématiques
n'est donc pas laissée de côté en France, mais elle ne
possède pas de programme spécifique et est peu
encadrée.
Parmi les recherches effectuées autour de
l'intégration de l'Histoire des Mathématiques dans les classes du
secondaire, l'une d'entre elles se distingue des autres car elle fait le point
sur toutes celles réalisées jusqu'alors. Il s'agit du travail de
David Guillemette, doctorant en éducation à l'Université
du Québec à Montréal. Il présente une analyse des
apports pour les apprentissages des élèves et des
méthodologies de recherches dans le domaine de l'introduction de
l'Histoire des Mathématiques.
Pour mieux comprendre les motivations de David Guillemette et
de ses compatriotes au sujet de l'utilisation de l'Histoire, nous pensons qu'il
est important de rappeler quelle place lui est faite au sein des programmes
québécois. Il est clairement indiqué que
l'intégration de l'Histoire doit être effectuée en classe
pour permettre aux élèves de comprendre le sens et
l'utilité des Mathématiques, de cerner les liens entre cette
matière et les
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

besoins de la société qui ont
évolué au cours des temps, mais aussi de comprendre que les
Mathématiques sont le fruit de longs travaux comme nous l'avons
déjà souligné dans l'introduction. Contrairement au
programme français, les Québécois semblent plus exigeants
sur l'utilisation de l'Histoire. Plus qu'une suggestion, l'insertion de
repères historiques est ici obligatoire et complètement
intégrée au programme. Des domaines précis doivent
être évoqués en classe : l'élève « a
l'occasion de découvrir des mathématiciens qui ont marqué
l'Histoire de la Géométrie et de la Mesure, par exemple Euclide
ou Thalès. Il étudie l'évolution du calcul de la valeur
it, un nombre qui a de tout temps fasciné les gens. Il résout des
problèmes de mesure sur lesquels plusieurs mathématiciens se sont
penchés au cours des siècles, par exemple le calcul de la
circonférence de la Terre (Ératosthène), du rayon de la
Terre, de la distance entre la Terre et la Lune ou de la hauteur d'une
pyramide. Certains instruments de mesure ont traversé les époques
et d'autres ont été perfectionnés ; l'élève
découvre ces instruments ainsi que l'emploi de différentes
unités de mesure. ». Des indications sont également
données aux enseignants sur les moyens de procéder pour
introduire ces notions : « Que ce soit notamment par le moyen de
situations-problèmes, de capsules historiques, de recherches,
d'activités interdisciplinaires ou d'un journal ».
L'introduction de l'Histoire des Mathématiques semble
donc plus aboutie au Québec qu'en France et fait l'objet de recherches
plus poussées, les expérimentations sont aussi plus
nombreuses.
David Guillemette, dans son article intitulé
Enseignement des Mathématiques et Histoire des mathématiques
: Quels apports pour l'apprentissage des élèves ?, distingue
deux types de travaux de recherches. Les premiers sont les travaux de
recherches sous forme de récits de pratiques réalisées en
classe qui sont ensuite analysées. Mais ces travaux possèdent de
gros problèmes méthodologiques que nous détaillerons plus
tard. Les seconds sont les réflexions plus théoriques qui posent
un regard plus aiguisé sur les arguments en faveur de l'utilisation de
l'Histoire des Mathématiques. Guillemette appelle à
accroître le nombre d'expériences pratiques en améliorant
leur qualité. Cela serait la clé pour justifier les trois grandes
hypothèses théoriques faites sur l'apport de l'Histoire des
Mathématiques qu'ont théorisées certains chercheurs :
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
6
Ces trois hypothèses ont été
répertoriées, entre autres, par Évelyne Barbin dans son
document L'Histoire des Mathématiques dans la formation : une
perspective historique (1975-2010).
Elle évoque tout d'abord l'« hypothèse de
dépaysement », également parfois surnommée «
hypothèse de réorientation ». L'Histoire aurait pour but
d'étonner. En effet, les Mathématiques tout au long de leur
construction ne se sont pas présentées comme nous les
présentons aujourd'hui à nos élèves. Elles se sont
construites à des époques et dans des lieux géographiques
différents où les préoccupations et les besoins
étaient différents. Le dépaysement est alors à la
fois mathématique et culturel. Pour les élèves cela est
source de curiosité et pour l'enseignant cela permet de mieux
interpréter les erreurs commises et les questions posées. Pour
obtenir cet apport Barbin suggère l'utilisation de textes originaux sans
aucune modification ni transposition dans un langage moderne.
La deuxième hypothèse est celle de la vertu
épistémologique de l'Histoire. Elle permet de rendre compte de la
transformation d'un concept et de comprendre les liens entre différentes
branches des Mathématiques. La notion de tangente est prise comme
exemple avec son passage d'un problème géométrique pour
les Grecs, à un problème cinématique pour Roberval,
à un problème d'optique pour Descartes. L'Histoire permettrait
également de comprendre les obstacles épistémologiques
qu'ont dû franchir les mathématiciens. Ici c'est l'exemple de la
notion de nombres qui est utilisée pour illustrer le propos. Une
approche épistémologique permet en effet de gommer les erreurs
très fréquentes sur les opérations, sur les nombres
négatifs ou irrationnels.
La troisième et dernière hypothèse est
celle de l'apport culturel de l'Histoire. Elle peut assurément aider
à placer les Mathématiques dans un contexte de pensée
d'une époque et créer des liens profonds avec d'autres
disciplines. Le lien le plus évident qui peut être
créé est celui avec la Philosophie. Par exemple, on a vu
apparaître la volonté de démonstration au moment de
l'établissement de la démocratie grecque. Des rapprochements sont
envisageables avec le domaine littéraire, artistique, économique,
de la Physique ou de l'Histoire.
Dans notre travail expérimental, nous allons nous
concentrer sur la vérification de l'hypothèse de
dépaysement qui est très fortement liée à la
motivation, nous verrons aussi la sensibilité des élèves
à la vertu épistémologique de l'Histoire des
Mathématiques.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
Hypothèses théoriques faites sur l'apport
de l'Histoire des Mathématiques


Dépaysement
|
Vertu épistémologique
|
Apport culturel
|
|
|
Schéma récapitulatif des
hypothèses évoquées par Evelyne Barbin
Guillemette, qui encourage l'expérimentation de ces
trois hypothèses, s'interroge également sur un ordre, ou une
hiérarchisation de celles-ci. Peut-on prouver par
l'expérimentation qu'il y a eu un dépaysement sans observer au
préalable un apport culturel ? Il se questionne également sur les
moyens d'évaluer ces apports. Pour cela il suggère de donner
systématiquement la parole aux élèves à travers des
entrevues, des réflexions écrites, des questionnaires, ou des
productions mathématiques, afin d'obtenir des données solides
à analyser.
I.2. Le « Pourquoi » et le « Comment
» selon Jankvist
De nombreux chercheurs ont tenté de catégoriser
les recherches sur l'introduction de l'Histoire des Mathématiques dans
l'enseignement.
C'est le cas de d'Uffe Thomas Jankvist, un
enseignant-chercheur de l'Université Aarhus au Danemark. En 2009, dans
son article A categorization of the « whys » and « hows
» of using History in Mathematics education*, il
mène un travail important sur une distinction entre deux aspects de
l'utilisation de l'Histoire dans l'enseignement et l'apprentissage des
Mathématiques et leurs corrélations. Nous allons étudier
ses recherches ici.
* Catégorisation des « pourquoi » et «
comment » dans l'utilisation de l'Histoire dans l'enseignement des
Mathématiques
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
8
Tout d'abord, Jankvist parle des méthodes
utilisées pour introduire l'Histoire des Mathématiques en classe
: le « comment ». Il y a selon lui trois façons d'introduire
et de présenter la dimension historique dans l'enseignement des
Mathématiques.
Premièrement, il y a l'approche anecdotique : il s'agit
d'introduire en début ou en fin de cours, ou de séquence, des
faits isolés, des capsules historiques ou anecdotes
particulières. Ce sont des interventions brèves, isolées,
où le professeur fait part de quelques informations historiques : noms
de Mathématiciens, dates, et problèmes qu'ils ont
étudiés par exemple. Cette méthode est très
utilisée au Québec, où notamment Lindstrom (1995) a
créé dans son manuel des petites rubriques historiques à
chaque fin de chapitre concernant les notions abordées.
Ensuite, Jankvist parle de l'approche par module
d'apprentissage. Cette méthode plus répandue consiste en des
capsules d'Histoire plus importantes. Elles peuvent être sous la forme
d'activités autour de l'Histoire, ou de parties de séquences
d'enseignement qui peuvent occuper plusieurs cours entiers. Il peut s'agir de
lectures de textes historiques, d'études de situations-problèmes
ou de projets de recherche menés par les élèves. Les
textes étudiés sont eux-mêmes classés en deux
catégories : les sources primaires et les sources secondaires. Un texte
de catégorie dite « primaire » est un texte original
écrit par un Mathématicien. À sa lecture, un
élève ou un étudiant peut s'en faire sa propre
interprétation et ses propres conclusions. D'un autre côté,
un texte de catégorie « secondaire » est déjà
passé entre les mains d'historiens ou d'experts en Mathématiques.
Ici, les traductions puis améliorations en langage moderne peuvent
biaiser les idées que voulait faire passer l'auteur. En lisant ce type
de document, les élèves perçoivent l'interprétation
de celui qui a manipulé le texte et qui l'a retranscrit. C'est une
approche différente.
Enfin, la troisième méthode citée par
Jankvist est l'approche historique intégrée. Cette approche
diffère des précédentes car elle consiste en un mode
d'élaboration inscrit dans le temps. Lorsqu'un enseignant utilise ce
mode de présentation, il suit en réalité l'ordre
chronologique, donc historique, d'apparition des notions. Par exemple, lors de
l'introduction des types de nombres, le professeur parle d'abord des entiers
naturels, puis des rationnels positifs, ensuite de quelques irrationnels
(toujours positifs) avant de retourner « avant » le zéro et
donc de considérer les nombres négatifs, puis les réels et
enfin les complexes. Cet ordre est exactement celui dans lequel les types de
nombres ont été « trouvés », du moins
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

considérés, car pendant longtemps les hommes ne
voulaient pas concevoir la notion de nombres négatifs. De cette
façon, les élèves ont parfois accès à des
branches des Mathématiques hors-programme mais nécessaires
à l'avancée chronologique vers l'objectif du programme.
Dans un second temps, Jankvist parle des arguments appuyant
l'introduction historique des Mathématiques : le « pourquoi ».
Il y a deux visions différentes de cette utilité.
Pour commencer, l'Histoire des Mathématiques peut
être vue comme un outil motivationnel pour les élèves
lorsqu'elle est introduite en classe. Elle accompagne l'enseignement des
Mathématiques et permet une humanisation de la discipline. Aussi, cet
outil peut aider à montrer que les Mathématiques « ne
tombent pas du ciel ». Les notions du programme prennent une nouvelle
dimension moins abstraite, les élèves découvrent leurs
origines et quelques détails de leurs évolutions au cours du
temps. L'introduction de l'Histoire des Mathématiques peut donc susciter
l'intérêt des élèves pour cette discipline. Jankvist
précise que l'approche historique est considérée comme un
outil si l'intention du professeur reste sur l'objet mathématique
à enseigner.
D'autre part, Jankvist parle de l'Histoire des
Mathématiques comme un objectif en soi. Cette fois l'intention du
professeur est portée sur l'Histoire elle-même, et l'apprentissage
de « l'esprit mathématique ». Dans cette optique, on
considère tout le raisonnement philosophique et socio-culturel qui a
animé les mathématiciens de tous temps dans leurs recherches. On
voit non seulement la finalité du cours qui est l'apprentissage d'une
notion du programme, mais aussi tout le contexte de la pensée et les
barrières rencontrées aux différentes étapes
d'élaboration des notions, comme si les élèves devenaient
des Thalès, Euclide ou Fermat. Ils constatent donc d'eux-mêmes que
les Mathématiques sont en constante évolution dans le temps et
dans l'espace, et que cette évolution est semée d'embûches
et d'impasses.
Dans son article, Jankvist parle de la nécessité
de faire la distinction entre le « pourquoi » et le « comment
», ce qui est peu fait dans la littérature. Il faut éviter
toute confusion entre méthode et argument. Distinguer les deux aspects
ne veut pas dire les isoler, Jankvist aborde d'ailleurs les interrelations
entre ces deux aspects de recherche. Pour mieux
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
comprendre cela, prenons un exemple : imaginons que l'on
veuille faire une approche anecdotique d'une notion, il semble inadapté
de considérer alors l'Histoire comme un objectif en soi. Elle est donc
vue comme un outil. En revanche, l'approche historique intégrée
peut la considérer comme un objectif en soi. Ces interrelations peuvent
être illustrées par le schéma suivant, qui
récapitule aussi toute la catégorisation.
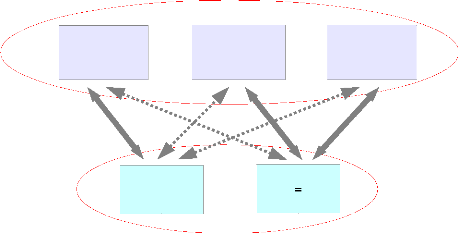
Approche
anecdotique
Histoire
=
outil
Approche
par modules
d'apprentissage
Pourquoi?
Comment?
objectif en soi
Histoire
Approche
historique
intégrée
|
Légende :
|
: interrelations plus adaptées
: interrelations moins adaptées
|
|
Interrelations entre méthodes et arguments
selon Jankvist
Ainsi, cette étude sur la catégorisation des
« pourquoi » et « comment » de l'utilisation de l'Histoire
dans l'enseignement des Mathématiques de Jankvist nous permet
d'éclaircir les méthodes et aspects de l'enseignement de notre
discipline aux élèves. Cela s'avérera très utile
lors de notre expérimentation pour ne pas se perdre dans trop de
manières différentes d'introduire l'Histoire des Maths dans nos
classes, et nous permettra de distinguer clairement nos objectifs.

I.3. Les différents types de motivation
Nous voulons à travers nos expérimentations
évaluer la motivation de nos élèves suite à
l'introduction de l'Histoire des Mathématiques. Il nous a donc
semblé indispensable de comprendre les mécanismes de la
motivation. Selon Viau (2009) la motivation de l'élève est
liée à trois facteurs : la valeur qu'il donne à
l'activité, la perception de sa compétence à la
réussir et la perception qu'il a de lui-même. Plus ces trois
indicateurs sont élevés, plus on peut considérer que
l'élève est motivé. Les deux derniers critères
peuvent être regroupés dans ce que l'on appelle le Sentiment
d'Efficacité Personnelle (SEP) et qui peut être mesuré par
un outil élaboré par Masson en 2011. La motivation peut
être classée en trois catégories distinctes : la motivation
intrinsèque, la motivation extrinsèque et l'amotivation.
La motivation intrinsèque se traduit par le fait que
l'élève réalise l'activité pour son plaisir, sans
attente de récompense. Cette motivation est celle qui donne le plus de
résultats positifs car elle est durable et performante. Pour que
l'élève rentre dans cette dynamique motivationnelle, trois
facteurs rentrent en compte. L'élève doit juger positivement ce
qu'on lui demande de faire (l'activité a de la valeur à ses
yeux), l'élève doit estimer que le degré de contrôle
qu'il exerce sur le déroulement de l'activité est suffisamment
élevé, enfin l'élève doit développer un SEP.
Ces trois sources étant en interaction.
La motivation extrinsèque se traduit par le fait que
l'élève travaille pour faire plaisir à ses parents ou
à son enseignant, pour obtenir une récompense, ou par
nécessité de réaliser la tâche pour atteindre un
objectif plus grand (l'élève fait l'exercice pour avoir son
diplôme ou pour passer dans la classe supérieure). Les causes de
la mise en route d'un tel mécanisme motivationnel sont les suivants : la
vie personnelle de l'élève, la société (valeur,
culture), l'École (règlement, horaire), et la classe (nature de
l'activité, relation élève-professeur, type
d'évaluation, de récompenses ou de sanctions). Ce dernier facteur
étant aux yeux de Viau le plus important.
Ces deux types de motivation sont complétés par
un troisième état : l'amotivation. L'individu a le sentiment
d'être soumis à des facteurs hors de tout contrôle.
L'absence de motivation est liée au sentiment de ne plus être
capable de prévoir les conséquences de ses actions.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
12
À travers nos expérimentations nous
espérons pouvoir mettre en avant pour chaque type d'activité
d'introduction de l'Histoire des Mathématiques la motivation qu'elle
semble engendrer.
I.4. Difficultés et contre-arguments
Malgré l'aspect innovant, original et
intéressant de l'introduction de l'Histoire, des chercheurs prennent du
recul sur ce qui a été fait et certains n'hésitent pas
à critiquer et à donner des contre-arguments à son
utilisation. C'est le cas de Michael N. Fried, un enseignant-chercheur de
l'Université Ben Gourion du Neguev en Israël qui dans son
article Can Mathematics Education and History of Mathematics coexist
?* en 2001 nous fait part de problèmes et difficultés de
mise en place de ce type d'enseignement.
La principale difficulté discutée par les
enseignants et rapportée par Fried est la gestion du temps. En effet,
dans un temps limité, les professeurs doivent enseigner aux
élèves un nombre important de notions, et peinent
déjà à respecter ce programme. L'Histoire ajoutée
étant optionnelle, certains enseignants sont réticents à
son introduction.
Déjà en 1938, Bachelard écrivait que
l'utilisation de l'Histoire pouvait troubler les élèves en les
sortant de leur confort et de leurs habitudes de la discipline.
Par ailleurs, Fried considère qu'il est difficile de
traiter convenablement l'Histoire en classe et voit les anecdotes et capsules
historiques d'un mauvais oeil. Il craint une dénaturation de l'Histoire
qui serait contaminée par une vision moderne des Mathématiques.
L'historicité des concepts tend à se perdre. De plus, les
professeurs se doivent d'enseigner des Mathématiques modernes aux
élèves et de se concentrer sur les savoirs dont ils auront besoin
plus tard dans leurs études scientifiques ou d'ingénieurs.
Comme Le Goff l'a écrit dans un article en 1994,
l'Histoire peut être comme un « écran » devant les
Mathématiques. Fried appuie cet argument en disant qu'avec ce mode
d'enseignement le professeur peut perdre de vue son objectif
mathématique.
Aussi, pour expliquer des notions ou raisonnements
mathématiques, on peut parfois passer par des étapes de
l'Histoire qui par la suite n'ont pas abouti, quel serait alors
l'intérêt de se lancer dans des impasses ?
*Est-ce que l'enseignement des Mathématiques et
l'Histoire des Mathématiques peuvent coexister ?
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

Lors de la dixième conférence de l'ICMI (The
International Commission on Mathematical Instruction) en 1998 à Luminy
sur l'utilisation de l'Histoire des Mathématiques en classe, un
chercheur de l'Université de Hong-Kong, Man-Keung Siu a
présenté à l'assemblée une liste de treize
exclamations et questions, employées à la première
personne sur « pourquoi un professeur devrait hésiter ou se
décider à ne pas utiliser l'Histoire des Mathématiques
dans son enseignement ». Avec le temps et ses collaborateurs, sa liste est
passée à seize points que voici :
1) Je n'ai pas le temps en classe !
2) Ce ne sont pas des Mathématiques !
3) Comment peut-on évaluer cela dans un test
?
4) Les étudiants ne deviennent pas
véritablement meilleurs en Mathématiques !
5) Cela risque de rendre la matière encore plus
complexe à leurs yeux !
6) Les élèves voient ça comme de
l'Histoire et détestent l'Histoire !
7) Les élèves voient ça comme aussi
ennuyeux que le sujet de Mathématiques lui-même !
8) Les étudiants n'ont pas encore assez de culture
générale pour apprécier ce genre d'activité
!
9) Il est ridicule de regarder en arrière quand il
faut constamment progresser avec les élèves !
10) Il n'y a pas assez de ressources sur le sujet !
11) Il n'y a pas assez de professeurs formés pour
cela !
12) Comment être sûr de la précision des
travaux présentés ?
13) Ce qu'il s'est vraiment passé est plutôt
tortueux. Dire ce qui s'est vraiment passé peut être confus,
plutôt que d'éclairer la situation !
14) L'étude de textes originaux est trop difficile
!
15) Cela ne fait-il pas paraître un certain
chauvinisme culturel ou un aspect nationaliste au discours ?
16) Existe-t-il de véritables évidences
empiriques montrant un meilleur apprentissage chez les élèves
lorsque l'Histoire des Mathématiques est introduite dans la classe
?
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

Pour échapper aux difficultés, certains chercheurs
ont tenté d'y apporter des
solutions.
Tout d'abord Avital a écrit en 1995 : « Les
professeurs se demandent 'Où vais-je trouver du temps pour enseigner
l'Histoire ?' La meilleure réponse est : 'Vous n'avez pas besoin de
temps supplémentaire. Donnez juste un problème historique
directement lié au sujet que vous enseignez, dites d'où il vient,
et laissez les élèves travailler eux-mêmes l'Histoire
». La solution d'Avital permet donc au professeur de ne pas « perdre
» de temps mais comme le souligne Fried en 2001, cette réduction
apparente de temps supplémentaire est simplement déplacée
du cours au temps libre des élèves. Est-ce juste de les faire
travailler plus eux ? Fried propose une autre idée qui ne prendrait pas
plus de temps ni au professeur ni aux élèves : il s'agirait de
faire les mêmes cours qu'à l'ordinaire, mais juste avec un
contexte historique. Dans la même optique, le professeur Katz enseigne
les savoirs anciens avec une manière actuelle. Cette dernière
façon d'enseigner est qualifiée par Fried de lecture synchronique
: on décode dans notre système actuel des Mathématiques
anciennes.
Selon Fried, l'utilisation de l'Histoire de la discipline pour
l'enseigner n'est pas à exclure. Il met en garde ses lecteurs en leur
recommandant d'aborder une approche prudente et attentive. Il y a deux
façons de faire : soit on reste en symbiose avec le passé, ce que
Fried appelle « accommodation radicale », soit le cours
mathématique reste séparé du contenu historique, il
appelle cela la « séparation radicale ». Dans le premier cas,
c'est une lecture d'historien que l'on fait des concepts mathématiques :
on cherche à comprendre les notions dans leur contexte historique, il
s'agit d'une lecture diachronique pour Fried. Ce dernier écrit que les
deux types de lecture cités sont à alterner, ce qui est peu fait
par la communauté des enseignants.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

I.5. Elaboration de la problématique
Nous sommes parties d'une étude bibliographique pour
constituer cet état de l'art. Le premier texte étudié a
été celui de David Guillemette, à partir duquel nous avons
pu étayer nos recherches grâce à sa bibliographie. Nous
avons aussi eu accès à la bibliothèque de l'IREM (Institut
de Recherche sur l'Enseignement des Mathématiques) de Grenoble. Nous
avons appris qu'il existait à l'IREM un groupe de recherche sur
l'Histoire des Mathématiques, mais deux obstacles ont fait que nous
n'avons pas pu en rencontrer les membres : tout d'abord leur emploi du temps
chargé ne le permettait pas, et d'autre part nous avons
réalisé que leur sujet d'étude s'éloignait du
nôtre (ils sont plus orientés dans l'utilisation d'outils de
mesure anciens).
Après avoir constaté l'utilisation de l'Histoire
des Mathématiques dans les programmes français et
québécois, nous avons relevé leurs points positifs et
négatifs ainsi que les façons dont les chercheurs la
considèrent et l'utilisent. Nous avons voulu alors formuler une
problématique qui nous permettrait de juger par nous-mêmes, dans
nos classes, si une introduction historique des Mathématiques pouvait
avoir un réel impact sur la motivation de nos élèves, et
si un type d'utilisation serait plus bénéfique. Nous sommes
arrivées à cette formulation :
L'Histoire des Mathématiques peut-elle
être un facteur motivationnel pour les élèves ?
Comment
l'utiliser ?
Les expérimentations et les observations sur le terrain
sont nombreuses mais les analyses qui en sont faites sont, d'après David
Guillemette, peu satisfaisantes en vue du manque de méthodologie de
leurs initiateurs.
Guillemette affirme que dans les recherches actuelles on
constate beaucoup de questionnement quant à l'utilité de
l'Histoire. Guillemette effectue ce travail de rétrospection autour de
la méthodologie employée par les chercheurs. Ses premières
constatations sont édifiantes. Il existe encore trop peu d'études
empiriques dans le domaine de la recherche sur l'utilité de
l'introduction de l'Histoire des Mathématiques dans le secondaire. Peu
de ces études analysent réellement l'évaluation et
l'efficacité de la démarche utilisée. Guillemette se
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
16
propose donc d'étudier différents grands travaux
pour dégager une méthodologie efficace utile dans le futur pour
les chercheurs désirant étudier ce domaine.
Les observations plus approfondies sur ce qui a
déjà été réalisé ont permis de
constater que la majorité des travaux ont été
effectués par des mathématiciens. Seul Jankvist, parmi les
travaux retenus, avait une formation de didacticien. Les recherches sont
systématiquement qualitatives, personne ne propose une exploration
quantitative. Et enfin, le cadre d'analyse des données n'est jamais
précisé.
Suite à ces observations des critiques sont alors
formulées. Le contexte d'étude n'est pas suffisamment
décrit. Les outils de collectes de données sont trop pauvres, pas
assez détaillés et parfois inadéquats. Les données
recueillies ne permettent pas de conclure correctement à cause du cadre
méthodologique mal défini. Les résultats obtenus
s'éloignent alors du projet initial. Enfin, le cadre analytique n'est
souvent lui non plus pas assez bien défini ce qui rend difficile la
compréhension du lien entre les résultats et les conclusions
formulées.
De ces critiques, Guillemette énonce des
recommandations pour les futurs travaux de recherches dans le domaine qui nous
intéresse ici. Il semble donc indispensable de décrire clairement
la méthodologie adoptée. Les outils de récolte des
résultats doivent être décuplés et
diversifiés. Il faut également effectuer plus de comparaisons de
données, de triangularisation. Enfin, il faut détailler le point
de vue adopté lors de l'analyse des données recueillies afin de
mieux conclure sur l'étude effectuée.
Des questions restent également non
élucidées : comment classer et répertorier les
données récoltées ? Comment parfaire la comparaison des
résultats ? Et évidemment, comment créer un cadre
méthodologique adapté ?
Ces constatations riches en observations et en critiques sur
les travaux de recherches effectués sur l'introduction de l'Histoire des
Mathématiques en classe vont nous permettre de construire nos
expérimentations de manière rigoureuse pour répondre
à notre problématique. Il nous faudra auparavant tenter
d'apporter des éléments de réponse aux questions
laissées en suspens par David Guillemette. Suite à sa lecture
nous sortons convaincues qu'une description précise de notre
méthodologie, des outils de collectes et du cadre analytique va nous
permettre de donner de la valeur à nos conclusions.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

II. Expérimentations
Nous voulons à travers notre expérience sur le
terrain observer l'impact de l'Histoire des Mathématiques sur la
motivation des élèves. Nous avons pour cela dans un premier temps
choisi de tester une séquence d'algèbre réalisée
avec l'appui de l'Histoire des Mathématiques et de la comparer avec la
même séquence traitée de façon plus classique. Cette
première expérience menée de façon
méthodique va nous permettre de tirer les premières conclusions
en réponse à notre problématique. Nous avons ensuite
choisi d'approfondir la question, en cherchant à comparer
différents moyens d'utiliser l'Histoire des Mathématiques et
d'observer leur efficacité. Pour cette deuxième partie nous avons
cette fois choisi le thème du théorème de Thalès et
donc de la géométrie.
Nous décrirons pour chacune des expériences
menées la méthodologie adoptée, le déroulement de
la séance et nous analyserons les informations recueillies afin d'en
tirer les conclusions les plus pertinentes possibles. Nous évoquerons
également les difficultés que nous avons rencontrées
durant nos expérimentations.
II.1. Séances avec ou sans Histoire
Dans nos premières expérimentations nous avons
voulu évaluer l'impact de l'utilisation de l'Histoire des
Mathématiques sur la motivation de nos élèves. Nous avons
pour cela choisi la séquence autour de la résolution
d'équation du premier degré. Ce qui pose problème
habituellement dans cette séquence, c'est la difficulté pour les
élèves à comprendre le statut d'une inconnue, remplacer
une valeur par une lettre ne leur semble pas naturel. Aussi, les
élèves mélangent souvent les opérations dans leurs
résolutions d'équations : ils ne font pas la même chose
dans chaque membre de l'égalité, ce qui fausse la suite. Dans la
classe de 4ème de Madame FRACKOWIAK, la séquence s'est
déroulée de façon classique, alors que dans la classe de
Madame LAZARO le chapitre a été introduit avec une
activité basée sur l'Histoire des équations. Étant
donné que tous nos élèves n'ont pas le même
passé mathématique dans le domaine des équations et du
calcul littéral, nous avons décidé, pour comparer leur
progression à la fin de la séquence, d'évaluer leurs
compétences au début du chapitre. Pour cela nous leur avons
distribué un questionnaire à choix multiple (annexe 1)
visant à évaluer les savoir-faire :
Ø
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
18
Compléter des opérations à trous
Ø Tester une égalité
Ø Traduire un énoncé
Ø Utiliser un tableur
Ces compétences sont celles que l'on peut attendre
d'un élève en fin de 5ème dans le domaine des
équations. À la fin de ce chapitre, nous attendons de nos
élèves qu'ils puissent acquérir les compétences
suivantes :
Ø Savoir résoudre une équation du premier
degré à une inconnue
Ø Mettre en équation un problème concret et
comprendre la notion d'égalité.
Pour vérifier l'acquisition de ces compétences
nous avons analysé les devoirs surveillés de nos
élèves effectués en fin de chapitre. Nous avons alors
comparé les résultats des deux classes (annexes 2a et
2b) pour conclure sur l'efficacité d'une introduction
historique.
II.1.a. Introduction classique des Equations
Dans la classe de Madame FRACKOWIAK, les résultats du
QCM montrent que la majorité des élèves (67%)
réussissait à trouver la solution des opérations à
trou proposées avant le début du chapitre. En revanche seulement
38% des élèves ont su tester une égalité, 46 %
arrivaient à traduire un problème simple en une équation.
À l'issue du chapitre, le devoir surveillé a permis de constater
que 69% des élèves ont réussi à tester correctement
une égalité, 62% à traduire un énoncé, et
85% à résoudre les équations proposées pendant ce
test (cette dernière compétence est à comparer avec la
résolution d'opérations à trou en début de
chapitre). Ces résultats indiquent que les élèves ont
réussi, pour ce devoir, à acquérir les compétences
visées. Bien que la grande majorité d'entre eux ait su
résoudre les équations proposées, on constate tout de
même que les élèves ont eu beaucoup plus de
difficultés à traduire un énoncé. Aussi, il a
été difficile de leur apprendre les propriétés sur
les équations, ils ont trouvé cela très calculatoire et
théorique.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

II.1.b. Introduction historique des Équations
Dans la classe choisie pour cette expérience par Madame
LAZARO, le QCM a été fait en amont du nouveau chapitre. Il s'est
avéré que les élèves avaient peu de souvenirs de
5ème, seulement 60% d'entre eux savaient résoudre une
équation (présentée comme une opération à
trou), 30% ont su vérifier une égalité, et enfin 40%
traduire un problème simple en équation. Ces premiers
résultats ont donc été un peu moins bons que dans la
classe de Mme FRACKOWIAK dans l'ensemble.
La première activité introduisant la
séquence « équations » s'est faite autour de l'Histoire
de cette notion. En effet, nous sommes « partis » le temps d'une
séance en 300 avant JC, au temps du mathématicien Euclide, en
Grèce antique. Pour commencer la séance et capter l'attention des
élèves, leur professeur a lu une petite introduction
résumant la biographie d'Euclide et la principale de ses oeuvres :
Éléments. Les élèves ont
écouté avec attention et dans un silence inhabituel. Ensuite, les
sujets d'activité ont été distribués (annexe
3) et la classe a pu découvrir la présence de sept phrases
bien mises en évidence comme si elles avaient été
écrites à la plume. Madame LAZARO a alors formé des
groupes de trois élèves, mélangeant leurs niveaux et leur
implication habituelle dans le cours. Chaque trio devait analyser une des sept
phrases, qui étaient en réalité des postulats
écrits par Euclide dans les Éléments, en faisant
une lecture synchronique au sens de Fried : traduction dans notre
système de notation actuel des Mathématiques anciennes.
Le travail s'est poursuivi dans le calme, chaque membre de
chaque groupe exprimant son idée, comme si leur
hétérogénéité s'était effacée.
Les élèves ont écrit une trace de leurs idées sur
une feuille et ont dû passer au tableau devant leurs camarades groupe
après groupe pour présenter le postulat qu'ils avaient à
étudier. Comme attendu, les résultats présentés par
les élèves n'ont pas été très bons, ils ont
eu du mal à transcrire en langage mathématique actuel les phrases
en langage naturel d'Euclide. Le but de cette activité n'était
pas qu'ils réussissent cette retranscription, mais qu'ils essaient. En
essayant, ils se sont rendus compte du grand écart de notation entre
l'antiquité et nos jours. Leur captivation pour cette
étrangeté, de ne pas réussir complètement à
traduire une phrase en apparence simple, a servi de tremplin à Madame
LAZARO pour présenter la notion d'équation et ses
propriétés contenues dans les postulats. Une mise en commun a
donc été faite, jusqu'à aboutir avec
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
20
l'enseignante aux phrases et propriétés
mathématiques attendues. Une fois que les élèves ont
compris le principe avec les premiers postulats, leur professeur leur a
donné un peu de temps supplémentaire pour réussir seuls
à (re)transcrire les autres, ce qui a été plus facile
cette fois.
Ainsi, les élèves ont écrit par
eux-mêmes, bien qu'ils aient été débloqués
par leur professeur, leurs premières équations en
découvrant les propriétés. Madame LAZARO a profité
de cette activité pour montrer aux élèves à quel
point les notations mathématiques avaient évolué avec le
temps, entre la phrase naturelle d'Euclide et l'ensemble des symboles, chiffres
et lettres d'aujourd'hui. Cela a permis aux élèves de constater
la vertu épistémologique de l'Histoire comme
l'énonçait Barbin. En effet ils ont pu se rendre compte de
l'évolution du concept étudié. L'illustration suivante a
été projetée au tableau :
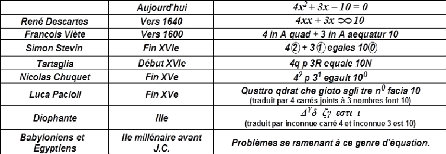
Présentation d'une équation à
travers les époques
La suite de la séquence s'est poursuivie de
manière plus classique, mais chaque résolution d'équation
a remémoré aux élèves leur activité au temps
d'Euclide, ils arrivaient donc à utiliser les propriétés
correctement, sans trouver cela trop abstrait comme dans la classe avec la
présentation classique. Les résultats des évaluations de
fin de chapitre ont d'ailleurs été significatifs : nous pouvons
constater que 80% des élèves de la classe ont réussi
à traduire un énoncé. De même, 80% ont su
résoudre une équation. Les élèves semblent donc
avoir acquis, pour ce devoir, les compétences visées et cela de
manière plus significative que dans la classe de Madame FRACKOWIAK. Pour
la dernière compétence, 70% des élèves ont su
tester une égalité. L'avancée ici est à peu
près similaire à l'autre classe.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
21
On peut donc penser que l'Histoire des Mathématiques a
eu un impact sur les résultats des élèves. Les
élèves ont pu se rattacher à l'activité
d'introduction durant toute la séquence pour progresser dans la
méthode de résolution d'équations. Nous espérons
donc avoir réussi à leur faire comprendre le sens des
équations à travers l'étude de leur Histoire.
II.2. Comment introduire l 'Histoire des
Mathématiques
Nous avons, dans la première partie de nos
expérimentations, mis en valeur les possibles bénéfices de
l'Histoire des Mathématiques sur les apprentissages et notamment du
point de vue de la réflexion sur le sens des objets
étudiés. Les trois situations d'apprentissage auxquelles nous
avons pensé nous ont été inspirées du travail de
Jankvist : l'intégration de l'Histoire avec une approche historique
intégrée, l'approche par module, et enfin l'approche anecdotique.
Ces trois procédures ont été réalisées
à travers trois expériences différentes, introduisant la
séquence de 4ème sur le théorème de
Thalès. En situation d'apprentissage classique de cette notion, les
obstacles didactiques à surmonter sont l'oubli des hypothèses du
théorème et une mauvaise écriture des rapports
égaux. Ces difficultés sont principalement dues à une
mauvaise compréhension du lien entre le sens du théorème
et la proportionnalité. Pour évaluer l'impact de ces
expériences nous avons décidé tout d'abord
d'étudier le comportement des élèves face à ces
activités, ce qui nous permettra une première approche de leur
motivation.
II.2.a. La pyramide miniature
Pour introduire le théorème de Thalès
lors de cette première expérience réalisée dans la
classe de Madame LAZARO, nous avons choisi de leur faire découvrir son
histoire qui a commencé en 600 avant JC avec Thalès. Dans le
cadre d'une approche historique intégrée selon Jankvist, nous
avons utilisé un extrait du livre Le théorème du
Perroquet de Denis Guedj qui raconte l'arrivée de Thalès en
Égypte et sa stupéfaction face à la découverte de
la gigantesque pyramide de Khéops. Nous avons modifié quelques
mots et sauté quelques phrases pour faciliter la compréhension
des élèves. Ce passage a été lu par leur professeur
au début de la séance.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
22
Pour motiver des élèves dans la matière
abstraite des Mathématiques, nous avons voulu faire notre introduction
historique de manière concrète, avec des objets de la vie
réelle à manipuler. Nous avons donc décidé de
construire une mini-pyramide de Khéops, à l'échelle 1/1000
par rapport à la vraie, permettant une immersion temporelle et spatiale
dans l'Histoire. Le but des élèves était alors de trouver
une méthode pour évaluer la hauteur de la pyramide, sans faire
une mesure directe. Ils se sont donc mis dans la situation de Thalès au
pied de la pyramide, qui bien sûr n'avait pas de moyen de la mesurer
directement. Ils avaient à leur disposition le matériel
indiqué sur le sujet (annexe 4 + photo ci-après).

Pyramide de Khéops miniature et
matériel utilisé (+ lampe)
Cette activité s'est déroulée en
plusieurs étapes. Les élèves ont d'abord travaillé
individuellement, afin de tous élaborer une première
méthode. Ensuite, leur enseignante a constitué des groupes de
quatre élèves (cinq groupes) ; groupes réfléchis
à l'avance, constitués d'un élève très
« bon », d'un élève moins bon mais très
participatif, d'un élève moins à l'aise en
Mathématiques et d'un élève « dissipé ».
Les rôles ont été définis :
· Un représentant pour effectuer des mesures sur le
montage
· Un responsable du temps
· Un « maître du silence »
· Un « scribe » (celui qui écrit, en
Égypte !)
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

Les quatre élèves ainsi réunis ont
ensuite dû comparer leurs méthodes, et élire celle qui
selon eux était la meilleure. Une fois une méthode choisie,
chaque groupe est venu effectuer une mesure sur le montage dans une salle
attenante plongée dans l'obscurité. Le représentant
réalisait l'expérience avec l'aide de ses camarades. Les mesures
ont ensuite été collectées. Enfin, une conclusion a
été faite en classe, en étudiant la différence
entre les mesures observées et la réalité, puis
grâce à un tableau de proportionnalité (notion
déjà vue en 5ème l'an passé) la hauteur de la vraie
pyramide de Khéops a été calculée. Pour conclure,
une animation vidéo projetée au tableau a permis de revenir sur
la méthode réellement utilisée par Thalès.
II.2.b. Recherches individuelles
Dans notre seconde expérience, réalisée
dans la classe de Madame FRACKOWIAK, nous avons décidé de mettre
les élèves au coeur de l'action, puisque c'est eux qui ont fait
les recherches dans le domaine historique. Tous les élèves de la
classe ont reçu un court énoncé (annexe 5) leur
indiquant de faire une recherche sur la vie de Thalès, sur ses
différents travaux et sur la façon dont il a mesuré la
hauteur de la grande pyramide de Khéops. Aucune indication
supplémentaire n'a été fournie afin de ne pas les guider
davantage dans leurs recherches, et ne pas créer de biais dans notre
expérience.
Les travaux furent ramassés une semaine plus tard, et
nous avons analysé leur qualité. Nos critères
d'évaluation ont été l'exactitude, la quantité et
la pertinence des informations fournies, ainsi que la présence ou non de
schémas explicatifs. Pour la mesure des dimensions de la pyramide, nous
avons également analysé si les informations étaient plus
du domaine historique, ou du domaine mathématique.
Lors de la séance où les devoirs ont
été ramassés, une mise en commun des informations a
été réalisée sous le contrôle de Mme
FRACKOWIAK. Les éléments essentiels sur la vie de Thalès
ont été rappelés, puis l'explication complète sur
la mesure de la pyramide a été détaillée. Lors de
ces échanges, les élèves n'étaient plus en
possession de leurs copies et ont donc dû faire appel à leur
mémoire et ainsi montrer le sérieux de leurs recherches. Ils
furent très nombreux à participer à cet échange, ce
qui montre une certaine motivation de la part de l'ensemble de la classe. Cette
motivation est d'autant plus satisfaisante que des élèves
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
24
de nature réservée ont également
participé à cette mise en commun. Ce bilan a permis aussi de
rectifier quelques erreurs commises par les élèves, notamment sur
la mesure de l'ombre de la pyramide, avec la conclusion sur sa hauteur. La
réalisation de ces recherches par les élèves peut
être vue comme une approche par module de l'Histoire selon Jankvist, et
la mise en commun en classe peut être vue comme une approche anecdotique,
toujours selon Jankvist. Grâce à cette expérience, nous
allons pouvoir analyser l'efficacité de ces deux approches sur la
motivation des élèves.
II.2.c. Exposé
Pour cette dernière expérience,
réalisée dans la seconde classe de 4ème de
Madame FRACKOWIAK, nous avons demandé à seulement trois
élèves de réaliser un petit exposé sur
Thalès, le sujet leur ayant été posé comme dans
l'expérience précédente (annexe 5). Une seule
consigne supplémentaire a été formulée :
réaliser cet exposé à l'aide d'un diaporama afin de
faciliter la présentation de leurs recherches aux autres
élèves. Trois élèves se sont portés
volontaires pour ce travail. L'un d'eux est un élève ayant de
grosses difficultés en Mathématiques, le second est assez
irrégulier dans son travail et dans ses résultats, et le dernier
se trouve être un élève ayant des facilités en
Mathématiques. Cette différence de profil parmi ces volontaires
sera intéressante à étudier dans notre analyse. Ces
élèves ont eu quinze jours pour préparer leur travail.
Le jour de leur oral, les élèves ont donc
utilisé un diaporama (annexe 6) et avaient également
préparé un script pour les aider dans leur présentation.
Ils ont correctement détaillé les différents points
demandés, avec des informations précises et un visuel attrayant.
Pendant leur présentation, l'ensemble de la classe s'est montré
particulièrement attentif, et Mme FRACKOWIAK n'est pas intervenue. Cette
expérience nous a permis d'analyser l'approche par module selon Jankvist
d'une autre manière que par l'expérience
précédente. Nous avons comparé la motivation des
élèves volontaires, avec leurs trois profils différents,
avec celle du reste de la classe.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
25
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
II.3. Bilan et analyse de la motivation
Dans cette troisième sous-partie nous nous attarderons
à montrer les possibles avantages de l'Histoire des Mathématiques
sur la motivation des élèves dans les différentes
situations d'apprentissages présentées précédemment
sur l'introduction historique du théorème de Thalès.
Nous avons voulu aller plus loin que dans les études
déjà menées et faire une analyse qualitative et
quantitative de la motivation, alors que les études souvent faites
étaient uniquement qualitatives. Notre méthodologie consiste
à prendre en compte les différents types de motivation
étudiés (extrinsèque, intrinsèque, amotivation).
Grâce à notre étude bibliographique nous avons compris
leurs mécanismes et nous avons pu mettre en place un questionnaire
(annexe 7) permettant de juger l'efficacité de chaque type
d'activité sur chaque type de motivation.
La première partie du questionnaire a permis de
constater si l'élève était soumis à une motivation
intrinsèque ou extrinsèque, ou s'il était amotivé.
Les questions posées tournaient autour des Mathématiques, mais
aussi de l'introduction de l'Histoire des Mathématiques. Les
élèves ont dû, pour chacune de leurs réponses,
donner une note de 1 à 6 à une affirmation. Si l'affirmation
correspondait tout à fait à leur état d'esprit, ils
devaient donner la note de 6, si au contraire cela ne leur correspondait pas,
ils devaient donner une note de 1. Ainsi, l'amotivation a été
évaluée par de faibles notes à ce questionnaire. Les
affirmations du type « j'aime les Mathématiques » ou
« j'étudie l'Histoire des Mathématiques même
lorsque je ne suis pas obligé de le faire » ont permis de
détecter la motivation intrinsèque. En revanche « je
fais des mathématiques pour faire plaisir à mes parents ou
à mon enseignant » permettait d'évaluer la motivation
extrinsèque.
La seconde partie a permis de poser des questions plus
précises sur le Sentiment d'Efficacité Personnelle de
l'élève autour du chapitre du théorème de
Thalès que nous avons traité lors de nos expériences. Nous
avons demandé à nos élèves de se juger sur leur
capacité à comprendre ou à finir leurs exercices sur le
théorème de Thalès, ainsi qu'à se concentrer,
à se motiver ou à s'organiser pendant ce chapitre.
26
Une fois les questionnaires recueillis, la méthode
d'analyse a été mûrement réfléchie.
D'après les travaux de Guillemette qui fait la critique des recherches
précédentes sur l'introduction de l'Histoire des
Mathématiques dans les classes, cette méthodologie reste souvent
assez floue. Nous tâchons ici de la détailler au mieux.
Grâce à la première partie de notre
questionnaire nous avons rempli une feuille de calcul d'un tableur avec les
réponses des élèves. Chaque question avait pour but
d'évaluer soit la motivation intrinsèque soit la motivation
extrinsèque. Selon la moyenne des réponses données par
l'élève dans chaque catégorie nous le classons dans l'un
de ces deux groupes. Si l'élève propose des notes faibles dans
toutes les catégories confondues nous le classons comme amotivé,
si au contraire les notes attribuées sont élevées partout
nous le classons dans une quatrième catégorie, celle des
élèves motivés intrinsèquement et
extrinsèquement. Ainsi cette première partie permet de
désigner, pour chaque type d'activité, quelle motivation elle a
le plus mobilisé.
La deuxième partie du questionnaire a permis
d'évaluer le Sentiment d'Efficacité Personnelle de chaque
élève. Nous avons vu précédemment que plus ce
sentiment était élevé, plus cela signifiait que
l'élève était motivé dans sa tâche. Ainsi
nous allons pouvoir essayer de déterminer avec quelle intensité
les élèves ont été motivés pour chaque
activité. Nous espérons que ceci va nous permettre de
désigner, après comparaison, laquelle des trois activités
a été la plus motivante pour nos élèves.
II.3.a. Analyse de la pyramide miniature
Globalement, cette activité semble avoir
intéressé les élèves. Certains se sont plus investi
qu'à l'accoutumé, signe de motivation de leur part. Ils ont pu
apprendre des choses sur Thalès et son expérience menant au
théorème. Bien que cette approche ait été faite de
façon historique intégrée au sens de Jankvist, nous avons
voulu l'utiliser en tant qu'outil (nous avions vu que ce type d'approche
s'accordait mieux à l'Histoire en tant qu'objectif en soi, mais que
Jankvist considérait quand même tous les types de relations
illustrés par le schéma présenté en I.2.). Cet
outil a donc été utilisé dans le but d'introduire le
théorème de Thalès en évitant les problèmes
souvent rencontrés dans ce chapitre.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
Le texte présenté en introduction (voir sur le
sujet de l'activité, annexe 4) ayant été
tiré d'un roman narrant l'histoire de grands mathématiciens et
leurs recherches à travers une fiction, puis reformulé pour les
élèves, cette source est secondaire. Ainsi les
élèves n'ont pas eu de difficulté à en comprendre
le sens.
Cette activité dans son ensemble a eu une influence
positive sur l'ambiance des cours suivants, les élèves voulaient
toujours faire le lien avec l'Histoire : comment Thalès avait pu
formuler son théorème, avec quels moyens (il n'avait pas de
cahier ou de stylo à son époque !), a-t-il fait d'autres choses ?
La manipulation d'objets concrets a permis aux élèves de se
sentir impliqués dans la situation d'apprentissage, de se sentir dans la
même situation que Thalès, et de sortir de leur quotidien
d'élève assis sur une chaise.
Cette introduction historique a permis de leur montrer que
dans le passé les savants n'ont pas toujours eu à leur
portée le même matériel qu'aujourd'hui, et que les
recherches se faisaient avec les moyens de l'époque. C'est une
réelle prise de conscience, un dépaysement selon Evelyne Barbin.
Mathématiquement, lors de l'apprentissage du théorème tel
qu'énoncé au programme de 4ème, les
élèves ont pu faire le lien avec les rapports de longueurs qu'ils
avaient pu observer sur le montage, surmontant cet obstacle classique. Cela a
rendu la notion plus concrète et accessible, applicable à la
« vie réelle » : ils gardaient à l'esprit
l'élaboration fastidieuse du théorème. Enfin le lien entre
le théorème et la proportionnalité s'est fait
naturellement, il était plus compréhensible en termes de Soleil
et d'ombre que donné directement mathématiquement, comme
Thalès le voyait de ses yeux.
Pour mesurer la motivation des élèves sur cette
activité, et voir s'il s'agissait plus de motivation intrinsèque,
extrinsèque ou si certains restaient amotivés, nous leur avons
proposé le questionnaire spécialement conçu pour cela.
Voici les résultats statistiques de cette enquête (détails
des résultats en annexe 8a). La première partie du
questionnaire a révélé que :
· 26,3 % des élèves de Madame LAZARO furent
motivés intrinsèquement
· 47,4 % étaient motivés
extrinsèquement
· 21,1% étaient motivés à la fois
intrinsèquement et extrinsèquement
· 5% étaient amotivés.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'

Motivation et pyramide miniature
Pourcentage motivation intrinsèque:
Pourcentage motivation extrinsèque:
Pourcentage motivation intrinsèque et
extrinsèque:
Pourcentage d'amotivation :
28
L'activité construite autour de l'expérience
avec la pyramide miniature, qui est une approche historique
intégrée, semble avoir majoritairement motivé les
élèves extrinsèquement.
La deuxième partie du questionnaire a permis de
révéler avec quelle intensité les élèves
étaient motivés pour la suite de la séquence sur le
théorème de Thalès à la suite de nos introductions
historiques. On remarque que pour les élèves de Madame LAZARO la
moyenne des notes de SEP est de 3,9 points sur 6. Ce qui nous permet de
conclure que notre activité a plutôt su motiver ces
élèves.
II.3.b. Analyse des recherches individuelles
La réalisation de ces recherches individuelles peut
être vue comme une approche anecdotique au moment de la mise en commun
des recherches mais c'est surtout une approche par module selon Jankvist au
niveau du travail individuel de chaque élève. Peu d'entre eux ont
cité leurs sources, on ne peut donc pas dire si les documents qu'ils ont
étudiés pour leur recherche étaient de catégorie
primaire ou secondaire. Cependant, nous imaginons qu'ils se sont dirigés
vers des sites Internet où les informations ont déjà
été traitées pour faciliter la
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
29
compréhension du lecteur. Quoiqu'il en soit, l'Histoire
des Mathématiques est restée un outil. Ici elle sert
nécessairement à faire passer une notion essentielle du programme
: le théorème de Thalès. Nous pensons avoir en partie
franchi les obstacles rencontrés habituellement durant cette
séquence par l'utilisation de l'Histoire des Mathématiques. En
effet l'étude de l'expérience de Thalès a permis de mettre
en avant la nécessité de l'hypothèse des droites
parallèles. De plus, Thalès a utilisé un bâton dont
il connaissait la mesure, a attendu d'obtenir une ombre égale à
la longueur de ce bâton au sol pour en déduire la taille de
l'ombre de la pyramide et donc sa hauteur. C'est un raisonnement de
proportionnalité que les élèves ont tous compris en
recherchant.
Le fait d'avoir acquis des connaissances historiques sur le
théorème a d'une part permis de surmonter certains obstacles
didactiques, mais elle a également eu des effets sur la motivation. Les
premiers signes visibles ont été ceux observés en classe.
Les élèves se sont beaucoup impliqués lors de la mise en
commun des recherches. Tous ont participé, même les plus
réservés. Chacun cherchait à aller plus loin dans la
précision des réponses apportées par ses camarades. Les
seconds effets visibles ont été ceux observés dans les
copies rendues par les élèves (une copie est proposée en
annexe 9). Ainsi on a pu voir des schémas précis, ou des
dessins illustratifs. Certains textes sur la mesure de la pyramide ont
été romancés. Ainsi on a pu observer que les
élèves ont voulu transmettre le fruit de leurs recherches avec
beaucoup d'application et d'envie.
Enfin le dernier instrument de mesure de la motivation
était celui du questionnaire (annexe 8b). Les premières
questions ont permis de mettre en évidence que :
· 42,1% des élèves de la première
classe de Madame FRACKOWIAK furent motivés intrinsèquement
· 26,3% furent motivés extrinsèquement
· 21,1% furent motivés à la fois
intrinsèquement et extrinsèquement
· 11% furent amotivés
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
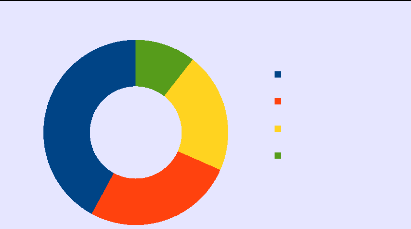
Motivation et recherches individuelles
Pourcentage motivation intrinsèque:
Pourcentage motivation extrinsèque:
Pourcentage motivation intrinsèque et
extrinsèque:
Pourcentage d'amotivation :
30
Ici, on constate que pour cette approche par module de
l'Histoire, les élèves de Madame FRACKOWIAK semblent
majoritairement avoir été motivés intrinsèquement.
Ce qui correspond à un plaisir réel d'accomplir la tâche
demandée.
La deuxième partie du questionnaire a permis de
déterminer l'intensité de cette motivation décelée
chez la plupart des élèves. La moyenne des points de SEP
évaluée dans cette classe est également de 3,9 points sur
6. Ce qui est tout aussi satisfaisant que dans l'expérience
précédente.
Nous pensons que l'élément motivationnel majeur
de cette expérimentation, qui explique les résultats
observés, est la nouveauté liée à l'introduction de
l'Histoire des Mathématiques. Il s'agit d'une motivation
intrinsèque. Nous pouvons tenter d'expliquer ce succès par
plusieurs facteurs :
Ø Nouveauté de la situation d'apprentissage
(motivation extrinsèque)
Ø L'élève se sent responsable dans
l'acquisition des savoirs (motivation intrinsèque)
Ø Réponse aux exigences de l'enseignant
(motivation extrinsèque)
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
31
II.3.c. Analyse de l 'exposé des trois
élèves
La dernière expérimentation que nous avons
menée est une approche par module mais différente de
l'expérience précédente. Ici la transmission des
recherches a été orale, et devait convenir à un public
n'ayant aucune connaissance sur le sujet de l'exposé. Les obstacles
didactiques surmontés grâce à cette expérimentation
ont été les mêmes que précédemment. Cependant
les indicateurs de la motivation des élèves ne sont pas les
mêmes. Il faut, pour les analyser, distinguer deux groupes : les
élèves ayant réalisé l'exposé et le reste de
la classe.
Pour les trois élèves, il faut d'abord noter
qu'ils se sont montrés volontaires pour réaliser cette
présentation. Lors de leur oral, le diaporama présenté
était de bonne qualité, beaucoup de soin a été
apporté à l'esthétique. Le contenu était
également très satisfaisant, puisque l'exposé était
complet et les informations étaient précises et exactes. Les
trois élèves ont fait attention à essayer de rendre
l'exposé le plus clair possible pour se faire comprendre de leurs
camarades. Toute cette implication montre une certaine motivation de la part de
ces élèves pour présenter un travail de qualité.
Une autre preuve du sérieux de leur travail est qu'ils ont réussi
à se faire comprendre sans lire leurs notes pendant leur oral.
Les réponses au questionnaire de ces trois
élèves ont été les suivantes :
· L'élève bon en Mathématiques a
montré une motivation à la fois intrinsèque et
extrinsèque. Son SEP est de 3,8 points sur 6. On peut donc penser en vue
de ces résultats et de son attitude générale pendant
l'expérimentation que l'Histoire des Mathématiques est une
tâche qui l'a au début attiré extrinsèquement puis
qui finalement s'est trouvée être plaisante pour lui.
· L'élève aux résultats moyens en
Mathématiques a manifesté une motivation à la fois
intrinsèque et extrinsèque, bien que l'on puisse analyser que la
motivation intrinsèque est plus importante pour les Mathématiques
que pour son Histoire. Son Sentiment d'Efficacité Personnelle est en
revanche très fort : il est de 5 points sur 6. Cet élève
est pourtant quelqu'un qui d'habitude semble manquer cruellement de confiance
en lui, c'est donc très surprenant d'obtenir des résultats aussi
élevés. Nous pensons que cet exposé lui a permis de
prendre de l'assurance et de se sentir plus à l'aise pour la suite du
chapitre.
·
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
32
Le troisième élève, aux résultats
assez peu satisfaisants en Mathématiques, paraissait avant cette
séquence plutôt amotivé, mais il semble avoir
développé par la suite une motivation intrinsèque. Les
valeurs attribuées aux questions évaluant ce type de motivation
ne sont pas très élevées mais montre une certaine tendance
vers celle-ci pour cet élève. En revanche son SEP est de 1 point
sur 6, ce qui correspond à la note la plus basse que l'on puisse obtenir
à ce questionnaire. On peut donc penser que réaliser cet
exposé est une activité qui lui a plu, mais ne l'a pas
aidé à augmenter sa confiance en lui.
En vue des résultats de ces trois élèves
et de leur attitude avant et durant cette séquence, nous concluons que
la réalisation de cet exposé leur a permis de développer
une motivation intrinsèque, même si son intensité n'est pas
extrêmement élevée.
Pour le reste de la classe ayant suivi l'exposé de
leurs camarades, il faut noter que les élèves étaient
particulièrement attentifs et concentrés pendant la
présentation. Certains d'entre eux ont posé des questions en
complément de ce qui avait été dit, ce qui prouve qu'ils
se sont intéressés au sujet. Cependant, d'autres
élèves semblaient ne pas avoir compris entièrement la
méthode de la mesure de la pyramide car leurs camarades étaient
allés un peu vite dans leurs explications, et on sentait alors pour eux
un peu moins d'implication au moment des questions.
Les questionnaires évaluant la motivation dans le
reste de la deuxième classe de quatrième de Madame FRACKOWIAK
(annexe 8c) ont permis de déceler que :
· 30,4% des élèves étaient
motivés intrinsèquement
· 13 % étaient motivés
extrinsèquement
· 47,8 % étaient motivés
intrinsèquement et extrinsèquement
· 9% étaient amotivés.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
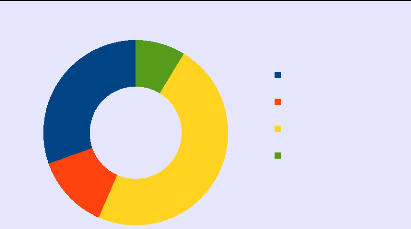
Motivation et exposé
Pourcentage motivation intrinsèque:
Pourcentage motivation extrinsèque:
Pourcentage motivation intrinsèque et
extrinsèque:
Pourcentage d'amotivation :
Il semble donc que majoritairement cette
expérimentation a motivé les élèves à la
fois intrinsèquement et extrinsèquement.
Le SEP est pour cette classe de 4,1 points sur 6, ce qui est
légèrement supérieur à ce qui a pu être
observé lors des précédentes expérimentations. Ceci
peut signifier que la plupart des élèves ont une bonne perception
d'eux-mêmes et de leur capacité à réaliser les
tâches autour de la séquence sur le théorème de
Thalès. Ce qui nous permet de conclure que leur motivation était
assez importante pendant ce chapitre.
Les causes de la motivation chez les trois élèves
volontaires peuvent être multiples :
Ø Comprendre l'Histoire d'un théorème
célèbre (motivation intrinsèque)
Ø La volonté de se valoriser auprès de
leurs camarades et auprès de leur enseignante (motivation
extrinsèque)
Ø Nouveauté de l'activité (motivation
extrinsèque)
Ø Travailler en groupe (motivation
extrinsèque)
Les résultats observés pour le reste de la classe
peuvent avoir les causes suivantes :
Ø Comprendre l'Histoire d'un théorème
(motivation intrinsèque)
Ø Nouveauté de la situation : ce sont des
camarades qui expliquent plutôt que l'enseignante (motivation
extrinsèque)
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
34
Pour conclure sur les trois expérimentations
réalisées, on remarque que pour chaque type d'introduction
semblait correspondre un type de motivation comme le résume le tableau
suivant :
|
Expérimentation
|
Forme d'introduction de
l'histoire
|
Type de motivation observée
|
|
Pyramide miniature
|
Approche historique intégrée
|
Motivation extrinsèque
|
|
Recherches individuelles
|
Module d'apprentissage +
approche anecdotique
|
Motivation intrinsèque
|
|
Exposé des trois élèves
|
Module d'apprentissage
|
Motivation intrinsèque et
extrinsèque
|
Les résultats pour la pyramide miniature peuvent
paraître surprenants car une motivation intrinsèque pouvait
être attendue. Cependant, ils peuvent éventuellement s'expliquer
par le fait que cette activité a été conduite
exclusivement en classe, sous l'impulsion et le dynamisme de Madame LAZARO. Les
élèves ont alors peut-être bien participé à
cette activité pour faire plaisir à leur enseignante. De plus,
l'ensemble de nos expérimentations a été testé sur
un petit échantillon d'élèves, les résultats
observés ne sont donc pas généralisables.
Suite à nos observations, aucune expérimentation
ne s'est démarquée réellement par son efficacité.
Les résultats du questionnaire sur le Sentiment d'Efficacité
Personnelle sont globalement semblables sur les trois expériences.
Cependant, ce sentiment est légèrement plus élevé
dans la classe où l'exposé des trois élèves
volontaires a été réalisé.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
35
II.4. Difficultés rencontrées
Lors de ces expérimentations, et comme Siu notamment en
avait parlé lors de la conférence à Marseille, nous avons
rencontré des difficultés. Celles-ci ont été
d'ordre technique, mais aussi Mathématiques vis-à-vis de nos
élèves.
En effet, comme l'avait rapporté Fried, le premier
obstacle a été le temps. N'ayant pu commencer ce mémoire
qu'en Janvier, nous avons dû revoir l'organisation de nos progressions
scolaires pour arriver aux chapitres désirés au bon moment, en
essayant de faire les expérimentations dans chaque collège de
façon assez simultanée et assez tôt pour pouvoir les
analyser. D'autre part, l'introduction historique des Mathématiques
n'étant pas présente dans les programmes officiels et peu
étudiée en France, il nous a fallu construire des
activités par nous-mêmes. Leur élaboration conjointe a
impliqué des temps de travail entre nous, alors que nos emplois du temps
n'étaient pas toujours compatibles et nos lieux d'habitation
éloignés. La création de la pyramide miniature et de son
sujet nous ont pris le plus de temps à réaliser.
Côté travail en classe, les travaux historiques
ont pris plusieurs séances pour chacun des chapitres introduits de cette
manière. Pour ne pas « perdre de temps » en classe, nous avons
testé la solution d'Avital dans l'expérimentation des «
recherches individuelles ». Mais ce sont alors nos élèves
qui ont dû prendre de leur temps pour étudier d'Histoire des
Mathématiques à travers Thalès. Comme le soulignait Fried,
ce n'était qu'un « déplacement du problème » de
la classe vers chez l'élève. Ainsi notre troisième
solution, celle des exposés, a semblé être au juste milieu
en termes de temps de travail à la maison pour les élèves
(seulement trois), de présentation en classe, et de temps de veille
pédagogique de notre part.
Un autre obstacle avait été évoqué
par Fried, il s'agissait de la peur de dénaturer l'Histoire. Il faut ici
remarquer que les faits historiques que nous avons abordés
étaient clairs et simples, qu'il s'agisse de la lecture des postulats
d'Euclide ou de la méthode de mesure de Thalès, ainsi nos
interprétations ne pouvaient que très peu s'éloigner de la
réalité. Aussi, la crainte de perdre de vue notre objectif
mathématique ne s'est pas faite ressentir, car nos capsules historiques
et les recherches par modules avaient justement pour but d'amener à
comprendre les notions purement mathématiques du programme.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
36
D'autre part, nous avons voulu faire en sorte que ce soit
l'Histoire des Mathématiques qui motive les élèves, ainsi
nous avons dû faire attention à beaucoup de biais. Nous ne
voulions pas rajouter de difficultés supplémentaires par rapport
aux introductions habituelles, c'est pour cela par exemple que le texte au
début de l'activité sur la pyramide miniature a été
simplifié. Aussi, nous ne voulions pas montrer les postulats d'Euclide
aux élèves en Grec ancien par manque de maîtrise de cette
langue, et pour ne pas les effrayer.
L'obstacle le plus difficile à surmonter dans ce
mémoire était la question de l'évaluation de la motivation
des élèves. Comme nous l'avions lu dans un texte de Guillemette,
les observations faites dans ce domaine étaient faibles, nous n'avons
donc pas pu nous inspirer de travaux précédents sur
l'évaluation spécifique de la motivation liée à
l'introduction de l'Histoire des Mathématiques. Il a donc fallu faire
des recherches sur l'étude de la motivation dans d'autres domaines que
les Mathématiques et l'adapter à notre sujet. Là aussi les
ressources n'étaient pas nombreuses mais nous avons tout de même
réussi à construire un questionnaire évaluant
qualitativement et quantitativement la motivation. Cependant, ce questionnaire
n'ayant jamais été utilisé auparavant, on peut
s'interroger sur sa validité. Ce besoin de validité se fait
d'autant plus ressentir que le questionnaire a permis de révéler
des liens inédits entre les types d'introduction de l'Histoire des
Mathématiques et les types de motivation.
L'analyse des résultats n'a pas non plus était
aisée car le classement des élèves par catégorie de
motivation était parfois difficile. Nous avons dû créer une
catégorie « motivation intrinsèque et extrinsèque
» pour pallier notre difficulté à classer certains
élèves.
Nos conclusions sont basées sur un échantillon
de trois classes de 4ème. Pour apporter du poids à
notre travail, il aurait fallu pouvoir tester nos expérimentations sur
plusieurs autres classes, ce qui aurait demandé la mobilisation d'autres
collègues, ou l'observation sur plusieurs années d'enseignement.
Nous aurions aimé également refaire nos expérimentations
sur d'autres chapitres pour appuyer les conclusions effectuées sur nos
classes, mais le temps nous a manqué pour cela. Enfin, nous n'avons
évalué l'impact de l'introduction historique des
Mathématiques que sur un seul niveau. Il pourrait être
intéressant de voir si l'efficacité de cette introduction fluctue
en fonction de l'âge et du niveau des élèves.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
Techniquement pour l'étude de la pyramide miniature, il
fallait une salle assez sombre, et la salle informatique du collège
Moucherotte a bien convenu. Pour les recherches individuelles, il fallait
surtout que les élèves aient accès à un poste
informatique, voir des encyclopédies à la maison (ce moyen est
bien moins utilisé de nos jours). Il nous a donc semblé plus
pratique de faire cette expérimentation dans le milieu plus aisé
de Corenc où beaucoup de familles sont équipées, de
même pour l'exposé.
Mathématiquement, les élèves ont
rencontré des obstacles que nous n'avions pas prévus. Lors de
l'activité historique sur les Equations, un élève a
demandé à Madame LAZARO si « c'était des Maths
». Il est vrai que sur l'énoncé aucun symbole
mathématique n'apparaissait, ce qui a troublé
l'élève, mais le but de l'activité était justement
de voir que c'était bien des Mathématiques mais écrites
d'une façon différente de la nôtre. Cette activité a
dépaysé les élèves, un argument positif cité
par Evelyne Barbin. Malgré la volonté de simplifier les
écritures, les élèves ont eu du mal à comprendre le
sens des mots « choses inégales » dans les postulats
d'Euclide, en effet pour eux cela signifiait « différent de »,
alors que mathématiquement c'était des inégalités
(« > » ou « < » ) qui étaient
désignées.
Aussi, une lacune mathématique s'est faite ressentir
lorsque les élèves ont tenté de faire des mesures sur la
pyramide miniature, confondant hauteur d'une pyramide et hauteur d'une de ses
faces latérales, qui sont différentes. Nous avons compris cette
erreur : nous n'avions pas pensé à faire passer le chapitre sur
la géométrie dans l'espace et particulièrement les
pyramides avant celui sur le théorème de Thalès. Nous
avons alors fait une petite parenthèse durant la séance pour
régler ce problème. Cette difficulté s'est aussi ressentie
dans les recherches individuelles des élèves qui eux non plus
n'avaient pas vu les pyramides.
Enfin, certains élèves (classes « pyramide
miniature » et « recherches individuelles ») n'ont pas
réussi à conclure correctement sur la hauteur de la pyramide, car
ils ont choisi un raisonnement intuitif : pour eux la mesure de l'ombre pouvait
donner la hauteur recherchée, mais ils ont oublié de compter la
moitié du côté de la base de la pyramide pour conclure
correctement. Cette erreur a été évoquée largement
pendant le temps de mise en commun des recherches dans la classe de Madame
FRACKOWIAK.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
38
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
Conclusion
« La démarche vers le savoir n'est pas d'accumuler
de la science, [...] c'est de reconnaître sa propre réalité
dans le monde, et de la juger » a écrit en 1974 Herbert le Porrier.
En tant que professeurs, nous aspirons à apprendre tout au long de notre
carrière, aussi bien Mathématiquement que didactiquement, mais
aussi humainement.
Dans la première partie de ce Mémoire, nous
avons pu faire le bilan des arguments en faveur ou contre l'utilisation de
l'Histoire des Mathématiques en classe déjà établis
par de grands professeurs ou chercheurs. Nous avons alors voulu faire des
observations par nous-mêmes pour constater dans la réalité
de notre quotidien les effets (bénéfiques ou non) sur la
motivation des élèves d'une introduction historique des notions
mathématiques au programme en classe de 4ème au
collège, ainsi que les difficultés que cela pouvait engendrer.
Une analyse préalable des types de motivation a été
réalisée, pour juger ensuite par nous-mêmes de l'impact de
nos expérimentations variées sur nos élèves.
Notre première expérimentation sur
l'introduction historique des Équations nous a tout d'abord permis de
constater que les obstacles didactiques habituellement rencontrés dans
ce chapitre pouvaient être écartés par rapport à une
introduction classique. En réalisant que la notion d'Équation
avait évolué au fil du temps, ne serait-ce que par sa
présentation, les élèves se sont sentis plus
impliqués dans leurs travaux, comme si eux aussi avaient un rôle
à jouer. Par ailleurs, en voulant traduire en langage
mathématique symbolique actuel les postulats d'Euclide écrits en
langage naturel, ils ont pu apprendre inconsciemment les premières
propriétés sur les équations, ce qui a semblé trop
calculatoire et abstrait dans l'introduction de manière classique dans
la classe de comparaison. Tout ceci nous a alors permis de conclure que oui,
l'Histoire des Mathématiques semblait être un facteur
motivationnel pour les élèves.
39
C'est alors que nous nous sommes demandé comment
utiliser l'Histoire de notre discipline, en vue des différents types
d'introductions possibles évoqués dans notre état de
l'art. Nos trois expérimentations sur le théorème de
Thalès nous ont permis de faire quelques comparaisons en termes d'impact
motivationnel.
Il s'est avéré qu'une approche historique
intégrée (selon Jankvist), avec une activité sur « la
pyramide miniature », se traduisait par une motivation extrinsèque
chez les élèves : peut-être que ceux-ci étaient plus
intéressés par faire plaisir à leur professeur que par
leur propre plaisir à se prendre pour « de petits Thalès
» en classe. Toujours est-il que cette activité les a
motivés, les résultats ont montré un Sentiment
d'Efficacité Personnelle plutôt haut. Bémol de cette
activité, le temps de sa mise en place, de la préparation des
salles et du matériel et de son exécution en classe.
L'approche par module (selon Jankvist) consistant en des
recherches personnelles de la part de tous les élèves d'une
classe a semblé plus concluante en ce que nous pensons être la
motivation la plus bénéfique : la motivation intrinsèque.
Ce type d'introduction a aussi été bénéfique sur le
temps passé en classe par rapport à la première
expérience, ce qui est plus avantageux pour le professeur, pas pour les
élèves. Le SEP a aussi été très correct.
Notre troisième façon d'introduire le
théorème de Thalès historiquement grâce à un
exposé a illustré une motivation intrinsèque et
extrinsèque des élèves spectateurs, c'est donc un bilan
positif pour nous. Comme avec les recherches individuelles, ce travail n'a pas
pris trop de temps en classe, et cette fois seuls trois élèves
ont cherché chez eux, ainsi le temps libre de la classe n'a pas
été trop empiété. Le SEP a été
très bon, et les trois orateurs ont globalement profité
positivement de leur travail.
Ainsi, si nous devions choisir la façon la plus
optimale d'introduire historiquement le théorème de
Thalès, nous prendrions la troisième expérimentation, bien
que les deux autres aient également laissé paraître un
impact motivationnel positif. Cependant nous nous demandons si cette mise en
place d'exposés serait possible dans toutes les séquences, et si
les résultats sur la motivation seraient les mêmes.
Aussi, les programmes sont en constante évolution, et
nous pouvons nous demander si un jour en France une place plus importante sera
accordée à l'introduction historique des Mathématiques,
comme c'est déjà le cas au Québec.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
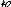
Dans une optique d'élargissement, et en rapport avec la
troisième hypothèse d'Evelyne Barbin sur l'apport culturel (au
sens de « lien avec les autres disciplines ») de l'Histoire des
Mathématiques qui a été peu étudié dans nos
expérimentations, nous pourrions envisager une collaboration entre
professeurs de Mathématiques et professeurs
d'Histoire-Géographie. En effet, quand nous parlons d'Histoire nous
regardons souvent les avancées politiques ou économiques d'un
pays, mais pourquoi ne pas apprendre en même temps les avancées
scientifiques qui sont ensuite étudiées en cours de Science ?
L'Histoire de l'Art par exemple est déjà très
présente et constitue une épreuve du brevet des collèges.
Elle n'est pas enseignée qu'en Arts-Plastiques mais dans de nombreuses
disciplines (Français, Histoire-Géographie, Éducation
musicale par exemple). Il serait intéressant pour les
élèves de faire plus de liens entre les matières du
collège, ils pourraient en apprendre l'Histoire, particulièrement
en cours d'Histoire. Cela pourrait leur montrer l'importance et le sens de
chaque discipline enseignée au collège, et répondre
à leurs questions récurrentes sur la provenance,
l'intérêt et l'utilité des notions étudiées
dans chaque matière.
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
41
Bibliographie
· Barbin Evelyne, L'Histoire des Mathématiques
dans la formation : une perspective historique, 1975-2010
· Bulletin officiel spécial n° 6 du 28
août 2008, Programmes du collège, Programmes de l'enseignement de
mathématiques. Introduction commune.
· Denis Guedj, Le théorème du Perroquet,
Le seuil, 1998
· Fried Michael N., Can Mathematics Education and
History of Mathematics coexist ?,
2001
· Guillemette David, Enseignement des
Mathématiques et Histoire des mathématiques : Quels apports pour
l'apprentissage des élèves ?
· Guillemette David, L'Histoire dans l'Enseignement des
Mathématiques : sur la méthodologie de recherche
· Jankvist Uffe Thomas, « A categorization of the
« whys » and « hows » of using history in Mathematics
education », Educational studies in Mathematic, 2009
· Masson J. Construction et validation d'une échelle
de Sentiment d'Efficacité Personnelle. 2011
· Programme de formation de l'école
Québécoise. Chapitre 6 : Domaine de la mathématique de la
science et de la technologie.
· Siu Man-Keung, No, I don't use history of mathematics
in my class, Why ?
· Viau R., La motivation en contexte scolaire,
Bruxelles : De Boeck, 2009
LAZARO Virginie Mémoire 'Histoire des
Mathématiques et motivation des élèves'
42
Remerciements
Tout d'abord, je tiens personnellement à remercier ma
collègue et amie FRACKOWIAK Cécile pour
l'écriture conjointe de ce Mémoire. Je la remercie pour son
investissement, sa patience et sa bonne humeur.
Nous remercions vivement notre encadrant de Mémoire
Monsieur GAUSSIER Hervé pour ses lectures, son aide
précieuse, ses conseils, sa patience et sa compréhension.
Nous remercions également Madame GANDIT
Michèle pour l'organisation de cette unité
d'enseignement et les informations communiquées.
Aussi, nous remercions grandement Monsieur YCART Bernard
qui nous a transmis sa passion pour l'Histoire des
Mathématiques à travers l'unité d'enseignement du
même nom en ce début d'année de notre Master 2.
Merci aux élèves de la
4ème1 du collège Moucherotte au
Pont-de-Claix, aux 4èmeA et
4èmeC du collège Jules Frandrin
à Corenc pour leur participation aux expérimentations, sans qui
ce mémoire n'aurait pu être écrit.
Nous tenons à remercier CASTAGNA Sophie
et JACQUOT Romain pour leur relecture finale.
Enfin, merci à tout lecteur de ce Mémoire que nous
avons rédigé avec plaisir.
4ènle NOM : QCM
Équations
Pour chaque question, une seule réponse est
exacte. Laquelle ? 1)Compléter une addition à trou
Le nombre manquant pour que l'égalité 2,5 +
? = 7 soit vraie est ...
a) 2,5-7 b)7-2,5 c) 7 : 2,5
2)Compléter une soustraction à trou
Le nombre manquant pour que l'égalité 14 -
? = 5,6 soit vraie est ...
a) 5,6-14 b) 14-5,6 c) 14 : 5,6
3)Compléter une multiplication à trou
Le nombre manquant pour que l'égalité 7,5 x
? = 3 soit vraie est ...
a)7,5-3 b) 7,5 : 3 c) 3 : 7,5
4)Tester une égalité
L'égalité 2x-5=5x-2
est vraie lorsque x est égal
à ...
a) -1 b) 0 c) 1
5)Traduire un énoncé
Alice possède 27 BD . Elle sait qu'elle en a 5 de
plus que le double du nombre de BD de Léa. En notant x
le nombre de BD de Léa, on peut traduire cette situation
par ...
a) x+5=2x27 b)
2x+5=27 c) 2x=27+5
6)Utiliser un tableur
Dans la cellule B2 de la feuille de calcul ci-dessous,
pour calculer 7x-1, on doit écrire, avant de l
'étendre vers le bas la formule ...
a) 7*A2-1 b) =A2-1 c) =7*A2-1
|
A
|
B
|
|
1
|
x
|
7x-1
|
|
2
|
1
|
|
|
3
|
2
|
|
|
4
|
2
|
|
|
5
|
3
|
|
4ènle NOM : QCM
Équations
Pour chaque question, une seule réponse est
exacte. Laquelle ? 1)Compléter une addition à trou
Le nombre manquant pour que l'égalité 2,5 +
? = 7 soit vraie est ...
a) 2,5-7 b)7-2,5 c) 7 : 2,5
2)Compléter une soustraction à trou
Le nombre manquant pour que l'égalité 14 -
? = 5,6 soit vraie est ...
a) 5,6-14 b) 14-5,6 c) 14 : 5,6
3)Compléter une multiplication à trou
Le nombre manquant pour que l'égalité 7,5 x
? = 3 soit vraie est ...
a)7,5-3 b) 7,5 : 3 c) 3 : 7,5
4)Tester une égalité
L'égalité 2x-5=5x-2
est vraie lorsque x est égal
à ...
a) -1 b) 0 c) 1
5)Traduire un énoncé
Alice possède 27 BD . Elle sait qu'elle en a 5 de
plus que le double du nombre de BD de Léa. En notant x
le nombre de BD de Léa, on peut traduire cette situation
par ...
a) x+5=2x27 b)
2x+5=27 c) 2x=27+5
6)Utiliser un tableur
Dans la cellule B2 de la feuille de calcul ci-dessous,
pour calculer 7x-1, on doit écrire, avant de l
'étendre vers le bas la formule ...
a) 7*A2-1 b) =A2-1 c) =7*A2-1
|
A
|
B
|
|
1
|
x
|
7x-1
|
|
2
|
1
|
|
|
3
|
2
|
|
|
4
|
2
|
|
|
5
|
3
|
|
Annexe 1. QCM Equations
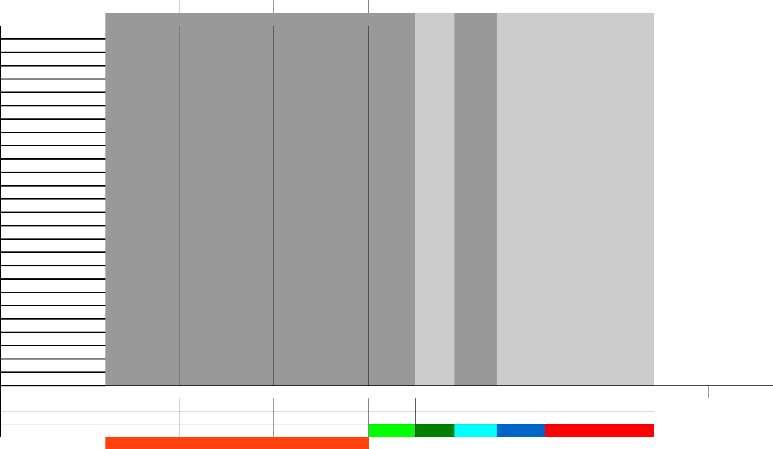
67
Moyenne opérations
après
avant
après après
Addition à trou
Soustraction à trou
Multiplication à trou
Tester une égalité Traduire un énoncé
Résoudre une équation
Nombre bonnes réponses
avant avant avant avant
|
Élève 1
|
oui oui oui oui oui oui oui oui non non oui oui non oui oui non
non oui non oui oui oui oui non non non oui
|
oui oui oui oui oui oui oui oui oui oui oui non non oui oui non
oui oui non non oui oui non non oui oui oui
|
oui non oui oui oui oui non non non non oui oui non oui oui non
oui oui non non non oui oui non non oui non
|
oui oui
non non
oui oui
oui oui
non oui
non oui
non non
oui non
non oui
non non
oui oui
non oui
oui oui
oui non
non oui
non oui
non non
non non
non non
non oui
non oui
non non
non oui
oui oui
oui oui
oui oui
non oui
|
non oui
oui non
oui non
oui oui
non oui
oui oui
non non
non non
non non
non non
non oui
oui oui
oui oui
oui oui
non oui
non non
oui oui
non oui
oui non
non oui
non non
non non
oui oui
oui oui
oui non
non oui
non oui
|
oui oui oui oui oui oui oui non oui oui oui oui oui oui oui non
non oui oui oui oui non oui oui non oui oui
|
|
Élève 2
|
|
Élève 3
|
|
Élève 4
|
|
Élève 5
|
|
Élève 6
|
|
Élève 7
|
|
Élève 8
|
|
Élève 9
|
|
Élève 10
|
|
Élève 11
|
|
Élève 12
|
|
Élève 13
|
|
Élève 14
|
|
Élève 15
|
|
Élève 16
|
|
Élève 17
|
|
Élève 18
|
|
Élève 19
|
|
Élève 20
|
|
Élève 21
|
|
Élève 22
|
|
Élève 23
|
|
Élève 24
|
|
Élève 25
|
|
Élève 26
|
|
Élève 27
|
|
Pourcentage réussite
|
|
nombre de oui
|
18
|
20
|
14
|
10
|
18
|
12
|
16
|
22
|
|
nombre de non
|
9
|
7
|
13
|
17
|
9
|
15
|
11
|
5
|
|
% réussite
|
69
|
77
|
54
|
38
|
69
|
46
|
62
|
85
|
|
Avant
|
Après
|
|
4
|
3
|
|
3
|
1
|
|
5
|
2
|
|
5
|
3
|
|
3
|
3
|
|
4
|
3
|
|
2
|
1
|
|
3
|
0
|
|
1
|
2
|
|
1
|
1
|
|
4
|
3
|
|
3
|
3
|
|
2
|
3
|
|
5
|
2
|
|
3
|
3
|
|
0
|
1
|
|
3
|
1
|
|
3
|
2
|
|
1
|
1
|
|
1
|
3
|
|
2
|
2
|
|
3
|
0
|
|
3
|
3
|
|
2
|
3
|
|
3
|
1
|
|
3
|
3
|
|
2
|
3
|
|
55
|
69
|
avant
après
après après
Moyenne opérations
60
Addition à trou
Soustraction à trou
Multiplication à trou
Tester une égalité
Traduire un énoncé Résoudre une
équation
Nombre bonnes réponses
avant avant avant avant
|
Élève 1
|
oui oui oui oui oui non oui oui oui oui non non oui oui oui oui
oui non oui non
|
non non oui oui oui non oui non oui oui non oui oui non oui oui
oui non non non
|
non non oui non oui non oui non oui oui non non oui oui oui non
oui oui non non
|
non non
non non
non oui
oui oui
non oui
non non
oui oui
non oui
oui oui
oui oui
non oui
non oui
non oui
non oui
oui oui
non oui
oui non
non non
non oui
non non
|
non non
non oui
non oui
oui oui
oui oui
non non
oui oui
non oui
oui oui
oui oui
oui oui
non non
oui oui
non oui
non oui
oui oui
non oui
non oui
non non
non oui
|
non oui oui oui oui non oui oui oui oui non oui oui oui oui oui
oui oui non oui
|
|
Élève 2
|
|
Élève 3
|
|
Élève 4
|
|
Élève 5
|
|
Élève 6
|
|
Élève 7
|
|
Élève 8
|
|
Élève 9
|
|
Élève 10
|
|
Élève 11
|
|
Élève 12
|
|
Élève 13
|
|
Élève 14
|
|
Élève 15
|
|
Élève 16
|
|
Élève 17
|
|
Élève 18
|
|
Élève 19
|
|
Élève 20
|
|
Pourcentage réussite
|
|
nombre de oui
|
15
|
11
|
10
|
6
|
14
|
8
|
16
|
16
|
|
nombre de non
|
5
|
9
|
10
|
14
|
6
|
12
|
4
|
4
|
|
% réussite
|
75
|
55
|
50
|
30
|
70
|
40
|
80
|
80
|
|
Avant
|
Après
|
|
1
|
0
|
|
1
|
2
|
|
3
|
3
|
|
4
|
3
|
|
4
|
3
|
|
0
|
0
|
|
5
|
3
|
|
1
|
3
|
|
5
|
3
|
|
5
|
3
|
|
1
|
2
|
|
1
|
2
|
|
4
|
3
|
|
2
|
3
|
|
4
|
3
|
|
3
|
3
|
|
4
|
2
|
|
1
|
2
|
|
1
|
1
|
|
0
|
2
|
|
50
|
77
|
4ème A la découverte des
équations en Grèce antique
Euclide est un Mathématicien de la Grèce
antique ayant vécu environ en 300 avant J-C. Vous en avez
déjà entendu parler notamment en étudiant la «
division euclidienne ».
Son ouvrage le plus célèbre s'appelle Les
« Éléments », dans lequel il parle de
géométrie et d'arithmétique théorique. On trouve
dans ce livre des théorèmes et leurs démonstrations, mais
aussi des postulats et des axiomes : ce sont des propriétés, des
vérités qui sont admises et que l'on ne démontre pas. Nous
allons en étudier quelques uns, en essayant de les traduire en
Mathématiques modernes.
Par groupes de trois élèves désignés
par le professeur :
a. Expliquer avec vos mots sur une feuille
(avec vos noms) ce que vous comprenez du postulat d'Euclide qui correspond au
numéro de votre groupe.
b. Essayer de traduire ce postulat avec des
symboles mathématiques (+, -, =, x, a,...)
Voici la liste des postulats d'Euclide:
1. Les choses égales à une même
chose sont égales entre elles.
2. Si à des choses égales, on ajoute
des choses égales, les touts seront
.égaux.
3. Si à des choses égales, on retranche
des choses égales, les restes seront
égaux.
4. Si à des choses inégales, on ajoute
des choses égales, les touts seront
inégaux.
5. Si à des choses inégales, on
retranche des choses égales, les restes seront
inégaux.
6. Les choses, qui sont doubles d'une même
chose, sont égales entre elles.
7. Les choses, qui sont les moitiés d'une
même chose, Sont égales entre elles.
c. Groupe par groupe, passer au tableau pour
expliquer à vos camarades ce que vous avez trouvé.
4ème Activité : A la découverte du
Théorème de Thalès en Égypte
« Appuyé sur la rambarde d'un bateau,
Thalès regardait s'éloigner la terre de Milet où il avait
vécu jusqu'à ce jour. Il partait pour l'Égypte.
Après quelques jours de voyage, non loin de la rive du fleuve, il
l'aperçut. La pyramide de Khéops. Thalès
n'avait jamais rien vu d'aussi grand. Un matelot dit à Thalès :
"Cette pyramide a été dressée par le pharaon Khéops
dans le seul but d'obliger les humains à se persuader de leur petitesse.
Le but est atteint. Pharaon et ses architectes ont voulu nous contraindre
à admettre qu'entre cette pyramide et nous il n'y a aucune
commune mesure". C'était une évidence pour tout le monde
: la hauteur de la pyramide était impossible à mesurer. Elle
était la construction la plus visible du mondé habité et
elle était la seule à ne pouvoir être mesurée !
Thalès voulut relever ce défi.
Un matin, lorsque le soleil éclaira l'horizon, debout,
Thalès regarda se déployer son ombre sur le sable. Plus le soleil
montait dans le ciel, plus son ombre devenait petite, jusqu'à faire la
même taille que lui à 10 heures... »

Étape 1. L'Égypte miniature au lever du
Soleil
Nous plongeons la classe dans l'obscurité. Nous avons face
à nous, en miniature :
- Un bâton représentant Thalès (Hauteur : 2
cm)
- Une pyramide en papier (Hauteur : Inconnue)
- Une lampe pour la lumière du Soleil.
Quelques uns d'entre vous vont pouvoir tenir la lampe et ainsi
produire un lever de Soleil sur notre
petit montage. Observez bien tous la situation.
a. De retour à votre place, imaginez comment, grâce
à ce matériel, mesurer la hauteur réelle de la pyramide en
papier. (Rappelez-vous qu'elle représente une immense pyramide
impossible à mesurer directement). Écrivez le protocole (la
méthode) à suivre sur la feuille blanche distribuée.
b. Par groupes de 4 élèves désignés
par le professeur, discutez de vos méthodes pour mesurer la hauteur de
la pyramide en papier. Comparez et sélectionnez la méthode qui
vous semble la meilleure. Écrire cette méthode (si elle est
différente de la votre) sur votre feuille.
c. Un représentant de chaque groupe est choisi. Il vient
sur le montage et explique devant tous ses camarades la méthode
adoptée par son groupe (il peut être aidé d'un ou plusieurs
camarades si besoin). Il l'exécute et dit à tout le monde la
hauteur qu'il a trouvé pour la pyramide en papier. Notez ici les
résultats des différents groupes :
Groupe A : cm Groupe C : cm Groupe E : cm
Groupe B : cm Groupe D : cm
d. La vraie hauteur de la pyramide en papier est (attendre que
le professeur vous
donne cette mesure). Discussions autour des
résultats obtenus. Puis, le professeur explique comment Thalès a
réellement pu mesurer la hauteur de la pyramide de Khéops
(animation).
4C Effectuer une Recherche : Pour le
22/01/2015
-Expliquez qui était Thalès.
-Expliquez avec vos propres mots comment Thalès a
mesuré la pyramide de Khéops. Vous pouvez effectuer un dessin
pour compléter votre texte.

Diapo 2 Diapo 6
Diapo 3 Diapo 7
Diapo 4 Diapo 8
Diaporama réalisé par les 3 élèves
de Madame Frackowiak
Diapo 1 Diapo 5
Questionnaire : Motivation
Consigne : Lis chaque affirmation
attentivement. Réponds le plus honnêtement possible en entourant
à chaque fois le numéro qui correspond le mieux à ce que
tu penses.
1
Tout à fait faux
2
Plutôt faux
3
Un peu faux
4
Un peu vrai
5
Plutôt vrai
6
Tout à fait vrai
J'aime les Mathématiques.
1
|
2
|
3
|
4
|
5
|
6
|
2- L'Histoire des Mathématiques me permet d'apprendre
beaucoup de choses utiles.
|
1
|
2
|
3
|
4
|
5
|
6
|
3- Je fais des Mathématiques pour obtenir une belle
récompense.
|
1
|
2
|
3
|
4
|
5
|
6
|
4- L'Histoire des Mathématiques m'intéresse
beaucoup.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|
5-J'ai choisi de faire de l'Histoire des Mathématiques
pour apprendre plein de choses.
|
1
|
2
|
3
|
4
|
5
|
6
|
|
6-Je fais de l'Histoire des Mathématiques pour faire
plaisir à mon enseignante.
|
1
|
2
|
3
|
4
|
5
|
6
|
7- Je fais des Mathématiques pour faire plaisirs à
mes parents et à mon enseignante.
|
1
|
2
|
3
|
4
|
5
|
6
|
8- J'étudie l'Histoire des Mathématiques
même lorsque je ne suis pas obligé de le faire.
|
1
|
2
|
3
|
4
|
5
|
6
|
9- Dans la vie il est important d'apprendre à faire des
Mathématiques.
|
1
|
2
|
3
|
4
|
5
|
6
|
10- Je fais des Mathématiques pour montrer aux autres
que je suis bon.
|
1
|
2
|
3
|
4
|
5
|
6
|
|
11- J'arrive toujours à finir les exercices sur le
|
1
|
2
|
3
|
4
|
5
|
6
|
|
théorème de Thalès.
|
|
|
|
|
|
|
|
12-J'arrive à me concentrer sur mes exercices sur le
|
1
|
2
|
3
|
4
|
5
|
6
|
|
théorème de Thalès en classe.
|
|
|
|
|
|
|
|
13-Je comprends les exercices qui utilisent le
théorème
|
1
|
2
|
3
|
4
|
5
|
6
|
|
de Thalès.
|
|
|
|
|
|
|
|
14-J'arrive à me motiver pour faire mes exercices sur
|
1
|
2
|
3
|
4
|
5
|
6
|
|
le théorème de Thalès.
|
|
|
|
|
|
|
|
15-Je suis capable de m'organiser pour faire mes
|
1
|
2
|
3
|
4
|
5
|
6
|
|
exercices sur le théorème de Thalès en
classe.
|
|
|
|
|
|
|
Feuille1
|
J'aime les mathématiques
|
L'histoire des mathématiques va me permettre d'apprendre
beaucoup de choses utiles.
|
Je fais des mathématiques pour obtenir une belle
récompense.
|
L'histoire des mathématiques m'intéresse
beaucoup.
|
J'ai choisi de faire de l'histoire des mathématiques pour
apprendre plein de choses.
|
Je fais de l'histoire des mathématiques pour faire plaisir
à mon enseignante.
|
Je fais des mathématiques pour faire plaisirs à mes
parents et à mon enseignante.
|
J'étudie l'histoire des mathématiques même
lorsque je ne suis pas obligé de le faire.
|
Dans la vie il est important d'apprendre à faire des
mathématiques.
|
Je fais des mathématiques pour montrer aux autres que je
suis bon.
|
Type de motivation de l'élève:
Intrinsèque, Extrinsèque ou Amotivation
Ext
Ext
Ext
A
Ext
Int-Ext Int
Int-Ext Int Ext Ext
Int-Ext Ext
Int-Ext Ext Ext Int Int Int
Élève 1
|
3
|
3
|
5
|
3
|
3
|
2
|
2
|
1
|
6
|
1
|
|
Élève 2
|
6
|
2
|
6
|
1
|
4
|
6
|
3
|
1
|
6
|
6
|
|
Élève 3
|
2
|
2
|
1
|
1
|
1
|
6
|
5
|
1
|
4
|
1
|
|
Élève 4
|
1
|
3
|
2
|
3
|
1
|
1
|
1
|
2
|
6
|
1
|
|
Élève 5
|
4
|
3
|
4
|
2
|
2
|
1
|
4
|
2
|
3
|
2
|
|
Élève 6
|
5
|
4
|
5
|
4
|
3
|
3
|
4
|
1
|
5
|
3
|
|
Élève 7
|
2
|
3
|
1
|
3
|
4
|
2
|
4
|
2
|
4
|
1
|
|
Élève 8
|
6
|
5
|
5
|
6
|
3
|
6
|
3
|
1
|
4
|
1
|
|
Élève 9
|
5
|
4
|
2
|
5
|
4
|
4
|
3
|
3
|
6
|
4
|
|
Élève 10
|
1
|
3
|
1
|
4
|
2
|
1
|
6
|
1
|
6
|
1
|
|
Élève 11
|
1
|
2
|
1
|
3
|
1
|
5
|
5
|
1
|
4
|
1
|
|
Élève 12
|
6
|
5
|
6
|
6
|
5
|
3
|
4
|
4
|
6
|
3
|
|
Élève 13
|
3
|
1
|
6
|
3
|
1
|
1
|
3
|
1
|
6
|
2
|
|
Élève 14
|
6
|
5
|
6
|
5
|
5
|
2
|
1
|
2
|
6
|
1
|
|
Élève 15
|
3
|
2
|
4
|
3
|
3
|
4
|
4
|
3
|
5
|
4
|
|
Élève 16
|
6
|
1
|
3
|
1
|
1
|
1
|
6
|
1
|
6
|
1
|
|
Élève 17
|
2
|
6
|
1
|
3
|
5
|
1
|
1
|
3
|
6
|
1
|
|
Élève 18
|
6
|
5
|
1
|
4
|
4
|
1
|
1
|
1
|
6
|
5
|
|
Élève 19
|
3
|
4
|
2
|
4
|
5
|
1
|
4
|
4
|
6
|
1
|
Page 1
Moy 3,7 3,3 3,3 3,4 3,0 2,7 3,4 1,8 5,3 2,1
|
motivation intrinsèque
|
Pourcentage motivation intrinsèque:
Pourcentage motivation extrinsèque: ge motivation
intrinsèque et extrinsèque: Pourcentage d'amotivation
:
|
26,3%
|
|
|
|
|
motivation extrinsèque
|
47,4 %
21,1 %
5%
|
Page 3
Feuille1
|
J'arrive toujours à finir les exercices sur le
théorème de Thalès.
|
J'arrive à me concentrer sur mes exercices sur le
théorème de Thalès en classe.
|
Je comprends les exercices qui utilisent le
théorème de Thalès.
|
J'arrive à me motiver pour faire mes exercices sur le
théorème de Thalès.
|
Je suis capable de m'organiser pour faire mes exercices sur le
théorème de Thalès en classe.
|
Moyenne élève Thalès
|
|
4
|
4
|
4
|
3
|
5
|
4,0
|
|
6
|
6
|
6
|
5
|
6
|
5,8
|
|
4
|
3
|
4
|
2
|
1
|
2,8
|
|
1
|
4
|
1
|
2
|
1
|
1,8
|
|
2
|
3
|
2
|
2
|
3
|
2,4
|
|
5
|
4
|
4
|
4
|
4
|
4,2
|
|
3
|
3
|
3
|
4
|
3
|
3,2
|
|
5
|
5
|
6
|
3
|
4
|
4,6
|
|
4
|
4
|
5
|
4
|
5
|
4,4
|
|
6
|
1
|
6
|
1
|
6
|
4,0
|
|
2
|
2
|
1
|
4
|
3
|
2,4
|
|
5
|
5
|
6
|
6
|
5
|
5,4
|
|
3
|
6
|
3
|
6
|
3
|
4,2
|
|
6
|
5
|
6
|
6
|
5
|
5,6
|
|
2
|
2
|
3
|
3
|
3
|
2,6
|
|
3
|
5
|
3
|
1
|
1
|
2,6
|
|
6
|
6
|
6
|
5
|
4
|
5,4
|
|
4
|
1
|
6
|
6
|
6
|
4,6
|
|
5
|
4
|
5
|
4
|
5
|
4,6
|
|
4,0
|
3,8
|
4,2
|
3,7
|
3,8
|
|
|
Moyenne Thalès:
|
3,9/6
|
Feuille1
|
Élève 1
|
4
|
4
|
1
|
3
|
1
|
1
|
2
|
1
|
4
|
4
|
|
Élève 2
|
1
|
5
|
2
|
3
|
1
|
1
|
1
|
1
|
6
|
2
|
|
Élève 3
|
1
|
2
|
1
|
1
|
1
|
6
|
6
|
1
|
6
|
2
|
|
Élève 4
|
6
|
3
|
2
|
4
|
2
|
3
|
4
|
1
|
5
|
5
|
|
Élève 5
|
1
|
3
|
1
|
4
|
1
|
1
|
1
|
1
|
5
|
1
|
|
Élève 6
|
5
|
3
|
1
|
3
|
2
|
1
|
2
|
4
|
6
|
2
|
|
Élève 7
|
3
|
5
|
2
|
1
|
2
|
6
|
6
|
1
|
4
|
3
|
|
Élève 8
|
4
|
4
|
2
|
2
|
2
|
5
|
5
|
2
|
4
|
1
|
|
Élève 9
|
4
|
4
|
3
|
2
|
3
|
1
|
1
|
3
|
6
|
4
|
|
Élève 10
|
5
|
4
|
1
|
6
|
4
|
1
|
1
|
4
|
5
|
4
|
|
Élève 11
|
2
|
3
|
1
|
1
|
1
|
4
|
4
|
1
|
2
|
1
|
|
Élève 12
|
4
|
2
|
1
|
3
|
3
|
4
|
3
|
2
|
4
|
4
|
|
Élève 13
|
6
|
6
|
6
|
1
|
6
|
1
|
1
|
1
|
6
|
1
|
|
Élève 14
|
5
|
6
|
2
|
5
|
6
|
1
|
1
|
4
|
6
|
1
|
|
Élève 15
|
6
|
4
|
2
|
4
|
4
|
2
|
1
|
1
|
5
|
1
|
|
Élève 16
|
5
|
3
|
1
|
4
|
1
|
2
|
3
|
2
|
5
|
3
|
|
Élève 17
|
3
|
2
|
5
|
2
|
2
|
2
|
4
|
2
|
6
|
1
|
|
Élève 18
|
5
|
2
|
3
|
2
|
3
|
1
|
1
|
1
|
3
|
3
|
|
Élève 19
|
6
|
4
|
2
|
4
|
4
|
4
|
4
|
4
|
5
|
1
|
Type de motivation de l'élève:
Intrinsèque, Extrinsèque ou Amotivation
|
J'aime les mathématiques
|
L'histoire des mathématiques va me permettre d'apprendre
beaucoup de choses utiles.
|
Je fais des mathématiques pour obtenir une belle
récompense.
|
L'histoire des mathématiques m'intéresse
beaucoup.
|
J'ai choisi de faire de l'histoire des mathématiques pour
apprendre plein de choses.
|
Je fais de l'histoire des mathématiques pour faire plaisir
à mon enseignante.
|
Je fais des mathématiques pour faire plaisirs à mes
parents et à mon enseignante.
|
J'étudie l'histoire des mathématiques même
lorsque je ne suis pas obligé de le faire.
|
Dans la vie il est important d'apprendre à faire des
mathématiques.
|
Je fais des mathématiques pour montrer aux autres que je
suis bon.
|
Int Int Ext Int-Ext
A
Int Ext Ext Int Int Ext
Int-Ext
Int-Ext Int Int Int Ext
A
Int-Ext
Page 1
Moy 4,0 3,6 2,1 2,9 2,6 2,5 2,7 1,9 4,9 2,3
|
motivation intrinsèque
|
Pourcentage motivation intrinsèque:
Pourcentage motivation extrinsèque: ge motivation
intrinsèque et extrinsèque: Pourcentage d'amotivation
:
|
42,1%
|
|
|
|
|
motivation extrinsèque
|
26,3%
21,1 %
11%
|
Page 3
Feuille1
|
J'arrive toujours à finir les exercices sur le
théorème de Thalès.
|
J'arrive à me concentrer sur mes exercices sur le
théorème de Thalès en classe.
|
Je comprends les exercices qui utilisent le
théorème de Thalès.
|
J'arrive à me motiver pour faire mes exercices sur le
théorème de Thalès.
|
Je suis capable de m'organiser pour faire mes exercices sur le
théorème de Thalès en classe.
|
Moyenne élève Thalès
|
|
4
|
3
|
3
|
2
|
2
|
2,8
|
|
3
|
3
|
4
|
4
|
3
|
3,4
|
|
4
|
3
|
3
|
1
|
1
|
2,4
|
|
5
|
6
|
6
|
6
|
4
|
5,4
|
|
3
|
2
|
2
|
1
|
6
|
2,8
|
|
1
|
1
|
1
|
1
|
1
|
1,0
|
|
6
|
6
|
4
|
4
|
6
|
5,2
|
|
4
|
2
|
2
|
2
|
1
|
2,2
|
|
4
|
4
|
4
|
2
|
3
|
3,4
|
|
4
|
2
|
2
|
1
|
1
|
2,0
|
|
5
|
4
|
4
|
2
|
3
|
3,6
|
|
5
|
4
|
5
|
4
|
4
|
4,4
|
|
6
|
6
|
6
|
6
|
6
|
6,0
|
|
5
|
6
|
6
|
6
|
6
|
5,8
|
|
5
|
5
|
5
|
5
|
5
|
5,0
|
|
5
|
4
|
5
|
3
|
5
|
4,4
|
|
5
|
6
|
6
|
5
|
6
|
5,6
|
|
5
|
5
|
6
|
4
|
3
|
4,6
|
|
5
|
5
|
5
|
5
|
5
|
5,0
|
|
4,4
|
4,1
|
4,2
|
3,4
|
3,7
|
|
|
Moyenne Thalès:
|
3,9/6
|
Feuille1
|
Élève 1
|
5
|
4
|
4
|
3
|
4
|
4
|
2
|
2
|
4
|
3
|
|
Élève 2
|
5
|
6
|
1
|
6
|
6
|
1
|
1
|
3
|
6
|
1
|
|
Élève 3
|
4
|
3
|
3
|
4
|
5
|
1
|
1
|
1
|
6
|
3
|
|
Élève 4
|
5
|
2
|
3
|
1
|
4
|
2
|
2
|
1
|
5
|
2
|
|
Élève 5
|
4
|
1
|
5
|
1
|
1
|
3
|
4
|
1
|
6
|
1
|
|
Élève 6
|
5
|
4
|
4
|
3
|
3
|
6
|
4
|
1
|
4
|
1
|
|
Élève 7
|
1
|
1
|
1
|
2
|
1
|
1
|
3
|
1
|
6
|
3
|
|
Élève 8
|
4
|
5
|
4
|
2
|
4
|
1
|
5
|
1
|
6
|
1
|
|
Élève 9
|
4
|
6
|
5
|
4
|
5
|
4
|
3
|
4
|
6
|
4
|
|
Élève 10
|
5
|
2
|
3
|
4
|
4
|
1
|
1
|
2
|
6
|
1
|
|
Élève 11
|
1
|
2
|
6
|
1
|
1
|
1
|
6
|
1
|
2
|
1
|
|
Élève 12
|
4
|
2
|
4
|
2
|
2
|
2
|
2
|
2
|
6
|
2
|
|
Élève 13
|
3
|
3
|
1
|
2
|
4
|
2
|
1
|
1
|
5
|
1
|
|
Élève 14
|
5
|
2
|
2
|
1
|
4
|
1
|
1
|
4
|
6
|
4
|
|
Élève 15
|
1
|
1
|
2
|
1
|
4
|
1
|
5
|
1
|
2
|
1
|
|
Élève 16
|
2
|
4
|
4
|
2
|
3
|
1
|
5
|
6
|
5
|
1
|
|
Élève 17
|
3
|
4
|
6
|
3
|
3
|
3
|
4
|
2
|
5
|
3
|
|
Élève 18
|
3
|
1
|
1
|
3
|
2
|
2
|
2
|
1
|
5
|
2
|
|
Élève 19
|
4
|
5
|
5
|
3
|
2
|
1
|
1
|
2
|
6
|
1
|
|
Élève 20
|
2
|
1
|
3
|
2
|
3
|
2
|
2
|
1
|
4
|
2
|
|
Élève 21
|
6
|
5
|
5
|
4
|
4
|
2
|
1
|
4
|
5
|
2
|
|
Élève 22
|
5
|
1
|
3
|
1
|
1
|
1
|
1
|
1
|
6
|
1
|
|
Élève 23
|
5
|
4
|
4
|
3
|
3
|
3
|
4
|
2
|
6
|
5
|
|
Élève 24
|
3
|
4
|
2
|
2
|
3
|
4
|
1
|
4
|
5
|
2
|
|
Élève 25
|
3
|
1
|
4
|
3
|
4
|
3
|
6
|
1
|
6
|
6
|
|
Élève 26
|
5
|
3
|
1
|
4
|
3
|
4
|
2
|
2
|
1
|
1
|
Type de motivation de l'élève:
Intrinsèque, Extrinsèque ou Amotivation
|
J'aime les mathématiques
|
L'histoire des mathématiques va me permettre d'apprendre
beaucoup de choses utiles.
|
Je fais des mathématiques pour obtenir une belle
récompense.
|
L'histoire des mathématiques m'intéresse
beaucoup.
|
J'ai choisi de faire de l'histoire des mathématiques pour
apprendre plein de choses.
|
Je fais de l'histoire des mathématiques pour faire plaisir
à mon enseignante.
|
Je fais des mathématiques pour faire plaisirs à mes
parents et à mon enseignante.
|
J'étudie l'histoire des mathématiques même
lorsque je ne suis pas obligé de le faire.
|
Dans la vie il est important d'apprendre à faire des
mathématiques.
|
Je fais des mathématiques pour montrer aux autres que je
suis bon.
|
Int-Ext*
Int
Int
Int
Int-Ext*
Int-Ext
A
Int-Ext
Int-Ext
Int
Ext
Int-Ext
Int*
Int
Ext
Int-Ext
Int-Ext
Int
Int-Ext
A
Int-Ext
Int Int-Ext Int-Ext
Ext
Int-Ext
Moy 3,7 3,0 3,3 2,6 3,2 2,2 2,7 2,0 5,0 2,1
motivation intrinsèque motivation extrinsèque
élève orateur
30,4%
13,0%
47,8 %
9 % * : ne compte pas
Page 1
Pourcentage motivation intrinsèque: Pourcentage
motivation extrinsèque: ge motivation intrinsèque et
extrinsèque:
Pourcentage d'amotivation :
Feuille1
J'arrive toujours à finir les exercices sur le
théorème de Thalès.
J'arrive à me concentrer sur mes exercices sur le
théorème de Thalès en classe.
Je comprends les exercices qui utilisent le
théorème de Thalès.
J'arrive à me motiver pour faire mes exercices sur le
théorème de Thalès.
Je suis capable de m'organiser pour faire mes exercices sur le
théorème de Thalès en classe.
Moyenne élèves exposés
Thalès
Moyenne autres élèves
Thalès
Page 3
3
|
4
|
4
|
4
|
4
|
3,8
|
|
|
3
|
6
|
4
|
5
|
6
|
|
4,8
|
|
5
|
5
|
4
|
5
|
4
|
|
4,6
|
|
5
|
5
|
6
|
3
|
5
|
|
4,8
|
|
5
|
6
|
6
|
4
|
4
|
5
|
|
|
4
|
4
|
4
|
3
|
4
|
|
3,8
|
|
1
|
5
|
5
|
4
|
5
|
|
4,0
|
|
4
|
1
|
2
|
3
|
3
|
|
2,6
|
|
3
|
5
|
4
|
4
|
3
|
|
3,8
|
|
6
|
5
|
6
|
4
|
6
|
|
5,4
|
|
1
|
1
|
1
|
1
|
1
|
|
1,0
|
|
5
|
5
|
6
|
4
|
6
|
|
5,2
|
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
6
|
5
|
6
|
1
|
6
|
|
4,8
|
|
6
|
4
|
5
|
5
|
4
|
|
4,8
|
|
5
|
4
|
5
|
4
|
5
|
|
4,6
|
|
2
|
3
|
4
|
4
|
4
|
|
3,4
|
|
4
|
4
|
5
|
4
|
3
|
|
4,0
|
|
3
|
2
|
3
|
5
|
5
|
|
3,6
|
|
1
|
1
|
1
|
2
|
2
|
|
1,4
|
|
5
|
6
|
5
|
6
|
6
|
|
5,6
|
|
5
|
5
|
6
|
3
|
5
|
|
4,8
|
|
3
|
5
|
4
|
3
|
3
|
|
3,6
|
|
3
|
5
|
4
|
3
|
4
|
|
3,8
|
|
2
|
4
|
4
|
5
|
5
|
|
4,0
|
|
5
|
6
|
5
|
4
|
6
|
|
5,2
|
|
3,7
|
4,1
|
4,2
|
3,6
|
4,2
|
|
|
|
Moyenne Thalès:
|
4,1/6
|
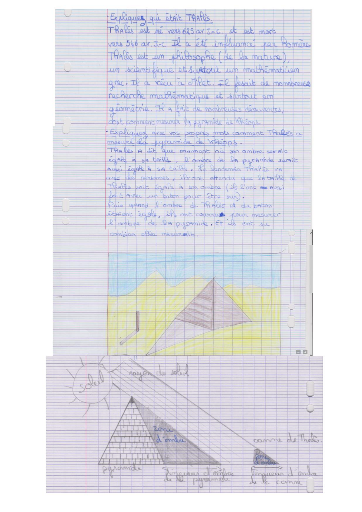
Résumé
Notre étude a pour objectif de montrer
l'efficacité possible de l'introduction de l'Histoire des
Mathématiques au collège sur la motivation des
élèves et leurs résultats.
Avant de faire nos propres expérimentations, une partie
« état de l'art » dresse le bilan des études
déjà menées, des arguments en faveur ou contre
l'introduction historique des Mathématiques, et enfin présente
les différents types de motivation.
Dans un premier temps, l'acquisition des compétences de
deux classes de 4ème ont été comparées
sur la séquence « Equations » : l'une a
bénéficié d'une introduction historique, l'autre plus
classique. Cette expérimentation a permis de mettre en avant
l'efficacité de l'Histoire sur l'acquisition des connaissances
Mathématiques.
Dans un second temps, trois expérimentations sur la
séquence du théorème de Thalès
(4ème) ont été réalisées dans
trois classes différentes. Il s'agissait d'associer à chaque type
d'activité le type de motivation sur lequel elle influait le plus et
avec quelle intensité.
L'évaluation de la motivation s'est faite grâce
à un questionnaire permettant de définir pour chaque
élève son profil motivationnel et son Sentiment
d'Efficacité Personnelle.
L'analyse des résultats a permis d'observer que
l'utilisation de l'Histoire des Mathématiques par approche historique
intégrée influait principalement sur la motivation
extrinsèque, que l'approche par module d'apprentissage agissait à
la fois sur la motivation extrinsèque et intrinsèque, et qu'enfin
l'approche anecdotique conduisait à une motivation intrinsèque.
Les trois types de démarches semblent en revanche toutes aussi
efficaces.
Mots-clés : Histoire des
Mathématiques en classe, évaluation de la motivation, Sentiment
d'Efficacité Personnelle, 4ème
Summary
The objective of our study is to show the potential efficiency
of the introduction of the History of Mathematics at college level (France) on
the pupils' motivation and their school results.
The first part of our production shows the results which have
already been found by researchers in this field, and the pros and cons of a
historical introduction of Mathematics. Moreover, we present the different
kinds of motivation.
First, the acquisition of competences of two classes has been
compared on the chapter « Equations » : this notion has been
introduced in a historic way in the first class, and more traditionally in the
second. These experimentations showed us the efficiency of History in achieving
Mathematics skills.
In a second time, we conducted three experimentations on
Thales chapter in three different classes at the same level. We associated each
kind of activity with a motivation type, and we assessed its intensity.
That last assessment has been done thanks to a questionnaire
which permitted us to define for each pupil his kind of motivation and his
Sense of Self-Efficacy.
The analysis of the results shows that using History of
Mathematics with history-based approach particularly influences intrinsic
motivation whereas a module approach influences as much an extrinsic as
intrinsic motivation, and finally an illumination approach has a more important
effect on only intrinsic motivation. The three kinds of activity seem to be
equally effective.
Keywords : History of Mathematics in class,
assessing motivation, Sense of Self-Efficacy, college (4ème,
France)
| 


