|
EPIGRAPHE
Les gens heureux ne perdent pas de temps à faire du
mal aux autres. La méchanceté appartient aux malheureux et aux
jaloux.
Malek Bensafia
IN
MEMORIAM
Ma très chère mère
Aimé-Marie MUSO KIKOKO qui nous a financé et qui
souhaitait nous voir terminer nos études mais Dieu n'a pas voulu en
l'appelant dans le royaume de cieux ;
Notre Ami Hyacinthe KIMBAMFU MUPENDE qui
ne fût pas qu'un ami mais aussi un frère, un conseillé dans
le domaine spirituel, un grand motivateur dans le domaine de l'informatique et
il nous suffit de signaler que si nous travaillons sur ce sujet, c'est
grâce à ses encouragements.
DEDICACE
Au Seigneur Jésus-Christ, source de
toute mon inspiration ;
A nom père Gibert FREY OYEY, au
Professeur Nestor ANZOLA KIBAMBA et à tous ceux
qui, d'une quelconque manière, ont contribué à
l'élaboration de ce travail. C'est à vous que je le
dédie.
REMERCIEMENTS
Au terme de ce travail qui sanctionne la fin de nos
études de licence en sciences informatiques à l'Université
de Kinshasa, nous ne pouvons conclure sans remercier de près ou de loin
tous ceux qui ont contribués à la concrétisation de ce
travail.
De prime à bord, nous remercions le Très-Haut,
Dieu Tout-puissant, lui qui demeure le commencement et la fin de toute chose.
Qu'il agrée l'expression de notre profonde gratitude !
Nous tenons à témoigner notre très haute
considération et gratitude, singulièrement au Professeur
Pierre KAFUNDA KATALAY qui, en dépit de ses multiples
occupations, a accepté d'assurer la direction de notre travail.
Nous manifestons notre expression de reconnaissance à
l'égard du Corps Professoral et Scientifique de la Faculté des
Sciences de l'Université de Kinshasa en général et celui
du Département de Mathématiques et informatique en particulier.
Je remercie très particulièrement mon
Père Gilbert FREY OYEY et le Professeur Nestor
ANZOLA qui malgré leurs occupations nous ont vraiment
orienté et qui continuent à nous orienter vers le vrai chemin de
la science.
Nos remerciements s'adressent également à
l'assistant AndréMUSAS et Tege SIMBONI, pour leurs
disponibilités et leurs conseils pertinents en vue de notre
orientation.
Mes remerciements vont à l'égard des membres de
la famille, à nos amis, frères et soeurs.
LISTE DES ABREVIATIONS
|
ABREVIATIONS
|
EXPLICATIONS
|
|
2D
|
Deux Dimension
|
|
3D
|
Trois Dimension
|
|
B-Rep
|
Représentation par Frontières (Boundary
Representation)
|
|
CAO
|
Conception Assisté par Ordinateur
|
|
COM
|
Component Object Model (objet composant modèle)
|
|
CSG
|
Géométrie Constructive des Solides (Constructive
Solid Geometry)
|
|
HAL
|
Hardware Abstraction Layer (Couche d'Abstraction
Matérielle)
|
|
HEL
|
Hardware Emulation Layer (Couche d'Emulation
Matérielle)
|
|
LMB
|
Left Mouse Button
|
|
MMB
|
Middle Mouse Button
|
|
NURBS
|
Spline Basique Rationnelle Non Uniforme (Non Uniform Rational
Basic Spline)
|
|
OpenGL
|
Open Graphics Library (bibliothèque graphique
overte)
|
|
PCI
|
Interconnexion de Composants Périphérique
(Peripheral Component Interconnect)
|
|
RepRap
|
Réplication Rapid Prototyper
|
|
RMB
|
Right Mouse Button
|
|
SLA
|
StéréoLithographie Apparatus
|
|
TIC
|
Technologie d'Information et de Communication
|
LISTE DES FIGURES
Figure I.1 : Représentation du moteur 3D (page
8)
Figure II.1: Polygone convexe rempli (page 23)
Figure II.2: Polygone convexe (page 24)
Figure II.3: Polygone quelconque (page 24)
Figure II.4: Ensemble de droites de la zone de clipping (page
25)
Figure II.5: Résultat (page 25)
Figure II.6 : Exemple du produit de DirectX (page 32)
Figure II.7: Exemple de l'image produit grâce à
OpenGL (page 34)
Figure II .8: Image produit par le moteur de Quake(page
34)
Figure II.9 : Abstraction entre les bibliothèques
3D (page 35)
Figure II.10 : Exemple du rendu produit par Java3D (page
36)
Figure III.1 : Modèle Darwin (imprimante 3D) (page
46)
Figure III.2 : Mandel Impriment (imprimante 3D) (page
47)
Figure III.3 : Modèle Huxley (imprimante 3D) (page
47)
Figure III.4 : Modèle Wallace (imprimante 3D)
(page 47)
Figure III.5 : Rostock (imprimante 3D) (page 48)
Figure III.6 : Hypercube (imprimante 3D) (page 48)
Figure IV.1 : Comparaison entre les interfaces de Blender
2 .49b et Blender 2 .5x et suivants. (Page 51)
Figure IV.2 : Scène de base fournie par Blender au
démarrage du logiciel (page 52).
Figure IV.3 : Sélecteur des différents modules
se trouvant dans chaque bloc (page53)
Figure IV.4. Etapes de modélisation de la
prothèse (page 56)
Figure IV.6. Visualisation de la prothèse en mode
Edite. (Page 57)
Figure IV.7. Visualisation de la prothèse en mode
Objet. (Page 57)
Figure IV.8. Vue de face de la prothèse. (Page 58)
Figure IV.9. Vue Interne de la prothèse. (Page 58)
Figure IV.10. Vue finale de la prothèse en mode Edition
sous format 2D (page 59)
Figure IV.11. Vue finale de la prothèse en mode Object
sous format 2D (page 60)
Figure IV.12. Vue finale de la prothèse en mode Object
sous format 3D (page 60)
Figure IV.13. Vue sur le plateau d'impression (page 61)
LISTE DES TRABLEAUX
Tableau I.1. Logiciels de modélisation 3D
Tableau II.1. Tableau de comparaison clipping 2D et 3D
INTRODUCTION GENERALE
L'informatique en tant que discipline scientifique et
technique s'est déployées sur deux siècles environs :
le 19ème et le 20ème siècle. Elle
est liée à l'apparition des premiers automates et à la
mécanisation d'un processus de développement et de
généralisation des machines qui a commencé au
18ème siècle en Europe avec l'industrialisation.
Depuis ces années jusqu'à nos jours, il a connu
des divers avancés comme : l'arrivé du terme robotique vers
1942, l'apparition de l'intelligence artificielle celle-ci a
débuté dans les années 1950 avec les travaux d'Alan Turing
qui se demandait si une machine pouvait penser.
1. PROBLEMATIQUE
Avec les progrès réalisés par les
Technologies de l'Information et de la
Communication (TIC), dans tous les secteurs
d'activités humaines ont permis certaines entreprises, d'adapter leur
solution informatique à d'autres réalités de la vie
surtout aux personnes vivant avec handicap.
Aujourd'hui avec l'évolution de la modernité,
une personne ayant perdu l'une des parties de son corps ne peut plus
désespérer du fait qu'on cherche à lui trouver une partie
similaire à celle perdue afin que ce dernier retrouve l'équilibre
et le sourire. Pour bien élaborer notre travail, nous nous sommes
posé quelques questions à savoir :
ü Comment aider nos frères à retrouver un
de leur membre amputé?
ü Est-il possible de mettre en place un objet
remplaçant un membre estropier de leur corps ?
2. HYPOTHESE
Se référant aux questions posées à
la problématique et vu sa pertinence, la solution proposée est
celle de mettre en place un système de modélisation des
prothèses 3D. Ce système 3D (modélisation 3D) permettra
à ce que chaque personne puisse retrouver sourire par apport à
l'une des parties de son corps perdu.
Ce dernier est vraiment très avantageux, car il va
donner de l'équilibre à ces personnes.
3. INTERET DU SUJET
L'intérêt de ce travail est d'aider des personnes
vivant avec handicap à retrouver un membre perdu lors d'un accident,
d'un affrontement armé et autres. C'est à travers ce
système 3D ; que les personnes ayant perdu un membre du corps
humain pourront les retrouver imprimés en 3D.
4. DELIMITATION DU SUJET
Aujourd'hui, il existe de nombreuses prothèses
permettant de remplacer un membre. Nous distinguons plusieurs types de
prothèses : Prothèse articulaire, prothèse oculaires,
prothèse de dentaires, prothèse du coeur, prothèse de la
main, prothèse du genou, etc.
Dans ce travail, nous allons extraire de connaissances sur la
prothèse de la main pour permettre aux personnes qui ont des
problèmes avec leur main, de la retrouver imprimé en 3D.
5. METHODES ET TECHNIQUES
UTILISEES
a. Méthode
Pour ce travail, plusieurs méthodes nous ont beaucoup
aidé. Nous pouvons citer : 3DSizeME, 3D Creator, Bevel, Canvas,
itSeez3D, Qlone, SketchUp, Blender, etc.
Ces méthodes sont directement liées aux
logiciels portent les mêmes noms que les logiciels de modélisation
et d'impression 3D.
b. Technique
utilisées :
Ø La Technique d'interview
Elle nous a permis d'échanger avec le public en se
référant aux questions écrites pour avoir des informations
sûres.
Ø Technique documentaire
Nous avons consulté des ouvrages et publications
d'autres personnes ayant abordé ce sujet dans le même contexte que
nous ; et nous avons consulté le laboratoire fabLab pour la partie
pratique de notre sujet.
6. SUBDIVISION DU TRAVAIL
Hormis l'introduction générale et la conclusion
générale, notre travail se subdivise en quatre chapitres,
à savoir :
CHAP 1 : GENERALITE SUR LA MODELISATION 3D
CHAP 2 : PROGRAMMATION 3D
CHAP 3 : ETUDE DE SYSTEME D'IMPRESSION 3D
CHAP 4 : REALISATION DE LA PROTHESE EN 3D
Chap I.
Généralité sur la Modélisation 3D
[1,2,3,8,9]
I.0. Introduction [9]
La modélisation tridimensionnelle est
l'étape en infographie tridimensionnelle qui consiste à
créer, dans un logiciel de modélisation 3D, un objet en trois
dimensions, par ajout, soustraction et modifications de ses constituants.
Dans ce chapitre, nous allons éclaircir c'est quoi
l'infographie et donner les notions préliminaires sur la
modélisation 3D. A la suite, nous allons expliquer ou montrer en long et
en large comment cette modélisation se réalise. Elle est en soi
une technique majoritairement utilisée dans le jeu vidéo, la
médecine interne ou externe et le cinéma d'animation.
I.1. Infographie 3D [9]
L'infographie trois dimension, souvent abrégée
Infographie3D est un ensemble de techniques notamment issues
de la conception assistée par ordinateur (
CAO)
qui permet la représentation d'objets en
perspectivesur
un moniteur d'ordinateur.
Grace à cette infographie, on peut faire la
synthèse tridimensionnelle et par là, on fait
référence à l'espace vectoriel. Sa décomposition
fait appelle à trois dimensions cartésiens qu'on peut nommer x, y
et z.
Prenons, dans une pièce, un point de
référence, et définissons des directions gauche-droite
(X), avant-arrière (Y) et haut-bas (Z). Pour aller de l'origine à
un point donné, il faut faire : x (mètres vers la droite),
y(mètres vers l'avant), z (mètres vers le haut).
I.2. Modèle
Numérique ou Modélisation 3D [1,2,5,9]
Comme on l'a dit précédemment, le modèle
numérique autrement dit modélisation en trois dimensions est une
représentation numérique d'un objet. Et dans le 3D, On
s'intéresse aux modèles numériques représentant des
objets physiques.
y
Cette modélisation 3D est issue de l'infographie trois
dimension. Elle est actuellement très utilisée en
artnumérique
dans l'industrie du film, initiée par les studios
Pixar,
Disney,
DreamWorks,
BlueSky,
Illumination
et
ILM et,
depuis
1992, dans beaucoup de
jeuxvidéo.
Faisant référence à 3D, on a donc trois axes x, y et z qui
constituent le repère orthonormé de la géométrie
y
d'espace.
x
z
En effet, la synthèse des images 3D se décompose
essentiellement en deux étapes à savoir :
ü Modélisation : c'est
l'étape qui consiste à modéliser ce que l'on veut
visualiser ou représenter ;
ü Rendu : il consiste à
effectuer la visualisation de ce que l'on a modélisé.
I.2.1. Modélisation
[1,5,9]
En parlant de la modélisation, on fait
référence au stockage par l'ordinateur d'un ensemble de
données géométriques et de caractéristiques
graphiques permettant de représenter ensuite le modèle. Ce
modèle est habituellement appelé scène 3D, d'après
l'anglais scène qui signifie « vue ».
a. Méthode de
Modélisation
Nous avons plusieurs méthodes de modélisation
à savoir : B-Rep, CSG,
Splines et Surfaces implicites.
1. CSG (Constructive Solid Geometry,
géométrie constructive des solides) : la définition
des objets est fait grâce aux opérations (unions,
intersections...) sur des formes géométriques dans l'espace
(polyèdres, sphères, cônes, courbes de Bézier,
splines, NURBS...).
2. B-Rep (Boundary Representation,
représentation par frontières) : la limite de chaque objet
est faite à partir des formes géométriques 2D
(généralement des triangles). C'est le format naturel de sortie
des scanners 3D qui mesurent les cotes de points à la surface des
objets. C'est aussi la représentation généralement
utilisée par les dispositifs d'affichage accélérés
pour la 3D.
3. Splines : c'est làoù
les surfaces sont décrites par des courbes formant un treillis.
4. Surfaces Implicites, où les objets
à représenter sont décrits par des surfaces joignant des
volumes, le plus souvent des sphères.
b. Contraintes temporelles dans la
modélisation [5,9]
Partant du contrainte temps, la modélisation se
réalise suivant un temps précis à savoir :
ü La Modélisation temps réel ;
ü La Modélisation
précalculé ;
ü La Modélisation hybride.
1. La modélisation temps Réel
La modélisation temps réel est souvent
utilisé dans le jeux vidéo, mais a également de nombreuses
autres applications : visualisation architecturale, visualisation
médicale, simulations diverses, économiseurs
d'écrans...
Dans l'ancien temps, tous les calculs revenaient au processeur
central (CPU) des ordinateurs, mais la puissance toujours plus grande
demandée pour améliorer la qualité des images poussant des
constructeurs à commercialiser des cartes PCI (Peripheral Component
Interconnect) spécialisées dans la 3D.
Il suffit à noter que : Le
smartphoneSamsung Galaxy S7 a été le premier
appareil mobile à proposer l'accès à l'API Vulkan, et la
démonstration qui a été faite utilisant le moteur
3D ; Unreal Engine4 a repoussé les limites de la
modélisation temps réel sur mobile. En suite les tablettes
AndroidNvidia Shield ont également été mises à jour
avec le support de Vulkan.
2. La Modélisation Pré-calculée
La Modélisation pré-calculée est
utilisée dans la création d'images, d'effets spéciaux et
de films d'animation. Son avantage principal est qu'elle permet d'obtenir une
très grande qualité d'image et un réalisme poussé.
L'image est qualifiée de « photoréalisme »
lorsque son niveau de détail est très important. On peut alors la
confondre avec une photographie.
Une préoccupation pour les temps de calcul existe, mais
à une échelle totalement différente de celle de la
modélisation temps réel. En effet, dans cette dernière,
une animation fluide demande qu'il soit possible de calculer plus de vingt
images par seconde, alors avec la
modélisationpré-calculée, le calcul d'une image peut
prendre des heures, voire des jours.
3. La Modélisation Hybride
La Modélisation hybride vise à améliorer
le photoréalisme de la modélisation temps réel en
pré-calculée. Certains paramètres dont le calcul est
coûteux mais dont la qualité est indispensable au réalisme
de l'image.
L'éclairage fait partie de ces paramètres
coûteux. Et en modélisation temps réel, il est
sacrifié : pas ou peu d'ombres portées, pas d'illumination
globale. Or, un bon éclairage apporte énormément au
réalisme de l'image et c'est souvent ce qui fait la grande
différence entre la modélisation temps réel et la
modélisation pré-calculée.
En utilisant l'application de modélisation 3D, on doit
se mettre en tête qu'elle doit respecter certaines contraintes : de
foi il peut se faire avec contrainte physique ou sans contrainte physique.
1. Avec contraintes physiques :
En tenant compte de la modélisation avec contrainte
physique, on voit son importance dans plusieurs domaines de la vie
humaine : médecine, architecture, mécanique et Urbanisation.
ü Médecine : ça aide
à la confection de prothèses, reconstruction d'organes etc.
ü Architecture : ça aide à
la visualisation de futurs bâtiments, insertion de bâtiments dans
le paysage etc.
ü Mécanique : ça aide
à faire de simulation physique d'entraînement d'engrenage, tests
de montage, usinage de pièces etc.
ü Urbanisme : ça aide à
faire de simulation de circulation etc.
2. Sans contrainte physique :
Ici on effectue la modélisation de personnages, animaux
etc. de façon réaliste, avec effets spéciaux,
éclairage, rendu plausible des images pour satisfaire l'oeil des
spectateurs.
Pour se faire, la modélisation sans contrainte
physique, s'applique dans :
ü Cinéma ;
ü Jeux vidéo ;
I.2.2. Rendu
Le rendu est une phase qui consiste à transformer
l'espace 3D en une image 2D. Le rendu est généré par un ou
des programme(s) qu'on appelle moteur de rendu 3D, intégré(s) ou
non au logiciel de modélisation.
Monteur De Rendu
Le moteur de rendu, est un logiciel ou un programme
intégré à un logiciel de modélisation qui permet la
transformation de l'univers 3D à l'univers 2D (écran) !

Figure I.1 : Représentation du moteur
3D
Le rendu est constitué de plusieurs phases :
ü Calcul de l'éclairage (on parle
d'illumination) ;
ü Projection dans le plan d'observation. ;
ü Dessin à proprement parler avec application
éventuelle de
textures.
Il se peut que certaines de ces phases soient
réalisées en même temps (dans les cartes 3D par
exemple).
Calcul de l'éclairage
1. Calcul de l'éclairage locale
ü L'
algorithme de
Gouraud, est une
méthode de rendu très simplifiée puisqu'elle consiste
à interpoler sur l'image en 2D, ligne par ligne au niveau des pixels,
les valeurs d'intensité de l'intérieur d'un
polyèdreselon
les intensités de ses voisins : c'est un lissage 2D.
ü L'
algorithme de
Phong est un ombrage
3D qui permet d'avoir un volume et un effet de matière, en fonction de
la source de lumière et de propriété de
réflexion
de la lumière du matériau en chaque point du
polyèdre, par
interpolation des normales aux sommets.
2. Calcul de l'éclairage locale
La
radiosité
calcule les échanges d'énergie lumineuse entre
éléments de surface de la scène en tenant compte de leurs
propriétés de
réflexionet
d'
absorption.
Cela nécessite de décomposer la scène en
élémentsfinis
de surface. Cela permet des éclairages naturellement doux. Cette
technique associée au lancer de rayons et à d'autres voisines
permettant les inter-réflexions est une technique d'
illuminationglobale.
Projection
Les objets ainsi définis par des nombres peuvent
ensuite être dessinés sur un écran ; les triplets de
valeurs (x, y, z) sont transformés en points du dessin. Ce rendu utilise
généralement la notion de
Perspectivelinéaire :
plus l'objet est loin, plus il est dessiné petit ; ce
procédé est parfois qualifié de « vraie
3D » ou de « vision naturelle ».
La position des points s'obtient facilement. Un
produitmatricieleffectue
un changement de coordonnées, vers un
repère
dont l'origine est le point de vue, l'axe de profondeur z' est la direction
principale, perpendiculaire à la surface de rendu, et les deux autres
axes, x' et y' sont parallèles à la largeur et la hauteur de la
surface de rendu. Un produit scalaire par le quotient de la distance entre
point de vue et surface de rendu et la cote sur l'axe z' de profondeur,
ramène ensuite tous les points dans le plan de visualisation.
La
perspectiveaxonométrique,
dont la
perspectivecavalière
et les
projectionsorthogonales
(notamment la
perspectiveisométrique,
voir aussi
Géométriedescriptive)
est une perspective linéaire pour une distance d'observation infinie. La
taille de l'objet ne varie pas avec l'éloignement ;
l'éloignement est figuré par un déplacement dans le plan
de la figure. Elle s'obtient également par calcul matriciel.
Le rendu doit généralement déterminer
quelles sont les parties visibles et les parties cachées. Les techniques
de la synthèse d'images 3D ont d'abord distingué les algorithmes
de calcul des faces cachées qui travaillaient dans
l'espace 3D de la scène et ceux du rendu
photoréalismequi travaillaient dans l'espace 2D de l'image
(pixels). Les algorithmes de rendu actuels réalisent les deux fonctions
simultanément.
D'autres algorithmes de rendu tiennent compte du fait que les
détails et les contrastes s'estompent avec l'éloignement (
perspectiveatmosphérique).
Dessin
À ces types de perspective, on associe un type de
dessin :
ü
Z-buffer (tampon de profondeur des pixels), utilisant l'
algorithmedit du
peintre (qui peint la scène en partant du fond puis successivement les
sujets de plus en plus rapprochés) pour afficher les scènes
constituées de polygones ou de structures plus évoluées
comme les
nurbs, et qui gère
correctement l'affichage de polygones entremêlés à la
précision de l'affichage car le tracé se fait pixel par pixel.
C'est une méthode 3D de calcul de faces cachées à
l'échelle des pixels car elle conserve la profondeur de chaque pixel.
ü Le
lancerderayon
(raytracing, dont est dérivé le
raycasting), simulant le
parcours inverse de la lumière de la scène vers l'oeil. Cette
technique permet de simuler relativement facilement les
phénomènes physiques que sont
réflexion et
réfraction ainsi que
les ombres portées mais crée des scènes trop pures et
irréalistes. Dans ce cas, la projection est réalisée en
même temps que le dessin car tracer un rayon implique de le projeter dans
la scène 3D.
ü Autres.
I.3. Quelques types de
modélisation 3D [8]
Il existe plusieurs types de modélisation 3D à
savoir :
I.3.1. Modélisation
à partir d'exemples
Les méthodes de modélisation à partir
d'exemples permet de réutiliser des modèles existant, et de
construire un modèle existant par assemblage. Contrairement à la
géométrie de construction de solides, les primitives ne sont pas
des objets géométriques simples (cône, cylindre, cube,
etc.) mais des sous-partie de polyèdres. Le résultat final est
donc un polyèdre, et la surface ainsi obtenue peut-être une
variété, ou non.
Les méthodes de modélisation à partir
d'exemples font appel à des algorithmes de recherche au sein d'une base
de données de modèle 3D et d'assemblage de maillage.
a. Avantage
ü La modélisation à partir d'exemple permet
de créer des polyèdres donc les algorithmes de rendu pour ce type
de données sont toujours adaptés.
ü Le temps de création d'un modèle 3D est
réduit, puisque le maillage final est obtenu par assemblage de maillages
existant.
ü Le processus de modélisation est aussi
simplifié, ce qui permet à un plus grand nombre d'utilisateurs de
créer des données 3D.
b. Inconvénients
ü De manière analogue à
l'échantillonnage en musique, la réutilisation de données
existantes pose des questions en matière de propriété
intellectuelle et de copyright.
ü La qualité des maillages obtenus est directement
dépendante du matériau de base, notamment en matière de
résolution et de topologie.
I.3.2. Modélisation par
courbes (NURBS)
La modélisation par NURBS (Non uniform
rational basic spline/Spline basique rationnelle non uniforme) consiste en un
réseau de courbes créé grâce à des points de
contrôles (control vertices). L'interpolation des courbes entre ces
points peut se faire automatiquement selon un algorithme NURBS, par la
manipulation de tangentes de
courbedeBézier,
ou encore par modification des paramètres d'interpolation.
La modélisation par courbe se base sur un maillage
adaptatif, conçu pour adapter ses subdivisions à la
complexité des courbes dans une région donnée. Une surface
parfaitement plane aura un nombre de subdivision très faible ou nul.
C'est la technique de modélisation la plus précise. C'est la
raison pour laquelle elle est massivement utilisée en architecture et en
CAOindustrielle,
lorsque le souci de précision prime (notamment lorsque les
modèles 3D servent de référence pour les machines-outils).
I.3.3. Modélisation par
subdivision de surface
Cette méthode regroupe deux méthodes classiques
(polygonale et NURBS). Elle consiste à accélérer le
processus grâce à la subdivision automatique d'une partie de la
surface. Ceci permet d'ajouter des détails à certains endroits
uniquement, sans se soucier du nombre de faces comprises sur la
globalité de l'objet.
Elle se rapproche de la modélisation polygonale par les
techniques employées lors de la création de la forme, et de la
modélisation par NURBS en ce qui concerne le rendu de la surface,
c'est-à-dire son arrondi.
Elle est présente dans de nombreux logiciels
professionnels (Blender, Maya, 3ds Max, Lightwave, Softimage, Modo...).
I.3.4. Modélisation de
construction de solides
En infographie, la modélisation de construction de
solides n'est rien d'autre que la géométrie de
construction de solides (CSG en anglais: "Constructive Solid
Geometry") qui est juste une branche de la modélisation des solides.
La modélisation géométrique des solides
procède deux méthodes :
ü La CSG (dite aussi
"modélisation solide" ou "modélisation volumique"),
ü La B-Rep ("Boundary
Représentation" dite aussi "modélisation surfacique").
a. Avantages
La géométrie de construction de solides permet
d'accélérer les calculs qui peuvent se baser sur des volumes
plutôt que sur les polygones.
ü Cette méthode de modélisation est assez
adaptée au lancer de rayon car ce dernier travaille principalement par
intersection de demi-droites avec des volumes mathématiques, et permet
des calculs allégés. Par exemple, l'intersection d'une droite
avec une sphère est plus facile qu'avec un ensemble de polygones
approchant la forme de la sphère.
ü De façon plus étendue, la
géométrie de construction de solides accélère tous
les calculs de projection : clipping, culling, ombres... Il est en effet
plus rapide de projeter un polygone formé par les arêtes d'un
solide que de projeter les polygones du solide.
ü Les calculs de collision entre deux solides convexes
sont très rapides, il suffit de tester si au moins un des deux à
un point inclus dans l'autre.
ü Le calcul d'éventuelles réflexions ou
réfractions à l'intérieur des volumes est facilité
car on connaît précisément les équations
décrivant la surface du volume, en particulier la normale et la
tangente.
b. Inconvénients
ü La liberté de modélisation est restreinte
par les possibilités de créer le volume désiré par
un ensemble d'opérations. De plus les formes présentes dans le
monde réel sont peu ou pas géométriques et même un
ballon n'est pas parfaitement sphérique lorsqu'il est posé sur le
sol.
ü On peut facilement arriver à des
hiérarchies d'opérations très complexes qui vont alourdir
les calculs de rendu.
ü Le nombre de primitives disponibles va directement
influer sur l'algorithme de rendu car ce dernier doit savoir les prendre toutes
en compte ce qui peut alourdir son écriture.
I.3.5. Modélisation
Volumique
Quand on parle de la modélisation volumique, on fait
allusion au voxel (mot-valise, créé par analogie
du mot pixel, en y contractant « volume »
et « element »).
Quand on parle de voxel, on sous-entend un pixel en 3D. Il
consiste à stocker une information colorimétrique avec ses
coordonnées spatiales, voire temporelles, de positionnement ainsi que,
facultativement, une taille relative à l'unité utilisée ou
d'autres informations telles qu'une matière. Il s'inscrit plus
généralement dans des espaces matriciels, bien que les espaces
vectoriels lui soient favorables. On notera que ses coordonnées
spatiales peuvent être polaires.
Le point faible du format (par rapport à la 3D
vectorielle) est de nécessiter énormément de ressources,
tant pour le stockage que pour le rendu qui ne bénéficie pas
d'accélération matérielle. Cependant, des algorithmes de
compression traditionnels à l'imagerie numérique ou
l'informatique peuvent être employés sans difficulté.
Le voxel est principalement utilisé
pour le rendu des terrains dans les jeux vidéo (Outcast étant un
de ses grands représentants) en utilisant une heightmap combinée
avec un Y-Buffer. La technique consiste à afficher le terrain colonne
par colonne en ne prenant en compte que les voxels dont la hauteur est
supérieure au Y-Buffer, ce dernier prenant comme valeur la hauteur de la
dernière colonne affichée. Les parties non visibles de la
scène sont ainsi tout simplement ignorées lors du rendu, ce qui
offre un fort gain de ressources.
Une des optimisations les plus remarquables offerte par le
voxel apparaît lorsque l'on passe de l'utilisation d'une matrice de voxel
à l'utilisation d'un
arbre ayant comme racine
chaque voxel et dont chaque noeud père est un voxel faisant la moyenne
de ses fils (couleur, texture). Plusieurs optimisations apparaissent
alors :
ü Premièrement, si un noeud contient plusieurs
fils ayant toutes les mêmes caractéristiques (couleur, texture),
alors il est possible de les supprimer sans perdre en détail ;
ü Deuxièmement, le niveau de détail peut
être géré très facilement en parcourant en
profondeur l'arbre et en s'arrêtant dès que la taille du voxel est
inférieure à la taille d'un pixel.
Ces deux optimisations permettent un gain de mémoire
mais surtout une vitesse d'affichage équivalent quel que soit le niveau
de détail de l'objet, son gros désavantage étant son
coût lors de la modification de l'arbre qui devient alors énorme
là où une matrice le gérerait aisément. Le dessin
par triangle reste donc le plus courant dans les moteurs 3D.
Quelques moteurs 3D utilisant un rendu par voxel :
ü WinUFO et SimUFO. Il existe un applet Java pour tester
WinUFO en ligne. SimUFO permet d'éditer directement le paysage dans le
programme ;
ü Auto-montage est un moteur hybride de 3D temps
réel de nouvelle génération destiné aux jeux
vidéo gérant la géométrie tant en voxel qu'en
vectoriel, la physique et l'éclairage.
I.3.6. Modélisation
Paramétrique
La modélisation paramétrique vous fait voir un
mode de fonctionnement des logiciels de
conceptionassistéeparordinateur
actuels. Elle n'est rien d'autre que la conception
paramétrique. Il s'agit de définir une entité par
des paramètres qui peuvent être modifiés facilement. De
cette façon, on change aisément la définition de la
pièce.
Les paramètres peuvent être de plusieurs
types : intrinsèques (longueurs, angles), cartésiens
(coordonnées par rapport à un repère), situationnels
(distance, angle entre 2 éléments)
Et quand on parle d'une contrainte, on sous-entend un
paramètre que l'on ne veut pas pouvoir modifier.
a. Fonctions
Les logiciels de CAO paramétrique se
caractérisent par la présence d'un historique. Cet historique est
généralement représenté sous la forme d'un arbre
reprenant les différentes opérations effectuées,
appelées fonctions (feature en anglais, d'où l'appellation
anglaise Parametric feature based modeler). Ces fonctions sont
généralement créées à partir
d'esquissesvariationnelles.
b. Logiciels de CAO utilisant la conception
paramétrique
ü 3Design ;
ü Autodesk Inventor ;
ü Autodesk Fusion 360 ;
ü CATIA ;
ü FreeCAD, logiciel libre multi-plateformes ;
ü OpenSCAD, logiciel libre multi-plateformes ;
ü Open CASCADE ;
ü Pro/Engineer ;
ü Revit ;
ü Solid Edge ;
ü Solidworks ;
ü Top Solid.
I.4. Quelques logiciels de
modélisation tridimensionnelle [9]
Un logiciel de modélisation 3D, ou modeleur 3D, est un
logiciel qui sert à créer des scènes 3D, composées
de formes complexes, ou objets, en trois dimensions à partir de
primitives de bases ou de définition analytique.
Les logiciels de modélisation 3D se basent
essentiellement sur la manipulation de formes de base dans un espace
tridimensionnel sur trois axes généralement notés X, Y, Z.
Ces formes de base utilisées peuvent être des cubes, des
sphères ou des cônes, mais aussi des courbes de Bézier ou
des NURBS. L'utilisateur peut en ajouter ou en enlever à
volonté.
Voici quelques logiciels de modélisation 3D le plus
utilisé :
I.4.1. SketchUp
SketchUp est un logiciel 3D à la fois puissant et
facile à apprendre. On le considère un peu comme le crayon du
dessin numérique. Ce logiciel maintes fois primé rassemble un
ensemble d'outils à la fois simples et complets qui permettent de
rationaliser et de simplifier le dessin en 3D sur votre ordinateur. SketchUp
est utilisé par tous ceux qui souhaitent rêver, concevoir et
communiquer en 3D.
Il est disponible en versions personnelles et
professionnelles. Google SketchUp (gratuit) est disponible gratuitement sur
sketchup.google.com.
Pour ceux qui veulent la version Professionnel, il est en
vente sur le site http://sketchup.google.com/gsu6/buy.html.
Une foi vous vous procurer de ce dernier, vous aurez la
facilité de :
ü Exporter des modèles dans les formats de
fichiers 3DS, DWG, DXF, OBJ, XSI, VRML et FBX ;
ü Utiliser des outils de mise en page pour créer
des pages et des présentations sur écran de vos
modèles ;
ü Bénéficier d'une assistance technique par
e-mail pendant deux ans après votre achat.
L'interface de SketchUp est ainsi plus proche d'un Illustrator
que d'un logiciel de 3D classique : on se surprend à ajouter, modifier
ou déplacer des formes à sa guise.
I.4.2. Blender
Blender est un excellent logiciel libre truffé d'outils
de pointe en termes de modélisation, de rendu, d'animation 3D et
même de montage vidéo.
a. Points forts
ü Blender est un logiciel gratuit et libre;
ü C'est aussi un logiciel performant;
ü Blender est très léger : environ 20 Mo;
ü Enfin, il est multiplateforme (Windows, Linux, Mac OS
X...).
b. Points faibles
ü Tout Blender est en anglais...
ü Le logiciel est un peu difficile d'utilisation au
début. Eh oui, Blender n'est pas en français et il est un peu
dégoutant quand on l'utilise les premières fois.
I.4.3. FreeCAD
FreeCAD est une application open source de modélisation
3D paramétrique, conçue principalement pour concevoir des objets
de la vie courante. La modélisation paramétrique décrit un
certain type de modélisation, où la forme des objets 3D que vous
concevez est contrôlée par des paramètres. Par exemple, la
forme d'une brique peut être contrôlée par trois
paramètres: hauteur, largeur et longueur.
Dans FreeCAD, comme dans d'autres modeleurs
paramétriques, ces paramètres font partie de l'objet et restent
modifiables à tout moment après la création de l'objet.
Certains objets peuvent avoir d'autres objets comme paramètres, par
exemple, vous pourriez avoir un objet qui prend notre brique comme
entrée et crée une colonne à partir de celle-ci. Vous
pouvez voir un objet paramétrique comme un petit programme qui
crée les géométries voulues à partir de
paramètres.
Voici une liste des logiciels qui sont conçus pour la
modélisation 3D :
|
Liste de logiciels de modélisation
3D
|
|
Orientation
|
Nom
|
Licence
|
|
3DReshaper
|
Propriétaire
|
|
3D Turbo
|
Propriétaire
|
|
Aartform Curvy 3D
|
Propriétaire
|
|
AC3D
(en)
|
Propriétaire
|
|
Art of Illusion
|
FLOSS
|
|
Dessin technique
|
AutoCAD
|
Propriétaire
|
|
Scène
|
Autodesk 3ds Max
|
Propriétaire
|
|
Autodesk Maya
|
Propriétaire
|
|
Autodesk Softimage
|
Propriétaire
|
|
Scène
|
Blender
|
GPL
|
|
BlockSCAD
|
|
|
CATIA
|
Propriétaire
|
|
Ceetron 3D Components
|
Propriétaire
|
|
Cheetah3D
(en)
|
Propriétaire
|
|
Cinema4D
|
Propriétaire
|
|
DAZ 3D
(en)
|
Propriétaire
|
|
Electric Image Animation System
(en)
|
Propriétaire
|
|
Flux (software)
(en)
|
|
|
Dessin technique
|
FreeCAD
|
LGPL2+
|
|
Hexagon
|
Propriétaire
|
|
Houdini
|
Propriétaire
|
|
ImplicitCAD
|
|
|
Mathématiques
|
K3DSurf
|
GPL2
|
|
Dessin technique
|
LibreCAD
|
FLOSS
|
|
LightWave 3D
|
Propriétaire
|
|
Humains
|
MakeHuman
|
FLOSS
|
|
Fractales
|
Mandelbulb3D
|
FLOSS
|
|
Fractales
|
Mandelbulber
|
FLOSS
|
|
Mathématiques
|
MathMod
|
FLOSS
|
|
MASSIVE
|
Propriétaire
|
|
MikuMikuDance
|
|
|
Mixamo
|
Propriétaire
|
|
Multigen Creator
|
Propriétaire
|
|
Modo
|
Propriétaire
|
|
OpenFX
|
|
|
OpenSCAD
|
FLOSS
|
|
Poser
|
Propriétaire
|
|
Remo 3D
(en)
|
Propriétaire
|
|
Rhinoceros 3D
|
Propriétaire
|
|
Sculptris
(en)
|
Freeware
|
|
Seamless3d
(en)
|
FLOSS
|
|
Sensable Freeform
|
Propriétaire
|
|
Shade 3D
(en)
|
Propriétaire
|
|
Silo
|
Propriétaire
|
|
Sketchup (Trimble)
|
Propriétaire
|
|
SOCET SET
(en)
|
Propriétaire
|
|
SolidWorks
|
Propriétaire
|
|
Fractales
|
Structure Synth
|
FLOSS
|
|
Swift 3D
(en)
|
Propriétaire
|
|
Tekla Structures (Trimble)
|
Propriétaire
|
|
TeoWin
|
Propriétaire
|
|
Objet
|
TopMod
|
FLOSS
|
|
TrueSpace
(en)
|
Propriétaire
|
|
Wings 3D
|
FLOSS
|
|
ZBrush
|
Propriétaire
|
|
ZW3D
|
Propriétaire
|
Tableau I.1. Logiciels de modélisation
3D
La pratique sans théorie est comparable à un
maçon qui veut construire une maison sans le plan. Connaissant 3D, nous
devons maintenant la mettre en pratique en utilisant un langage de
programmation qui y va ensemble avec le 3D. Alors, dans le chapitre suivant,
nous allons voir comment faire cette programmation avec les logiciels de
modélisation 3D.
Chap II. Programmation 3D
[5,7,9,10,12]
II.1. Introduction
Dans le chapitre précédent, nous avons
parlé de la généralité sur la modélisation
3D. Etant informaticien, la généralité sans
pratique ; ne nous ramène à rien. Voilà pourquoi nous
abordons ce chapitre dans lequel on va donner les éclaircissements sur
ce que ce la programmation 3D. Elle se défini comme étant effet
d'établir ou de réaliser un programme.
En outre, pour bien faire notre programmation, on doit bien
comprendre la nuance qu'il y a dans les différents types d'algorithme de
base pour la programmation 3D à savoir :
ü L'algorithme 2D ;
ü L'algorithme 3D.
En plus de ça, on doit connaitre quelques
bibliothèques qui permettent à ce qu'on puisse effectuer cette
programmation. Il en a plusieurs mais quand à ce chapitre, nous avons
choisi les plus utilisé et les plus fréquenté par les
développeurs en 3D. Entre autre :
ü OpenGL ;
ü DirectX ;
ü Java3D.
II.2. L'algorithme de base
deux dimensions [5]
Parlant de l'algorithme 2D, on ne traite que des moyens
d'effectuer le dessin des éléments graphiques de base sur une
grille discrète (Ecran d'ordinateur). Ces moyens en deux dimensions sont
celles qui sont utilisées pour l'affichage de tout objet graphique.
La représentation d'un objet en trois dimensions n'est
faite qu'après sa projection sur le plan 2D de l'image, et se finalise
donc par un ensemble de primitives (Dessin) en deux dimensions. Il est donc
important de disposer d'algorithmes trop efficaces. Etant dans le 2D, on a deux
axe : x et y.
Pour la modélisation 2D, nous avons trois types
d'algorithme à savoir :
ü Traçage de droite ;
ü Remplissage ;
ü Clipping.
II.2.1. Traçage de droite
[5,9]
Pour faire les traçages des droites, nous avons deux
algorithme à savoir :
ü Algorithme Simple ;
ü Algorithme de Bresenham (ou Algorithme point milieu).
a. Algorithme Simple
C'est la meilleure des algorithmes pour la
représentation de la droite (y=ax+b avec x se trouvant à
l'intervalle des points du plan).
int i,j;
double a,b;
a = (double)(j1 - j0) /
(double)(i1 - i0);
b = j0 -a*i0;
for(i=i0; i<=i1; i++) {
j = (int)( a*i + b );
putpixel(i,j);
}
b. Algorithme de Bresenham
(ou algorithme du point milieu)
L'algorithme de Bresenham est un algorithme qui permet
à ce qu'on puisse avoir une itérative de pixel suivant la
façon à minimiser l'erreur avec le segment continu, partant du
pixel pi0, j0.
On considère le cas où 0 <a<1 et
i0<i1. Alors, si pi, j est un pixel se
déplaçant sur le segment discret partant de pi0,
j0 et allant vers pi1, j1, sa position
suivante est soit pi+1, j (il avance horizontalement), soit pi+1,j+1 (il avance
en diagonale). L'algorithme suivant n'utilise des opérations que sur les
entiers, et correspond au cas où 0 <a<1.
II.2.2. Remplissage
Le remplissage d'une courbe fermée discrète
consiste à allumer les points de l'écran qui correspondent
à la partie de l'espace discret délimitée par cette
courbe. Nous présentons le cas où la courbe est un polygone
à n sommets{Pi} avec i=1...n.
L'algorithme de remplissage consiste alors à partir du
point le plus à gauche et à suivre la suite des segments qui
composent le polygone jusqu'au point le plus à droite.
Pour se faire, nous avons deux types d'algorithme de
remplissage :
ü L'algorithme de remplissage du polygone
convexe ;
ü L'algorithme de remplissage du polygone quelconque.
Figure II.1: Polygone convexe
rempli.
a. Remplissage d'un polygone
convexe
Un polygone convexe est une figure plane à plusieurs
angles.
Dans le cadre de 2D, pour la représentation de ce dernier,
on utilise l'algorithme suivant :
1. Initialisation
Pi = le plus à gauche des sommets. SH le segment
montant qui part de Pi. SB le segment descendant qui part de Pi. x = l'abscisse
de Pi.
2. Faire
(a) Mettre à jour les segments SH et SB (si on atteint
l'extrémité droite du segment, on passe au segment suivant). (b)
Calculer l'ordonnée yH du point d'abscisse x sur le segment SH. Calculer
l'ordonnée yB du point d'abscisse x sur le segment SB. (c) Tracer le
segment vertical reliant (x,yB) à (x,yH). (d) Incrémenter x de
1.
3. Tant que x n'a pas atteint l'ordonnée du point le
plus à droite du polygone.
Figure II.2: Polygone convexe.
b. Remplissage d'un polygone
quelconque
Quand le polygone n'est plus convexe, sa forme peut devenir
très complexe. Dans ce cas on ne gère plus
séparément les segments inférieurs et supérieurs
mais on détermine à chaque étape la liste des
intersections de l'ordonnée courante avec le polygone (en comptant
double l'intersection avec un sommet). En partant du bord, on trace les
segments reliant les intersections paires aux intersections impaires.
Voici l'algorithme découlant correspondant :
1. Initialisation
x =l'ordonnée du point le plus à gauche.
2. faire
(a) calculer la liste des intersections avec le polygone et
trier cette liste (on note 2nx le nombre de ces intersections
et{(x,ui)}i=1..2nx la liste triée)
(b) tracer les nx segments qui relient (x,u2i) `à
(x,u2i+1) (i va de 0 ` a nx -1). (c) Incrémenter x de 1.
3. tant que x n'a pas atteint l'ordonnée du point
le plus à droite du polygone.

Figure II.3: Polygone quelconque.
II.2.3. Clipping
251654144Dans cette partie, on ne s'intéresse qu'au
problème du clipping d'un segment par un rectangle.
Figure II.4: Ensemble de droites. La zone de
clipping est déterminée par les droites en
pointillés.
Pour le résoudre, on utilise l'algorithme de
Cohen-Sutherland. Et l'algorithme renvoie la partie du segment incluse dans le
rectangle et rien si le segment n'en fait pas partie. Et voici son
algorithme :
Segment COHEN-SUTHERLAND ( rectangle [Pmin,Pmax], segment
[P1,P2])
1. déterminer les codes binaires B1 et B2 de P1 et P2
2. si B1 =0et B2 =0alors retourner P1, P2. sinon si B1&B2
=0 alors retourner rien. sinon
(a) si B1 =0alors P1 =INTERSECTION([Pmin,Pmax],[P1,P2], B1)
(b) si B2=0alors P2 =INTERSECTION([Pmin,Pmax],[P2,P1], B2)
(c) retourner COHENSUTHERLAND([Pmin,Pmax],[P1, P2])
et la fonction Intersection par :
point INTERSECTION(rectangle [Pmin,Pmax], segment [Pd,Pf],
byte B,)
1. si le 1er bit de B =1 alors P =intersection du segment
[Pd,Pf] avec x = xmin.
2. si le 2`eme bit de B =1 alors P =intersection du segment
[Pd,Pf] avec x = xmax.
3. si 3`eme bit de B =1 alors P =intersection du segment
[Pd,Pf] avec y = ymin.
4. si 4`eme bit de B =1 alors P =intersection du segment
[Pd,Pf] avec y = ymax.
5. retourner P.
Figure II.5: Résultat
Note : L'Algorithme de Cohen-Sutherland
peut se généraliser en 3D en utilisant des plans à la
place de droite. Une de ses utilisations pratiques est de simplifier
(après rejet trivial) la géométrie à
l'extérieur du cône de vision pour ne conserver dans la
chaîne de traitement que les polygones observables ou partiellement
observables. La définition des plans associés au cône de
vision sera détaillée dans le point suivant.
II.3. L'algorithme en trois
dimensions
En ce qui concerne les algorithmes trois dimensions, nous pouvons
les classifier à deux. A savoir :
ü La base des algorithmes de clipping 3D (Le clipping est
une phase préparatoire de l'affichage ou du rendu dont le but est
d'éliminer le plus grand nombre de polygones possible afin de minimiser
la quantité objet géométrique à manipuler lors des
phases d'affichage à suivre).
ü Les algorithme d'élimination des faces
cachées des polygones présents dans une scène. Le mixage
de ses algorithmes se fait avec la méthode de rendu, qui est
présenté dans le premier chapitre.
II.3.1. Clipping 3D [5,7]
Le but du clipping en pratique est de se débarrasser du
plus grand nombre de polygones possibles pour ne se concentrer que sur ceux
effectivement visibles par l'observateur, en restreignant éventuellement
ceux qui ne sont que partiellement visible.
Il s'avère que les algorithmes vus dans le cas
bidimensionnel peuvent être facilement adaptés dans le cas
tridimensionnel moyennant quelques astuces :
ü Pour le 3D, la zone Clipping n'est plus
déterminé par des droites mais plus tôt par un ensemble des
plans (5 à 6 plans).
§ Le plan z =0 séparant les objets devant ou
derrière l'observateur,
§ Quatre plans matérialisant le cône de
vision,
§ Un plan (optionnel) correspondant à la limite du
champ de vision au-delà de laquelle les objets seront
considérés comme trop loin pour pouvoir être
observé. Si L est cette distance, le plan z = L représente la
barrière.
ü Pour le 3D, l'algorithme de Cohen-Sutherland
permet de de relier un polygone et un plan. Il a aussi comme
importance de transforme la perspective des objets.
Comparaison entre Clapping 2D et
3D
|
Claping 2D
|
Clapping 3D
|
|
Divergence
|
|
Le clapping 2D est généralement utilisé pour
relier le polygone aux droites.
|
Le clapping 3D est utilisé pour relier le polygone au
plan.
|
|
Equivalence
|
|
1.Passage dans le repère de l'observateur.
2. Clipping avec le cône de vision.
3. Mise-en-perspective.
4. Projection parallèle
|
1. Passage dans le repère de l'observateur.
2. Mise-en-perspective.
3. Clipping avec la mise en perspective du cône de
vision.
4. Projection parallèle.
|
Tableau II.1. Tableau de comparaison clipping 2D et
3D
Avec cette étude comparative, tout est maintenant
facile pour appliquer l'algorithme de Cohen-Sutherland dans le
3D (Les droites vont être représenté comme des plans).
II.3.2. Elimination des faces
cachées
L'algorithme avec élimination des faces cachées,
est subdivisé en deux sous algorithme :
ü L'algorithme du peinture
ü Algorithme du tampon de profondeur (Z-buffer)
a. Algorithme du peinture
L'idée de cet algorithme consiste à utiliser la
technique d'un peintre pour représenter une scène : il peint tout
d'abord les objets de l'arrière-plan pour terminer par les objets qui
sont les plus près (au premier plan).
En pratique, on l'applique sur des objets plats (des facettes
ou des polygones dont les points sont coplanaires) afin de limiter les
problèmes pouvant survenir lors du tri. On en distingue deux :
ü L'algorithme de peinture :
Affiche une scène avec parties cachées contenant n
polygones{Pk}k=1..n. On note Iij l'intervalle du plan de projection
correspondant au pixel (i,j), etI(i,j) l'intensité de l'image à
ce pixel. Voici l'algorithme :
image PEINTRE(entier n, liste de polygones{Pk}k=1..n)
1. Trier les polygones{Pk}de l'arrière vers l'avant.
2. Initialiser l'image de résultat I à la
couleur du fond.
3. Pour k allant de 1 à n
(a) Calculer la projection P' du polygone Pk dans
le plan de l'image. (b) Pour tous les intervalles Iij intersectant
P', Affecter à I(i,j) l'intensité de la partie du
polygone P se projetant en Iij nP'. 4. Renvoyer I
Note : On remarque que si
l'intensité de la partie polygone IijnP' est calculée
grâce à un rendu, alors ce rendu sera fait en chaque point de
l'objet, sans savoir s'ils sont effectivement visibles ou non. Une solution
consiste à dessiner les polygones en commençant par les plus
proches et à ne peindre que les pixels qui n'ont pas déjà
été peints. C'est à partir de l'algorithme à
peinture inverse que nous aurons la réponse favorable.
ü L'algorithme à peinture inverse :
la différence avec l'algorithme à peinture, c'est juste
au niveau de l'algorithme et de l'affichage. Voici son algorithme :
image PEINTREINVERSE(entier n, liste de polygones{Pk}k=1..n)
1. Trier les polygones{Pk}de l'avant vers l'arrière.
2. Initialiser l'image de résultat I à la
couleur du fond.
3. Initialiser le masque M des pixels déjà
peints à faux : M(i,j)=faux pour tout i,j. 4. Pour k allant de 1
à n
(a) Calculer la projection P' du polygone Pk dans
le plan de l'image.
(b) Pour tous les intervalles Iij intersectant P' et tel que
M(i,j)=faux,
i. Affecter ` a I(i,j) l'intensité de la partie du
polygone P se projetant en Iij nP'.
ii. M(i,j)=vrai.
5. Renvoyer I
Cet algorithme utilise le tri pour classer les objets fait
à ce qu'il ne soit pas plus rapide.
b. Algorithme du tampon de profondeur
(Z-buffer)
Cet algorithme permet d'afficher une scène avec parties
cachées contenant n polygones{Pk}k=1..n. On note Iij le carré de
la grille dans le plan de projection correspondant au pixel (i,j), etI(i,j)
l'intensité de l'image à ce pixel.
Voici comment il se présente :
image ZBUFFER(entier n, liste de polygones{Pk}k=1..n)
1. Initialiser l'image de résultat I à la
couleur du fond.
2. Initialiser l'image de profondeur Zb à +8:
Zb(i,j)=+8 pour tout i,j.
3. Pour k allant de 1 à n
(a) Calculer la projection P du polygone Pk dans le plan de
l'image.
(b) Pour tous les intervalles Iij intersectant P',
i. Calculer la profondeur z de Iij nP'.
ii. Si z<Z b (i,j) alors
affecter à I(i,j) l'intensité de la partie du
polygone P se projetant en Iij nP.
Zb (i,j)=z.
4. renvoyer I.
II.4. Quelques
Bibliothèques de programmation et modélisation 3D
Comme on l'a dit à l'introduction, sur cette partie,
nous allons parler de trois outils en faisant la présentation de ses
diverses caractéristiques, leurs implémentations et si possible
donner quelques exemples de leurs utilisations.
II.4.1. DirectX
a.
Caractéristiques
Le DirectX est nommé Game SDK. Par définition,
DirectX est un ensemble de composants développés par Microsoft
pour fournir aux applications Windows (jeux, applications multimédia,
...) un accès temps-réel et haute-performance au matériel
disponible sur le système où elles sont exécutées.
Il se place entre l'application et le matériel (carte
graphique, carte son, etc...) formant une « surcouche » de Windows,
évitant théoriquement aux programmeurs de devoir s'occuper des
différences matérielles qui existent entre les différents
PCs.
De nombreuses versions ont été
développées jusqu'à ce jour puisque nous sommes
actuellement à la version 12 et que Microsoft travaille toujours sur la
prochaine version, DirectX 13, qui sera normalement intégrée au
prochain OS.
DirectX est la propriété de Microsoft qui
possède tous les droits. Le produit n'étant pas libre, les
sources ne sont pas rendues publiques, contrairement à OpenGL.
Malgré cela, il devient un outil incontournable dans le domaine du
développement de jeux vidéo sous Windows, Microsoft passant des
accords technologiques avec les constructeurs de cartes 3D grand public.
b. Implémentation
DirectX peut être implémenté en C, C++,
C#, et Visual Basic, et ne peut évidemment n'être
développé que sous Windows. La technologie DirectX fournit un
ensemble de fonctions qui forment une interface entre le matériel et le
logiciel.
Deux couches ont été définies,
HAL (Hardware Abstraction Layer) fournit l'interface de plus
bas niveau avec le matériel (accélérateur graphique) en
masquant la spécificité de chaque carte graphique sous une
APIstandard et HEL (Hardware Emulation Layer) permet à
ce qu'une fonction de base ne serait pas "câblée".
Les Fonctions Utilisant DirectX
DirectX se décompose en fonctions gérant chacune
un aspect de la liaison entre le logiciel et le matériel:
ü DirectDraw : qui assure l'affichage de formes
géométriques à l'écran par la carte vidéo.
Il tient aussi le rôle de moteur 2D primaire.
ü DirectSound : permet la manipulation
d'échantillons sonores numérisés à partir de
n'importe quelle carte son.
ü DirectSound3D : qui permet d'ajouter une dimension
spatiale au son.
ü DirectMusic : synthétiseur logiciel pouvant
tirer parti de la présence de puces dédiées à la
synthèse sonore. Ce service permet d'obtenir une restitution de
très haute qualité notamment à travers Internet.
ü DirectPlay : qui permet de gérer une partie
des aspects réseaux que l'on retrouve de plus en plus fréquemment
dans les jeux. Le module travaille comme une couche supplémentaire
au-dessus des protocoles réseaux formels.
ü DirectInput : qui interface les
périphériques d'entrée manipulés par l'utilisateur
(claviers, souris, joysticks, joypads, etc... ). Il permet également la
gestion des controleurs à retour de force.
ü DirectSetup : qui fournit l'installation
automatisée des pilotes de DirectX et la vérification de la
version installée.
ü Direct3D : qui est le moteur de rendu 3D à
proprement parler fournissant des services élémentaires afin de
faciliter le travail aux applications dans la création de scènes
3D. Direct3D fournit des transformations géométriques (rotations,
perspectives, projections, clipping 3D, etc... ) basées sur des
opérations matricielles (4x4). Le système maintient plusieurs
systèmes de coordonnées : le port d'affichage, la vue 2D et le
monde 3D, permettant à l'application de passer aisément de l'un
à l'autre.
c. Exemple
DirectX n'est utilisé que pour le développement
de jeux vidéo même si de nombreuses applications comme les outils
de CAO (encore et toujours!) commencent à présenter une
implémentation de DirectX en plus d'OpenGL. Une des plus grosses boites
de développement utilisant grandement DirectX est
UbiSoft dont le dernier moteur, utilisé pour le jeu
SplinterCell, est celui d'Unreal (cité plus haut dans la section OpenGL)
mais rendu compatible DirectX12 et prenant donc en compte les dernières
implémentations de PixelShader3.0 et autres.

Figure II.6 : Exemple du produit de DirectX
[9]
II.3.2. OpenGL
a.
Caractéristiques
OpenGL (Open Graphics Library) est une spécification
qui définit une API multiplateformes pour la conception d'applications
générant des images 3D (mais également 2D).
Elle a vu le jour en 1992 pour succéder à la
bibliothèque de Silicon Graphics IRIS GL (SGI) qui était alors un
standard pour les ingénieurs, créateurs d'effets spéciaux
donc tout ce qui touche de près ou de loin à de la CAO
(Conception Assistée par Ordinateur).
L'expérience de SGI dans ce domaine a fait d'OpenGL une
interface facile d'utilisation, intuitive et surtout portable. Dans cette
équipe qui travaillait à l'origine sur une version similaire
à l'INRIA se trouvait le très célèbre Bui Tuong
Phong créateur de l'algorithme d'interpolation pour le lissage d'ombres.
Le projet Fahrenheit, initiative de Microsoft et de SGI, tenta
d'unifier les interfaces OpenGL et Direct3D. Celui-ci apporta au début
l'espoir de mettre de l'ordre dans le monde des APIs 3D, mais pour des
contraintes financières de la part de SGI, le projet dût
être abandonné. OpenGL est géré par un consortium
OpenGL Architecture Review Board (appelé également ARB) qui
détermine donc les modifications, ajouts et évolutions de la
norme OpenGL.L'ARB est composé de membres volants tels que ATI, Nvidia,
IBM, Intel, Sun, 3DLabs auquel s'ajoutent des membres participants tels que
Matrox ou encore Id-Software. Microsoft, l'un des membres fondateurs, s'est
retiré du consortium en mars 2003.
b. Implémentation
La version actuelle d'OpenGL est la version 4.5 et la
dernière mise à jour a eu lieu le 01/08/2016. OpenGL fonctionne
sur toutes les plateformes UNIX, sur les machines Windows, et MacOs, ainsi que
sous OS/2, OPENStep, AmigaOS, ou BeOS. Il fonctionne avec la majorité
des Interfaces graphiques: Win32, MacOS, Présentation Manager, ou
Xwindows et peut etre utilisé en Ada, C, C++, Fortran, Python, Perl et
Java.
OpenGL fonctionne à partir d'un ensemble de variables
d'états définissant le contexte GL, ces variables peuvent
être modifiées par les fonctions glEnable et glDisable.
Les Fonctions Utilisant DirectX
Un programme OpenGL s'articule autour des fonctions :
ü init() : appelée après l'initialisation
du contexte GL, permet d'initialiser les données du programme.
ü reshape() : appelée lors du redimensionnement du
contexte GL.
ü display() : fonction principale qui permet l'affichage.
ü cleanup() : appelée après la destruction
du contexte GL pour «nettoyer» le programme.
c. Exemple
Ici, nous donnerons quelques exemples d'applications utilisant
OpenGL. Le domaine dans lequel on retrouve le plus fréquemment cette
librairie est évidemment le domaine des jeux vidéo.
En effet, nombres d'entre eux utilisent OpenGL pour
développer leur propres moteurs 3D, à titre illustratif :
ü 3DStudioMax : Tout comme Lightwave3D,
il permet une émulation de Direct3D mais son rendu OpenGL est
préférable. Il est très utilisé par les
développeurs de jeu pour sa simplicité d'utilisation.

Figure II.7: Exemple de l'image produit par
3DStudioMax grace à OpenGL [9]
ü Le moteur de Quake :
développé par IdSoftware en 1996 utilise également OpenGL.
Il est le premier à être entièrement en 3Dimensions,
à utiliser des lumières temps réelles non simulées
comme dans Doom et peut lui-même être modifié à
volonté grâce au QuakeC, langage de programmation
interprété semblable au langage C. QEngine est aujourd'hui encore
en évolution et va proposer sa 4ème évolution sous peu.

Figure II .8: Exemple de l'image produit par
le moteur de Quake grace à OpenGL [9]
ü Etc.
II.3.2. Java3D
a.
Caractéristiques
Java3D actuellement à la version 1.5.2, est une
bibliothèque de classes destinée à créer des
scènes 3D (utilisation de formes complexes, d'éclairages, de
textures, d'animations, de sons ...) développée par
SunMicrosystem en 1998. Contrairement à OpenGL et DirectX qui ont chacun
leur implémentation, Java3D possède un support natif OpenGL,
DirectX et QuickDraw3D. Mais pourquoi développer Java3D alors qu'existe
déjà OpenGL et DirectX ? Le but est de faciliter la programmation
en disposant de fonctions de haut niveau ainsi que de permettre
l'écriture d'applets contenant des scènes 3D. Java3D est aussi
justifié par la portabilité de Java, ainsi une application ou
applet peut être lancée avec le même code compilé
dans toutes les plateformes ou Java3D existe (actuellement Solaris, SGI, HP-UX,
Linux et Windows).
b. Implémentation
Java3D est une extension du langage Java destinée
à créer des scènes 3D. Il se présente sous la forme
d'une bibliothèque de classes (packages J3D). Comme indiqué plus
haut, Java3D utilise OpenGL ou DirectX pour fonctionner, rajoutant un niveau
d'abstraction entre les bibliothèques 3D de base et le logiciel:

Figure II.9 : Abstraction entre les
bibliothèques 3D de base et le logiciel.
Java3D utilise la classe Transform3D pour gérer les
opérations de Translations, Rotations et Homotéties. Cette
opération est associée à une instance de la classe
TransformGroup, puis ajoutée à l'arbre de la scène pour
l'appliquer sur une forme. Il existe trois modèles de rendu pour Java3D
permettant d'espérer des optimisations conduisant à
l'amélioration de la vitesse d'affichage :
ü Immediate Mode: Permet d'utiliser ou
non la structure graphe de scène inhérente à l'API Java
3D. Plus flexible mais moins performant.
ü Retained mode : Tous les objets
définis dans le graphe de scène accessibles et manipulables par
programme, par sélection, ... Optimisation de la vitesse de rendu par
réalisation automatique d'optimisations par Java3D.
ü Compiled-Retained mode : Meilleures
performances de rendu par optimisation poussée, mais perte de la
flexibilité de programmation liée aux possibilités
d'accès et de modification des objets.
On notera enfin pour terminer sur Java3D qu'il existe une
methode compile() de la class BranchGroup permettant d'optimiser le sous-arbre
de ce BranchGroup.
c. Exemple
Peu d'applications industrielles sont
développées avec Java3D. On observe plutôt des applications
individuelles, du fait de la simplicité d'utilisation. Par exemple
Java3D est très utilisée pour la création d'applets des
sites scientifiques (représentations de molécules, simulations
physiques, ...).
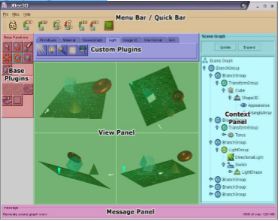
Figure II.10 : Exemple du rendu produit par
Java3D [9]
II.4. Etude comparatif des
bibliothèques
Cette étude a pour but de comparer les trois outils de
développement que nous avons choisi tout d'abord en présentant
leurs avantages et inconvénients (possibilités/limites,
facilité d'utilisation, portabilité, ...).
Avantages/Inconvénients
1. Possibilités Techniques
La première différence entre ses outils est :
Java3D se situe à un niveau supérieur à OpenGL et
Direct3D, utilisant d'ailleurs ces deux API pour son implémentation.
ü OpenGL / Direct3
Partant de l'historique OpenGL et DirectX se sont
développées en parallèle, les innovations des uns
étant rapidement suivi d'une réponse du concurrent. Aujourd'hui,
les différences de possibilités sont minimes entre les deux API;
les dernières versions (DirectX12, et OpenGL 1.5) prennent en compte
toutes les fonctionnalités classiques des moteurs 3D.
Au niveau des lumières et ombres avec calcul
automatique des normales, différents effets de brouillard,
possibilité d'utiliser des buffers spécialisés pour
gérer les effets de réflexion et de motion blur, et aussi
possibilités d'éclairage dynamique des textures par vertex ou
pixel shader.
Au niveau des textures, possibilités de textures 2D et
3D, mipmapping, transparence de textures et multi-texturing. Les deux API
permettent également l'utilisation de structures de données
facilitant l'accès aux modèles3D (vertexarray); OpenGL fournit
également des DisplayList hiérarchiques pouvant contenir la
plupart des commandes de changement d'état et de primitives graphiques
tandis que Direct3D fonctionne avec des buffers de sommets (vertex buffers)
non-hiérarchiques pour avoir un cache mémoire de
géométrie et des blocs d'états (state blocks) pour avoir
un cache de changements d'état.
Les deux normes facilitent également les optimisations,
avec l'implémentation du Zbuffer (qui cependant en DirectX n'est pas
indépendante du matériel) et l'utilisation possible de cullface.
Enfin Direct3D, contrairement à OpenGL, ne fournit pas de
mécanisme de gestion des courbes et surfaces paramétriques
(NUR
BS).
ü Java3D
La programmation avec Java3D est bien différente de
celle avec OpenGL et DirectX. En effet, ces derniers proposent une
implémentation de plus bas niveau qui permettent aux développeurs
de gérer le moindre pixel de leurs moteurs alors que Java3D
possède des fonctions de plus haut niveau, certes plus faciles
d'utilisation mais aussi plus limitées. Il est ainsi très
difficile par exemple d'implémenter des optimisations ou des effets
comme le pixel shader en Java3D.
L'avantage de ces fonctions de haut niveau est que le
développement d'applications est beaucoup plus facile. Par exemple il
existe dans les package de Java3D des fonctions permettant de détecter
si deux objets sont en collision, ce qui n'est pas le cas avec OpenGL ou
DirectX ou l'on doit tout faire « à la main », ce qui dans ce
cas est loin d'être évident.
De plus, Java3D existe dans deux versions, une OpenGL et une
DirectX, l'utilisateur peut donc choisir d'utiliser son programme avec l'un ou
l'autre des moteurs de rendu. Quand vous utilisez une version OpenGL de Java
3D, certaines fonctionnalités de l'API font appel à des
méthodes natives de la DLL Java 3D/OpenGL. Ces méthodes elles,
utilisent des fonctions de la DLL OpenGL du système qui utilise
l'accélérateur graphique disponible sur la carte graphique. Pour
terminer sur les caractéristiques techniques de Java3D, il est important
de préciser que cette librairie peut tout à fait utiliser toutes
les fonctionnalités du langage Java, ainsi il peut être
très utile d'utiliser les packages AWT ou SWING pour l'interface
graphique ou encore le package IO pour les entrées/sorties. A noter
également que Java3D utilise un package VECMATH pour le calcul vectoriel
et matriciel très utilisé dans les moteurs 3D.
2. Facilité d'utilisation
Le premier critère que nous considérerons en
terme de facilité d'utilisation est la portabilité :
ü DirectX n'est utilisable que sous Windows, et pour sa
dernière version (DirectX12) que sous les versions de Windows
supérieures à Win98.
ü Java3D quant à lui est développable sous
Solaris, SGI, HP-UX, Linux et Windows.
ü Quand à OpenGL, des implémentations
existent sur toutes les plateformes UNIX, sur les machines Windows, et MacOs,
ainsi que sous OS/2, OPENStep, AmigaOS, ou BeOS.
C'est donc OpenGL qui est la norme la plus disponible en
nombre de systèmes. DirectX12 est entièrement sous le
contrôle de Microsoft tandis que Java3D est développé par
SunMicrosystem, seul OpenGL dépend d'un consortium OpenGL Architecture
Review Board (appelé également ARB) composé par des
membres de différentes sociétés (notamment ATI, Nvidia,
IBM, Intel, Sun, 3DLabsMatrox ou Id-Software).
Si le fait d'être développé par une seule
entreprise permet d'accélérer les décisions (pas besoin de
décider d'un compromis entre différent partis), l'influence des
créateurs de cartes graphiques, ou de membres de l'industrie utilisant
OpenGL, au sein de l'ARB semble fournir une normalisation plus équitable
(la norme s'adaptant au possibilités techniques et aux besoins de
l'industrie). Le nombre de langages de programmation dans lequel une norme est
disponible influe également sur la facilité d'utilisation, le
programmeur préférant généralement
développer dans le langage qui lui est le plus familier.
DirectX comme précisé plus haut, est la
propriété de Microsoft, il n'existe donc qu'une seule
implémentation, et la norme se limite au langage C++, Visual Basic et
bien sûr C#. Java3D se présentant comme une extension de Java
n'est disponible qu'en Java.
Enfin OpenGL étant libre, de nombreuses
implémentations existent (parfois plusieurs implémentations pour
un même langage comme par exemple JOGL et JLWGL pour Java) rendant la
norme disponible en Ada, C, C++, Fortran, Python, Scheme, Perl et Java. Le
paradigme de programmation joue également beaucoup sur la
facilité d'utilisation d'une norme. OpenGL se présente comme
étant un ensemble de fonctions de bibliothèque (typiquement un
ensemble de bibliothèque à inclure et de fichier à lier
avec le programme), DirectX utilise le paradigme COM (Component Object Model),
développé par Microsoft, quand à Java3D, il utilise
évidement les capacités objets de Java, et un concept de
représentation d'une scène 3D propre à Java3D.
Chacun des paradigmes a ses avantages et ses
inconvénients, l'usage de fonctions de bibliothèque ou du
paradigme objet de java nous semble plus évident à apprendre,
mais un programmeur habitué au concept COM, préfèrera sans
doute utiliser ce paradigme. Enfin, la programmation d'un moteur 3D
étant généralement entourée par d'autres
fonctionnalités (son, réseau, entrée/sortie ...) ces
différentes fonctionnalités peuvent également influencer
le choix d'un outil. DirectX fournit en plus de DirectDraw et Direct3D, de
nombreuses bibliothèques annexes gérant différents aspects
de programmation (DirectSound, DirectInput, DirectPlay ...). OpenGL ne concerne
que le graphisme. Java3D profite quant à lui de la très riche API
java.
Bien compris les notions théoriques sur la
modélisation 3D, et là, nous venons de voir comment faire la
programmation 3D avec les différentes bibliothèques, ainsi que
les divers algorithmes qu'elle utilise ; nous devons nous mettre à
niveau de connaitre comment rendre palpable cette modélisation faite en
3D.
Le chapitre suivant sur l'étude de système
d'impression 3D, va bien nous aider à comprendre comment le faire.
Chap III. Etude de
système d'impression 3D
[4,9,10,11]
III.0. Introduction
[9,10]
L'impression 3D ou fabrication additive est au goût du
jour. Aux Etats-Unis, en France comme ailleurs, elle donne lieu à de
nombreux rapports, à un engouement médiatique et à une
innovation continuelle.
Il est une nouvelle technologie du prototypage rapide et il
est facile de fabriquer une pièce ou maquette avec précision par
exemple réalisation d'une pièce de rechange dans le domaine
spatial, ou fabrication des organes dans le domaine Biomédical, ...
La fabrication additive était plus entendue dans des
revues ou médias spécialisés évoquaient ces sujets
il y a encore quatre ou cinq ans. Mais les médias
généralistes ont pris le relais depuis lors et dans le monde
entier. Ils accordent une large place à des objets facilement
accessibles et ne manquent pas d'évoquer la sortie très
fréquente d'une nouvelle machine d'impression 3D surtout si elle n'est
pas uniquement destinée aux professionnels. Car le marché des
imprimantes 3D destiné au grand public se développe à un
rythme rapide.
L'impression tridimensionnelle est aussi décrite par
différents spécialistes comme une véritable
révolution industrielle dont les enjeux vont bien au-delà de ceux
que le grand public pourrait porter.
On retrouve ces enjeux industriels majeurs de l'impression 3D
dans les stratégies des acteurs.
Ainsi, Renault, Peugeot et Dassault Aviation ont-ils
coopéré à cette fin dès les années 90 ; des
entreprises telles que Safran y accordent la plus grande attention depuis au
moins une décennie ; GE investit dans ce domaine des sommes
considérables, etc. Et nous n'en sommes qu'à la fin du
commencement. En bref, la fabrication additive concerne absolument tout le
monde, y compris les gouvernements qui s'interrogent sur les actions
stratégiques qu'il convient de définir et mettre en oeuvre, afin
de ne pas passer à côté de ce train à grande vitesse
qui va bouleverser l'économie comme la société.
L'impression 3D fait partie de la famille des machines -outil à commande
numérique (CNC).
Avec ce chapitre, nous allons parler de l'étude du
système 3D en donnant son historique, son applicabilité dans le
marché, ses différents les matériaux de technologie et
présenté ses différents modèles économiques.
III.1. Bref historique de
l'imprimante 3D [9]
L'impression 3D apparues dans les années 1980, la
fabrication additive est une méthode de fabrication assistée par
ordinateur (CAO) définie par les organismes de normalisation nationaux
ou internationaux comme étant le procédé de mise en forme
d'une pièce par ajout de matière par empilement de couches
successives, contrairement par exemple à l'usinage qui agit par
enlèvement de matière (fabrication soustractive).
C'est le 16 juillet 1984 que le 1er brevet sur l'impression 3D
(dite « fabrication additive ») est déposé. Les
dépositaires sont français : Jean-Claude André,
Olivier de Witte, et Alain le Méhaute pour le compte de
l'entreprise CILAS ALCATEL. La même année, aux Etats-Unis, le 1er
août 1984, c'est l'américain Chuck Hull qui
dépose le brevet sur la technique d'impression 3D de
stéréolithographie (SLA pour StéréoLithographie
Apparatus).
Des expérimentations médicales ont eu lieu
depuis près d'une vingtaine d'années pour tenter des
avancées en médecine régénérative,
financées essentiellement par le gouvernement fédéral
américain. L'objectif serait de reconstituer des tissus ou des organes
à partir de cellules prélevées sur un patient malade.
En 2012, à l'aide d'une imprimante tridimensionnelle
fabriquée par LayerWise (société issue de
l'université de Louvain, en Belgique, rachetée par 3D Systems en
2014), des médecins et ingénieurs des Pays-Bas « impriment
» une mâchoire inférieure artificielle
personnalisée en trois dimensions qui est ensuite
greffée à une femme de 83 ans souffrant d'une
infection chronique des os. Cette technologie fait actuellement l'objet de
recherches afin de voir s'il serait possible de l'utiliser pour faciliter la
croissance de nouveaux tissus osseux.
En 2017, Sculpteo (un service français d'impression 3D)
présente un vélo fabriquer avec la technique d'impression 3D et
en 2018, la société Kodak, nexa 3D, Airwolf et vevo et tant
d'autres société américaine ayant comme
spécialité impression 3D, ont fabriquées plusieurs
machines pour la technologie additive.
III.2. Différents
Usages de l'impression 3D
Les technologies de fabrication additive suscitent
l'engouement de diverses industries et se retrouvent dans de nombreuses
structures, privées et commerciales, aux vocations multiples :
prothèses médicales, prototypes de
produits extrêmement divers, pièces de petite
séries ou uniques pour le domaine spatial (par
exemple télescopes pour la NASA), maquettes
d'architecture, éducation, nourriture, etc.
Les différentes applications de l'impression 3D sont
nombreuses, notamment dans les secteurs de la grande consommation, du
divertissement, de la recherche et de l'industrie. Une forte demande provient
aussi du secteur des petites entreprises qui cherchent à se
développer grâce à l'impression 3D.
Vu la pertinence de ce chapitre, et vu les divers avantages
que nous apporte l'imprimante 3D, nous devons expliciter quelques avantages
qu'il nous présente par rapport à (au):
ü Le prototype rapide ;
ü L'outillage rapide ;
ü La fabrication directe ;
ü La fabrication domestique ;
ü La réparation additive.
III.2.1. Le Prototype rapide
[4]
A l'aide de l'impression 3D, on peut fabriquer d'une
manière rapide de pièces prototypes. Le prototypage rapide
regroupe un ensemble d'outils qui, agencés entre eux, permettent
d'aboutir à des projets de représentation intermédiaire de
la conception de produits : les modèles numériques (au sens
géométrie du modèle), les maquettes.
Il fournit aux designers, ingénieurs et même aux
consommateurs un moyen idéal de première production d'objets
fonctionnels. Cela leur permet ainsi de manier et de tester les produits.
Les ingénieurs peuvent s'apercevoir plus facilement des
anomalies à corriger et sont en mesure d'optimiser facilement leur
projet.
Il a trois notions essentielles qu'on doit bien maitriser. A
savoir : le temps, le coût et la complexité des formes.
ü Temps : l'objectif du prototypage
rapide est de réaliser rapidement les modèles, dans un but de
réduction des temps de développement des produits.
ü Coût : le prototypage rapide
permet de réaliser des prototypes sans qu'il soit nécessaire de
recourir à des outillages coûteux, tout en garantissant les
performances du produit final. On est donc en mesure d'explorer les
différentes variantes du produit en cours d'élaboration.
ü Complexité des formes : les
machines procédant par ajout de matière sont capables de
réaliser des formes extrêmement complexes (inclusion,
cavité...), irréalisables par des procédés tel que
l'usinage par exemple.
III.2.2. Outillage rapide
[4]
Comme le titre l'indique, avec l'impression 3D, on a la
fabrication rapide des outils.
Dans de très nombreux secteurs, l'impression 3D s'est
progressivement tournée du prototypage vers la production d'outils pour
les processus de fabrication, dans des secteurs très divers, la
construction mécanique, l'aéronautique, la défense et
l'espace, la production de verres de très haute précision,
l'entretien de voies ferrées, par exemple.
Dans d'autres cas, l'impression 3D a fait fabriquer des
matériaux organiques, toujours en fabrication additive, certaines
petites pièces ou des supports quand nous ne trouvions plus
d'approvisionnement dans des délais raisonnables.
III.2.3. Fabrication directe
[4]
L'impression 3D intervient pour la fabrication additive des
pièces fonctionnelle.
L'imprimante 3D dans la fabrication directe, nous permet aussi
d'innover dans un mode de production totalement inconnu jusqu'alors qui
consiste à produire la même pièce sur plusieurs machines
à travers le monde, rendant ainsi possible des séries très
courtes (voire une pièce unique par machine) mais en de nombreux points
et donc finalement des séries moyennes. Le design peut être
propriétaire, mais il existe aussi de très nombreuses
bibliothèques comportant des milliers, et bientôt des millions de
fichiers dont une grande partie est en open source, les modifications peuvent
être ad hoc, la production peut être éclatée. Il
s'agit donc d'une production qui peut être locale, distribuée et
cependant significative en agrégeant toutes ces composantes (i.e. les
impressions locales) dans le temps.
L'illustration la plus frappante pour le grand public
(symbolique, vertueuse=biens communs) de ce phénomène est
l'impression de prothèses de bras ou de mains, à
très faible coûts, soit à partir de quelques modèles
déjà mis au point, soit adaptées à chaque
utilisateur.
III.2.4. Fabrication domestique
[4]
L'imprimante 3D permet à la fabrication rapide des
objets de la maison. L'impression 3D domestique permet de réparer
certains objets ou bien d'en fabriquer de nouveau. De nombreuses plat formes de
partage mettent à disposition des fichiers numériques, en effet
c'est cette partie de création de fichiers numériques qui sont
les plus difficiles à mettre en place pour un particulier. Cette
évolution d'impression 3D domestique est à remettre en
perspective avec le marché global de l'impression 3D.
III.2.5. Réparation
additive
Il permet à réparer des pièces ayant des
dommages ou des usures.
III.3. Matériaux de
technologie pour l'impression 3D
Si la mise au point de la première machine de
fabrication additive remonte à une trentaine d'année, et si l'on
traite notamment de prototypage rapide en matériaux organiques depuis
près de vingt ans, d'autres matériaux sont utilisés plus
récemment et les machines d'impression 3D sont en réalité
à l'aube d'un développement très soutenu. S'il existe des
dizaines, si ce n'est des centaines de fabricants pour des technologies de
filament plastique, il y a beaucoup moins de fabricants pour des machines
utilisant des matériaux métalliques, et encore moins pour des
matériaux de type céramiques.
Des matériaux nouveaux seront développés,
plus performants pour ce type de fabrication, les machines vont multiplier les
sources d'énergie permettant des modes de fabrication plus rapide, les
post traitements vont également se développer pour accéder
à des pièces répondant à des critères de
qualité toujours plus exigeante.
A nos jours, plusieurs pays utilisent la technologie additive
(Impression 3D) pour faciliter la fabrication rapide de leurs biens. Nous
pouvons prendre le cas des États-Unis qui ont surtout misé sur
les équipements permettant la transformation des thermoplastiques
(...mais ceci évolue rapidement sous la pression des grands acteurs,
tels que la NASA ou Boeing), tandis que l'Europe, plus particulièrement
l'Allemagne s'est positionnée sur les machines destinées à
la fabrication métallique. La majeure partie des imprimantes en
matériaux métalliques est de source européenne.
III.4. RepRap [11]
Ce mot est en anglais (Réplication Rapid Prototyper)
est un projet Britannique de l'université du Bath pour la
création d'une imprimante tridimensionnelle, ce projet réelle est
maintenant développée très activement par une
communauté mondiale à la manière du logiciel libre, a
été fondé en 2005 par Adrian Bowyer.
Il permet l'impression des objets en plastique. Etant
donné qu'il fait l'impression des divers objets en plastique, le RepRap
créé aussi des kits que tout le monde peut rassembler en fonction
du temps et du matériau.
On peut en citer six ; dont la différence
intervient juste par leurs tailles :
ü Le Darwin premier modèle

Figure III.1 : Modèle Darwin
(imprimante 3D)
ü La Mendel

Figure III.2 : Mandel Impriment (imprimante
3D)
ü Modèle Huxley

Figure III.3 : Modèle Huxley
(imprimante 3D)
ü Modèle Wallace

Figure III.4 : Modèle Wallace
(imprimante 3D)
ü Rostock
Les précédentes machines dans leur conception
prennent la forme d'un Robot cartésien, mais cette Machine elle est de
forme Robot delta plus rapide et plus précise.

Figure III.5 : Rostock (imprimante
3D)
ü Hypercube

Figure III.6 : Hypercube (imprimante
3D)
Présentant une petite généralité
sur la modélisation 3D, en ayant une connaissance à la
programmation 3D et en faisant une petite étude sur l'impression
3D ; connaissant son historique, comment on l'utilise, les
différent matériaux d'usage et en faisant voir les
différent imprimante RepRap ; nous sommes maintenant en mesure de
modélisé notre prothèse 3D de la main pour des personne
ayant perdues ladite partie. Etant dit, nous allons bien comprendre en long et
en large dans le chapitre qui suit.
Chap IV. Modélisation
3d de la Prothèse
[6,9]
Le fait de faire une conception d'un modèle physique
c'est ce qu'on appelle modélisation.
Avec le 3D, notre modélisation de la prothèse
peut se faire grâce à divers logiciels de modélisation 3D.
Mais pour notre cas, nous avons choisi Blender vu sa pertinence
énumérer dans chapitre premier ainsi qu'avec sa
bibliothèque OpenGL incorporée.
En plus de ça, Blender tourne sur tous environnements
et nous aurons la facilité d'expérimenter notre prothèse
dans n'importe quel environnement.
Nous n'allons pas tous expliquer, nous allons plutôt
donner des éléments essentiels du logiciel puis montrer le
résultat obtenu.
IV.1. Comprendre l'Interface
de Blender [6]
D'une manière purement historique, l'image de Blender a
toujours souffert de son interface, que l'on aurait pu préalablement
qualifier d'étranger.
Initialement développé pour d'anciens systèmes informatique
nommés IRIX, Blender a vu l'environnement technologique évoluer
autour de lui, tout en restant un peu à la traine par rapport à
ses congénères. Suite à ces multiples changements, les
développeurs de la Blender Foundation décidèrent de
recommencer le développement de Blender à zéro, en
imaginant une nouvelle architecture et, par la même occasion, une
nouvelle interface. La version 2.49b fut donc la dernière version de
Blender fondée sur l'ancien système.
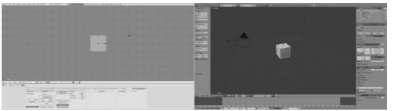
Figure IV.1 : Comparaison entre les interfaces
de Blender 2 .49b et Blender 2 .5x et suivants.
IV.2. Espace de travail
Au premier démarrage du logiciel, Blender nous
présente une interface constituée de plusieurs boutons,
répartis dans des panneaux et tournant une vue 3D.
Cette vue 3D nous propose une scène de base à
partir de laquelle nous pourrions commencer à manipuler des objets dans
l'espace.
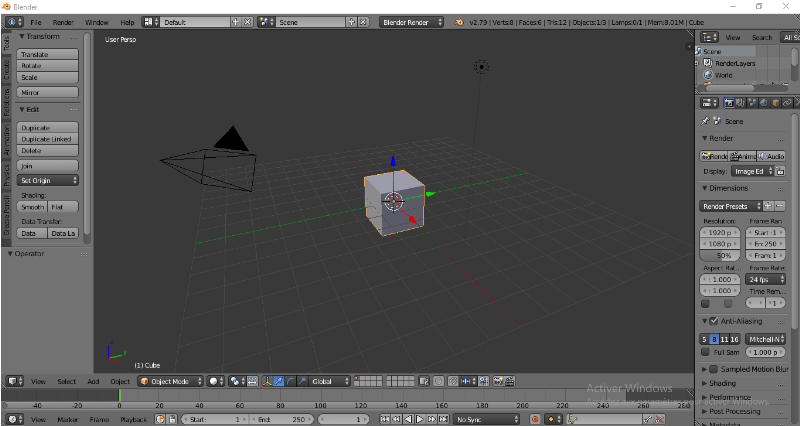
Figure IV.2 : Scène de base fournie par
Blender au démarrage du logiciel.
IV.3. Personnalisation de
l'espace de travail
Il est donc possible de segmenter l'interface de Blender en
blocs, chacun pouvant contenir un module différent. Pour assigner un
autre type de module à un bloc, par exemple pour remplacer la vue 3D
centrale par une liste des éléments présents dans la
scène, il suffit de cliquer sur l'icône se trouvant en bas ou en
haut du module en question.
En cliquant par exemple sur le petit cube gris se trouvant en
bas, à gauche de la vue 3D, nous faisons apparaitre une liste contenant
tous les modules disponibles dans Blender.
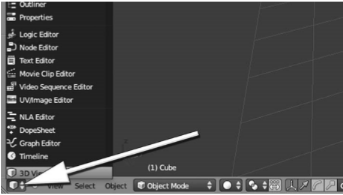
Figure IV.3 : Sélecteur des
différents modules se trouvant dans chaque bloc
IV.4. L'Interface
Utilisateur en Détail
Concernant ce point, nous allons faire le détail de
quelques interfaces les plus importants.
IV.4.1. Le Clavier et la
Souris
L'interface de Blender utilise une souris à trois
boutons et de nombreux raccourcis clavier (A voir dans d'autres manuels). Si
votre souris possède seulement deux boutons, vous pouvez émuler
le 3éme bouton dans la fenêtre de configuration des
préférences utilisateur. La molette de la souris peut être
utilisée, mais n'est pas indispensable.
Comme Blender nécessite une utilisation importante de
la souris et du clavier, « une règle d'or » s'est
répandue parmi les utilisateurs de Blender : avoir une main sur
la souris et l'autre sur le clavier. Si vous utilisez un clavier qui
est sensiblement différent de la disposition anglaise, vous pouvez
éventuellement reprendre la disposition anglaise (ou américaine)
pendant que vous travaillez avec Blender. Les touches les plus
fréquemment utilisées sont groupées de sorte qu'elles
soient accessibles avec la main gauche en position standard (index sur F) pour
un clavier anglais. Ceci suppose que vous utilisez la souris avec la main
droite.
IV.4.2. Fenêtre de
Blender
L'interface de Blender, la fenêtre rectangulaire fournie
par votre système d'opération, est divisée en plusieurs
cadres rectangulaires de fenêtre. Chaque cadre de fenêtre peut
contenir différents types d'information, en fonction du type de
fenêtre.
Chaque cadre de fenêtre opère
indépendamment des autres, et vous pouvez avoir le même type de
fenêtre dans plusieurs cadres. Par exemple, vous pouvez avoir plusieurs
Vues 3D ouvertes mais chacune présentant la Scène à partir
d'une perspective différente. Vous pouvez diviser, fusionner et
retailler les cadres des fenêtres pour les adapter à votre
travail. Vous pouvez aussi faire que quelques cadres de fenêtre
n'affichent pas d'entête pour gagner de la place.
IV. Résultat [9]
Pour la modélisation de la prothèse de main, on
fait l'assemblage juste à la fin. Donc on doit commencer à
modéliser la phalange, en suite le doigt en entièreté et
en fin de la main qui constitue notre prothèse. Mais il ne reste
qu'à signaler que l'ordre du commencement, dépend de chaque
personne.
La structure ci-dessous montre les étapes qu'on aura
besoin pour la modélisation de notre prothèse :
Figure IV.4. Etapes de modélisation de la
prothèse
IV.4.1. Modélisation de
la phalange
Pour modéliser une phalange, il faut préciser la
taille de ce dernier, préciser la longueur, la largeur ainsi que son
volume et en fin préciser l'angle qui va le séparer avec d'autres
phalanges.
Voici une représentation de la phalange du pouce et
celui de l'index. Pour les autres il suffit de faire la duplication et
préciser la taille.
 
Figure IV.5. Phalange de l'indexet du
pouce
IV.4.2. Modélisation de
la paume
Pour mieux faire les choses, on cherche à bien faire
l'angle séparateur des doigts, ainsi que la taille de la paume. Au
niveau de la paume, il faut aussi détailler la circonférence dans
la quel on va enfoncer la main. Il ne nous reste à vous signaler que le
réassemblage de tous les phalanges, doit respecter la jointure pour
créer l'articulation.
En mode édite (Ce mode permet la modification de l'objet),
voilà ce que ça donne :
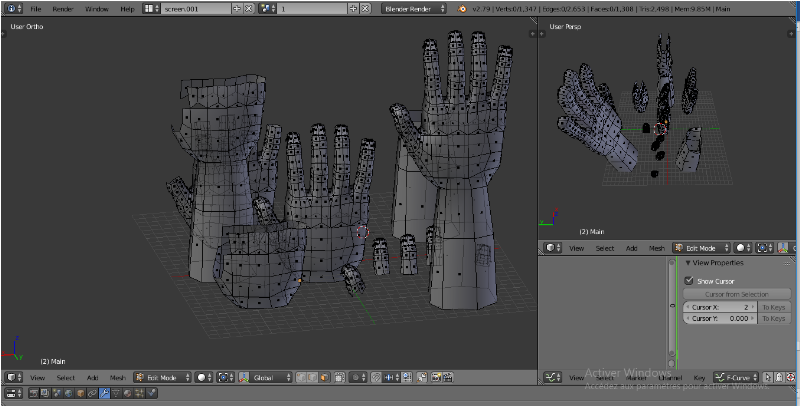
Figure IV.6. Visualisation de la prothèse en
mode Edite.
On peut aussi voir ça en Mode Objet (Le mode qui permet
de visualiser l'objet qu'on a modélisé) :
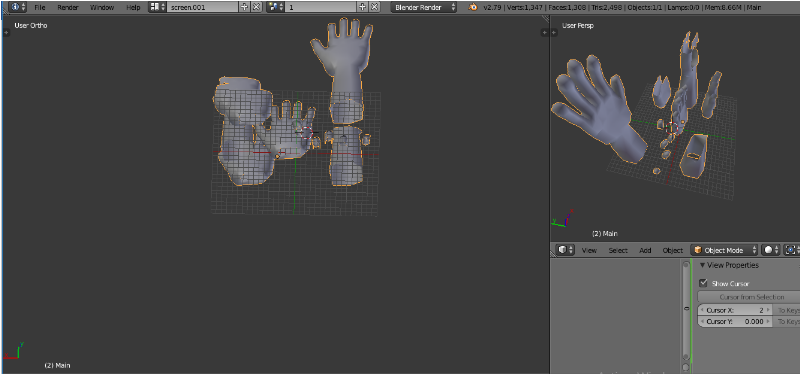
Figure IV.7. Visualisation de la prothèse en
mode Objet.
En suit, on doit voir la vue de face de la
prothèse :
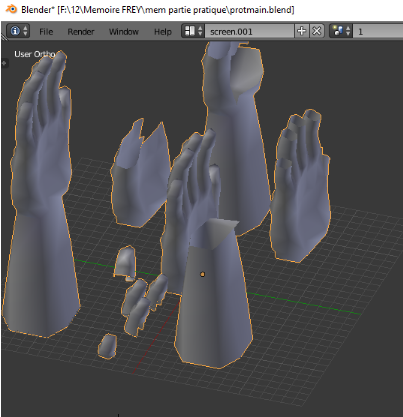
Figure IV.8. Vue de face de la prothèse en
mode Object.
Et on pourrait voir la vue Interne de la prothèse en mode
Object :
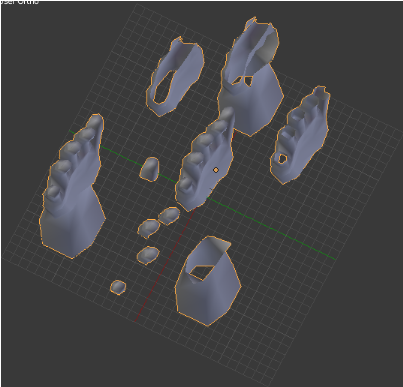
Figure IV.9. Vue Interne de la prothèse en
mode Object.
IV.4.3. La prothèse
Après réassemblage
Le réassemblage de la nôtre prothèse
consiste à mettre ensemble tous ce qu'on a pu modéliser
séparément ; Et là, on verra plus de l'importance du
moteur de rendu qu'on a pu expliciter et donner son importance dans le chapitre
premier de notre travail.
Donc on réassemble tous les doigts à la paume de
main afin de l'attacher au poignet de la main pour enfin voir notre
prothèse modéliser.
En mode Edition, voilà ce que ça nous donne
comme résultat en deux dimensions:
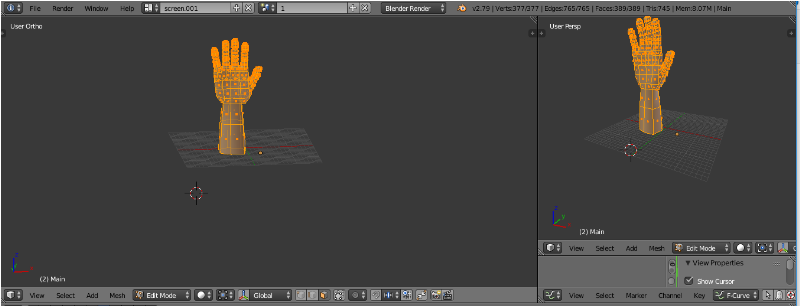
Figure IV.10. Vue finale de la prothèse en
mode Edition sous format 2D.
Et quand on quitte du mode édite au mode objet, nous avons
ce qui suit toujours en format 2D :
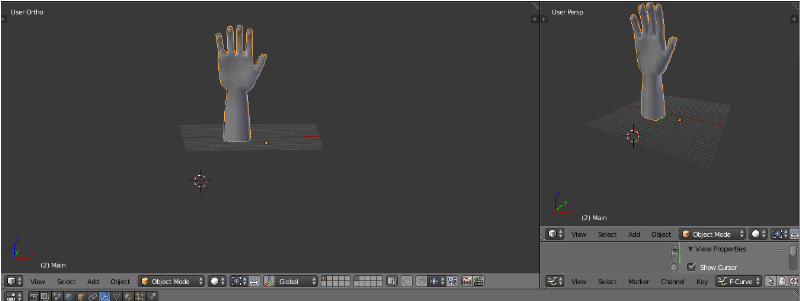
Figure IV.11. Vue finale de la prothèse en
mode Object sous format 2D.
Grace à l'affiche qui suis, qu'on pourrait voir au moins
les trois axes qui forment notre prothèse :
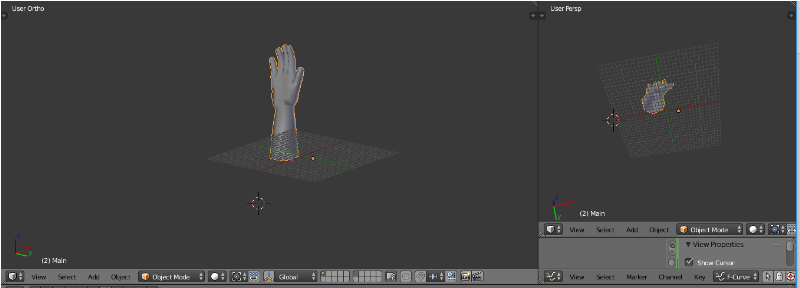
Figure IV.12. Vue finale de la prothèse en
mode Object sous format 3D.
Au final, pour voir si notre modélisation a
été bien fait, nous devons la placer sur le plateau d'impression
avec le logiciel CURA avec l'extension .stl. Si elle est entourée de la
couleur bleue, donc notre modélisation est parfaite. Et ce logiciel nous
aidera à la précision sur l'heure que ça va prendre au
moment d'impression et le montant. Pour cette version d'essai, elle coute 24$
avec 24g de filament pour l'imprimer et elle va durer 06h26min d'impression vu
qu'on a réduit la qualité et le volume.
Figure IV.13. Vue sur le plateau
d'impression.
Note :
Comme nous l'avons dit dans l'introduction de notre travail,
notre prothèse qui a été très bien
modéliser, a comme importance de permettre aux personnes vivant avec
handicap de retrouver le sourire.
Alors, il ne reste qu'à signaler : ce dernier a
des particularités qui la diffère des autres qui existent
déjà comme :
ü Notre prothèse permet à ce que les
personnes qui vont la porter, puisse faire de mouvement qui sont semblable
à la main naturelle par exemple fermer un coup de pointe. Ce qui
n'était pas le cas avec les prothèses
précédentes ;
ü Elle imite la réalité. Avec cette
prothèse, une personne qui la met, peut même oublier qu'elle a une
main artificielle ;
ü Au lieu de se déplacer pour en procurer, on va
le faire d'une manière locale et à un prix minime par rapport
à quand vous vous déplacer.
Conclusion
Nous sommes arrivés à la fin de notre
travail ; le but poursuivi a été atteint. Savons tous que le
numérique fait maintenant rage dans le monde ; et grâce
à ce dernier, on a modélisé notre prothèse 3D pour
aider nos frères vivant avec handicap à s'épanouir.
Avec cette prothèse, le porteur n'aura pas trop de
souci, car elle est similaire à la main naturelle. En plus, elle permet
à mieux faire des mouvements que les prothèses de main existant
(Comme le coup de poing).
Tous les chapitres ont servi à la réalisation et
à la finalisation de notre modèle. Souvent, il nous paraitrait un
peu drôle de voir d'autres vue en 2D. Mais grâce au moteur de rendu
vu dans le premier chapitre, qui nous a permis de visualiser notre
prothèse dans ses deux modes (2D et 3D). Il ne reste qu'à noter
que l'algorithme de Cohen-Sutherland (Clipping 2D et 3D), nous
a permis de faire le remplissage (maillage) de notre modèle.
Cette prothèse permettra aux médecins tant
spécialistes que non-spécialistes qui reçoivent les
handicapés pour ce cas, d'avoir la facilité de leur retourner le
sourire perdu pendant longtemps. Mais avant de le faire, il est toujours
conseillé de passer à des tests confirmatoires. Voilà
c'est dans cette optique que nous avons pu réaliser ce travail.
Pour arriver à la concrétisation de notre
prothèse, nous nous sommes servi de Blender qui est l'un des logiciels
de modélisation 3D avec OpenGl qui est l'une des bibliothèques
puissantes dans la modélisation 3D qui lui est incorporé.
Etant un travail humain, vos remarques et suggestions nous
seront toujours les bienvenues pour une amélioration à la
prochaine occasion.
Que Dieu bénisse tout celui qui lira ce travail.
BIBLIOGRAPHIE
Ouvrages
1. Doug Kelly, Animation et modélisation 3D :
studio pro, éd. Sybex, 2000.
2. François Goulette, Modélisation 3D
automatique : outils de géométrie différentielle,
éd. TRANSVALOR Presses des MINES, 1999.
3. Antoine Veyrat, Débutez dans la 3D avec Blender,
éd. Le Site du Zéro, Octobre 2018, 416 p.
4. Joël ROSENBER, L'Impression 3D: Porte
d'entrée dans l'industrie du 21eme siècle. (Ed 2014)
5. Pascal Mignot, Initiation à la synthèse
d'image (Mathématique dans l'infographie). Ed 2005
6. Francois Grassard, Decouverte de l'interface de Blender. Ed
2012
7. Fabrice Aubert, Introduction à la programmation 3D.
Ed.2015
8. Martin Louette, Modélisation 3D
Webographies
9. Wikipedia.org (Décembre 2018)
10.
www.fabulous.com.co/guide-impression3D/Imprimente/Domestique (decembre
2018)
11. www.reprap.org(Décembre 2018)
12.
www.google.com/amp/s/fr.softnic.com/telecharger/opengl/wins(Consultéle15/02/2019
à 3h)
Table des matières
EPIGRAPHE
i
INMEMORIAM
ii
DEDICACE
iii
REMERCIEMENTS
iv
LISTEDESABREVIATIONS
v
LISTEDESFIGURES
vi
LISTEDESTRABLEAUX
vii
INTRODUCTIONGENERALE
1
1.
PROBLEMATIQUE
1
2.
HYPOTHESE
1
3.
INTERETDUSUJET
2
4.
DELIMITATIONDUSUJET
2
5.
METHODESETTECHNIQUESUTILISEES
2
6.
SUBDIVISIONDUTRAVAIL
3
ChapI.GénéralitésurlaModélisation3D
4
I.0.Introduction[9]
4
I.1.Infographie3D[9]
4
I.2.ModèleNumériqueouModélisation3D[1,2,5,9]
4
I.2.1.Modélisation[1,5,9]
5
a.
MéthodedeModélisation
5
b.
Contraintestemporellesdanslamodélisation[5,9]
6
I.2.2.Rendu
8
I.3.Quelquestypesdemodélisation3D[8]
11
I.3.1.Modélisationàpartird'exemples
11
a.
Avantage
11
b.Inconvénients
11
I.3.2.Modélisationparcourbes(NURBS)
11
I.3.3.Modélisationparsubdivisiondesurface
12
I.3.4.Modélisationdeconstructiondesolides
12
I.3.5.ModélisationVolumique
14
I.3.6.ModélisationParamétrique
15
I.4.Quelqueslogicielsdemodélisationtridimensionnelle[9]
16
I.4.1.SketchUp
16
I.4.2.Blender
17
I.4.3.FreeCAD
17
ChapII.Programmation3D
21
II.1.Introduction
21
II.2.L'algorithmedebasedeuxdimensions[5]
21
II.1.1.Traçagededroite[5,9]
22
a.AlgorithmeSimple
22
b.AlgorithmedeBresenham(oualgorithmedupointmilieu)
22
II.1.2.Remplissage
23
a.Remplissaged'unpolygoneconvexe
23
b.Remplissaged'unpolygonequelconque
24
II.1.3.Clipping
25
II.2.L'algorithmeentroisdimensions
26
II.2.1.Clipping3D[5,7]
26
ComparaisonentreClapping2Det3D
27
II.2.2.Eliminationdesfacescachées
27
a.
Algorithmedupeinture
27
b.
Algorithmedutampondeprofondeur(Z-buffer)
29
II.3.QuelquesBibliothèquesdeprogrammationetmodélisation3D
29
II.3.1.DirectX
29
a.Caractéristiques
29
b.
Implémentation
30
c.
Exemple
31
II.3.2.OpenGL
32
a.Caractéristiques
32
b.Implémentation
33
c.Exemple
33
II.3.2.Java3D
34
a.Caractéristiques
34
b.Implémentation
35
c.Exemple
36
II.4.Etudecomparatifdesbibliothèques
36
Avantages/Inconvénients
37
ChapIII.Etudedesystèmed'impression3D
41
III.0.Introduction[9,10]
41
III.1.Brefhistoriquedel'imprimante3D[9]
42
III.2.DifférentsUsagesdel'impression3D
43
III.2.1.LePrototyperapide[4]
43
III.2.2.Outillagerapide[4]
44
III.2.3.Fabricationdirecte[4]
44
III.2.4.Fabricationdomestique[4]
45
III.2.5.Réparationadditive
45
III.3.Matériauxdetechnologiepourl'impression3D
45
III.4.RepRap[11]
46
ü
LeDarwinpremiermodèle
46
ü LaMendel
47
ü
ModèleHuxley
47
ü
ModèleWallace
47
ü Rostock
48
ü Hypercube
48
ChapIV.Modélisation3ddelaProthèse
50
IV.1.Comprendrel'InterfacedeBlender[6]
50
IV.2.Espacedetravail
51
IV.3.Personnalisationdel'espacedetravail
51
IV.4.L'InterfaceUtilisateurenDétail
52
IV.4.1.LeClavieretlaSouris
52
IV.4.2.FenêtredeBlender
52
IV.Résultat[9]
53
IV.4.1.Modélisationdelaphalange
54
IV.4.2.Modélisationdelapaume
54
IV.4.3.LaprothèseAprèsréassemblage
56
Conclusion
59
BIBLIOGRAPHIE
60

| 


