2.2.1.3. Analyse de
stationnarité des variables
Les caractéristiques stochastiques d'une série
chronologique ne peuvent être observées que si elle stationnaire
c'est-à-dire lorsque son espérance mathématique, sa
variance sont des constantes finies et que sa covariance est une fonction finie
indépendante du facteur temporel.
Pour ce faire, il est nécessaire d'étudier la
stationnarité des différentes séries à travers
l'étude des fonctions d'autocorrélation et des tests de racine
unitaire. Les fonctions d'autocorrélation permettront de
détecter une éventuelle tendance ou une saisonnalité dans
le processus stochastique. En ce qui concerne les tests de racine unitaire, ils
renseigneront sur le type de non stationnarité de la série qui
peut être de type déterministe TS ( Trend Stationnary )
ou de type aléatoire DS (Differency Stationnary ). Quelque soit
leurs natures, les séries sont stationnarisées par écart
à la tendance et par le filtre aux différences dont le nombre
permet de déterminer l'ordre d'intégration de la variable
(Bourbonnais, 2005).
Pour étudier la stationnarité des variables nous
avons utilisé le test de Dickey-Fuller Augmenté (ADF).
2.2.1.4. Le modèle
économétrique
Nous allons nous inspirer du modèle de Solow tel que
spécifié par Mankiw, Romer &Weil (1992). Dans ce
modèle, le capital humain est traité comme facteur de production
additionnel au capital physique, à la population, et à la
technologie comme dans l'équation ci-dessous :
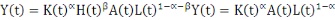 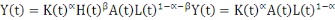 (1) (1)
Y, K, H, A et L représentant respectivement le niveau
de la production, le capital physique, le capital humain, la technologie et la
force de travail.
En dissociant le capital privé du capital public, nous
obtenons la fonction de production définie par l'équation (2)
ci-après :
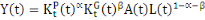 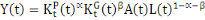 (2)
(2)
Dans cette équation nous avons fait une distinction
entre le capital privé  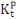 et le capital public et le capital public 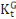 . Les fonctions d'accumulation du capital privé et du capital
public sont données par les équations 3 et 4
respectivement : . Les fonctions d'accumulation du capital privé et du capital
public sont données par les équations 3 et 4
respectivement :
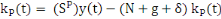 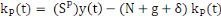 (3) (3)
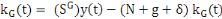 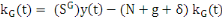 (4) (4)
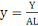  , , 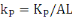  , , 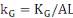 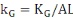 représentant respectivement la production, le capital physique
et le capital humain par unité de travail effectif. représentant respectivement la production, le capital physique
et le capital humain par unité de travail effectif.   et et   sont les taux de croissance de la population et de la technologie. Nous
avons supposé que le capital privé et le capital public se
déprécient au même taux. sont les taux de croissance de la population et de la technologie. Nous
avons supposé que le capital privé et le capital public se
déprécient au même taux. 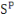 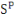 et et 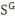 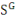 sont les parts de la production investies dans le capital privé
et dans le capital public. En combinant la fonction de production et les
équations d'accumulation, on a : sont les parts de la production investies dans le capital privé
et dans le capital public. En combinant la fonction de production et les
équations d'accumulation, on a :
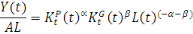

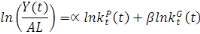
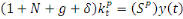
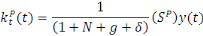
De même
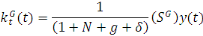
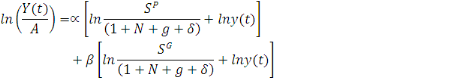
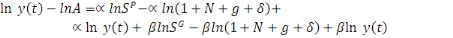


Posons  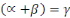 , on a : , on a :
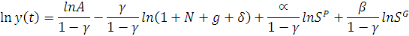
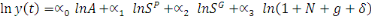
Or  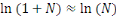
Ainsi 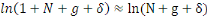 
Alors
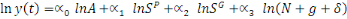
Comme nous sommes dans un modèle de Solow, A(t)
étant exogène, le capital ne se déprécie pas  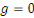 ( (  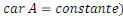 . .
De plus, on considère le fait que dans la
réalité, la population ne croît pas à un taux
constant et on obtient l'équation 5 ci-après :
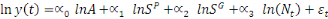  (5) (5)
L'équation 5 montre que le PIB par tête
dépend à chaque période de la technologie, de
l'investissement privé, de l'investissement public et de la croissance
démographique. L'équation à estimer peut alors se
présenter de la manière suivante:
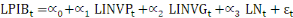  (6) (6)
Avec « L » désignant le logarithme
de la variable concerné ; PIB le Produit Intérieur Brut par
tête, 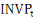 la formation brut de capital fixe du secteur privé en
pourcentage du PIB, la formation brut de capital fixe du secteur privé en
pourcentage du PIB,   la formation brut de capital fixe du secteur public en pourcentage du
PIB, et la formation brut de capital fixe du secteur public en pourcentage du
PIB, et  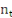 le taux de croissance de la population. le taux de croissance de la population.
En considérant que l'investissement privé et
l'investissement public dans l'équation 6 sont des variables
endogènes, on peut également définir deux équations
d'investissement.
En 2001, Kamgnia & Touna Mama ont défini une
fonction d'investissement pour le Cameroun où la variable
dépendante, l'investissement privé, dépend du PIB
réel, du crédit au secteur privé, de l'investissement
public, du taux de change, du déficit budgétaire, et de la dette
extérieure. Cette analyse ne fait cependant pas de distinction entre les
secteurs (transport, énergie, télécommunication),
et ne prend pas en compte l'impact de la maintenance. En s'inspirant de ce
travail, nous définissons deux fonctions d'investissement telle que
spécifiées dans les équations 7 et 8 ci-après :
  (7)
(7)
  (8) (8)
En effet, l'investissement Privé est influencé
par la production de l'année antérieure, le crédit
à l'économie, l'investissement public, la dette extérieure
et les recettes fiscales.
De même, l'action gouvernementale en investissement est
soumise à des pressions sociales liées à la demande en
énergie et en eau ; ici respectivement matérialisée
par la consommation en énergie de la SBEE et la vente d'eau de la SONEB.
CRED représente le crédit au secteur
privé en pourcentage du PIB, TAXE représente le pourcentage des
recettes fiscales dans le PIB. DET représente la dette extérieure
en pourcentage du revenu national, CONS désigne la consommation en
énergie ou en eau. Sur la base des équations 6, 7 et 8, nous
définissons un système :
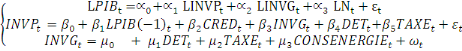
(9)
| 


