2.3. Modélisation économétrique
En utilisant les données annuelles des pays de l'UEMOA
(hors Guinée Biseau), la présente étude vise à
évaluer l'impact de la fluctuation des cours de pétrole sur
l'inflation et le solde budgétaire global hors dons sur la
période 1981 à 2015 surdes séries temporelles. Elle
recherche à déterminer le lien de cause à effet entre les
chocs pétroliers et ces deux critères clés de convergence
dans un contexte de politique monétaire commune et de budgétaire
souveraine. Il s'agit donc d'apprécierl'impactde ces variables aux chocs
pétroliers et laconduite de la politique budgétaire et
monétaire enréponse à ces chocs. La plupart des
études empiriques antérieures ont utilisé la
modélisation VAR pour estimer les impacts de la variation des cours de
pétrole sur les différentes variables macroéconomiques. La
présente étude utilise également cette technique
d'investigation au regard de la pertinence de la méthode dans le cadre
d'analyse des effets de chocs. Il est procédé àla
spécification du modèle utilisé, aux tests de racine
unitaireà l'ordre d'intégration,autest de spécification du
modèle d'estimation, et aux tests de validation du modèle.
2.3.1. Spécification du
modèle : Modélisation VAR
Le Vecteur Autorégressif(VAR) est un modèle
statistique développé par Christopher Sims au début des
années 1980 qui permet de capturer les interdépendances entre
plusieurs séries temporelles. La principale caractéristique de la
modélisation VAR est qu'elle considère toutes les variables du
système comme endogènes et fait régresser chaque variable
courante dans le modèle pour toutes les variables dans le modèle
retardé pour un certain nombre de périodes. Ainsi cette
techniquedispose d'un modèle structurel moins restrictif.
Soit le modèle VAR(p) utilisé par KENKOUO
(2014)dont la forme réduite générale est formulée
comme dans l'encadré qui suit :
Encadré :Forme réduite du
modèle VAR(p)
Xt =  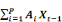 + áDt + Et avec t = 1,
..., T (1) + áDt + Et avec t = 1,
..., T (1)
Avec Xt un vecteur de dimension (6 × 1)
contenant les variables du logarithme népérien de l'inflation
(LN_INF), du prix du baril de pétrole (LN_PP) et de la masse
monétaire (LN_MM) etdu le solde budgétaire global hors
dons(SBGHD), transferts et subventions (TR_SUB) et droits et Taxes (D_T) tous
les trois rapportés au PIB nominal ;
Ai est une matrice (6 × 6) des coefficients
sur les valeurs retardées de Xt ; Dt est un
vecteur des variables déterministes (constante et tendance);
Et représente les erreurs qui sont
supposées indépendamment et identiquement distribuées
selon une loi gaussienne de paramètres (0,Ó).
Par la transformation algébrique de Fuller, la forme
VECM du modèle VAR (p) de la relation (1) se réécrit comme
suit :
?? Xt = ??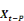  + + 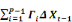  + áDt + Et avec t = 1,
..., T (2) + áDt + Et avec t = 1,
..., T (2)
0ù Ð = 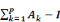  et et 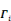  = = 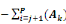 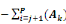 j = 1, ..., P-1 j = 1, ..., P-1
L'hypothèse de cointégration est formulée
sur le rang de la matrice Ï de la relation (2) correspondant au nombre de
relations de cointégration. Toute matrice carrée d'ordre n, de
rang réduit r pouvant toujours se décomposer en produit de deux
matrices de plein rang colonne de formats (n, r) et (r, n), nous pouvons poser
Ï = çâ' ; avec une matrice (n, r) (avec r < n) contenant
les vitesses d'ajustement pour chaque vecteur de cointégration et
â une matrice (r, n) contenant les r relations de cointégration.
Ces deux matrices sont de rangs complets. Avec ces hypothèses, la
relation (2) devient :
?? Xt = çâ'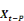  + + 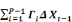 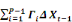 + áDt + Et avec t = 1,
..., T (3) + áDt + Et avec t = 1,
..., T (3)
Dans l'estimation du modèle de la relation (3), le test
de cointégration de Johansen utilisé dans cette étudeest
fondé sur les valeurs propres de la matrice Ï suivant l'approche de
la forme réduite. Le test de Co-intégration est
conditionné sur la non stationnarité des séries. En effet,
les tests de racines unitaires permettent de déterminer l'ordre
d'intégration des différentes séries et la
nécessité de la spécification du modèle.
Les logiciels économétriques permettent de
vérifier les tests de cointégration et la spécification du
modèle à utiliser. Lorsque les séries sont
intégrées de même ordre, il y a suspicion de
cointégration, et l'étape suivante est le test de
cointégration.Dans ces conditions, trois situations sont
possibles :
Ü Pour r = n : il n'existe pas de relation de
cointégration. Il est à estimer un modèle VAR à
niveau sur les Xt). Il y a possibilité d'analyse des réponses
impulsionnelles.
Ü Pour r = 0, il n'y a pas de relation de
cointégration et le modèle requis à estimer est une
modélisation VAR en différence sur les ÄXt.
Ü Pour 0 < r < n : il existe r relations de
cointégration. Le modèle d'estimation approprié est le
modèle à correction d'erreur VECM.Il y a possibilité
d'analyse des réponses impulsionnelles.
| 


