3.1.3 L'estimation du
Modèle Vectoriel à Correction d'Erreur
Le modèle Vectoriel à Correction d'Erreur (MVCE)
intègre une dynamique de court terme autour d'une relation de long terme
aussi appelée "relation de cointégration". L'estimation du MVCE
requière comme préalable la spécification du nombre de
relation de cointégration (ou relation de long terme) et du nombre de
retard optimal dans la dynamique de court terme.
La spécification du modelé ci-dessus a fait
l'objet d'une modification. En effet, l'introduction de la variable taux de
change rend invalide le modèle dû au fait que le coefficient du
résidu retardé n'est pas compris entre -1 et 0. Cette aberration
vient du fait que TE et IPC sont corrélés à 99% comme le
montre la matrice de la corrélation entre les variables. Donc la part du
TE est prise en compte par IPC d'où la suppression du TE dans le
modèle.
Tableau 5 : Matrice de
Corrélation
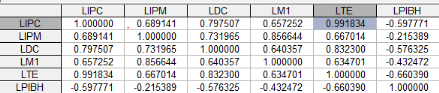
Source : Nos calculs sur
Eviews
Il ressort qu'à long terme (voir
annexe 9):
LIPC = -2.23LDC + 2.45LIPM -1.96LM1 -5.55LPIBH +
104.3
Tableau 6 : Synthèse
des résultats du modèle MVCE
|
D(LIPC)
|
D(LDC)
|
D(LIPM)
|
D(LM1)
|
D(LPIBH)
|
|
CointEq1
|
-0.099743
|
-0.425695
|
0.127363
|
-0.023428
|
-0.062920
|
|
[-2.34632]
|
[-3.27401]
|
[ 1.01398]
|
[-0.25880]
|
[-2.00039]
|
|
|
D(LIPC(-1))
|
0.189934
|
-0.054032
|
-0.105549
|
-0.206158
|
0.043652
|
|
[1.17161]
|
[-0.10897]
|
[-0.22035]
|
[-0.59718]
|
[0.36392]
|
|
|
D(LDC(-1))
|
0.026352
|
-0.258752
|
-0.318064
|
0.011180
|
-0.010475
|
|
[ 0.39740]
|
[-1.27576]
|
[-1.62332]
|
[0.07918]
|
[-0.21349]
|
|
|
D(LIPM(-1))
|
-0.244291
|
-0.350285
|
0.215769
|
0.027770
|
0.019302
|
|
[-2.70368]
|
[-1.26749]
|
[0.80820]
|
[0.14433]
|
[0.28871]
|
|
|
D(LM1(-1))
|
0.146767
|
0.274739
|
0.220336
|
0.305691
|
0.174605
|
|
[1.28255]
|
[0.78495]
|
[0.65165]
|
[1.25445]
|
[2.06215]
|
|
|
D(LPIBH(-1))
|
0.725014
|
2.028454
|
-0.001171
|
-0.083695
|
0.354408
|
|
[1.90553]
|
[1.74305]
|
[-0.00104]
|
[-0.10330]
|
[1.25889]
|
|
|
C
|
0.031273
|
0.069294
|
0.045425
|
0.037150
|
-0.017809
|
|
[2.03980]
|
[1.47772]
|
[1.00275]
|
[1.13791]
|
[-1.56989]
|
Source : Nos calculs sur Eviews
sur les données de la BM
Ce tableau montre qu'à court terme:
D(LIPC) = 0,031 + 0.189D[LIPC(-1)] + 0,026D[LDC(-1)] -
0,24D[LIPM(-1)] + 0,47D[LPIBH(-1)] + 0,146D[LM1(-1)] -
0,099RESIDU(-1)
RESIDO1 (-1) est le résidu retardé d'une
période. Son coefficient (-0,09) qui représente la force de
rappel vers l'équilibre est significatif, négatif et compris
entre -1 et 0. Le modèle vectoriel à correction d'erreur est
valable.
v Test de causalité de Granger
Théoriquement, la mise en évidence de relations
causales entre les variables fournit des éléments de
réflexion à une meilleure compréhension des
phénomènes économiques. Une variable Y est dite
causée au sens de Granger par une autre variable X, si X aide dans la
prédiction de Y, de même si les coefficients des variables
retardées de X sont statistiquement significatifs. A notre niveau, le
test est basé sur l'idée selon laquelle les variables causent
globalement l'inflation sous les hypothèses:
H0 : les variables ne causent pas
l'inflation
H1 : les variables causent
l'inflation
La probabilité associée au test est de 0,088 et
inférieure à 10%; ce qui amène à rejeter
l'hypothèse nulle selon laquelle, globalement les variables ne causent
pas l'inflation au seuil de 10%.
| 


