Efficacité de la politique monétaire sur la stabilité de taux de change en République démocratique du Congo de 1998 à 2014.

2. Tests économétriques

Ces tests se fondent sur les tests des résidus et sur leurs stabilités.

§ Tests sur les résidus

Examiner les résidus est un des moyens les plus s rs d'évaluer la qualité de la régression, Pour cela, nous allons nous intéresser aux tests suivants :

· Test de normalité de résidus de JARQUE-BERA

Le principe de ce test repose sur le calcul des coefficients d'asymétrie A et d'aplatissement K. Cette statistique est calculée par la formule :

Où A est le coefficient d'asymétrie, calculé à partir du moment d'ordre 3 (Skewness) :

K est le coefficient d'aplatissement de PEARSON calculé à partir du moment d'ordre 4 (Kurtosis) :

Cette statistique suit une loi de Khi-carré avec 2 degrés de liberté. Le test se formule en posant :

H₀ : il y a normalité des résidus ;

H₁ : pas de normalité des résidus,

Règle de décision : Si la valeur de JB calculée est supérieure à la valeur du Khi-carré de la table (5,99 à 5%), on rejette alors l'hypothèse nulle et par conséquent la distribution des résidus n'est pas normale.

Avec l'application sur Eviews, la statistique de Jarque-Bera doit être inférieure à 5,99 ou soit sa probabilité doit être supérieure à 0,05, pour valider l'hypothèse nulle, Sinon, on valide l'hypothèse alternative.

· Test de Multiplicateur de LAGRANGE :

Ce test examine la corrélation entre les résidus et la probabilité des valeurs retardées à un degré supérieur, Le critère de validation repose sur les hypothèses ci-après :

H₀ : il y a absence d'auto corrélation des erreurs

H₁ : il y a présomption d'auto corrélation des erreurs

La probabilité de NR² doit être supérieure à 0,05 pour que H₀ soit validée, au cas contraire, on valide l'hypothèse alternative.

§ Test d'auto corrélation des erreurs de Durbin-Watson

Ce test permet de vérifier s'il y a l'auto corrélation d'ordre 1 des erreurs.

Pour l'application pratique de ce test, on calcule la statistique de Durbin-Watson (d) de la manière suivante : ; d varie toujours entre 0 et 4. 0 = d = 4.

Il repose sur les hypothèses suivantes :

H₀ : il y a absence d'auto corrélation d'ordre 1

H₁ : il y a présomption d'auto corrélation d'ordre 1

On lit dans la table de Durbin-Watson, au seuil de 5% et Durbin-Watson doit être à l'intervalle de 1.5 à 2.4, il doit être proche de 2 pour validerH₀ dans le cas contraire on valide H_1.

§ Test de l'hétéroscedasticité

Pour vérifier l'hétéroscedasticité, nous faisons recours au test de WHITE et ou de celui d'ARCH. Ces deux tests posent les mêmes hypothèses et le même critère de validation :

H₀ : il y a homoscédasticité ;

H₁ : il y a hétéroscedasticité,

On accepte H₀ si la probabilité de NR² est supérieure à 0,05, L'inverse est valable pour accepter H_1.

§ Test de colinéarité (test de Klein)

Ce test permet de voir s'il y a multicolinéarité entre les variables exogènes ou pas. Il y a multicolinéarité entre les variables dans un modèle de régression lorsqu'il existe une relation linéaire parfaite ou presque parfaite entre quelques ou toutes les variables explicatives.

Elle résulte dans un modèle où les variables exogènes sont liées. La liaison entre les variables exogènes peut être relative. C'est le cas qu'on rencontre fréquemment. Elle peut être absolue ; c'est le cas qu'on rencontre si le modèle a été mal spécifié.

On évalue R²

Si r²xj>R² : on admet qu'il y a colinéarité entre xi et xj ;

Si r²<R² : on admet qu'il n'y a pas colinéarité.

§ Test de stabilité du modèle

Ces tests permettent de voir au seuil d'erreur de 5%, si le modèle est stable à travers le temps.

Pour effectuer ce test on peut passer par :

· Test de Chow

Ce test se calcule de la manière suivante :

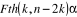
Ho : SCR = SCR₁ + SCR₂, le modèle est stable ;

H1 : SCR ? SCR₁ + SCR₂, le modèle est instable.

Si Fcal>Fth, on rejette Ho.

Lorsque les données ne sont pas suffisamment élevées par sous échantillon, on utilise le test de Chow réduit. Il s'agit du test sur un seul sous échantillon : le sous échantillon ayant plus ou moins 15 données.

On construit dans ce cas la statistique F du test comme suit :

Où n₁ = taille de l'échantillon total

n₂ = taille du sous échantillon

Cette statistique suit une distribution F de Fisher à n₂ et (n₁ - k) degrés de liberté. Si F_C> F_T, on rejette Ho.

Avec l'application sur le logiciel Eviews, les coefficients du modèle sont stables si probability est supérieur à 5%.

Les coefficients du modèle sont instables si probability est inferieure ou égale à 5%.

On choisi les dates de rupture

· Test de CUSUM (Brown, Durbin, Ewans)

Pour cusum on fait un modèle de cadrage. Les résidus vont se présenter dans un cadrant.

Ho : si la courbe ne coupe pas le corridor : modèle est stable

H1 : si la courbe coupe le corridor : le modèle est instable.

ü Test de CUSUM

Ce test permet de détecter les instabilités structurelles.

ü Test de CUSUM Carré

Ce test permet de détecter les instabilités ponctuelles.

Si la courbe ne coupe pas le corridor : modèle est stable

Si la courbe coupe le corridor : le modèle est instable.

Le corridor est en pointillés

§ Test de spécification du modèle (test de Ramsey)

Le test de Ramsey consiste à vérifier si la forme fonctionnelle est correcte.

Nous vérifions cela en utilisant les hypothèses suivantes :

Ho : P>0,05 : le modèle est bien spécifié ;

H1 : P<0,05 : le modèle est mal spécifié.