4.4 Détection et localisation de
défauts
4.4.1 Détection de défauts
Une fois que le modèle KPCA a bien
étéidentifié, on peut passer à l'étape de
détection et localisation de défauts. Deux défauts ont
étésimulées sur les variables X3, X18 du nouveau set de
données, entre les instants [450, 550] et [650, 750] respectivement,
avec une amplitude qui s'élève à environ 25% de la plage
de variation de ces variables.
KPCA Indice SPE cas sain
4
2
8
6
0
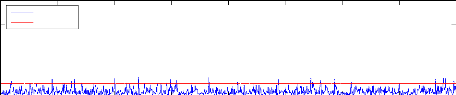
SPE
Seuil à 95%
100 200 300 400 500 600 700 800

KPCA - Indice SPE cas défaillant
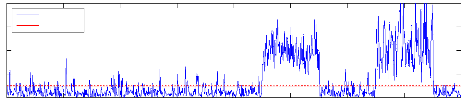
4
2
8
6
0
SPE
Seuil à 95%
100 200 300 400 500 600 700 800
38
Figure 4.5 - Évolution de l'ndice SPE cas sain et
défaillant
Détection et localisation de défauts
Application
39
4.4.2 Localisation de défauts
Une fois le défaut est bien détectépar
l'indice de détection, une étape d'isolation de ce défaut
intervient pour savoir la provenance de cette défaillance. On utilisera
la méthode du Kernel PCA partielle pour l'isolation des défauts.
Elle permet une structuration des résidus par construction d'un ensemble
de modèles, de tel sorte que chaque modèle est sensible à
certaines variables et insensible à d'autres. Les modèles sont
construits d'après la matrice d'incidence suivante (Table des signatures
théoriques).
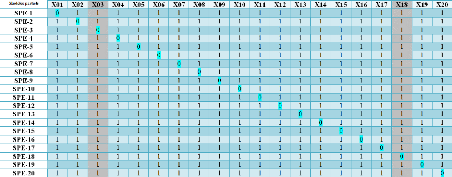
Figure 4.6 - Table des signatures théoriques
Dans cette approche on a construit 20 modèles du KPCA.
Chaque modèle est insensible à une (01) variable comme il est
bien illustrésur la table des signatures théoriques qui montre la
structuration des modèles choisis. La (Fig 4.7) montre
l'évolution de la signature expérimentale lorsqu'un défaut
intervient sur les variables (capteur/actionneur)
du système. La signature expérimentale est
obtenue après codification des résidus. Oùun
dépassement est codépar 1 et un non dépassement est
codépar 0. Ce qui permet d'obtenir les deux signatures théoriques
:
La premiére : ( 1 1 0 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 ). Cette signature est identique à la
3emme colonne de la table des signatures
théoriques. Cela veut dire que la variable (capteur/Actionneur)
affectépar le premier défaut est X3.
La deuxième : ( 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 0 1 1 ). Cette signature est identique à la
18emme colonne de la table des signatures
théoriques. Cela veut dire que la variable (capteur/Actionneur)
affectée par le deuxième défaut est X18.
Détection et localisation de défauts
Application
40
KPCA Indice SPE pour les dix premiers modèles
réduits
5
0

SPE 1
100 200 300 400 500 600 700 800
5
0

SPE 2
0 100 200 300 400 500 600 700 800
5
0

SPE 3
0 100 200 300 400 500 600 700 800
5
0

SPE 4
100 200 300 400 500 600 700 800
5
0

SPE 5
100 200 300 400 500 600 700 800
5
0

SPE 6
100 200 300 400 500 600 700 800
5
0

SPE 7
0 100 200 300 400 500 600 700 800
5
0

SPE 8
0 100 200 300 400 500 600 700 800
5
0

SPE 9
100 200 300 400 500 600 700 800
5
0

SPE 10
100 200 300 400 500 600 700 800
Détection et localisation de défauts
Application
KPCA - Indice SPE pour les dix derniers modèles
réduits

5
0
SPE-11
0 100 200 300 400 500 600 700 800

5
0
SPE-12
0 100 200 300 400 500 600 700 800

5
0
SPE-13
0 100 200 300 400 500 600 700 800

5
0
SPE-14
0 100 200 300 400 500 600 700 800
5
0

SPE-15
0 100 200 300 400 500 600 700 800

5
0
SPE-16
0 100 200 300 400 500 600 700 800

5
0
SPE-17
0 100 200 300 400 500 600 700 800
5
0

SPE-18
0 100 200 300 400 500 600 700 800

5
0
SPE-19
0 100 200 300 400 500 600 700 800
5
0

SPE-20
0 100 200 300 400 500 600 700 800
41
Figure 4.7 - L'évolution des SPE des modèles
réduits
42
| 


