Etude de la convection naturelle turbulente dans une enceinte a paroi chauffee

I.2 La convection naturelle en cavité differentiellement chauffée.

I.2.1 Les bases de la convection naturelle en cavité

L'étude de la convection naturelle dans les enceintes a fait l'objet d'un très grand nombre de travaux tant théoriques qu'expérimentaux. L'intérêt de telles études réside dans son implication dans de nombreuses applications industrielles telles que le refroidissement des composants électroniques, la thermique des bâtiments, l'industrie métallurgique, la croissance des cristaux pour l'industrie des semi conducteurs, et le cas d'une génération de chaleur accidentelle due à un incendie dans un bâtiment pour réacteur nucléaire, etc.... L'enceinte rectangulaire continue à être la géométrie qui présente le plus d'intérêt.

I.2.1.1 La cellule de Rayleigh-Bénard

C'est Henri Bénard à la fin du XIX^e siècle fut l'un des premiers à mener une étude en laboratoire sur les courants de convection. Dans son article intitulé Les tourbillons cellulaires dans une nappe de liquide, (Bénard H., 1901), étudie des couches minces de fluides (environ 1 mm) chauffées en-dessous, la surface supérieure du liquide étant libre. La cellule de Rayleigh-Bénard est plus proche de celle définie théoriquement par Lord Rayleigh en 1916.

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 13

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

En effet, contrairement au dispositif expérimental de H. Bénard, il fait l'hypothèse dans son article que le fluide est contenu entre deux plaques planes infiniment grandes. Lors du calcul du seuil d'instabilité du fluide, c'est-à-dire la différence de température pour laquelle le fluide se met en mouvement, l'auteur introduit également une quantité qui deviendra par la suite le nombre de Rayleigh (Rayleigh L., 1916). Rayleigh place lui même son travail dans la continuité de celui de H. Bénard qu'il cite dès la première phrase de son article. En réalité, nous savons maintenant que la théorie développée par Rayleigh ne s'applique pas à l'expérience de H. Bénard.

En 1900, H. Bénard commente son travail en ces termes : « Je n'est pas la prétention d'avoir épuisé un sujet aussi nouveau : bien des points restent à éclaircir, même sans sortir du point de vue expérimental ; mais je serais heureux si mon travail, tout incomplet qu'il est, contribuait à attirer l'attention des expérimentateurs sur les domaines inexplorés de la Physique moléculaire et de la Mécanique des fluides. ». Il semble que son souhait ait été réalisé : la cellule de Rayleigh-Bénard reste encore aujourd'hui un dispositif d'étude de la convection thermique très utilisé. Il s'agit en effet d'une géométrie simple avec peu de paramètres de contrôles qui peuvent être ajustés indépendamment les uns des autres. Cependant, malgré le grand nombre d'études sur ce sujet, des zones d'ombre persistent, en particulier la compréhension du mécanisme de transport de la chaleur par l'écoulement turbulent à haut nombre de Rayleigh.

I.2.1.2 Problème posé par la convection naturelle

Le problème de la convection naturelle dans les cavités différentiellement chauffées a été posé par Batchelor en 1954 (Djanna F., 2011), il fut le premier à définir les régimes de conduction

et de couches limites. Il a examiné en détail les cas de faibles nombres de Rayleigh (Ra < ) et a
fait une analyse qualitative pour des valeurs plus élevées du nombre de Rayleigh. Il ressort de son étude que, lorsque l'on soumet les parois verticales d'une cavité remplie d'air à un écart de température constant, les paramètres principaux donc dépend l'écoulement engendré sont :

? Le nombre de Rayleigh :

? le nombre de Prandtl:

? le rapport de forme vertical :

Les nombreuses publications de (Busse F., 1967) témoignent de l'intérêt qu'il a porté à l'étude des instabilités de Rayleigh-Bénard. Il a en effet établi un diagramme qui donne les différentes instabilités en fonction de trois paramètres, à savoir: le nombre d'onde, le nombre de Prandtl et le nombre de Rayleigh.

Le cheminement principal du fluide dans une cavité différentiellement chauffée avec parois en vis-à-vis est donné ci-dessous : une fois l'écart de température imposé, le fluide monte au niveau

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 14

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

de la paroi chaude, rejoint la paroi froide en longeant le plafond (jet pariétal), puis, redescend au niveau de la paroi froide, enfin, rejoint la paroi chaude par le plancher. De plus, suivant les conditions limites imposées, il se peut que des zones de recirculation apparaissent. On peut également observer suivant les cas de figure, le développement des couches limites le long des parois chaude et froide, ainsi que la transition vers la turbulence ou même la turbulence pleinement développée (R_a grand).

Figure 8 : Représentation schématique de l'écoulement pour un nombre de Rayleigh égal à
1,5×10⁹ (Salat J., 2004)

Une question centrale est notamment de savoir comment évolue l'efficacité du transfert thermique avec l'augmentation du nombre de Rayleigh. Le nombre de Rayleigh (Ra) est un paramètre de contrôle du système. Il peut être vu comme la différence de température sans dimension, c'est-à-dire que plus il est élevé, plus l'échange de chaleur est important (Gautier F., 2008). Nous verrons que peu importe le régime, le Rayleigh est le moteur de la modification de la stratification thermique de l'écoulement, et qu'a une valeur dite Rayleigh critique (transition entre le régime laminaire et le régime turbulent), il change complètement l'allure de l'écoulement.

I.2.2 Paramètres influençant l'écoulement de convection naturel en cavité

I.2.2.1 Influence du nombre de Rayleigh

Le nombre de Rayleigh (Ra) est le paramètre de contrôle de la convection thermique. Plus le nombre de Rayleigh est grand, plus la convection est intense. Il s'écrit sous la forme :

Où g est l'accélération de la pesanteur, f.? le coefficient de dilatation thermique isobare, h la hauteur de la cellule de convection, ?T la différence de température entre le haut et le bas de la cellule, á la diffusivité thermique et y la viscosité cinématique du fluide. Le nombre de Rayleigh

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 15

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

peut s'interpréter comme une mesure de l'importance du mécanisme responsable de l'instabilité du fluide (la poussée d'Archimède) par rapport aux mécanismes de freinage (la diffusivité thermique et la viscosité). Il est également possible de voir le nombre de Rayleigh comme la différence de température ?T adimensionnée (Djanna F., 2011).

En général, les écoulements de convection se présente sous forme de rouleaux contra-rotatifs bidimensionnels d'axes parallèles qui apparaissent au seuil d'instabilité correspondant à une valeur du nombre de Rayleigh critique (Rac) de l'ordre de 1708. Au-dessous de cette valeur critique, on a un régime conductif. En augmentant la valeur du nombre de Rayleigh au-delà de la criticalité, des modifications dans la structure de l'écoulement apparaissent. Dans ce sens, (Krisnamurti R., 1970) a effectué des études sur le Rayleigh, et a constaté différentes transitions vers le régime turbulent en fonction du nombre de Prandtl. Il a montré que pour un fluide donné, en augmentant le nombre de Rayleigh, l'écoulement, depuis l'état stationnaire, passe par différents régimes; à savoir le régime périodique, quasi-périodique et turbulent. Néanmoins, pour les faibles valeurs du nombre de Prandtl (cas de l'air), la transition d'un état stationnaire à la turbulence s'opère directement et elle se fait pour une faible valeur du nombre de Rayleigh (Ra = 4,8 x 10³). Dans le même ordre, (Revnic C. et al., 2009), fait des expériences pour deux valeurs du nombre de Rayleigh (10² et 10³) et fait le constat qu'effectivement, plus il augmente le nombre de Rayleigh, plus les lignes des isothermes se déforment et tendent à être parallèle au plafond, en tendant vers la turbulence. Il en va de même pour le champ dynamique, qui tourne autour du centre de la cavité et s'en rapproche en fonction de l'augmentation du nombre de Rayleigh.

Lorsque le nombre de Rayleigh augmente, l'écoulement horizontal à proximité du plafond (resp. planché) est refroidi (resp. réchauffé) le long de son parcours, et lorsque le gradient local excède celui que le fluide peut supporter, ce dernier éjecte une perturbation thermique qui peut alors être absorbée par la couche limite. Cette perturbation va ensuite être amortie ou amplifiée par la couche limite verticale suivant un processus de filtrage tel que décrit par (Gebhart B., 1973). Cette perturbation est généralement amortie sur la première moitié de la couche limite avant d'être amplifiée sur la deuxième moitié. Ces perturbations thermiques ont un effet plus déstabilisant sur l'écoulement que les perturbations d'origine hydrodynamique rencontrées pour des cavités à parois adiabatiques. En effet, pour une cavité carrée remplie d'air par exemple, le nombre de Rayleigh critique pour lequel apparaissent les premières instationnarités est de l'ordre de 2×10⁸ (Le Quéré P., 1987), (Mergui S., 1993) dans le cas adiabatique alors qu'il passe à 2×10⁶ dans le cas conducteur (Le Quéré P., 1987). On peut le voir sur la figure ci-dessous qui présente la valeur du nombre de Rayleigh critique pour des cavités de rapport de forme compris entre 1 et 10. Les valeurs du nombre

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 16

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

de Rayleigh critique ont été confirmées numériquement par (Winters K., 1987), (Jones D. et Briggs D., 1989).

Figure 9 : Comparaison des courbes correspondant à la transition à l'instationnarité pour des
parois addiabatiques (---) ou conductrices (-) en cavité remplie d'air A= (H/l) (Le Quéré P., 1987)

(Ampofo F. et Karayiannis T., 2003) Ressortent les profils de température au coeur de la cavité pour un nombre de Rayleigh de 1,5 x 10⁹, et a les mêmes profils.

L'étude de la convection naturelle en régime instationnaire obéit aux Hypothèses simplificatrices suivantes (Aklouche S. et al., 2005) :

? le fluide doit être newtonien ;

? L'écoulement doit être laminaire et bidimensionnelle ;

? les propriétés physiques du fluide doivent être constantes hormis la masse volumique qui obéit à l'approximation de Boussinesq ;

? Les échanges radiatifs entre les parois, la dissipation visqueuse et le terme de pression dans l'équation de la chaleur doivent également être négligeables.

Les calculs d'Aklouche S. et al. (2005) ont été effectués pour trois valeurs du nombre de Rayleigh thermique (10³, 10⁴, 10⁵) et un nombre de Prandtl de l'air pris égal à 0,71. Les résultats sont présentés sous la forme de lignes de courant, d'isothermes et de portrait de phase. Pour les nombres de Rayleigh égaux à 10³ et 10⁵, l'écoulement est caractérisé respectivement par quatre et trois cellules. Les quatre cellules sont assimilables à des tourbillons symétriques 2 à 2 par rapport au plan médian aux parois horizontales figure 10a.

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 17

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

Figure 10 : représentation des lignes de courant. (Aklouche S. et al., 2005)

Les deux cellules localisées dans la partie inférieure gauche de l'enceinte et celles situées dans la partie supérieure droite tournent dans le sens trigonométrique tandis que les deux autres cellules tournent dans le sens horaire. La répartition des isothermes présente, comme les lignes de courant, une symétrie par rapport au plan médian aux parois horizontales. L'écoulement caractérisé par trois cellules résulte de la fusion des deux cellules situées à gauche de la diagonale de l'enceinte et la cellule du milieu tourne dans le sens trigonométrique (fig.10b et 10c).

Figure 11 : représentation des isothermes. (Aklouche S. et al., 2005)

Par contre, au milieu de l'enceinte, la forme des isothermes varie au cours du temps. Il y a un resserrement d'autant plus prononcé que le nombre de Rayleigh est élevé, des isothermes, caractérisant la prédominance du transfert de chaleur par conduction (fig.11b et 11.c).

On remarque que l'écoulement en régime chaotique apparaît pour un nombre de Rayleigh égal à 7,5 10⁵ et se manifeste jusqu'à un nombre de Rayleigh égal à 3,10 ⁶. Les différents portraits de phase caractérisant l'état stationnaire (point limite), l'état périodique (cycle limite), l'état quasi périodique (dédoublement de période), (tore) et l'état chaotique (chaos) montrent la mise en évidence de la multiplicité des solutions lorsque le nombre de Rayleigh augmente. Des fenêtres laminaires apparaissent pour un nombre de Rayleigh égal à 3,7 10⁶ dont le portrait de phase est caractérisé par un tore. Le dimensionnement des portraits de phase a révélé l'existence d'attracteurs étranges.

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 18

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

Ces résultats sont confirmés à une couche de différence lors des campagnes de mesure de vitesse, par PIV-2D effectué par (Benkhelifa A. et al., 2007), dans le plan vertical médian à mi-profondeur d'une cavité, L'examen de son champ moyen, montre que l'écoulement est caractérisé par un arrangement sous forme de trois rouleaux contrarotatifs. Qui persiste même à des écarts de température de l'ordre de 40°C pour un même nombre de Rayleigh. On observe également deux petits tourbillons de coin respectivement au niveau du coin en haut à gauche et en bas à droite. Il est intéressant de constater que cette structure organisée fait apparaître trois rouleaux, alors que l'on aurait pu s'attendre à trouver une structure à quatre rouleaux comme présenté précédemment.

Reprenons toujours un cas d'instationnarités en ajoutant dans la cavité un linteau mais pour une valeur du nombre de Rayleigh de 1,5.10⁹ (Rouger N. et al., 2007). On observe immédiatement que la circulation d'air se caractérise essentiellement par des écoulements qui suivent les parois, sans aucun décollement appréciable. En descendant le long de la paroi froide, il fait apparaître un développement de couche limite qui s'épaissit dans la partie basse. La partie inférieure de la cavité devient le siège de l'épanouissement d'un jet pariétal horizontal accompagné au-dessus, d'une recirculation bien visible à travers les vecteurs. Le long de la paroi verticale chaude, la couche limite montante se développe même au-delà de Y = 0,7 (coté inférieure du linteau), sans que l'on puisse distinguer un échappement horizontal important à cette même cote, comme cela est observé dans les cas tests de simulations numériques à plus haut nombre de Rayleigh.

Il n'y a donc apparemment pas de zone morte dans la partie supérieure gauche de la cavité, l'écoulement principal longe les parois et contourne sans décollement le linteau qui, normalement, n'est qu'un obstacle passif (adiabatique). Le linteau introduit des différences de température entre l'amont et l'aval car l'alimentation de l'espace semi-confiné en aval du linteau se fait principalement par de l'air à une température adimensionnée de l'ordre de 0,15 et qu'il n'y a plus aucun apport de chaleur en aval du linteau. Nous remarquons que le Linteau en fait ne modifie vraiment pas l'allure de la stratification thermique de l'écoulement. Elle est juste un obstacle passif pour l'écoulement qui reste influencé par le nombre de Rayleigh.

On augmente cette fois ci d'une puissance (Rayleigh de 5,85x10¹⁰ (Lasfer K. et al., 2007) en introduisant une inclinaison ô de la cavité sur l'intervalle comprises entre 70 et 110°. La figure 12 illustre la distribution des lignes de courant, des isothermes et des iso-lignes de l'énergie cinétique turbulente imposée par le nombre de Rayleigh obtenu. Nous remarquons que l'écoulement présente un aspect parallèle et une stratification thermique prononcée au coeur de la cavité et que la majeure partie de l'écoulement se déplace au niveau des parois latérales. Ceci se traduit par la formation d'une couche limite aux proximités de ces parois. On peut distinguer aussi que les lignes de courant

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 19

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

deviennent de plus en plus distordues dans la partie supérieure ou la partie inferieure de la cavité, respectivement si on augmente ou on diminue l'inclinaison à partir de 90°. Cette structure est accompagnée par des zones de recirculation dans le coin inférieur droit et le coin supérieur gauche de la cavité.

Figure 12 : a) lignes de courants, b) Isothermes, c) Iso lignes de l'énergie cinétique turbulente.
(Lasfer K. et al., 2007)

Le modèle de turbulence utilisé est le k-w de Peng-Davidson-Holmberg. Cette investigation

a permis de mettre en évidence les effets de l'inclinaison sur l'intensité de l'écoulement dans la cavité et sur le transfert de chaleur à travers les parois latérales. Le profil reste le même que dans une cavité rectangulaire avec le même nombre de Rayleigh sans inclinaison.

De Saury D. et al. (2008) on avance encore d'un cran avec le nombre de Rayleigh (1,2.10¹¹) sans inclinaisons et sans obstacle dans la cavité, et on obtient les mêmes résultats. Intéressons nous plutôt aux profils de vitesse dans la direction normale et à proximité des parois chaude, Z = 0,7 (z = 2,69 m) et froide, Z = 0,3 (AT = 20 °C) qu'ils présentent. On peut noter une faible intensité du mouvement (le maximum de vitesse ne dépasse pas 25 cm/s). Par contre, la couche limite montante est particulièrement épaisse car elle atteint 145 mm à la cote Z = 0,7.

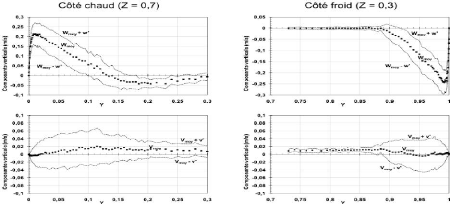
Figure 13 : Profil des composantes verticale et horizontale de vitesse dans les couches limites
montante et descendante, à la position z = 2,69 m pour un écoulement de convection naturelle. (Ra
= 1,2.10¹¹ ; å = 0,1 ; AT = 20 K). (Saury D. et al., 2008)

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 20

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

Pour montrer que le paramètre principal qui gouverne la convection thermique naturelle est le nombre de Rayleigh, qui représente le rapport des forces de flottabilité (Poussée d'Archimède) aux forces visqueuses, et est proportionnel au gradient de température appliqué, Boutra A. et al (2011) sortent l'évolution de la cartographie des isothermes pour différentes valeurs du nombre de Rayleigh. Pour les faibles valeurs du nombre de Rayleigh, il montre que la structure des isothermes reste parallèle à la paroi verticale de la cavité ce qui signifie que le transfert thermique est purement conductif dans cette zone. Remarquons que pour Ra = 10⁶, les isothermes sont plus incurvées, indiquant ainsi des gradients de température plus importants.

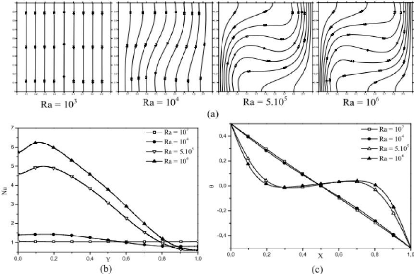
Figure 14 : Effets du nombre de Rayleigh en régime stationnaire sur: (a) les isothermes, (b) le nombre de Nusselt local relevé sur la paroi chaude, (c) le profil de température relevée sur le plan médian horizontale. (Pr = 7, Bn = 5 et Ä = 5.10⁴). (Boutra A. et al., 2011)

La figure 14 (b) représente l'évolution du nombre de Nusselt local le long de la paroi chaude (paroi verticale de gauche) pour différents nombres de Rayleigh. Nous remarquons que l'augmentation du nombre de Rayleigh augmente le nombre de Nusselt local. Les profils des températures relevées sur le plan médian horizontal (Y = 0,5) pour les différents nombres de Rayleigh sont donnés sur la figure 14(c). Pour Ra = 10³, le profil de température est linéaire étant donné que le transfert thermique est purement conductif. Pour des valeurs élevées du nombre de Rayleigh, les profils de températures se caractérisent par une épaisseur de couche limite thermique (sur les deux faces verticales) qui diminue avec l'augmentation de ce dernier.

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 21

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

On peut donc conclure en disant que, le nombre de Rayleigh permet de voir la stratification thermique de l'écoulement de convection naturelle (Pour les faibles valeurs du nombre de Rayleigh, la structure des isothermes reste parallèle à la paroi verticale de la cavité et pour des Rayleigh élevé, elle est oblique et forme des tourbillons dans l'enceinte). Et aussi que la présence d'un élément dans la cavité, ou l'inclinaison de celle-ci n'influe vraiment pas sur la stratification à un nombre de Rayleigh donnée. Nous allons maintenant voir si la variation du rapport de forme (rapport entre les dimensions de la cavité) influence sur cette stratification.

I.2.2.2 Influence du rapport de forme

Dans le cas de parois horizontales adiabatiques, Le Quéré (1987) identifie deux classes d'écoulement selon le rapport de forme vertical de la cavité :

? Pour Av = 4, l'instationnarité résulte de l'instabilité intrinsèque des couches limites verticales sous forme d'ondes progressives se propageant dans le sens de l'écoulement. La période associée à ces instabilités évolue au voisinage de Rac comme Ra-1/2 ;

? Pour Av < 4, l'instationnarité est due à la déstabilisation d'une zone à forte divergence dans les coins en sortie de couche limite d'après Paolucci et Chenoweth en 1989. La période relative à ces instabilités évolue au voisinage de Rac comme Ra^-1/2.

Si les conditions aux limites influent notablement sur l'apparition des instabilités, elles agissent également sur la structure de l'écoulement. La figure 15 (a)-(d), représentent les lignes de courant correspondant au cas d'écoulement d'air dans une cavité de rapport de forme égal à 2 ((a) et (b)) pour Ra = 2×10⁶. On peut constater la présence de mouvements de recirculation dans la partie haute et basse de la cavité dans le cas conducteur (b), inexistants dans le cas adiabatique (a). En revanche, on observe nettement la présence d'un ressaut hydraulique en aval des couches limites verticales dans le cas adiabatique (c) à Ra = 1,7×10⁸ tandis que pour le cas conducteur (d) à Ra = 1×10⁶, l'écoulement est formé par deux zones de couches limites prolongées par des écoulements horizontaux le long du plafond et du plancher. On ne note plus ici la présence de la zone décollée observée pour le cas adiabatique (c). Enfin on constate que pour cette gamme de Rayleigh, la centro-symétrie de l'écoulement est conservée aussi bien pour le cas de parois horizontales adiabatiques que pour le cas de parois conductrices.

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 22

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

Figure 15 : Comparaison de l'allure des fonctions de courant. (a) et (b) : AH= 2, Ra = 2×10⁶ (Le Quéré P., 1987) ; (c) et (d) AH= 1, RaH = 1,7×10⁸ (c) ; Ra = 1×10⁶ (d) (Henkes W., 1990)

Prenons les travaux de (Benkhélifa A. et Pénot F., 2005) effectués avec un rapport de forme vertical Av (Av = H/L) de 4. Afin de repérer les premières instationnarités pour une inclinaison è donnée (è est l'angle formé par l'horizontale et la paroi chaude de la cavité pouvant varier entre 0 et 180°), ils font varier graduellement l'écart de température entre les parois. Les mesures de température locale, associées aux visualisations par tomographie laser, lui ont permis de distinguer les différentes situations suivantes :

? Pour les faibles inclinaisons, è = 40°, le régime turbulent est atteint très tôt (dès un écart de température ?T = 1,6°C pour è = 40° et à partir de ?T = 1°C pour è = 15 et 0°). Pour è = 40°, ils ont observé un écoulement de couche limite, le long des parois actives, caractérisé par de grosses structures tourbillonnaires qui affectent le reste de la cavité. Toutefois, pour les faibles inclinaisons, l'examen attentif des visualisations fait ressortir une tendance très nette avec l'existence d'une structure cohérente organisée en trois rouleaux contrarotatifs de taille et de formes irrégulières. Pour toutes ces inclinaisons, il y a par moment, apparition de bouffées provenant de la 3^ème direction montré également par (Benkhelifa A. et al., 2007). Ces cas correspondent à des situations du type convection de Rayleigh-Bénard. On voit bien que le rapport de forme change l'instant de la stratification et non la stratification ;

? Pour è = 60°, l'écoulement passe de l'état stationnaire à deux états successifs, à savoir l'état monopériodique à un écart de température de 2°C et l'état chaotique à partir d'un écart de

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 23

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

température de 3,6°C. En effet, les visualisations effectuées à ?T = 1°C montrent principalement un écoulement de couche limite laminaire le long des parois différentiellement chauffées. Cependant, pour un écart de température de 6°C, de grosses structures tourbillonnaires circulent le long de ces parois, provoquant des mouvements secondaires très instables au coeur de la cavité ;

? Pour 60° < O = 100°, ont retrouve trois régimes d'écoulement qui se succèdent depuis l'état stationnaire ; à savoir, le régime monopériodique, le régime quasi-périodique et le régime chaotique. La différence réside uniquement dans les valeurs de l'écart de température d'apparition de ces différents modes. Par ailleurs, les visualisations effectuées pour chacun des régimes font apparaître d'abord le régime de couche limite laminaire le long des parois actives avec un coeur pratiquement au repos (mode stationnaire), puis un régime oscillatoire en haut de la couche limite chaude et en bas de la couche limite froide (mode monopériodique). En augmentant l'écart de température, ces oscillations s'amplifient avec l'apparition de temps en temps de structures tourbillonnaires ; c'est le régime quasi-périodique qui s'installe. Si l'on se situe à des écarts plus élevés, nous franchissons le seuil de l'écoulement turbulent caractérisé par des structures tourbillonnaires qui prennent naissance cette fois-ci en bas de la couche limite chaude et en haut de la couche limite froide et se développent tout le long vers l'aval. Pour ces différents régimes, ont constate des écoulements secondaires caractérisés par deux tourbillons co-rotatif et contrarotatif proches de chacun des planchers haut et bas provoqués par les décharges des couches limites sur ces parois ;

? Pour O = 120°, les analyses spectrales des fluctuations de température en haut de la couche limite chaude révèlent l'apparition successive, à des écarts de température ?T = 21,6, 26 et 31°C, de trois fréquences distinctes. Puis, deux nouvelles fréquences accompagnées d'une multiplication de pics secondaires sont perceptibles sur le spectre de puissance à partir de ?T = 33°C. En effet, si le long des parois actives un écoulement de couche limite laminaire perdure jusqu'à un écart de température égal à 33°C (où l'on observe des oscillations en haut de la couche limite chaude, et inversement en bas de la couche limite froide), le reste de la cavité semble en revanche être affecté par des bouffées 3D. Ces dernières seraient dues à la présence d'ondes de gravité et seraient à l'origine des trois premières fréquences évoquées ci-dessus, les autres fréquences sont causées par les instabilités de couche limite avec des ondes progressives de Tolmien-Schlichting.

? Pour O = 140°, un seul mode monopériodique dû aux instabilités d'ondes de gravité est observé dès un écart de température égal à 29°C et jusqu'à un écart de l'ordre de 40°C.

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 24

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

? Au-delà de 140°, aucune fréquence n'est perceptible sur les spectres, le régime conductif reste bien stable même pour les grands écarts de température (?T = 42°C).

Figure 16 : écart de température critique d'apparition des différents modes d'instationnarité
(Benkhélifa A. et Pénot F., 2005)

Pour chacun de ces résultats, On voit bien que le rapport de forme change et influence le temps d'initiation de la stratification, mais en aucun cas ne change la stratification thermique imposé par le nombre de Rayleigh. Un autre nombre adimensionnel modifie cette stratification.

I.2.2.3 Influence du nombre de Prandtl

(Boutra A. et al., 2011), montre l'influence du nombre de Prandtl sur l'évolution des isothermes dans une cavité chauffée, en sortant la cartographie des isothermes pour différentes valeurs du nombre de Prandtl. Pour les faible nombre de Prandtl (Pr » 7), ces courbes mettent en évidence un transfert convectif traduit par une forte distorsion des isothermes. En revanche, Pour les grandes valeurs du nombre de Prandtl (Pr = 10 et 20), on assiste à un comportement totalement différent du précédent, caractérisant un transfert conductif représentatif des milieux solides ou des milieux liquides pour lesquels une structure en forme de bouchon apparaitrait et occuperait la région centrale de la cavité et dont l'étendue augmenterait avec l'augmentation du nombre du Prandtl.

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 25

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

Figure 17 : Effets du nombre de Prandtl en régime stationnaire sur: (a) les isothermes; (b) le nombre de Nusselt local relevé sur la paroi chaude; (c) le profil de température relevée sur le plan médian horizontale. (Ra = 10⁵; Bn = 5 et Ä = 5 10⁴). (Boutra A. et al., 2011)

(Aounallah M. et al., 2006), La résolution numérique est basée sur la méthode de Boltzmann sur réseau. Les présents résultats montrent que les caractéristiques du transfert thermique sont fortement affectées par la variation des nombres de Rayleigh et de Prandtl.

En fait, le Prandtl en soit ne modifie pas la stratification, mais crée une forte distorsion des isothermes. Lesquels peuvent avoir une structure en forme de bouchon, et occuperait la région centrale de la cavité et dont l'étendue augmenterait avec l'augmentation du nombre du Prandtl. Le dernier paramètre et non le moindre est le couplage convection-rayonnement.

I.2.2.4 Influence du rayonnement sur la stratification thermique et le nombre de Rayleigh

La convection naturelle en cavité carrée a fait l'objet de nombreuses études numériques en tant que configuration générique représentative des applications potentielles. Mais rares sont des études qui tiennent compte du couplage de la convection naturelle avec le rayonnement même si ce couplage est inhérent en convection naturelle.

Afin d'enrichir la base de données en couplage convection naturel et rayonnement de surfaces et comprendre l'effet du rayonnement de surfaces sur la convection naturelle, un code numérique 2D a été mis en oeuvre par (Wang H. et al., 2006). Ils réalisent des études en cavité carrée remplie d'air dont les quatre parois ont la même émissivité å. En faisant intervenir

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 26

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

est la

conductivité de l'air, T est la température et qr est la densité de flux net radiatif. qr est déterminée par les systèmes d'équations.

Sur l'écoulement stationnaire, ils montrent que le rayonnement fait varier jusqu'à 10 % le nombre de Nusselt convectif. Et illustre à Ra = 10⁶ l'influence du rayonnement de surfaces sur la structure d'écoulement : les effets visibles se trouvent le long des parois horizontales et dans le coeur de la cavité.

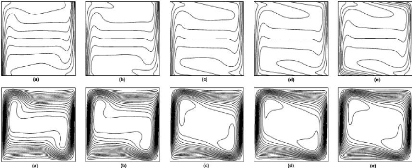
Figure 18 : influence de l'émissivité sur l'écoulement à Ra = 10⁶ avec (a) e = 0, (b) e = 0.1, (c) e = 0.4, (d) e = 0.8 et (e) e = 0 avec parois horizontales conductrices. (Wang H. et al., 2006)

Par rapport au cas sans rayonnement (E = 0), les isothermes ne sont plus normales aux parois horizontales du fait de l'échange net radiatif, la stratification diminue au centre de la cavité, les couches limites horizontales sont renforcées et enfin la paroi haute est refroidie et la paroi basse est réchauffée. Ce comportement de la température sur les paroi horizontales s'explique par le fait que la paroi haute perd de la chaleur (flux net radiatif essentiellement positif) et que la paroi basse reçoit de la chaleur (flux net radiatif essentiellement négatif). De façon qualitative, le rayonnement de surfaces a pour effet d'induire une structure d'écoulement qui ressemble plus à celle dans une cavité avec parois horizontales parfaitement conductrices (Fig. 18).

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 27

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

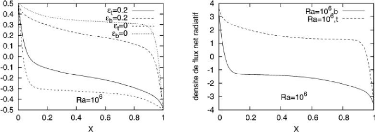
Figure 19 : température (à gauche) et densité de flux net radiatif (à droite) en parois haute

et basse à Ra = 10 ⁶. (Wang H. et al., 2006)

Pour å = 0,2, le rayonnement de surfaces modifie le transfert thermique global au moins à la hauteur de 20 % pour la gamme du nombre de Rayleigh considéré. Il est à noter que pour å fixe le nombre de Nusselt radiatif augmente non seulement avec le nombre de Rayleigh mais aussi en proportion par rapport au nombre de Nusselt convectif correspondant. Du fait que

( ) , ce qui est le cas dans ce travail à petit nombre de Rayleigh,

et que la densité de flux conductif , est utilisée pour définir Nur, le nombre de Nusselt radiatif
n'est plus qu'une fonction linéaire de H. Bien que le nombre de Nusselt convectif soit proportionnel à , il reste constant à un nombre de Rayleigh fixe. Comme Nur ~ H, pour un
nombre de Rayleigh et les émissivités fixes l'influence du rayonnement de surfaces est d'autant plus importante que H est grand sur l'écoulement instationnaire, à Ra = 1,82 X 10⁸ pour les parois horizontales adiabatiques et à Ra = 2,08 X 10⁶ pour celles parfaitement conductrices. Comme en présence du rayonnement de surfaces la structure d'écoulement ressemble plutôt à celle dans une cavité avec parois horizontales conductrices, on s'attend à un nombre de Rayleigh critique intermédiaire. Ils ont procédé de façon classique en augmentant progressivement le nombre de Rayleigh en examinant pour chaque nombre de Rayleigh étudié le comportement en temps des solutions numériques. Les premiers calculs ont été faits pour H variant de 0,265 m à 0,420 m et å = 0,2. Comme un des premiers écoulements instationnaire a été observé à Ra = 2,0 X 10⁷ avec

T = 5 K et H = 0,333 m, H. Wang et al choisissent alors de travailler avec H = 0,335 m et å = 0,2 et toute variation du nombre de Rayleigh correspond à celle de T.

Par la suite ils ont diminué progressivement le nombre de Rayleigh : 1,9 X 10⁷, 1,8 X 10⁷, 1,2 X 10⁷ et ont obtenu des solutions périodiques caractérisées par une période sans dimension de T = 5. Lorsqu'ils partent avec la solution obtenue à Ra = 1,2 X 10⁷ comme conditions initiales pour étudier Ra = 1,1 X10⁷, ils ont observé, après un long temps transitoire, une solution périodique en temps caractérisée par une période sans dimension de T = 6,5. Il s'agit d'une autre branche de solutions périodiques. En continuant de diminuer le nombre de Rayleigh, des solutions périodiques jusqu'à

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 28

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

Ra = 9,4 × 10⁶ sont obtenus. Repartant de Ra = 1,1 × 10⁷ pour des nombres de Rayleigh plus élevés des solutions périodiques avec T = 6,5 jusqu'à Ra = 1,3 × 10⁷ sont obtenu. En faisant le passage Ra = 1,3 × 10⁷ ? 1,5 × 10⁷, la solution périodique finale a une période de T = 5 est découverte. La Figure suivante résume les procédures suivies et les résultats obtenus, notamment les deux branches de solutions périodiques.

Par rapport aux études antérieures réalisées en convection naturelle pure dans une cavité carrée différentiellement chauffée avec parois horizontales adiabatiques, on conclut en premier que la présence du rayonnement de surfaces avec une émissivité des quatre parois égale à å = 0,2, fait baisser le nombre de Rayleigh critique. Comme vu ci-dessus, le rayonnement de surfaces fait tendre la structure de l'écoulement vers celle d'une cavité avec parois horizontales conductrices, il semble normal que le rayonnement de surfaces fait baisser le nombre de Rayleigh critique. Il est vraisemblable que le nombre de Rayleigh critique baissera d'avantage pour å plus grande.

(Djanna F., 2011) donne un meilleur éclaircissement en sortant la stratification thermique de l'écoulement de convection naturelle turbulente dans une cavité chauffée avec rayonnement de parois passives important. Il analyse plusieurs cas de figure :

? Stratification dans la cavité avec rayonnement de parois passives important : les parois latérales, le plancher et le plafond sont laissés bruts. Des profils verticaux de température au centre de la cavité ont été obtenus pour plusieurs écarts de température, et donc pour différents nombre de Rayleigh.

Figure 20 : Stratification thermique avec des parois d'émissivité importante pour différents AT

(Djanna F., 2011)

Cette figure donne l'évolution de la température adimensionnée O (= (T - Tm)/AT) en fonction de la hauteur adimensionnée Y (= y/H). On constate, sur cette figure que, l'écart de température ne modifie pas de façon significative l'évolution de la température au centre de la cavité. Cette évolution est d'ailleurs relativement linéaire au coeur de la cavité, et on retrouve la

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 29

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

tendance centro-symétrique de ce type d'écoulement. Cette linéarité disparaît lorsque l'on s'approche du plafond ou du plancher et l'on observe une dispersion des températures. Ceci s'explique en partie par un rayonnement de paroi non négligeable.

Afin de mieux comparer, les phénomènes qui se produisent au centre de la cavité, le paramètre de stratification thermique S a été calculé pour chaque essai. Ce paramètre traduit l'évolution du gradient vertical sans dimension de température. Il est définit par

H0T 09

s= = I-3

L'évolution de ce paramètre, en fonction de la différence de température entre les deux parois actives ou en fonction du nombre de Rayleigh, est reportée dans le tableau 1. Toutefois ce nombre reste quasiment constant égal à une valeur de 0,45 quelque soit la différence de température. L'étude de l'incertitude sur S montre que la dispersion sur ce paramètre ne dépasse pas 8 % avec peut être une tendance vers la diminution avec l'augmentation (tendance régressive due à l'augmentation) du nombre de Rayleigh.

Tableau 1 : Paramètre de stratification mesuré avec rayonnement important des parois passives.

(Djanna F., 2011)

LT(K)	10,0	15,0	17,4	20,0
Ra	5,8 x 10^10	8,6 x 10^10	1 x 10^11	1,2 x 10^11
S	0,47	0,44	0,44	0,41

? Stratification dans la cavité avec émissivité faible des parois passives : Les parois avant et arrière, le plancher et le plafond sont maintenant recouverts des feuilles d'aluminium de très faible émissivité (å = 0,10#177; 0,05) et d'épaisseur 40 um. Comme précédemment, des profils verticaux de température ont été obtenus pour plusieurs différences de température, et donc pour différents nombre de Rayleigh.

Figure 21 : Stratification thermique obtenue avec des parois de faible émissivité pour différents AT
(Djanna F. et al., 2008).

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 30

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

On constate, sur cette figure, que comme dans la configuration précédente et quel que soit l'écart de température entre les parois actives, l'évolution de la température reste linéaire au coeur de la cavité. On note également la centro-symétrie des profils de température caractéristique de ce type de configuration. Les résultats obtenus sont reportés dans le tableau ci-dessous. L'étude d'incertitude montre que l'erreur commise sur ce paramètre ne dépasse pas 8 %. On peut donc conclure que le paramètre de stratification thermique est indépendant de l'écart de température.

Tableau 2 : Paramètre de stratification avec rayonnement faible des parois passives. (Djanna F. et

al., 2008)

LT(K)	10,0	15,0	17,4	20,0
Ra	5,8.10^10	8,6.10^10	1,0.10^11	1,2.10^11
S	0,59	0,57	0,56	0,54

En comparant les résultats, il ressort l'influence du rayonnement des parois « passives » sur la stratification thermique.

Figure 22 : Stratification thermique pour ?T=10, 15, 17,4 et 20 K. (Djanna F. et al., 2008)

On peut remarquer que, dans tous les cas, l'augmentation de l'émissivité fait baisser le paramètre de stratification. Ceci peut s'expliquer par l'influence du rayonnement des parois actives qui n'est pas négligeable et intensifie les écoulements secondaires. Ainsi, l'augmentation du rayonnement à l'intérieur de la cavité se traduit par des écoulements secondaires non négligeables

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 31

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

entraînant ainsi une homogénéisation de la température dans toute la cavité (y compris au coeur) et réduisant ainsi le gradient vertical de température. Ceci est observé sur tous les essais réalisés par (Djanna F. et al., 2008), puisque le paramètre de stratification passe de 0,57 dans le cas où le rayonnement des parois passives est faible (E = 0,10 #177; 0,05) à 0,45 lorsque ce rayonnement devient plus important (E = 0,60 #177; 0,02) soit une diminution d'environs 22%. Ces résultats sont à rapprocher de ceux obtenus par Salat J. [2008], qui présente une diminution de l'ordre de 30 % lorsque l'émissivité passe de 0,10 à 0,95 (0,72 Ô 0,54) avec un rapport de forme horizontal proche du cas étudié ici.

Le tableau suivant rassemble les résultats expérimentaux obtenus pour différentes configurations. Ce tableau confirme les observations précédentes, à savoir que pour une configuration géométrique donnée, la stratification diminue lorsque l'émissivité des parois passives augmente. L'étude des écoulements devrait permettre de confirmer les résultats thermiques, c'est-à-dire la présence d'écoulements secondaires non négligeables lorsque l'émissivité des parois passives augmente. On note également l'influence des rapports de forme. En effet, il apparait dans ces travaux que si le rapport de forme vertical Av n'influence pas de manière significative le paramètre de stratification thermique, le rapport de forme horizontal Ah a quant à lui une influence notable sur la stratification en température. Ceci peut s'expliquer par un effet de confinement et des écoulements secondaires tridimensionnels qui ne sont plus du second ordre lorsque la géométrie de la cavité varie. Ces conclusions sont à modérer étant donné que les cavités étudiées ne sont pas de géométrie « atypique » (cavité aplatie par exemple).

Tableau 3 : récapitulatif de quelques configurations étudiées (Djanna F. et al., 2008)

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 32

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

Le rayonnement de paroi induit une modification des écoulements secondaires qui conduit à une modification de la stratification thermique de la cavité. La centrosymétrie qui traduit, en grande partie, la validité des hypothèses de Boussinesq est cependant bien conservée.

En somme, que ce soit le nombre de Rayleigh, le nombre de Prandtl, le rapport de forme ou le couplage convection-rayonnement, l?écoulement se trouve soit transformer soit modifier. Sans oublier une interdépendance entre les différents paramètres. Maintenant que nous avons montré cette influence nous pouvons aborder plus en profondeur les configurations les plus utilisé dans la littérature.

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 33

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

CHAPiTRE II. DESCRIPTION DU PROBLEME ET

FORMULATION MATHEMATIQUE

Dans ce chapitre nous allons faire une description succincte et précise du problème que nous nous proposons de résoudre, dans le cadre de ce mémoire de master. En présentant le model expérimental sur lequel nous allons nous basé pour validé notre étude numérique (sachant pertinemment que le numérique ne peut se faire sans l?expérimentale). Ensuite nous allons poser les équations mathématiques (adimensionnelles et non adimensionnelles) qui régissent le système. Et enfin présenter la méthode de résolution numérique utilisée par le logiciel FLUENT pour déterminer cette évolution de température.

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 34

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

II.1 Description du problème physique

Le modèle physique considéré est présenté sur la figure 23. Il s'agit d'une cavité carrée

différentiellement chauffée dont les quatre parois internes sont supposées grises, diffuses, opaques et les surfaces sont supposées adiabatiques et ont la même valeur d'émissivité, å. Les parois

verticales sont isothermes et maintenues à un écart de température constante (T_c pour la paroi
chaude, et Tf pour la paroi froide). Les parois hautes, basse avant et arrière sont isolées. La cavité 2D est remplie d'un fluide transparent de l'air (Pr = 0,71), et le mouvement d'air est gouverné par les équations de Navier Stokes sous l'hypothèse de Boussinesq.

De manière classique, sans rayonnement de surfaces, la condition adiabatique implique que le gradient de température normal à ces parois est nul. En présence du rayonnement elle est traduite par l'équilibre entre les flux convectif et radiatif. Il s'est avéré que le rayonnement de surfaces ne modifie pas les équations gouvernant le mouvement du fluide mais altère seulement les conditions aux limites thermiques. Le couplage de la convection naturelle avec le rayonnement de surfaces se fait uniquement à travers les conditions aux limites thermiques.

Figure 23 : représentation de la cavité différentiellement chauffée avec conditions aux limites
thermiquesde 0,335 x 0,335 m (Wang H. et al., 2006)

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 35

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

II.2 Mise en équation

II.2.1 Formulation mathématique II.2.1.1 Hypothèses simplificatrices

Les équations présentées dans cette partie sont basées sur des hypothèses qu'il convient de rappeler :

> l'écoulement est stationnaire ;

> le fluide est supposé newtonien ;

> la variation de la masse volumique n'est considérée que dans le terme de la poussée thermique d'Archimède et elle est supposée constante (égale à ñ0) pour les autres termes des équations : c'est l'hypothèse de Boussinesq ;

> le volume reste constant sous l'action d'une pression externe (fluide isovolume), alors que sa masse volumique varie linéairement telle que p = po[ 1 -- fJ(T -- To)] où fJ est le coefficient d'expansion thermique et po la masse volumique à la température de référence To définie par :

;

> la seule source interne d'énergie est celle issue du bilan local entre l'absorption et l'émission volumique du rayonnement au sein du fluide.

Nous avons --A +qr= et A +qr= en z = H, où ë = 0.025 W/ (K m) est la

conductivité de l'air, T est la température et q_r est la densité de flux net radiatif. q_r est déterminée par les systèmes d'équations : qr =E1 _E (6T 4 -- J) et AJ = b où æ est la constante de Stefan- Boltzmann, J représente le vecteur radiosité, A la matrice dont ALS = 8 , -- (1 -- e)F11 avec Fij le

facteur de forme et b (b1 = ea Th le vecteur émission propre.

En convection naturelle les équations sont classiquement rendues sans dimension. Pour cela nous utilisons l'écart de température entre les parois actives OT et la température moyenne T0 pour définir une température réduite 0 = (T -- T_o)/OTT et, comme longueur et vitesse de référence, respectivement la hauteur H et áRa^1/2/H avec á la diffusivité thermique de l'air et Rah =

3

(gfJ T H )/(v ) le nombre de Rayleigh. Nous poursuivons cette logique pour rendre sans dimension les équations du problème avec rayonnement, à savoir que q_r et J sont rendues sans dimension par AOT /H, comme la définition du nombre de Nusselt en convection naturelle pure. Notons que le problème avec rayonnement fait apparaître conventionnellement deux paramètres sans dimension additionnels, outre Ra et Pr, le rapport de température, B_o = T_o/OT , et le nombre de rayonnement, Nr = ea Tô H/(AOT ) (ou son inverse le nombre de Planck). Comme il est difficile de faire varier un nombre sans dimension en maintenant constants les trois autres en

Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell Phidelo Page 36

« Etude de la convection naturelle turbulente dans une enceinte à paroi chauffé »

couplage convection naturelle-rayonnement, nous n'avons pas jugé nécessaire de faire apparaître è0 et Nr dans cette étude outre la mention de T0, T et H.