III-40
?
Dans l'équation de quantité de mouvement, le
terme du dénominateur ap Wp est remplacé
par ap Vp où Vp est la vitesse maximale
au niveau de la cellule P.
III.2.5 Etapes de la simulation numérique
En guise de rappel, soulignons que dans ce travail, la situation
physique correspond à un
écoulement naturel bidimensionnel, turbulent
incompressible dans une cavité ou nous avons impose
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 51
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
un écart de température entre les parois
verticales, et les parois horizontales sont supposé adiabatique. La
cavité a les dimensions HxlxD = 3,84m x 1m x 0,86m. Les
différentes étapes pour réaliser cette simulation
numérique (c'est-à-dire le passage du domaine physique au domaine
numérique) sont énumérées ci-après :
1ère étape : Maillage du domaine
physique
Le premier travail à accomplir dans la
réalisation d'une simulation numérique est la définition
d'un maillage adapté au problème physique après l'avoir
esquissé. De sa qualité dépend la précision des
calculs.
Un nombre de mailles insuffisant fera par exemple diverger le
calcul ou sera responsable d'une diffusion numérique trop importante
tandis qu'un maillage trop fin alourdira le calcul ou peut causer des
variations trop grandes dans les grosseurs de maille à travers le reste
du domaine. Il faut donc trouver un compromis entre les deux situations.
Le logiciel Gambit, est le préprocesseur dont nous
disposons. Nous avons utilisé un maillage régulier avec des
cellules de forme quadrilatérale. Un raffinement des zones au voisinage
de la paroi a été pris en compte pour ressortir les
différents phénomènes qui peuvent intervenir dans ces
zones, notamment les gradients de température et de vitesse.
Le résultat de la discrétisation des
équations différentielles de transport est un ensemble
d'équations algébriques. Nous avons donc divisé le domaine
de calcul en N mailles suivant x et en M mailles suivant r, nous aurons donc un
système de M x N d'équations algébriques non
linéaires pour chaque variable considérée. Après
avoir achevé cette étape, il faut exporter le domaine
maillé vers le solveur FLUENT.
2ème étape : Exportation du domaine et
spécifications des conditions initiales
Une fois importé le domaine maillé dans FLUENT,
on peut vérifier le maillage pour détecter d'éventuelles
erreurs qui pourrait fausser le calcul, le lisser s'il le faut et ensuite
préciser l'échelle du domaine physique étudié.
Ensuite il faudra choisir avec délicatesse et en fonction du
problème étudié, les modèles à utiliser
à savoir :
Le type de solveur pour la résolution des
équations (solveur découplé pour une résolution
séquentielle individuelle des équations ou solveur
couplé), la dimension du domaine (2D, axisymétrique, 3D...) ainsi
que le régime d'écoulement (permanent ou non);
Les modèles de fermeture du système
d'équations. Le code FLUENT dispose des modèles à
viscosité turbulente à une équation (modèle de
Spalart-allmaras) et à deux équations (les variantes du
modèle k?) de fermeture, des modèles aux tensions de Reynolds et
la simulation des grosses structures (LES).
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 52
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
Les fonctions de parois pour traiter la turbulence près
des parois dont FLUENT propose sont: les fonctions standard de parois
(«Standard Wall-Functions''), les fonctions de parois non
équilibrées (Non-equilibrium wall-function'') et un
traitement amélioré des lois de parois («Enhanced wall
treatment'').
Enfin, il faut fixer les conditions initiales qui sont
l'état de base du modèle à l'instant où la
simulation commence. Ici on évalue les propriétés
thermophysiques du fluide en écoulement ainsi que celles de la paroi en
contact avec le fluide à l'instant initiale (c'est-à-dire
à la température de référence pour le cadre de ce
travail et le flux de chaleur sur les parois). On pourra aussi définir
la valeur de la pression si l'on travaille à pression imposée et
l'accélération si la poussée d'Archimède ou
l'hypothèse de Boussinesq est considérée.
3ème étape : Spécification des
conditions aux limites
Le choix des conditions aux limites est une étape
déterminante dans un tel travail. Plusieurs types de conditions aux
limites existent. Nous utiliserons essentiellement la condition au limites
« wall » est une condition de flux de chaleur constant sur les parois
verticales de la conduite. Notre écoulement est délimité
par des parois imperméables et le fluide d'essai est de l'air, donc un
fluide supposé compressible.
4ème étape : Résolution proprement
dite des équations
Pour la résolution proprement dite des équations
qui gouvernent le problème, on procède comme suit dans FLUENT
:
y' Choix du facteur de relaxation pour chaque équation
;
y' Choix des schémas de discrétisation spatiale des
termes convectifs présent dans ces équations
y' Choix de l'algorithme de résolution pour le
problème de couplage pression-vitesse ; y' Choix des critères de
convergence ;
y' Exécution du calcul itératif.
Une fois la résolution effectuée nous pouvons
visualiser les champs de vitesse, de
température, de pression, de turbulence sur tout le
volume du domaine et aussi tracer différentes courbes
souhaitées.
En définitif, rappelons que dans la simulation
numérique de l'écoulement d'un fluide, on résout au moyen
d'un ordinateur, les équations préalablement
discrétisées suivant un schéma numérique. La
difficulté est liée à la physique du problème
traité, c'est-à-dire à la turbulence et le choix de
l'utilisation d'une méthode numérique va dépendre
essentiellement du type et de la
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 53
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
complexité du problème à résoudre
: la nature du fluide, le comportement thermodynamique, la modélisation
du milieu et l'aspect stationnaire ou instationnaire problème.
La figure ci après, résume, les étapes
à franchir pour simuler l'écoulement du fluide avec le code de
calcul industriel FLUENT.
1ère étape : Définition et
maillage du domaine physique
2ème étape : importation du domaine
physique maillé et définition des conditions
initiales
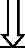
3ème étape : spécification des
conditions opératoires et des conditions aux limites
4ème étape : résolution proprement
dite des équations
5ème étape : visualisation et traitement
des résultats
Figure 25 : démarche de
simulation avec Gambit-Fluent
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 54
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
CHAPiTRE IV. RESULTATS ET DISCUSSION
L'objectif de ce paragraphe est de présenter dans un
premier temps l'influence du nombre de Rayleigh et de
l'émissivité des parois sur le paramètre de stratification
thermique. Ensuite, une comparaison de la stratification thermique dans des
cavités différentiellement chauffées expérimentales
est effectuée. Nous présentons les résultats obtenus lors
de notre simulation numérique réalisée avec le code de
calcul industriel FLUENT, sur un ordinateur de 2,30 x 2,29 GHz de
fréquence et de 2Go de capacité de mémoire.
L'approche « segregated solution method » (solveur
découplé) a été choisie pour la résolution
des différentes équations. Les termes de diffusion correspondant
aux équations de quantité de mouvement et de turbulence sont
discrétisés en utilisant le schéma de
discrétisation « Upwind » du second ordre et un critère
de convergence de 10-8 est adoptée Pour toutes les
équations. A cause du couplage et de la non linéarité des
équations, la stabilité du processus itératif est
assurée par l'utilisation de coefficients de sous relaxation. Pour
traiter la turbulence près des parois, l'approche «Standard
Wall-Functions'' est utilisée. La convergence du calcul numérique
est contrôlée par l'examen de l'évolution des
résidus relatifs à chacune des équations.
L'écoulement du fluide à l'intérieur de la cavité
dont la paroi est chauffée uniformément par un flux de chaleur
est contrôlé par les nombres adimensionnels suivants :
? Le nombre de Rayleigh (Rah), correspondant au rapport entre
les forces de pesanteur et les forces de diffusion de chaleur et frottements
visqueux ;
? Le nombre de Prandlt (Pr), (exprimant le rapport entre la
diffusivité de quantité de mouvement et la diffusivité
thermique);
? Le nombre de Nusselt (Nu), relatif aux taux d'échange
de chaleur paroi- fluide, est le rapport de la résistance thermique de
conduction par la résistance thermique de convection. Il est d'autant
plus élevé que la convection est prédominante sur la
conduction. Il caractérise le type de transfert de chaleur.
Apres avoir valide le model, nous présentons les
différents résultats obtenus. Les champs thermiques et dynamiques
et les profils de température et vitesse adimensionné tout au
long des parois sont mises en forme grâce au logiciel Tecplot 8.0.
Rédigé et soutenu par TIENTCHEU NSIEWE Maxwell
Phidelo Page 55
« Etude de la convection naturelle turbulente dans
une enceinte à paroi chauffé »
| 


