Problèmes du couplage hydromécanique des sols. Cas de la consolidation unidimensionnelle de Terzaghi dans un calcul par la méthode des éléments finis

3.7. - Analyse de la résolution au niveau de l'assemblage des éléments.

Dans le chapitre 2, nous parlions des hypothèses approximatives de Terzaghi. Dans sa théorie

k yw

et mv sont constants. Il les couple pour donner

k cv = , une constante. mv yw x

Découplons le coefficient de consolidation c de l'équation classique de Terzaghi pour voir son comportement dans la résolution par élément finis.

ô2 u ô u

t

cv ôu2 -->Equation classique ? dtx c_v[K}[ui}+[M}[ui}=[MXui-1} (3. 26)

Mémoire de Master 24 Yamné A.K. KOUAMA

UFR/SI

2u ?u ? Équation découplée - dt? k ?K??ui}+mv~M??ui??mv?M??ui?1?

y_w

k ?

?

m_v

t

2

?

?u

y_w

(3. 27)

Soit:

?Kk? ? c_v?K? ou ? ? ? K?

k

Kk ? (3. 28)

y_w

et ?M_m? ? ? M? ou?M_m? ? m_v?M? (3. 29)

Considérons un massif de sol avec deux sous couches dont les caractéristiques sont les suivantes: Tableau 3. 1.-Paramètres de deux couches différentes d'un sol

c

ki h m

~~

Couche 1	1	1	1	1
Couche 2	10	1	10	1

La résolution pour l'équation classique de Terzaghi donne:

?? 1 ? 1 ?

? ? ? ?

Kk ₁ Kk 2

? ? (3. 30)
?? ? 1 ?1??

?M _m?₁??M m?2 6??1 2 1 ?2 ? (3. 31)
J

L'assemblage donne:

(3. 32)

(3. 33)

? 1

K k ? ? ?1 ? ? ? ? ? 0 ?2 1 ? 1 M m ? ? ? 6 ? ? ? 0

?1 2 ?1 1 4 1

0? ?1 ? ? 1 ?? 0? 1 ? ? 2??

La résolution pour l'équation découplée donne:

?? 1 ?1?

? ?

Kk ? (3. 34)
1 ?? ? 1 ? 1??

Mémoire de Master 25 Yamné A.K. KOUAMA

UFR/SI

??10 ?10?

? ?

K k ? (3. 35)
2 ?? ? 10 ? 10 ??

1 ? 2 1 ?

? ?

M m ? (3. 36)

1 6 ??1 2 ??

1?20 10?

? ?

M m ? 10 20 (3. 37)

2 6 ?? ??

L'assemblage aboutit à :

? ? K k	? 1 ?1 0? ? ? ? 1 11 10 (3. 38) ? ? ? ? ? ? 0 ?10 10??
? ? M m		? 2 1 0? 1 ? 1 22 10 ? ? (3. 39) 6 ? ? ? ? 0 10 20??

Clairement on voit que nous n'aboutissons pas aux mêmes matrices. Ce qui implique que la surpression interstitielle qui sera déterminée ne sera pas pareille quand bien même nous avons le même coefficient de consolidation c, = 1. La conclusion qui découle de cette partie c'est que la consolidation de Terzaghi par éléments finis n'est pas appropriée pour le calcul dans les sols multicouches.

3.8. - Solution exacte de l'équation et solution par éléments finis

La solution exacte de la consolidation unidimensionnelle est obtenue par la résolution analytique. La solution par la loi de Fourier donne :

2

2

u z t u z t

e ? ?

( , ) ? ( ,0) c_v )

( (3. 40)
z

La résolution numérique donne une solution approchée de l'équation. Avec l'analyse sur les erreurs qui pouvaient survenir il est important de voir comment cette résolution se comporte vis-à-vis de celle exacte. La recherche bibliographique (fig3.6) nous donne les évolutions à différents temps de la surpression interstitielle.

Mémoire de Master 26 Yamné A.K. KOUAMA

UFR/SI

Fig. 3. 6 : Comparaison de l'évolution de la surpression interstitielle dans un calcul par

éléments finis (FEM) et la solution exacte de l'équation (Terzaghi) (MOHAMAD et al, 2012)

Il apparait que les deux solutions ont la même allure et se superposent quasiment. En plus la

représentation du degré de consolidation en fonction du facteur temps (fig3.7) nous conforte dans nos propos vue la bonne superposition qu'elle représente.

Mémoire de Master 27 Yamné A.K. KOUAMA

UFR/SI

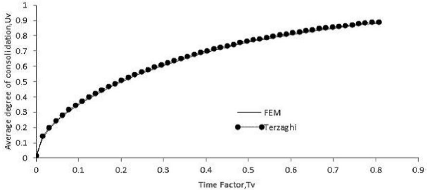
Fig. 3. 7 : Comparaison de l'évolution du degré de consolidation moyenne (MOHAMAD et

al, 2012)

Maintenant si nous prenons le cas du calcul pour les sols multicouches, nous voyons que la figure 3.8 nous donne des courbes différentes.

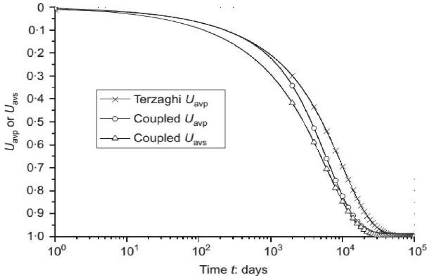
Fig. 3. 8 : Comparaison de l'évolution du degré de consolidation moyenne pour les sols
multicouches (HUANG et al, 2010)