Problèmes du couplage hydromécanique des sols. Cas de la consolidation unidimensionnelle de Terzaghi dans un calcul par la méthode des éléments finis

UNIVERSITÉ DE THIES

UNITE DE FORMATION ET DE RECHERCHES

SCIENCES DE L'INGENIEUR

Laboratoire de Mécanique et Modélisation

Année : 2012/2013

MEMOIRE DE MASTER

Mécanique des Sols - Géotechnique & Modélisation des Terrains

Présenté par :

Yamné Abdoul Kader KOUAMA

Problèmes du couplage hydromécanique des sols :

cas de la consolidation unidimensionnelle de

Terzaghi dans un calcul par la méthode des

éléments finis

Soutenu le 20 novembre 2013 devant le jury composé de :

Président

Meissa FALL Université de Thiès, UFR SI

Examinateurs

Mapathé NDIAYE Université de Thiès, UFR SI

Mathioro FALL Université de Thiès, UFR SI

i

Avant-propos

Je souhaite remercier tous ceux qui, par leur aide et leurs encouragements, m'ont permis de réaliser ce travail.

Je tiens à exprimer ma profonde gratitude au Professeur Meissa FALL, Directeur de l'UFR -SI, pour la confiance qu'il m'a accordée en m'acceptant dans son établissement.

Je tiens également à remercier tous les responsables de l'université de Thiès, pour m'avoir offert cette agréable opportunité d'intégrer l'univers de la recherche scientifique et d'y faire mes premiers pas.

Abib TALL, Adama DIONE merci pour la documentation et l'encadrement qui m'ont permis de comprendre et de rédiger ce mémoire.

A ma famille, mes amis, je tiens juste à leur dire MERCI

Enfin, je souhaite une bonne continuation à toute la promotion 2012/2013 du Master Recherches.

ii

SOMMAIRE

Avant-propos i

Liste des notations et des abréviations iv

Résumé vi

Introduction générale 1

Chapitre 1.- Revue bibliographique : La consolidation, un comportement hydromécanique 2

1.1. - Introduction 2

1.2. - Le tassement 2

1.3. - Phénomène de consolidation 3

1.4. - Théorie de la consolidation unidimensionnelle de Terzaghi 4

1.5. - La méthode des éléments finis et ses sources d'erreurs 5

1.6. - Conclusion 6

Chapitre 2 : Les limites de la modélisation de la consolidation unidimensionnelle de Terzaghi

		7
2.1. -	Introduction	7
2.2. -	Modélisation de la consolidation unidimensionnelle de Terzaghi	7
2.3. -	La validité de la loi de Darcy	10
2.4. -	La constance de la perméabilité	11
2.5. -	La compressibilité du fluide (eau + gaz)	12
2.6. -	L'homogénéité des sols	12
2.7. -	La relation linéaire entre l'indice des vides et la contrainte effective	12
2.8. -	La consolidation unidimensionnelle	13
2.9. -	L'importance de la compression secondaire	14
2.10. -	Conclusion	14

Chapitre 3 : Les difficultés de la résolution numérique par éléments finis de la consolidation

unidimensionnelle de Terzaghi 16

3.1. - Introduction 16

3.2. - Discrétisation en espace de la consolidation unidimensionnelle et fonction

d'interpolation 16

3.3. - Discrétisation en temps 17

3.4. - Résolution numérique 18

3.5. - Résolution numérique adimensionnelle 20

3.6. - Analyse de la résolution pour les éléments situés aux limites perméables 22

iii

3.7. - Analyse de la résolution au niveau de l'assemblage des éléments. 24

3.8. - Solution exacte de l'équation et solution par éléments finis 26

3.9. - Conclusion 28

Conclusion générale et perspectives 30

Références bibliographiques 31

Table des matières 33

Listes des figures et tableaux 35

Annexes 36

iv

Liste des notations et des abréviations

u: surpression interstitielle de l'eau

c,,: coefficient de consolidation

k: coefficient de perméabilité

a,,: coefficient de compressibilité

m,,: compressibilité du sol

M: masse totale du sol

V: volume total du sol

Ms: masse du squelette solide

Mw: masse de l'eau (contenue dans le sol)

e: indice des vides

e0: indice des vides initial

n: porosité du sol

t: temps

z: la profondeur d'un point

A_s: masse volumique du squelette solide

A_w: masse volumique de l'eau

Vw: vitesse de l'eau dans les interstices

Vs: vitesse des grains solides

Q: Débit à travers la surface considérée

S: surface à travers laquelle s'effectue l'écoulement vertical

i: gradient hydraulique

h : charge hydraulique

y_w: poids volumique de l'eau

06v ou OQ : contrainte totale (charge) appliquée à la surface du massif de sol

06v^': contrainte effective verticale

H: la hauteur totale de l'échantillon

h: la hauteur/longueur d'un élément

v

T: facteur temps

Z: la hauteur adimensionnelle de l'échantillon

u : le degré de consolidation

uap : le degré de consolidation défini par la surpression interstitielle

uaS : le degré de consolidation défini par le tassement

vi

Résumé

Construire sur des sols fins demande à ce qu'on soit très regardant sur le phénomène de tassement. Un tassement qui se résume essentiellement au phénomène de consolidation. En 1923 Karl Terzaghi énonce la théorie de la consolidation unidimensionnelle par l'équation:

? 2	u ? u
cv ? ? u 2 ?		t

Cette équation est toujours utilisée de nos jours dans le calcul de tassement des ouvrages dont les dimensions des charges sont grandes par rapport aux épaisseurs des couches compressibles. Le but de notre travail c'est de montrer les problèmes de sa résolution par une méthode numérique d'actualité à savoir les éléments finis. La finalité étant de conforter ou réfuter cette méthode.

En résolvant l'équation nous trouvons que les éléments finis sont incapables de modéliser la condition initiale. Des erreurs apparaissent dans les premiers instants, une période initiale qui du reste est très courte par rapport à la durée réelle des phénomènes. Nous avons également montré que l'emploi du coefficient de consolidation c, n'est pas approprié dans les sols multicouches. Hormis cela, les résultats de la résolution par éléments finis se superposent à ceux exacts de la résolution analytique.

Mots-clés: couplage hydromécanique-consolidation unidimensionnelle-éléments finis

Introduction générale

La pérennité de tout ouvrage édifié sur le sol passe par une meilleure connaissance de ce sol. La stabilité vis-à-vis du tassement est une condition sine qua none pour tous les ouvrages au sol. Dans les sols fins le tassement se résume principalement à un tassement de consolidation. Le phénomène de consolidation étant un phénomène qui met en jeu un comportement hydraulique couplé à un comportement mécanique. De nombreux chercheurs ont travaillé sur ce phénomène. L'allemand Karl Terzaghi a, en 1923, énoncé une théorie de la consolidation unidimensionnelle. Elle est toujours utilisée de nos jours avec l'outil informatique à travers entre autre le calcul par la méthode des éléments finis. La résolution numérique par éléments finis est pratique et s'inscrit dans les contextes actuels de travail. La complexité du couplage hydromécanique va se répercuter sur le calcul de la consolidation. Quels sont les difficultés que pose le phénomène hydromécanique qu'est la consolidation, telle que définie par Terzaghi, dans un calcul par éléments finis? C'est la question autour de laquelle va s'articuler notre travail. La méthodologie consistera à analyser la théorie de consolidation de Terzaghi à travers les étapes de la méthode des éléments finis que sont la modélisation, la discrétisation et la résolution numérique.

Pour ce faire, le mémoire est organisé comme suit :

Un premier chapitre consacré à la revue bibliographique sur les concepts de base de notre sujet. Il y sera question du tassement, de ses composantes, du phénomène de la consolidation, de la théorie de Terzaghi et du principe de la méthode des éléments finis.

Un deuxième chapitre portant sur l'analyse de la modélisation de la consolidation de Terzaghi. Nous y reviendrons sur la modélisation et mettrons en lumière des limites dans ses hypothèses.

Un troisième chapitre où nous nous pencherons sur les difficultés de la résolution numérique par éléments finis de l'équation établie à la fin de la modélisation. Dans ce chapitre nous ferons la résolution numérique et ensuite analyserons les points particuliers que sont les éléments situés aux limites perméables et l'assemblage des éléments.

Une conclusion et des perspectives mettront fin au travail.

Mémoire de Master 1 Yamné A.K. KOUAMA

UFR/SI

Chapitre 1.- Revue bibliographique : La consolidation, un comportement
hydromécanique

1.1. - Introduction

Les sols sont des milieux poreux constitués d'un squelette déformable, d'un fluide (ou plusieurs) éventuellement compressible qui de plus peut s'écouler au travers de la porosité. Les sols sont hétérogènes et leur comportement mécanique complexe peut être affecté de manière très significative en présence d'eau : c'est le cas des sols fins. Pour Yves Berthaud et al (2008) il est donc essentiel de ne pas dissocier comportement hydraulique et comportement mécanique du sol afin de bien mettre en évidence les couplages forts qui existent entre ces deux phénomènes : on parle de couplage hydromécanique dans les sols.

La consolidation met en jeu clairement la question du couplage hydromécanique. Pour mieux comprendre ce fait, il est impératif de le situer dans le phénomène plus global qu'est le tassement. Par la suite nous allons nous appesantir sur la consolidation proprement dite, puis sur la théorie de la consolidation unidimensionnelle de Terzaghi pour terminer sur le principe de la méthode des éléments finis.

1.2. - Le tassement

Le sol, comme tous les autres matériaux, se déforme lorsqu'on lui applique une charge. Un sol soumis à une sollicitation externe se comprimera. Si les dimensions de la zone chargée sont grandes par rapport à l'épaisseur de la couche, on peut admettre que les déformations au milieu de la zone chargée sont uniquement verticales, ces déformations sont appelées « tassement ».

Il se subdivise en trois composantes à savoir le tassement instantané, le tassement de consolidation primaire et le tassement de compression secondaire.

? Tassement instantané

Ce tassement est appelé aussi tassement initial ou compression élastique. Le tassement instantané correspondant à un premier réarrangement des grains du sol et la disparition des vides remplis d'air, jusqu'à saturation du sol. La modification de la structure du sol est identique à celle induite par le compactage. C'est pour éviter ces déformations que l'on soumet le sol au compactage. Ce tassement est le plus important dans les sols pulvérulents et souvent négligeables dans les sols fins.

? Tassement de consolidation primaire

Le tassement de consolidation est le déplacement vertical de la surface du sol correspondant à un changement de volume à n'importe quel stade du processus de consolidation. La consolidation primaire est la réduction graduelle du volume d'un sol complètement saturé, à faible perméabilité due au drainage de quelques quantités d'eau dans les pores. Cette action se poursuit jusqu'à ce que l'excès de pression interstitielle (u) dans les pores dû à une augmentation des

Mémoire de Master 2 Yamné A.K. KOUAMA

UFR/SI

contraintes totales (?Q), ait été complètement dissipé jusqu'au rétablissement de l'équilibre hydrostatique. Le tassement de consolidation est un phénomène qui dépend du temps ; il se produit dans les sols à grains fins qui présentent un faible coefficient de perméabilité. La vitesse de tassement dépend du taux de drainage de l'eau interstitielle. La consolidation primaire est donc un phénomène hydromécanique.

? Tassement de compression secondaire ou fluage

L'expérience montre que le sol continu à tasser une fois la consolidation primaire achevée. Elle est principalement due à l'arrangement graduel des particules. Elle est la composante la plus importante pour des sols comme les tourbes et ceux fortement organiques.

Dans le tassement nous allons nous intéresser à la consolidation primaire. De la connaissance de ce phénomène va dépendre la stabilité des ouvrages édifiés sur les sols fins vis-à-vis du tassement. Elle est la composante prépondérante dans les sols fins. Elle s'étale dans le temps et sa modélisation est complexe en raison des phénomènes couplés qu'elle implique. Le calcul et l'évolution du tassement pour les sols fins se fait généralement à partir de la théorie de consolidation unidimensionnelle de Terzaghi.

1.3. - Phénomène de consolidation

La consolidation (consolidation primaire) d'un sol est le phénomène conduisant à la dissipation des surpressions interstitielles et à la diminution du volume du sol au cours du temps sous les charges qui lui sont appliquées. Nous reprenons ici le principe du phénomène de consolidation explicité par Jean-Pierre Magnan (1988) :

? Le sol est chargé par l'intermédiaire d'une plaque percée d'un orifice de faible diamètre,

muni d'un robinet.

? Le comportement mécanique du squelette solide du sol est schématisé par un ressort.

? La phase liquide est représentée par de l'eau.

? La faible perméabilité du sol est simulée en restreignant la section de l'orifice permettant

à l'eau de s'échapper à travers la plaque de chargement.

Fig. 1.1.- Modèle rhéologique de la consolidation (Magnan, 1988)

Mémoire de Master 3 Yamné A.K. KOUAMA

UFR/SI

? À l'instant initial (a) t = 0 (robinet fermé), la charge appliquée à la plaque est transmise

intégralement à l'eau, le ressort n'est pas sollicité.

? Après ouverture du robinet (b), l'eau s'échappe lentement au cours du temps, la charge est
reprise progressivement par le ressort.

En fin de consolidation (c), la surpression dans l'eau est dissipée, l'écoulement s'arrête et la charge est entièrement transférée sur le ressort. Le Tableau 1.1 nous donne l'évolution des différentes contraintes pendant la consolidation.

Tableau 1.1- Evolution des contraintes au cours de la consolidation (Magnan, 1988)

1.4. - Théorie de la consolidation unidimensionnelle de Terzaghi

La théorie de la consolidation unidimensionnelle développée par Terzaghi en 1923 traite de la consolidation d'une couche de sol fin saturé dans laquelle les déformations et les écoulements sont uniquement verticaux et où la charge uniforme et semi-infinie est appliquée instantanément à l'instant initial. Elle correspond aux conditions de l'essai oedométrique sous chaque palier de chargement, et au schéma des couches de sols compressibles sans déplacements horizontaux. Une représentation de cette configuration est comme suit :

Fig. 1. 2.- Définition des couches de sols et du chargement (Terzaghi, 1923) La théorie de Terzaghi repose sur les hypothèses suivantes:

? La couche de sol compressible est homogène et saturée complètement;

? L'eau et les grains de sol sont incompressibles;

? La loi de Darcy s'applique;

Mémoire de Master 4 Yamné A.K. KOUAMA

UFR/SI

· La compression est unidimensionnelle ;

· L'écoulement de l'eau est unidimensionnel;

· Les déplacements sont faibles;

· Le coefficient de compression a, et le coefficient de perméabilité k sont constants pendant la consolidation ;

· La contrainte effective et l'indice de vide sont linéairement proportionnels.

Avec ces hypothèses l'équation de la consolidation unidimensionnelle de Terzaghi s'obtient en combinant les équations de conservation de la masse de l'eau et de la masse des grains solides, la loi de Darcy (hydraulique) et la loi de compressibilité du squelette ( mécanique), écrit sous forme unidimensionnelle.

? 2		u ? u		Cv = ? u 2 ?
t

Avec :

k

C_v = : le coefficient de consolidation. Sa valeur numérique est fonction de la
m_v Y_v

x

perméabilité k, du coefficient de compressibilité du sol m, et du poids volumique de l'eau Y_w. .Le coefficient de consolidation est toujours supposé constant pour simplifier les calculs.

c, étant considéré constant, l'équation de Terzaghi est une équation aux dérivées partielles du second ordre à coefficient constant.

1.5. - La méthode des éléments finis et ses sources d'erreurs

La méthode des éléments finis est une méthode qui consiste à remplacer la structure physique à étudier par un nombre finis d'éléments ou de composants discrets qui représentent un maillage. Ces éléments sont liés entre eux par un nombre de points appelés noeuds. On considère d'abord le comportement de chaque partie indépendante, puis on assemble ces parties de telle sorte qu'on assure l'équilibre des forces et la compatibilité des déplacements réels de la structure en tant qu'objet continu. Elle permet d'étudier correctement des structures continues ayant des propriétés géométriques et des conditions de charges compliquées. Elle nécessite un grand nombre de calculs qui, à cause de leur nature répétitive, s'adaptent parfaitement à la programmation numérique. La résolution numérique donne une solution approchée du problème étudié. La solution calculée est entachée d'erreurs. Erreur n'est pas à prendre au sens de la faute mais d'une imprécision inévitable. La résolution d'un problème par éléments finis se déroule en trois phases :

· La modélisation.

· La discrétisation

· La résolution numérique

Mémoire de Master 5 Yamné A.K. KOUAMA

UFR/SI

1.6. - Conclusion

La consolidation unidimensionnelle de Terzaghi est utilisée dans les calculs de tassements sur les sols fins pour des ouvrages tels que les remblais, les radiers.... Son équation est la conjugaison des équations de conservation de masse, de l'équation mécanique de la compressibilité du squelette et de l'équation hydraulique de l'écoulement de l'eau dans le sol. Pour sa résolution de l'équation il existe plusieurs méthodes: la résolution analytique (solution exacte) et numérique (solution approchée : les différences finis, les éléments finis..). La complexité du couplage hydromécanique du phénomène va entrainer des difficultés dans la résolution par la méthode des éléments finis. Des problèmes aussi bien au niveau de la modélisation que de la résolution numérique que nous verrons dans les parties qui suivront.

Mémoire de Master 6 Yamné A.K. KOUAMA

UFR/SI

Chapitre 2 : Les limites de la modélisation de la consolidation
unidimensionnelle de Terzaghi

2.1. - Introduction

La théorie de consolidation unidimensionnelle de Terzaghi établie en 1923 est jusqu'à nos jours utilisée pour le calcul et l'évolution du tassement dans les sols fins. La consolidation met en jeu un couplage fort qui existe entre la compressibilité mécanique du squelette et le drainage de l'eau. Pour modéliser ce couplage Terzaghi a fait recours à de nombreuses hypothèses. La résolution par éléments finis nous implique nécessairement de nous appesantir sur la modélisation du phénomène. Il ne sert à rien de trouver la solution exacte d'une équation qui n'est pas représentative du phénomène physique. La finalité étant de mieux appréhender la consolidation, nous allons dans ce chapitre revenir sur le processus de l'établissement de l'équation de Terzaghi, puis analyser au cas par cas ses hypothèses pour relever les limites et les insuffisances éventuelles.

2.2. - Modélisation de la consolidation unidimensionnelle de Terzaghi

s La conservation de la masse :

On considère un massif de sol saturé de volume y et de masse M. La consolidation intervenant après le tassement instantanée, correspondant à l'expulsion des poches d'air, on a par principe un échantillon saturé. Dans cet échantillon on a deux phases: solide et liquide donc M = Ms + Mw. L'application de la conservation de masse pour cet élément s'écrit:

?

?

?

??

0

dM

dt

d(Ms

0

?

Mw)

(2.1)

L

dt

Du fait que les masses de l'eau et des grains solides ne peuvent pas avoir des variations négatives l'équation (2.1) implique que :

dMs dt

dMw

= 0 et = 0 (2. 1)
dt

Par définition la masse de l'eau dans cet échantillon est :

Mw=??v? n

w (2. 2)

Soit:

Mémoire de Master 7 Yamné A.K. KOUAMA

UFR/SI

dMw dnv? d ? ( ? n)

w w

? ? ?? nvdv?? ? dv? ?? nVw?dS (2. 3)

w w

dt dt dt t

v v s

Par application du théorème de la divergence à l'égalité (2.4) on obtient :

^???_?div(? _wnVw) ? w )

t

?

?

?

dv?0 (2. 4)

?

v

?

(

n

Dans les hypothèses de Terzaghi l'eau étant incompressible, c'est-à-dire pu^, = constante, l'equation de conservation de l'eau s'écrit finalement :

??( n )? ? ?( n) ?

? div(nVw)? ?0? ( )? ?0 (2. 5)

w?? ? ?? ?? div nVw

t ? t ??

Par définition la masse des grains solides dans l'échantillon est :

Ms ? ? ? (1? n) v

s (2. 6)

En suivant le même cheminement et toujours dans les considérations de Terzaghi, incompressibilité des grains solides, on obtient l'équation suivante pour la conservation de masse des grains solides:

??(1 ? n) ? ? ? (1 ? n) ?

? div((1? n)Vs) ? ?0 ? ((1 ? ) ) ? ? 0 (2. 7)

s ?? ? ?? ?? div n Vs

t ? t ??

Les déformations étant supposés unidimensionnelles, la conservation de la masse de l'échantillon est :

?(1

? n Vs

) ( ) ?
?nVw

? 0 (2. 8)

? z ? t

? La loi de Darcy

Par définition la vitesse apparente est :

Q S

? Vw (2. 9)

La vitesse relative de l'eau par rapport aux grains solides est :

Q

Vw ? Vs ? (2. 10)
nS

La loi de Darcy sur l'écoulement hydraulique est :

Q ? Ski (2. 11)

Mémoire de Master 8 Yamné A.K. KOUAMA

UFR/SI

Avec le gradient hydraulique i ? ?gradh (2. 12)

u

Et la charge hydraulique dans les sols h? ? z (2. 13)

y_w

Finalement on a :

?(u ?y_wz)

(2. 14)

Vw ? Vs	? ?		k
		n	yw

?z

? La loi de compressibilité

Pour Terzaghi, la variation de l'indice des vides est linéairement proportionnelle à la contrainte effective. Soit :

de??a vd?? Etant donné que :		(2.		15)	d?? ? d(??' ?u)? 0
	(2.	16)		Alors :
				d??^'? ?du
	(2.	17)		Soit:
				de ? avdu
	(2.	18)		? Ecriture de l'équation de la consolidation
				On sait que:
				e
?e	(2.	19)
? (1 e)^2
				En remplaçant la valeur de n dans l'équation de conservation de masse on trouve :
				Vs
				Vw ? ? e
	(2.	20)		La loi de Darcy devient donc :
				k ?(u ?ywz)
	(2.	21)
Vw? eVw ? ?
n yw ?z

Mémoire de Master 9 Yamné A.K. KOUAMA

UFR/SI

Et on tire:

k

?_w

?

(u

y z)

?

Vw

n(1?e)y_w ?z

(2. 22)

En remplaçant V w par son expression dans l'équation de conservation de masse de l'eau on a :

? ? k ?(u)? ?n

? ? ? (2. 23)

?z? n(1?e) y_w ?z ? ?t

? ?

?

n ?t

Dans cette équation on introduit l'expression de

?e

? ? k ?(u)?_? ?t ? a_v ?u

(2. 24)

?z? n(1?e)y_w ?z ? ? ? ?t

? ? (1 e)² (1 e)²

? (1 )

? ? e k ?u? ?u

? ? ? (2. 25)

?z ? avyw ?z ? ?t

? ?

Terzaghi pose	cv	(1? e)k ? et considère que la perméabilité k et le coefficient de compression
av			yw

a sont des constantes. L'équation de la consolidation unidimensionnelle s'écrit donc :

_?2

t

u ?u

c_v ?

? u 2 ?

(2. 26)

2.3. - La validité de la loi de Darcy

En 1856 Henry Darcy énonça la loi d'écoulement dans les sols (2.12):

v ? ki

v: la vitesse d'écoulement du fluide dans le sol

De nombreuses références prouvent de façon quasi certaine la validité de la loi de Darcy pour la plupart des écoulements dans les sols dont les dimensions vont du sable moyen au limon. Cependant des déviations de la loi de Darcy ont été relatées dans les sols aux grains de dimensions extrêmes. En effet des recherches ont montré des déviations du comportement prévu dans le cas des argiles et des sols argileux. Parmi ces recherches on peut citer Izbash, (1931), Lutz et Kemper (1959), Hansbo(1960); Miller et Low (1963), Mitchell et Younger (1963), Gardner et al (1974), Zou (1990). Ces déviations constatées sont de deux ordres :

Mémoire de Master 10 Yamné A.K. KOUAMA

UFR/SI

s Gradient seuil apparent : en dessous duquel le flux est soit nul (l'eau reste apparemment

immobile) soit au moins inférieur à celui prédit par la loi de Darcy

v ? 0 ou v ?ki (2. 27)

s Non linéarité de la loi de Darcy : la relation écoulement et gradient n'est pas linéaire en

d'autres termes la perméabilité n'est pas constante. Cette déviation de la linéarité est rapportée aux très faibles et très forts gradients (i<10 ou i>100).

Fig. 2. 1- Gradient seuil apparent et déviation de linéarité (Miller et Low, 1963)

En somme on doit noter que l'usage systématique que fait Terzaghi dans sa théorie de la loi de Darcy n'est pas vérifié pour tous les sols. La compréhension courante est que la loi de Darcy est valide tant que toutes les conditions environnementales restent inchangées : pas de changement de structure, pas de migration des particules, pas de température différentielle ou de changement dans la chimie de l'eau interstitielle, pas de variation de la contrainte effective. Des limites de loi de Darcy sont ressorties une limite sur la constance de la perméabilité au cours de la consolidation.

2.4. - La constance de la perméabilité

Les déviations montrées sur les figures 2.1 où les valeurs de la perméabilité semblent être fonction du gradient hydraulique, peuvent être attribuées aux migrations des particules à travers l'échantillon, menant au bouchage et au débouchage de vides selon Mitchell and Younger (1967). Mitchell (1976) nous apprend qu'une redistribution locale de l'indice des vides est susceptible de se produire si les particules qui ne participent pas au squelette qui supporte les efforts dus au chargement, sont délogées et transportées sous des valeurs modérées de gradient hydraulique entrainant une évolution de la perméabilité. On sait par ailleurs que la perméabilité hydraulique est fonction de la géométrie du réseau capillaire (porosité, tortuosité). Dans la formule dite de Kozeny Carman très utilisée pour les sols à l'exception des sols fins (argileux) pour lesquels d'autres phénomènes électro cinétiques interviennent on voit clairement le lien

Mémoire de Master 11 Yamné A.K. KOUAMA

UFR/SI

entre perméabilité et indice des vides. Etant donné que la consolidation est un changement de volume, variation de l'indice des vides, il apparait évidemment qu'elle s'accompagne d'une variation de la perméabilité au cours du temps suivant les couches. Ce qui veut dire exactement que :

?z

? ?

?

? ?

(1? e)k ?u? ? ?(1 ? e) ?u?

? ? k ? ? (2. 28)

?z ? ?z ? ? ?z

a_v

y_w

? avyw ??

A cela va s'ajouter le fait que le coefficient de consolidation ne peut pas rester constant tout au long de la consolidation.

2.5. - La compressibilité du fluide (eau + gaz)

Pour Bernard FÉLIX et al, (1981) les sols argileux compressibles contiennent toujours une certaine quantité de gaz qui, à la pression atmosphérique, se présente sous la forme de bulles de petit diamètre et en solution dans l'eau interstitielle. Le volume qu'il occupe change avec la pression du fluide interstitiel. Juste après le chargement d'un sol soumis à une compression drainée; sans contrepression, on observe une déformation quasi instantanée qui ne correspond à aucun volume drainé. Son importance n'est pas toujours négligeable devant les déformations de consolidation. Lorsque la phase gazeuse est discontinue et se présente sous forme de bulles d'air piégées dans l'eau par exemple, Xiang-Ling LI (1999) nous dit que la phase fluide (mélange d'eau et de bulles d'air) du sol se comporte comme un liquide très compressible. Cela implique que l'égalité établie en (2.6) n'est pas exacte :

?? _wn

? ?? div(? _wnVw) ? ?

?t

v

( )

? ? ? ?(n)?

dv ? ? ? (2. 29)

?? div(nVw)

w ? ??

? t

2.6. - L'homogénéité des sols

On rencontre rarement dans la nature des sites constitués par un sol compressible homogène et isotrope sur toute son épaisseur. Dans les travaux de Jean-Pierre MAGNAN (1988) il est écrit que par exemple, pour un sol de nature donnée constante, normalement consolidé, la pression de pré consolidation et l'indice des vides e0 varient avec la profondeur:

?(1 )

? ? e k ?u? ? (1 ? e)k ?u (2. 30)

?z? a_vy_w ?z? a_vy_w ?z

? ?

2.7. - La relation linéaire entre l'indice des vides et la contrainte effective

La courbe de compressibilité d'un sol c'est la courbe qui donne l'indice des vides en fonction de la contrainte effective. Le coefficient de compressibilité a est le rapport du changement d'indice des vides et de la variation de contrainte effective normale correspondant. La valeur du coefficient de compressibilité n'est pas une constante, elle décroît lorsque la contrainte effective

Mémoire de Master 12 Yamné A.K. KOUAMA

UFR/SI

augmente. Les travaux d'Arabet LEILA (2010) nous le démontrent. Toutefois, pour des petites variations de la valeur de contrainte, le coefficient a peut être considéré comme étant constant.

Hors dans sa théorie, Terzaghi établit une linéarité entre la contrainte et l'indice des vides .Les résultats de l'essai oedométrique (figure 2.2) montrent après simplification que l'indice de vide est linéairement proportionnel non pas à la contrainte effective, mais au logarithme de celle-ci. Pour cette linéarité on a pris l'habitude de représenter les variations de l'indice des vides en fonction du logarithme de la contrainte effective. L'égalité (2.16) n'est donc pas exacte:

de??_{a v}d?? (2. 31)

Echelle linéaire

Echelle logarithmique

Fig. 2. 2.- Allures des courbes de compressibilités (Magnan,1988)

2.8. - La consolidation unidimensionnelle

Dans le cadre de la théorie de Terzaghi on suppose que le drainage et les déformations sont uniquement verticaux. Des études de Bourges et Mieussens (1979) ont montré que pour la plupart des remblais, la déformation latérale différée est de l'ordre de 20% du tassement mesuré. L'erreur que l'on commet en calculant l'amplitude des tassements à partir d'une théorie unidimensionnelle est donc généralement admissible pour les ouvrages courants.

Davis et Poulos (1968) ont montré par exemple que, pour une fondation dont la largeur B est égale à l'épaisseur H de la couche compressible, supposée isotrope, le temps de consolidation est de 2,6 fois plus petit pour 40% de degré de consolidation et 2 fois plus petit pour 60% ,si le calcul est fait en tenant compte de la diffusion horizontale des surpressions interstitielles et non plus seulement de l'écoulement vertical. On voit donc que l'approximation de la dissipation unidimensionnelle des surpressions interstitielles conduit à une erreur importante, même pour des rapports B/H de l'ordre de 1. On conçoit par ailleurs que l'incidence sera encore plus importante si la perméabilité horizontale est supérieure à la perméabilité verticale, hypothèse couramment admise, compte tenu du mode de formation en strates horizontales, des couches de sols compressibles. Ces observations montrent qu'il était donc tout à fait justifié , sur un plan pratique, de mettre à la disposition de l'ingénieur un moyen de calcul permettant de tenir compte

Mémoire de Master 13 Yamné A.K. KOUAMA

UFR/SI

de la diffusion bidimensionnelle des surpressions interstitielles, tout en conservant le schéma du tassement unidimensionnel.

Fig. 2. 3.- Comparaison des temps de consolidation en fonction des considérations sur le sens de l'écoulement de l'eau (MIEUSSENS et al, 1980)

2.9. - L'importance de la compression secondaire

La compression secondaire ou fluage est le tassement qui se produit après qu'ait cessé toute surpression interstitielle. Elle est généralement négligée pour les sols fins du fait qu'elle soit mineure par rapport au tassement de consolidation. Mais D. Rousselot nous dit que ce tassement est d'autant plus important que le sol est plus organique. Pour certains sols, comme les tourbes ou les vases fortement organiques, cette compression secondaire représente une partie importante du tassement total du sol. De ce qui a été dit on voit clairement que pour ces sols la théorie de Terzaghi donnerait pour le calcul de tassement des erreurs forts remarquables, elle qui ne considère que le seul tassement de consolidation.

2.10. - Conclusion

Les hypothèses émises par Terzaghi pour modéliser le comportement hydromécanique qu'est la consolidation présentent des limites. Elles ne doivent être utilisés pour tous les sols fins (sols organiques, tourbes) ni à toutes les conditions (écoulement à fort ou faible gradient hydraulique par exemple). La modélisation est la première étape dans la résolution par la méthode des éléments finis. De son exactitude, dépendra la justesse des résultats. Au vu des approximations, des réserves doivent accompagner cette théorie dans l'analyse de ses résultats. L'étape suivant la

Mémoire de Master 14 Yamné A.K. KOUAMA

UFR/SI

modélisation est celle de la discrétisation puis résolution. Comment se comporte l'équation de Terzaghi lors de la résolution numérique par éléments finis? C'est la question à laquelle nous allons nous atteler à donner une réponse dans la prochaine partie de notre document.

Mémoire de Master 15 Yamné A.K. KOUAMA

UFR/SI

Chapitre 3 : Les difficultés de la résolution numérique par éléments finis de la consolidation unidimensionnelle de Terzaghi

3.1. - Introduction

En rappel l'équation établit par Terzaghi est :

_e2

t

u eu

c_v =

eu 2 e

(3. 1)

Dans cette équation, c, le coefficient de consolidation est supposé constant. Considération faite, nous avons une équation aux dérivées partielles du second ordre à coefficient constant. Une solution exacte de cette équation peut être déterminée par résolution analytique. La complexité de cette résolution, le besoin d'outils pratiques à la disposition des ingénieurs et le développement des outils informatiques sont tels que les résolutions numériques sont à l'ordre du jour. La résolution numérique par éléments finis est très utilisée dans les calculs de tassements à travers des logiciels comme Plaxis, CESAR-LCPC. Gardons à l'esprit que la résolution numérique donne une solution approchée de l'équation, la résolution analytique une solution exacte et voyons le comportement de l'équation de Terzaghi dans la résolution par éléments finis. Pour cela après avoir fait la discrétisation en espace et en temps nous ferons la résolution de l'équation dans un premier temps. Ensuite nous analyserons les résultats de la résolution aux points singuliers. Enfin nous comparerons les résultats issus de cette résolution avec la solution exacte de l'équation.

3.2. - Discrétisation en espace de la consolidation unidimensionnelle et fonction d'interpolation

Le principe de la méthode des éléments finis c'est de diviser un ensemble en plusieurs éléments afin de mieux appréhender son comportement. Considérons un massif de sol de profondeur H et perméable à ses deux limites. Nous allons le discrétiser comme suit sur la figure 3.1 : le massif est divisé en n éléments. Chaque élément, verticale, comporte deux noeuds. Les éléments peuvent avoir des longueurs différentes. Pour simplifier nous les affecterons tous de la longueur h. ( h --* 0)

Mémoire de Master 16 Yamné A.K. KOUAMA

UFR/SI

Surcharge

H

Limite perméable

h

Limite perméable

Noeud

Noeud i Elément i Noeud i+1

Fig. 3. 1. -Discrétisation en espace d'une couche de sol

Pour tout calcul avec les éléments finis, la précision est d'autant plus grande que le maillage est important.

Le maillage terminé, nous devons trouver une relation qui permet d'avoir la longueur à chaque point des éléments. Pour ce faire on utilise des fonctions d'interpolation encore appelées fonctions de forme. Il existe plusieurs types de fonctions d'interpolations, linéaires ou polynomiales. En ce qui nous concerne, consolidation unidimensionnelle, une fonction linéaire est ce qui sied. Soit:

Ni(x _j) = axj?b la fonction de forme (3. 2)

Ni (_x j) = ? ij (1 si i=j sinon 0) la fonction de Kronecker (3. 3)

N 1 ( x 1) 1

= z

= ? ? N 1' 1

N N x j

1 1 ( ) 1

? ?

h

?

?

?

?

h

(3. 4)

( x

2) = 0

N 1

N 2 ( x 1) 1

= z

= ? ? N '2 1

N N x j

2 2 ( ) 1

? ?

h

?

?

?

?

h

(3. 5)

(

x

N 2

2) = 0

3.3. - Discrétisation en temps

Soit [0, T] le temps de la consolidation. Nous allons le subdiviser en I sous-intervalles ? t i ; t i ? 1l avec i un nombre entier positif tel que:

0 ? t 0 ? ... ? ti ? ... ? t I avec dt ? ti ? ti ? 1

Désignons par u la surpression interstitielle au temps t = j et utilisons le schéma implicite en temps d'Euler, on a :

Mémoire de Master 17 Yamné A.K. KOUAMA

UFR/SI

dt

? u ui?ui?1

?

?t

(3. 6)

3.4. - Résolution numérique

La consolidation de Terzaghi et ses différentes conditions se résument comme suit :

sur ???0,H???0,T? (3. 1)

u ?u

c_v ?

? u 2 ?

_?2

t

Conditions aux limites:

u(0,t )?0

^??u

? Conditions de Dirichlet

?

(H,t)?0

Condition initiale:

? u(z,0) ? ?Q; ?Q étant la contrainte appliquée sur le massif de sol

Formulation variationelle

Soit v une fonction test appartenant à V(?) , la formulation variationelle s'écrit:

?u

?t

?
d?

2_u

(3. 7)

? c_v

d? ?u

2

? vd?

? vd?

?

dt c_v ui vd

? ? ? ?? ? ? ? ? ? ? ? ?

ui vd ? ui vd

1 (3. 8)

d? d?

d?

? '?

dt?c_v ? (_ui?v)d?? ?ui ?_vd? ? ? ? ?

?ui vd ?? ?ui?1?vd? (3. 9)

? ?d? d? ? ? d? d?

'

Or ui v d ? ' ? 0
H

?'? ? ? ui v
( ) ? ?
0

d?

car v la fonction test a les mêmes conditions aux limites que la

fonction u. Alors on a:

'

dt?c_v ? ui ^?vd?? ?ui^'?v'd?? ?ui? ?vd?

1 (3. 10)

d? d?

d?

Mémoire de Master 18 Yamné A.K. KOUAMA

UFR/SI

Détermination des matrices de rigidité et de masse élémentaires

Soit K la matrice de rigidité ou encore la conductivité du fluide et M la matrice de masse, notre équation se pose également en ces termes:

dt c_v ? K ?? ui ? ? M ?? ui ? ? M ?? ui ?

? ? ? ? 1 (3. 11)

Par ailleurs on exprime les fonctions u et v comme des combinaisons linéaires des fonctions de formes c'est-à-dire:

?

?

?

u u N u N

? 1 1 2 2

?

v v N v N

? 1 1 2 2

?

(3. 12)

Ainsi nous aurons:

K	h ? 1' 1 ' '1 ? ? N ? N N N '2 ? ? ? ? ? N N N N '2 ? '1 '2 ? '2 0 ? ?		(3. 13)
M		h ? N N N N 1 1 1 2 ? ? ? ? 0 2 1 2 2 ?? ? ?? N N N ? N		(3. 14)

En appliquant les résultats des fonctions des formes que nous avons déterminées pour un élément, il vient:

1 1 1

? ? ? ?

K ? (3. 15)
h ?? ? 1 ? 1 ??

h?2 1?

M ? (3. 16)
6 ?? 1 2 ??

L'assemblage des matrices en tenant compte des conditions aux limites donne :

Mémoire de Master 19 Yamné A.K. KOUAMA

UFR/SI

? ?

?

?

?

1 ?

K ?h ?

?

?

?

?

? ?

. .

?1 ?2 ?1

. .

2

0 ?1

. .

. .

?

.

. .

. .

.

.

.

. .

. .

. .

.

. .

. .

. .

?

. .

. .

. .

?

?

0 ?

?

?

?

?

?

?

?

?

??

0

?2 ?1 0 . . . .

0 0 0 0

(3. 17)

0 0 0 0 0 0 ? 1 ?2

2 ?1

? ?

?

?

?

h ?

M ?6 ?

?

?

?

?

? ?

41 0

01 4

00 0 0 0 0 1 4

14 1

. . .

. . .

. . .

. .

. .

. .

. .

. .

. .

. .

. .

. .

. .

. .

. .

. .

. .

. .

4 1

?

?

0 ?

?

?

?

?

?

?

?

?

??

0

0

0

0

0

(3. 18)

On aboutit finalement à un système linéaire:

( ? ? ? ? ) ? ? ? ?? 1 ? ? 0?

dt ? c_v K ? M ui ? M ui ? ? (3. 19)

Pour la résolution de ce système linéaire, le premier pas de temps doit faire intervenir la condition initiale. Il s'agira donc de déterminer u1 dans ce système car _{u1_1est} connu dans l'opération antérieure.

3.5. - Résolution numérique adimensionnelle

Pour cela nous allons introduire deux paramètres dans notre équation :

-l'épaisseur adimensionnelle Z :

z

Z ? (3. 20)

H d

Hd est la hauteur drainante. Elle correspond à la distance maximale que doit parcourir le fluide pour atteindre une zone de drainage. Dans le cadre de la théorie de la consolidation, elle est égale à la demi-hauteur.

Mémoire de Master 20 Yamné A.K. KOUAMA

UFR/SI

Dans cette partie on prend 0 ? z ? H , on résout l'équation pour cette partie et on opère par 2

symétrie pour H ? z ? H

2

-Le facteur de temps T :

CV t ? TV ? H d 2 On établit l'équation adimensionnelle suivante:

(3. 21)

( , )

Z _{T v}?u( Z ,

? z

u ( Z ,0) ? ? Q

?u T v (0, )

T v ) ?

?

?

?

? ? ? ?

2 ?T v

0

(3. 22)

?

2 u

0

? u T v

(1, )

Cette équation nous donne l'évolution de la surpression interstitielle en fonction du facteur temps et de l'épaisseur adimensionnelle. Les résultats que nous établirons sont ceux de la consolidation unidimensionnelle de Terzaghi pour toutes les épaisseurs de sols. L'équation sera résolue une fois pour toutes. La résolution est identique à celle établie dans la partie 3.4. On aura donc:

( ? ? ? ? ) ? ( , ) ? ? ?? 1 ( , ) ? ? 0?

d _Tv K M u i Z _Tv ^M _ui ^Z T_v

? ? ? ? ? (3. 23)

Les matrices [K]et [M] sont celles déterminées plus haut. La résolution sur Matlab de cette équation nous donne la figure 3.2:

Mémoire de Master 21 Yamné A.K. KOUAMA

UFR/SI

Fig. 3. 2:Solution de la consolidation unidimensionnelle de Terzaghi par éléments finis

3.6. - Analyse de la résolution pour les éléments situés aux limites perméables

En rappel la résolution par éléments finis est une méthode qui donne une solution approchée. Son exactitude sera donc fonction de sa concordance avec la solution exacte qui est analytique. Mais avant, nous pouvons faire une analyse de la démarche de cette méthode par rapport au problème physique avec ses contraintes aux niveaux des points particuliers.

Les éléments finis à travers les fonctions de forme procèdent par interpolation pour la détermination de la surpression dans chaque élément. Cette démarche se justifie par le fait que dans un élément infiniment petit, deux valeurs infiniment proches peuvent être liées par une relation d'interpolation.

Les conditions initiales de la consolidation unidimensionnelle donnent:

)

?

u

0

(0,0

u (H,

(3. 24)

0) ? 0

)

?

0

A

?

??

??

u(z,

Q

La surpression interstitielle est égale à la surcharge en tout point du sol sauf aux limites perméables. Pour les deux éléments du maillage dont un noeud est au niveau de la limite perméable, on a pour t = 0:

Mémoire de Master 22 Yamné A.K. KOUAMA

UFR/SI

ru

? ? u Q

2 = A

Mémoire de Master 23 Yamné A.K. KOUAMA

UFR/SI

1 0

=

-* u(z) = AQx N2 : Cette fonction est une droite (3. 25)

La fonction u(z) est une droite croissante pour la méthode des éléments finis au lieu d'être une droite constante de valeur Lq sur tout l'élément sauf au noeud 1. La représentation graphique de cet état de fait est la suivante:

Fig. 3. 3. -Représentation de la consolidation initiale dans un élément à la limite perméable

Nous voyons clairement que les éléments finis sont incapables de prendre en compte cette singularité. Une interpolation ne peut pas définir correctement la condition initiale de la consolidation unidimensionnelle.

On peut donc projeter que pour des petits pas de temps c'est-à-dire pour des temps ou u(z) Lq des erreurs apparaitront dans le calcul des surpressions interstitielles par la méthode des éléments finis dans la zone des limites perméables. Ce temps est une fonction des conditions de drainage et du type de sol. Avec la discrétisation en temps ces erreurs vont diminuant.

Fig. 3. 4. -Evolution de l'erreur dans les premiers instants

Au cours de la consolidation la surpression diminue d'abord aux abords des limites perméables pour ensuite s'étendre aux éléments plus loin. Donc au temps où on commence à avoir une surpression interstitielle nulle ou presque nulle dans les éléments proches de la limite perméable, la singularité au niveau de la limite perméable pour les instants initiaux disparait. En ce moment le principe de la méthode des éléments finis se superpose au phénomène physique réel. Cette superposition est le fruit de la discrétisation en temps.

Fig. 3. 5. -Evolution jusqu'à dissipation de l'erreur

En effet la discrétisation en temps permet de réduire au fur et à mesure la singularité de la condition initiale. Avec l'incrémentation, chaque valeur trouvée avec un incrément dt devient la valeur de _{14_1} pour le calcul de l'incrément suivant. La condition initiale est donc utilisée pour le premier incrément et s'efface ensuite lors du calcul, c'est la raison pour laquelle les éléments finis finissent par se superposer au phénomène physique.

3.7. - Analyse de la résolution au niveau de l'assemblage des éléments.

Dans le chapitre 2, nous parlions des hypothèses approximatives de Terzaghi. Dans sa théorie

k yw

et mv sont constants. Il les couple pour donner

k cv = , une constante. mv yw x

Découplons le coefficient de consolidation c de l'équation classique de Terzaghi pour voir son comportement dans la résolution par élément finis.

ô2 u ô u

t

cv ôu2 -->Equation classique ? dtx c_v[K}[ui}+[M}[ui}=[MXui-1} (3. 26)

Mémoire de Master 24 Yamné A.K. KOUAMA

UFR/SI

2u ?u ? Équation découplée - dt? k ?K??ui}+mv~M??ui??mv?M??ui?1?

y_w

k ?

?

m_v

t

2

?

?u

y_w

(3. 27)

Soit:

?Kk? ? c_v?K? ou ? ? ? K?

k

Kk ? (3. 28)

y_w

et ?M_m? ? ? M? ou?M_m? ? m_v?M? (3. 29)

Considérons un massif de sol avec deux sous couches dont les caractéristiques sont les suivantes: Tableau 3. 1.-Paramètres de deux couches différentes d'un sol

c

ki h m

~~

Couche 1	1	1	1	1
Couche 2	10	1	10	1

La résolution pour l'équation classique de Terzaghi donne:

?? 1 ? 1 ?

? ? ? ?

Kk ₁ Kk 2

? ? (3. 30)
?? ? 1 ?1??

?M _m?₁??M m?2 6??1 2 1 ?2 ? (3. 31)
J

L'assemblage donne:

(3. 32)

(3. 33)

? 1

K k ? ? ?1 ? ? ? ? ? 0 ?2 1 ? 1 M m ? ? ? 6 ? ? ? 0

?1 2 ?1 1 4 1

0? ?1 ? ? 1 ?? 0? 1 ? ? 2??

La résolution pour l'équation découplée donne:

?? 1 ?1?

? ?

Kk ? (3. 34)
1 ?? ? 1 ? 1??

Mémoire de Master 25 Yamné A.K. KOUAMA

UFR/SI

??10 ?10?

? ?

K k ? (3. 35)
2 ?? ? 10 ? 10 ??

1 ? 2 1 ?

? ?

M m ? (3. 36)

1 6 ??1 2 ??

1?20 10?

? ?

M m ? 10 20 (3. 37)

2 6 ?? ??

L'assemblage aboutit à :

? ? K k	? 1 ?1 0? ? ? ? 1 11 10 (3. 38) ? ? ? ? ? ? 0 ?10 10??
? ? M m		? 2 1 0? 1 ? 1 22 10 ? ? (3. 39) 6 ? ? ? ? 0 10 20??

Clairement on voit que nous n'aboutissons pas aux mêmes matrices. Ce qui implique que la surpression interstitielle qui sera déterminée ne sera pas pareille quand bien même nous avons le même coefficient de consolidation c, = 1. La conclusion qui découle de cette partie c'est que la consolidation de Terzaghi par éléments finis n'est pas appropriée pour le calcul dans les sols multicouches.

3.8. - Solution exacte de l'équation et solution par éléments finis

La solution exacte de la consolidation unidimensionnelle est obtenue par la résolution analytique. La solution par la loi de Fourier donne :

2

2

u z t u z t

e ? ?

( , ) ? ( ,0) c_v )

( (3. 40)
z

La résolution numérique donne une solution approchée de l'équation. Avec l'analyse sur les erreurs qui pouvaient survenir il est important de voir comment cette résolution se comporte vis-à-vis de celle exacte. La recherche bibliographique (fig3.6) nous donne les évolutions à différents temps de la surpression interstitielle.

Mémoire de Master 26 Yamné A.K. KOUAMA

UFR/SI

Fig. 3. 6 : Comparaison de l'évolution de la surpression interstitielle dans un calcul par

éléments finis (FEM) et la solution exacte de l'équation (Terzaghi) (MOHAMAD et al, 2012)

Il apparait que les deux solutions ont la même allure et se superposent quasiment. En plus la

représentation du degré de consolidation en fonction du facteur temps (fig3.7) nous conforte dans nos propos vue la bonne superposition qu'elle représente.

Mémoire de Master 27 Yamné A.K. KOUAMA

UFR/SI

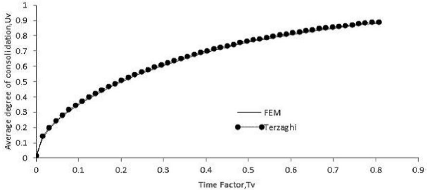
Fig. 3. 7 : Comparaison de l'évolution du degré de consolidation moyenne (MOHAMAD et

al, 2012)

Maintenant si nous prenons le cas du calcul pour les sols multicouches, nous voyons que la figure 3.8 nous donne des courbes différentes.

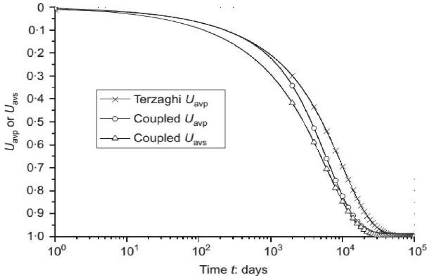
Fig. 3. 8 : Comparaison de l'évolution du degré de consolidation moyenne pour les sols
multicouches (HUANG et al, 2010)

3.9. - Conclusion

Les erreurs dans la résolution numérique par éléments finis résident dans les conditions initiales de la consolidation portant sur les surpressions. L'ampleur de ces erreurs dépend de la

Mémoire de Master 28 Yamné A.K. KOUAMA

UFR/SI

grossièreté du maillage des éléments et du pas d'incrémentation en temps. Les éléments situés dans les limites perméables présenteront des oscillations qui s'estompent dans le temps. On déduit qu'il est préférable de ne pas employer de pas de temps trop faibles pour le début des calculs de consolidation, ce qui ne présente d'ailleurs aucun inconvénient pour les applications pratiques puis que les changements ne sont jamais instantanés et que la journée est l'unité de temps minimale pour les études de consolidation dans la nature. En plus l'étude comparée de la résolution numérique par éléments finis et celle analytique nous montre une concordance des résultats. Néanmoins il y'a un problème dans le calcul de consolidation dans les sols multicouches. A ce niveau le calcul peut conduire à des erreurs si on ne décompose pas le coefficient de consolidation.

Mémoire de Master 29 Yamné A.K. KOUAMA

UFR/SI

Conclusion générale et perspectives

La consolidation est la diminution du volume d'un sol due au drainage de l'eau qu'il contient dans ses pores. Dans les sols fins le tassement principal est celui de consolidation. Pouvoir prédire avec exactitude cette consolidation c'est avoir les moyens pour faire face au tassement des ouvrages et assurer leur stabilité. Avec le développement informatique des méthodes de résolution numérique comme celle de la méthode des éléments finis sont d'actualité. Pour résoudre un problème physique avec cette méthode on passe par trois phases à savoir la modélisation, la discrétisation et la résolution numérique.

En 1923, Karl Terzaghi modélise la consolidation unidimensionnelle. Avec de nombreuses hypothèses, en combinant les équations de conservations de masse, de compressibilité du squelette, d'écoulement hydraulique de Darcy il établit une équation aux dérivées partielles du second ordre à coefficient constant. Cette équation de couplage hydromécanique est fortement sujette à caution. Les hypothèses émises par Terzaghi sont parfois des approximations de la réalité du phénomène physique. Elles présentent des limites si bien qu'elles ne peuvent pas reproduire fidèlement l'état de tous les sols fins. Au fil des années d'autres théories sont nées pour rectifier ces hypothèses. En témoigne celle de la consolidation bidimensionnelle ou tridimensionnelle par exemple. La multiplicité des sols et la difficulté de couplage sont telles qu'il est difficile de trouver une théorie adéquate qu'on puisse appliquer de façon systématique aux sols.

On note quand même que la théorie de la consolidation de Terzaghi est toujours la référence dans le calcul de consolidation. A l'instant initial de la consolidation, la pression interstitielle est nulle aux limites perméables et égale à la surcharge appliquée dans le reste de l'élément de sol. Les éléments finis sont incapables de modéliser cette singularité. Des erreurs apparaissent dès lors dans les résultats aux premiers instants de la consolidation. Ces erreurs s'estompent dans le temps et les résultats finissent par se superposer aux résultats du calcul analytique. La résolution par éléments finis est donc satisfaisante pour ce problème sauf dans le cas de sols à couches distinctes. Dans ce cas de figure il convient de ne pas utiliser le coefficient de consolidation c, mais plutôt de le décomposer.

La consolidation est un phénomène complexe. On sait qu'en plus du couplage hydromécanique un paramètre comme la température influe également sur la consolidation. Une suite de ce travail pourrait être une réflexion sur le couplage thermo hydromécanique de la consolidation.

Mémoire de Master 30 Yamné A.K. KOUAMA

UFR/SI

Références bibliographiques

ARABET, L. (2010). - Modélisation numérique du tassement et de la consolidation des sols sous l'oedomètre ; mémoire de magister en génie civil, Université 20 Août 1955 de Skikda

BASSEVILLE, S. et FEYEL, F. (2006). - Méthodes de résolution en éléments ; Note de cours. BERTHAUD, Y. DE BUHAN, P. SCHMITT, N. (2008). -Notes de cours : Mécanique des sols.

BOURGES, F. et MIEUSSENS, C. (1979). - Déplacements latéraux à proximité des remblais sur sols compressibles : Méthode de prévision ; Bull, liaison Labo. Ponts et Chaussées.

DAVIS, F. and POULOS, H. (1968). - The use of elastic theory of settlement prediction under three dimensional conditions; Géotechnique, vol. XVIII.

DI FRANCESCO, R. (2008). - Exact solution to Terzaghi's consolidation equation; GEO&GEO Instruments® - research & development Teramo (TE), Italy.

FÉLIX, B. et BOUTAYEB, N. (1981). - Compressibilité à court terme et saturation imparfaite des sols argileux ; bulletin de liaison Laboratoire Ponts et Chaussées.115 -sept.-Réf.2605

GARDNER,W.R. (1974).-The Permeability Problem"; Soil Science, Vol. 117, No. 5.

GRARI, M. et KORIKACHE, N.(2007) - Implémentation des éléments finis sous Matlab ; Exposé en EDP.

HANSBO, S. (1960). - Consolidation of clay with special reference to influence of vertical sans drains; Swedish Geotechnical institute Proc, No. 18.

HUANG, J. and GRIFFITHS ,D. (2010). - One-dimensional consolidation theories for layered soil and coupled and uncoupled solutions by the finite-element method; Géotechnique 60, No. 9, 709-713.

IZBASH, S.V. (1931). - Filtratsi v kroupnozernistom materiale (Filtration dans les matériaux grossiers) ; Leningrad: Inst. Gidrotechniki (NIIG).

LI , Xiang-Ling. (1999). - Comportement Hydromécanique des Sols Fins : de l'état saturé à l'état non saturé ; thèse de Doctorat, Sciences appliquées de l'Université de Liège.

LUTZ, J.F. AND KEMPER, W.D. (1959). - Intrinsic permeability of clay as affected by claywater interaction; Soil Science, 1959, Vol. 88.

MAGNAN, J-P. (1988). - Déformabilité des sols. Tassements. Consolidation ; Techniques de l'Ingénieur, traité Construction.

MIEUSSENS, C. et DUCASSE, P. (1980).- Etude numérique de la consolidation bidimensionnelle: Le programme BIDIF ; Bull, liaison Labo. Ponts et Chaussées.

Mémoire de Master 31 Yamné A.K. KOUAMA

UFR/SI

MILLER R. J and LOW P. F. (1963). - Threshold gradient for water in clay system; Proc. of the soil Science Society of America, Vol. 27, N° 6.

MITCHELL, J.K. and YOUNGER, J.S. (1967). - Abnormalities in hydraulic flow through finegrained soils, Permeability and Capillarity of Soils; ASTM STP 417.

MITCHELL, J.K. (1976). - The properties of cement stabilized soils, Residential workshop on materials and methods for low cost roads, rail and reclamation work leurra, Australia.

NASRI, V. et MAGNAN, JP. (1997). - Comportement numérique des éléments finis dans l'analyse des problèmes de consolidation des sols ; bulletin des laboratoires des ponts et chaussées -210- Juillet-Aout 1997-RÉF.414 2-PP.41-53

ROUSSELOT, D. (1975). - Simulation des tassements de sols selon la théorie de la consolidation unidimensionnelle de Terzaghi ; Informatique hydro géotechnique, BRGM

WAN HASSAN, W. and MOHAMAD, H. (2012). - Evaluation of finite element formulation for one-dimensional consolidation; International Journal of Scientific & Engineering Research, Volume 3, Issue 5.

ZOU, Y. (1996). -A non-linear permeability relation depending on the activation energy of pore liquid ; Géotechnique, Vol. 46, No. 4.

Mémoire de Master 32 Yamné A.K. KOUAMA

UFR/SI

Table des matières

Avant-propos i

Liste des notations et des abréviations iv

Résumé vi

Introduction générale 1

Chapitre 1.- Revue bibliographique : La consolidation, un comportement hydromécanique 2

1.1. - Introduction 2

1.2. - Le tassement 2

1.3. - Phénomène de consolidation 3

1.4. - Théorie de la consolidation unidimensionnelle de Terzaghi 4

1.5. - La méthode des éléments finis et ses sources d'erreurs 5

1.6. - Conclusion 6

Chapitre 2 : Les limites de la modélisation de la consolidation unidimensionnelle de Terzaghi

7

2.1. - Introduction 7

2.2. - Modélisation de la consolidation unidimensionnelle de Terzaghi 7

2.3. - La validité de la loi de Darcy 10

2.4. - La constance de la perméabilité 11

2.5. - La compressibilité du fluide (eau + gaz) 12

2.6. - L'homogénéité des sols 12

2.7. - La relation linéaire entre l'indice des vides et la contrainte effective 12

2.8. - La consolidation unidimensionnelle 13

2.9. - L'importance de la compression secondaire 14

2.10. - Conclusion 14

Chapitre 3 : Les difficultés de la résolution numérique par éléments finis de la consolidation

unidimensionnelle de Terzaghi 16

3.1. - Introduction 16

3.2. - Discrétisation en espace de la consolidation unidimensionnelle et fonction

d'interpolation 16

3.3. - Discrétisation en temps 17

3.4. - Résolution numérique 18

Mémoire de Master 33 Yamné A.K. KOUAMA

UFR/SI

3.5. - Résolution numérique adimensionnelle 20

3.6. - Analyse de la résolution pour les éléments situés aux limites perméables 22

3.7. - Analyse de la résolution au niveau de l'assemblage des éléments. 24

3.8. - Solution exacte de l'équation et solution par éléments finis 26

3.9. - Conclusion 28

Conclusion générale et perspectives 30

Références bibliographiques 31

Table des matières 33

Listes des figures et tableaux 35

Annexes 36

Mémoire de Master 34 Yamné A.K. KOUAMA

UFR/SI

Listes des figures et tableaux

Fig. 1.1.- Modèle rhéologique de la consolidation (Magnan, 1988) 3

Fig. 1. 2.- Définition des couches de sols et du chargement (Terzaghi, 1923) 4

Fig. 2. 1- Gradient seuil apparent et déviation de linéarité (Miller et Low, 1963) 11

Fig. 2. 2.- Allures des courbes de compressibilités (Magnan,1988) 13

Fig. 2. 3.- Comparaison des temps de consolidation en fonction des considérations sur le sens

de l'écoulement de l'eau (MIEUSSENS et al, 1980) 14

Fig. 3. 1. -Discrétisation en espace d'une couche de sol 17

Fig. 3. 2:Solution de la consolidation unidimensionnelle de Terzaghi par éléments finis 22

Fig. 3. 3. -Représentation de la consolidation initiale dans un élément à la limite perméable 23

Fig. 3. 4. -Evolution de l'erreur dans les premiers instants 23

Fig. 3. 5. -Evolution jusqu'à dissipation de l'erreur 24

Fig. 3. 6 : Comparaison de l'évolution de la surpression interstitielle dans un calcul par éléments finis (FEM) et la solution exacte de l'équation (Terzaghi) (MOHAMAD et al,

2012) 27
Fig. 3. 7 : Comparaison de l'évolution du degré de consolidation moyenne (MOHAMAD et

al, 2012) 28
Fig. 3. 8 : Comparaison de l'évolution du degré de consolidation moyenne pour les sols

multicouches (HUANG et al, 2010) 28

Tableau 1.1- Evolution des contraintes au cours de la consolidation (Magnan, 1988) 4

Tableau 3. 1.-Paramètres de deux couches différentes d'un sol 25

Mémoire de Master 35 Yamné A.K. KOUAMA

UFR/SI

Mémoire de Master 36 Yamné A.K. KOUAMA

UFR/SI

Annexes

Ecriture du programme de calcul de la consolidation unidimensionnelle de Terzaghi dans Matlab :

global R invM

N =20;

h =1/(N+1) ;

z=(0: h :1)';

M=h/6*(4*diag(ones(N,1))+ diag(ones(N-1,1),1)+diag(ones(N-1,1),-1));

invM=inv(M);

R=1/h*(2*diag(ones(N,1))-diag(ones(N-1,1),1)-diag(ones(N-1,1),-1));

eta0=u0(z(2:N+1));

[t,V]=ode23('surpres',[0,1],eta0);

V=[zeros(length(t),1),V, zeros(length(t),1)];

[ZZ,TT]=meshgrid(z,t);

mesh(ZZ,TT,V)

surf (ZZ,TT,V,'EdgeColor','none')

xlabel('Z','Fontsize',12)

ylabel ('Tv','Fontsize',12)

zlabel ('u(Z,Tv)/u0(Z)','Fontsize',12)