1.3. Modèles Vectoriel Auto
Régressif (VAR)
Il s'agit d'un modèle qui ne s'intéresse qu'aux
relations statistiques qui existent entre les variables. La modélisation
VAR permet en effet d'exprimer chaque indicateur ou agrégat
endogène comme fonction linéaire des valeurs passées
(retardées) de tous les indicateurs endogènes et valeurs
présentes ou retardées des exogènes. Ce modèle
offre des facilités de calcul et des possibilités de
prévisions. Il est bien utilisable dans le cadre de l'analyse des
impacts de la production agricole sur la croissance économique au
Bénin à cause de sa simplicité, ses facilités et
des applications qu'il permet de réaliser.
A- Présentation du Modèle VAR
Considérons un vecteur 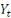 constitué d'indicateurs ou d'agrégats
macroéconomiques supposés endogènes et un vecteur constitué d'indicateurs ou d'agrégats
macroéconomiques supposés endogènes et un vecteur 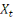 constitué de variables de politique économique
(exogènes) et un vecteur constitué de variables de politique économique
(exogènes) et un vecteur  des innovations du processus. des innovations du processus.
Soient :
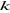 le nombre de variables endogènes ; le nombre de variables endogènes ;
 le nombre de variables exogènes ; le nombre de variables exogènes ;
 , i=1;......; p des matrices , i=1;......; p des matrices 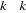 coefficients des coefficients des 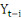 dans la régression ; dans la régression ;
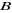 une matrice une matrice  coefficient de coefficient de  dans la régression ; dans la régression ;
 le nombre de retard dans la régression ; le nombre de retard dans la régression ;
Alors le modèle s'écrit :

Dans ce système, les composantes du vecteur  peuvent être corrélées entre elles pour un instant
t donné mais elles ne sont ni corrélées avec leurs valeurs
passées ni avec les membres de droites de l'équation. Comme ce ne
sont que les valeurs retardées des variables endogènes qui
apparaissent du côté droit de chaque équation, Il n'y a pas
de problèmes de spontanéité et les MCO sont simplement
applicables. Ainsi, le modèle VAR présente l'avantage
d'être facilement estimable tout en prenant en compte les relations entre
les valeurs présentes des variables et leurs valeurs retardées.
Il permet aussi : peuvent être corrélées entre elles pour un instant
t donné mais elles ne sont ni corrélées avec leurs valeurs
passées ni avec les membres de droites de l'équation. Comme ce ne
sont que les valeurs retardées des variables endogènes qui
apparaissent du côté droit de chaque équation, Il n'y a pas
de problèmes de spontanéité et les MCO sont simplement
applicables. Ainsi, le modèle VAR présente l'avantage
d'être facilement estimable tout en prenant en compte les relations entre
les valeurs présentes des variables et leurs valeurs retardées.
Il permet aussi :
· de faire des chocs (impulsions) afin d'évaluer
les impacts de la variabilité d'une variable endogène sur les
autres endogènes ;
· d'opérer une décomposition de la variance
pour mieux cerner l'importance relative de chaque innovation aléatoire
des variables du VAR ;
· de procéder aux tests de causalité
à la Granger (1969) qui aident à estimer la part d'explication
que les valeurs passées ou retardées d'un vecteur apportent
à un autre vecteur ;
· d'effectuer des prévisions ;
· d'étudier la cointégration des variables
macroéconomiques pour appréhender les relations de long terme.
Ce modèle peut prendre en compte :
· des restrictions dues à des identités
comptables et aux structures de certains domaines de l'économie (il
s'agit dans ce cas de VAR structurels) ;
· de vérifier si à un moment donné
une structure a changé, puis d'en évaluer
les conséquences éventuelles (VAR avec rupture
structurelle à un point inconnu) ;
| 


