Conclusion : M1_SCR est I(1)
Etude de la série LNM1SCR

13.0
12.8
12.6
12.4
12.2
12.0
11.8
02 03 04 05 06 07 08 09 10 11
LNM1_SCR
Ce graphe fait apparaître une tendance évidente.
Nous allons donc procéder aux tests ADF pour déterminer sa
nature.
46
Estimation du modèle [3] pour LNM1_SCR :

La statistique t relative à Ö étant
supérieure à sa valeur critique, on accepte H0 et on passe au
test de l'hypothèse H0,3 :
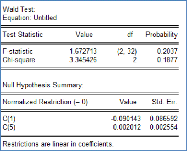
La p-value relative à la statistique F étant
supérieure à 5%, on accepte H0,3 et on passe à
l'estimation du modèle [2].
47
Estimation du modèle [2] pour LNM1_SCR :

La statistique t relative à Ö étant
supérieure à sa valeur critique, on accepte H0 et on passe au
test de l'hypothèse H0,2 :

La p-value relative à la statistique F étant
inférieure à 5%, on rejette H0,2, on conclut que
LNM1_SCR est I(1) + C. La meilleure façon de la stationnariser est de la
différencier.
Le graphe de cette nouvelle série se présente comme
suit :

-.02
-.04
.10
.08
.06
.04
.02
.00
02 03 04 05 06 07 08 09 10 11
LNM1_SCRD1
48
Estimation du modèle [3] pour LNM1_SCRD1
:

La statistique t relative à Ö étant
supérieure à sa valeur critique, on accepte H0 et on passe au
test de l'hypothèse H0,3 :

La p-value relative à la statistique F étant
inférieure à 5%, on rejette H0,3 et on conclut que
LNM1_SCRD1 est I(1) + C + â.t. Pour la stationnariser il faut la
différencier puis retirer la tendance. Cela revient à prendre le
résidu de la régression suivante :
LNM1_SCRD1t - LNM1_SCRD1t-1 = C +
â.t + åt
Le résultat de cette régression est comme suit :

Le graphe du résidu issu de cette régression se
présente comme suit :

-.04
-.08
-.12
.08
.04
.00
02 03 04 05 06 07 08 09 10 11
LNM1_SCRD1RES
49
50
Les tests ADF réalisés sur cette série
montent qu'elle est stationnaire. Conclusion : LNM1_SCR est
I(2)
Etude de la série M3- M1 :
Pour rappel ce sous-agrégat contient les comptes
d'épargne auprès des banques et les comptes sur livrets
auprès de la caisse d'épargne nationale ainsi que les comptes
à terme et bons de caisse auprès des banques.
Le graphe de la série M3_M1 se présente comme suit
:
M3_M1
|
400,000 350,000 300,000 250,000 200,000 150,000 100,000
|
|
2002 2003 2004 2005 2006 2007 2008 2009 2010 2011
Nous allons procéder aux tests ADF pour déterminer
la nature de cette série. Estimation du modèle [3] pour M3_M1
:
51
|
Null Hypothesis: M3_M1 has a unit root Exogenous: Constant,
Linear Trend
Lag Length: 1 (Automatic - based on SIC, maxlag=9)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic -2.027535
|
0.5680
|
|
Test critical values: 1% level -4.219126
|
|
|
5% level -3.533083
|
|
|
10% level -3.198312
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(M3_M1)
|
|
|
Method: Least Squares
|
|
|
Date: 06/11/13 Time: 12:41
|
|
|
Sample (adjusted): 2002Q3 2011Q4
|
|
|
Included observations: 38 after adjustments
|
|
|
Variable Coefficient Std. Error t-Statistic
|
Prob.
|
|
M3_M1(-1) -0.119044 0.058714 -2.027535
|
0.0505
|
|
D(M3_M1(-1)) 0.279879 0.157088 1.781668
|
0.0837
|
|
C 13065.24 5402.700 2.418279
|
0.0211
|
|
@TREND("2002Q1") 951.8607 441.6675 2.155152
|
0.0383
|
|
R-squared 0.194343 Mean dependent var
|
6298.051
|
|
Adjusted R-squared 0.123256 S.D. dependent var
|
6843.559
|
|
S.E. of regression 6407.940 Akaike info criterion
|
20.46776
|
|
Sum squared resid 1.40E+09 Schwarz criterion
|
20.64014
|
|
Log likelihood -384.8875 Hannan-Quinn criter.
|
20.52909
|
|
F-statistic 2.733869 Durbin-Watson stat
|
2.004488
|
|
Prob(F-statistic) 0.058801
|
|
La statistique t relative à Ö étant
supérieure à sa valeur critique, on accepte H0 et on passe au
test de H0,3
|
Wald Test: Equation: Untitled
|
|
|
|
Test Statistic Value
|
df
|
Probability
|
|
F-statistic 2.383466
Chi-square 4.766931
|
(2, 34)
2
|
0.1075
0.0922
|
|
Null Hypothesis: C(1)=0,C(4)=0 Null Hypothesis Summary:
|
|
|
|
Normalized Restriction (= 0)
|
Value
|
Std. Err.
|
|
C(1) C(4)
|
-0.119044
951.8607
|
0.058714
441.6675
|
|
Restrictions are linear in coefficients.
|
|
La p-value relative à la statistique F étant
supérieure à 5%, on accepte H0,3 et on passe donc
à l'estimation du modèle [2].
Estimation du modèle [2] pour M3_M1 :
52
|
Null Hypothesis: M3_M1 has a unit root
Exogenous: Constant
Lag Length: 0 (Automatic - based on SIC, maxlag=9)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic 0.811014
|
0.9930
|
|
Test critical values: 1% level -3.610453
5% level -2.938987
10% level -2.607932
|
|
|
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation Dependent Variable:
D(M3_M1) Method: Least Squares
Date: 06/11/13 Time: 13:10
Sample (adjusted): 2002Q2 2011Q4 Included observations: 39 after
adjustments
|
|
|
Variable Coefficient Std. Error t-Statistic
|
Prob.
|
|
M3_M1(-1) 0.010779 0.013291 0.811014
C 3599.584 3274.426 1.099302
|
0.4225
0.2787
|
|
R-squared 0.017466 Mean dependent var
Adjusted R-squared -0.009089 S.D. dependent var
S.E. of regression 6896.838 Akaike info criterion
Sum squared resid 1.76E+09 Schwarz criterion
Log likelihood -399.0260 Hannan-Quinn criter.
F-statistic 0.657743 Durbin-Watson stat
Prob(F-statistic) 0.422544
|
6099.587 6865.709 20.56543 20.65074 20.59604 1.416664
|
|
|
La statistique t relative à Ö étant
supérieure à sa valeur critique, on accepte H0 et on passe au
test de H0,2 :
|
Wald Test: Equation: Untitled
|
|
|
|
Test Statistic Value
|
df
|
Probability
|
|
F-statistic 15.58117
Chi-square 31.16235
|
(2, 37)
2
|
0.0000
0.0000
|
|
Null Hypothesis: C(1)=0,C(2)=0 Null Hypothesis Summary:
|
|
|
|
Normalized Restriction (= 0)
|
Value
|
Std. Err.
|
C(1)
C(2)
|
0.010779
3599.584
|
0.013291
3274.426
|
|
Restrictions are linear in coefficients.
|
|
La p-value relative à la statistique F étant
inférieure à 5%, on rejette H0,2 et on conclut donc
que M3_M1 est DS avec Drift. La meilleure façon de la stationnariser est
de la différencier. Le graphe de cette nouvelle série se
présente comme suit :
M3_M1D1
|
25,000 20,000 15,000 10,000 5,000
0
-5,000
|
|
2002 2003 2004 2005 2006 2007 2008 2009 2010 2011
53
Nous allons procéder aux tests ADF pour voir est ce
qu'elle est stationnaire. Estimation du modèle [3] pour M3_M1D1
:
|
Null Hypothesis: M3_M1D1 has a unit root Exogenous: Constant,
Linear Trend
Lag Length: 0 (Automatic - based on SIC, maxlag=9)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic -4.478063
|
0.0052
|
|
Test critical values: 1% level -4.219126
|
|
|
5% level -3.533083
|
|
|
10% level -3.198312
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(M3_M1D1)
|
|
|
Method: Least Squares
|
|
|
Date: 06/11/13 Time: 13:16
|
|
|
Sample (adjusted): 2002Q3 2011Q4
|
|
|
Included observations: 38 after adjustments
|
|
|
Variable Coefficient Std. Error t-Statistic
|
Prob.
|
|
M3_M1D1(-1) -0.733409 0.163778 -4.478063
|
0.0001
|
|
C 3139.038 2384.404 1.316487
|
0.1966
|
|
@TREND("2002Q1") 77.79646 100.2276 0.776198
|
0.4428
|
|
R-squared 0.364285 Mean dependent var
|
430.6905
|
|
Adjusted R-squared 0.327958 S.D. dependent var
|
8156.632
|
|
S.E. of regression 6686.656 Akaike info criterion
|
20.52927
|
|
Sum squared resid 1.56E+09 Schwarz criterion
|
20.65856
|
|
Log likelihood -387.0562 Hannan-Quinn criter.
|
20.57527
|
|
F-statistic 10.02805 Durbin-Watson stat
|
1.974543
|
|
Prob(F-statistic) 0.000361
|
|
La statistique t relative à Ö étant
inférieure à sa valeur critique, on rejette H0. Cependant, la
tendance n'est pas significative au seuil de 5%, on doit tester le
modèle [2].
54
Estimation du modèle [2] pour M3_M1D1
:
|
Null Hypothesis: M3_M1D1 has a unit root Exogenous: Constant
Lag Length: 0 (Automatic - based on SIC, maxlag=9)
|
|
|
t-Statistic
|
Prob.*
|
|
Augmented Dickey-Fuller test statistic -4.435181
|
0.0011
|
|
Test critical values: 1% level -3.615588
5% level -2.941145
10% level -2.609066
|
|
|
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation Dependent Variable:
D(M3_M1D1) Method: Least Squares
Date: 06/11/13 Time: 13:18
Sample (adjusted): 2002Q3 2011Q4 Included observations: 38 after
adjustments
|
|
|
Variable Coefficient Std. Error t-Statistic
|
Prob.
|
|
M3_M1D1(-1) -0.712925 0.160743 -4.435181
C 4613.677 1432.875 3.219874
|
0.0001
0.0027
|
|
R-squared 0.353342 Mean dependent var
Adjusted R-squared 0.335379 S.D. dependent var
S.E. of regression 6649.636 Akaike info criterion
Sum squared resid 1.59E+09 Schwarz criterion
Log likelihood -387.3804 Hannan-Quinn criter.
F-statistic 19.67083 Durbin-Watson stat
Prob(F-statistic) 0.000083
|
430.6905 8156.632 20.49371 20.57990 20.52437 1.982157
|
|
|
La statistique t relative à Ö étant
inférieure à sa valeur critique, on rejette H0. La constante est
significativement différente de zéro, donc M3_M1D1 est
stationnaire autour d'une moyenne.
| 


