III.4. Principe fondamental
de la dynamique (PFD) appliqué au tiroir
Le principe fondamental de la dynamique (PFD) appliqué
au tiroir du distributeur et en déduire la forme canonique de la
fonction de transfert :
· Théorème de la résultante
dynamique :
- En projectant sur 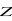
 (3.7) (3.7)
Les forces des ressorts s'expriment :
 (3.8) (3.8)
 (3.9) (3.9)
Les pressions aux extrémités du tirroir
s'expriment :
 (3.10) (3.10)
 (3.11) (3.11)
En remplaçant dans l'équation sur  : :
 (3.12) (3.12)
· Transformée de Laplace de
l'équation :
Nous considérons les conditions suivantes à
t=0
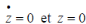 (3.13) (3.13)
Ainsi, nous pouvons écrire :
 (3.14) (3.14)
· Fonction de transfert
Divisons le numérateur et le dénominateur par
2kt.
· Fonction de transfert sous sa forme canonique :
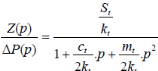 (3.15) (3.15)
D'où le schéma bloc du servovalve peut
s'écrire :
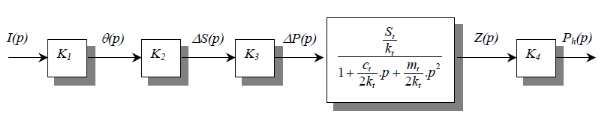
Figure 3.10 : Schéma bloc du servovalve
On admet enfin que la pression d'utilisation
Ph(t)du fluide est proportionnelle au déplacement z(t) du
tiroir :
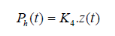 (3.16) (3.16)
III.5. Fonction de
transfert de la servovalve
La fonction de transfert de la servovalve et montrer qu'elle
peut se mettre sous la forme d'un système du second ordre :
 (3.17) (3.17)
· Fonction de transfert sous sa forme canonique :
 (3.18) (3.18)
· Coefficients caractéristiques de la fonction de
transfert du second ordre :
Gain statique :
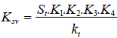 (3.19) (3.19)
Pulsation propre :
 (3.20) (3.20)
Coefficient d'amortissement :
 (3.21) (3.21)
· La réponse indicielle la plus rapide et sans
dépassement pour un système du second ordre, est du type
apériodique critique. Ce type de réponse est obtenu pour un
coefficient d'amortissement  =1. Ainsi, pour la fonction de transfert Sv(p) : =1. Ainsi, pour la fonction de transfert Sv(p) :
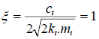 (3.22) (3.22)
 (3.23) (3.23)
· Avec  =1, le polynôme du dénominateur de la fonction de transfert
Sv(p) possède un discriminant nul et donc une racine
réelle double =1, le polynôme du dénominateur de la fonction de transfert
Sv(p) possède un discriminant nul et donc une racine
réelle double 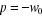 . Il s'écrit sous la forme : . Il s'écrit sous la forme :
 (3.24) (3.24)
Ainsi :
 (3.25) (3.25)
· La constante de temps Tsv
s'exprime :
 (3.26) (3.26)
 (3.27) (3.27)
D'où :
 (3.28) (3.28)
| 


