|
REPUBLIQUE DEMOCRATIQUE DU CONGO
MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET
UNIVERSITAIRE
INSTITUT SUPERIEUR DE TECHNIQUES
APPLIQUEES
« I.S.T.A»
B.P. 6593 KIN 31
SECTION : MECANIQUE
I.S.T.A / BARUMBU
ANALYSE DU COMPORTEMENT DE LA SERVOVALVE
ELECTROHYDRAULIQUE LORS DE FREINAGE
DES ROUES D'UN AVION.
(Cas de Boeing 737-NG)
MENGAWAKU JEAN
Travail de fin de cycle présenté et
défendu en vue de l'obtention du Diplôme d'Ingénieur
technicien en Mécanique
Option : Mécanique d'Aviation
Directeur : Ir. KAWENDE YEMBA Augustin
Ingénieur en Génie
Mécanique
Année Académique 2009-2010
EPIGRAPHE
« La fonction échelon est une abstraction
mathématique. En réalité, aucun signal physique ne peut
subir un accroissement fini en un temps infiniment court. C'est-à-dire,
la grandeur d'entrée met donc toujours un certain temps,
éventuellement très petit mais jamais nul, pour passer de
zéro à xo »
Pierre André Parette et Philippe Robert
REMERCIEMENTS
A seuil de ce travail qui marque la fin de nos études
du premier cycle, nous reconnaissons avoir bénéficie au sein de
l'Institut Supérieur de Techniques Appliquées (ISTA) une
éducation intellectuelle.
Nous remerciements s'adressent aussi aux autorités
académiques, en particulier à Monsieur le Directeur
Général KATANGA-wa-KATANGA et à tout le corps professoral
de l'Institut Supérieur de Techniques Appliquées (ISTA) pour nous
avoir transmis les connaissances avec conscience professionnelle.
A ce terme, nous remercions plus particulièrement notre
Directeur Assistant KAWENDE YEMBA Augustin Ingénieur en
mécanique, pour ses sages conseils, ses directives et sa
générosité qui nous ont permis d'arriver au bout du
présent travail.
Nous remercions, le physicien SEKE VANGU Max, qui,
malgré ses multiples occupations, a bien voulu accepter d'être
encadreur de ce travail.
Nos remerciements s'adressent :
A mon épouse NZOLA Niclette, et mon fils
MENGA Exaudie;
A mon défunt père MIEZI PEDRO ;
A mes mamans : SIVI MARIE et MENDU HELENE ;
A mes parrains : MWANANGULU Vicky et PINDI Nicole, et
leurs enfants Emmanuel et Christopher ;
A mes frères et soeurs : LOWA SIMON, MBIYAVANGA
PEDRO, MIEZI PEDRO, MAVINDA SEBASTIEN, NGUNGA RACHEL, LUZALA ILITO, MAKIESE
MONIQUE, NSAMBA FLAVIE et pour leurs contributions financières et
morales, d'une façon ou d'une autre à ma réussite.
Nous n'oublions pas de remercier nos compagnons de lutte,
KAKONDI DIALO, MAKOLA LOLO, NGOLO KITIAKA, MUKULUPI KINGAMBO, MONGANZA TANZEY
etc. pour la vie estudiantine d'ensemble, de leur collaboration et esprit de
conquête.
MENGAWAKU JEAN
PLAN DU TRAVAIL
EPIGRAPHE
i
REMERCIEMENTS
ii
PLAN DU TRAVAIL
iv
NOTATIONS GENERALES
viii
INTRODUCTION GENERALE
1
I. Problématique
1
II. Objectif
2
III. Méthodologie
3
IV. Subdivision du Travail
3
V. Difficultés rencontrées
3
CHAPITRE I : GENERALITES SUR LE SYSTEME DE
FREINAGE DES AVIONS
4
I.1. Introduction
4
I.2. Les roues d'avion
6
I.3. Le frein
6
I.3.1. Types des freins
6
I.3.1.1. Frein à disque
7
I.3.1.2. Frein à disque en carbone
(carbone-carbone)
8
I.1.3.2.1. Puits de chaleur
8
I.1.3.2.2. Principe de fonctionnement
9
I.1.3.2.3. Avantages du frein carbone
9
I.3.1.3. Frein à disque en
céramique
10
I.3.2. Frein à tambour
10
I.4. Constitution des freins
11
I.3.1. Sécurité de freinage
13
I.3.2. Paramètres mathématique
13
I.3.2.1. Calcul de la vitesse de glissement
14
I.3.2.2. Expression de couple de freinage entre
surfaces en regard
15
I.3.2.3. Couple total
16
I.3.2.4. Décélération ()
17
I.4. Commande de freinage
18
I.4.1. Commande classique
18
I.4.2. Commande automatique
19
I.4.2.1. Les modes LO, MED et MAX
21
I.4.2.2. Le mode normal
21
I.4.2.3. Le mode alternatif
21
I.5. Le système de régulation de
freinage
22
CHAPITRE II : GENERALITE SUR LES SYSTEMES
ASSERVIS
24
II.1. Définition de l'automatique
24
II.2. Notion de système
24
II.2.1. Nécessite de la boucle
fermée
25
II.2. Equations d'un système
linéaire
25
II.2.1. Introduction
26
III.2.2. Exemples
26
II.3. Fonction de transfert d'un système
linéaire
27
II.4. Réponse temporelle des
systèmes
28
II.5. Les différentes entrées
classiques
28
II.5.1. L'échelon
28
II.5.2. La rampe
29
II.5.3. L'impulsion
30
II.6. Réponse d'un système
30
II.6.1. Réponse d'un système du
premier ordre
30
II.6.1. Réponse d'un système du
second ordre
33
II.7. Performances d'un système asservi
37
II.7.1. Stabilité des systèmes
linéaires asservis
37
II.7.1.1. Critère mathématique de
stabilité
38
II.7.1.2. Critère algébrique de
ROUTH
38
II.7.1.3. Tableau de Routh
39
II.7.2. Précision des systèmes
linéaires asservis
39
II.7.2.1. Erreur de position (Erreur statique)
40
II.7.3. Rapidité des systèmes
régulés
41
II.7.3.1. Temps de réponse
41
II.7.3.2. Temps de monté
41
II.7.3.3. Dépassement maximal
44
CHAPITRE III : SERVOVALVE
ELECTROHYDRAULIQUE
45
III.1. Définition
45
III.2. Classification de la servovalve
45
III.2.1. Etage hydraulique pilote
46
III.3. Constitution de la servovalve
47
III.3.1. Architecture d'une servovalve à
deux étages
49
III.4. Etude simplifiée de la servovalve
électro-hydraulique
50
II.4.1 Equation du moteur couple
50
III.4.2. Système buse-palette
50
III.3.3. Tiroir du distributeur
51
III.4. Principe fondamental de la dynamique (PFD)
appliqué au tiroir
52
III.5. Fonction de transfert de la servovalve
54
CHAPITRE IV : ANALYSE DU COMPORTEMENT DU
SERVOVALVE LORS DE FREINAGE
57
IV.1. Analyse du système
57
IV.2. Système asservi
59
IV.3. Mise en équation des
éléments du système de freinage en mode normal
59
IV.4. Schéma fonctionnel du système
de freinage d'un avion
61
IV.5. Comportement du système de freinage en
boucle fermée
62
IV.5.1. Calcul de stabilité du
système en boucle fermée
63
IV.5.2. Calcul de la précision du
système en boucle fermée
64
IV.5.2.1. Erreur statique ou erreur de position
64
IV.5.3. Calcul de la rapidité du
système en boucle fermée
65
V.6. Simulation du système de freinage par
MATLAB
67
V.6.1. Simulation de systèmes
68
CONCLUSION GENERALE
78
BIBLIOGRAPHIE
83
ANNEXE
85
NOTATIONS GENERALES
: décélération
 : facteur d'amortissement en boucle ouverte : facteur d'amortissement en boucle ouverte
 : facteur d'amortissement en boucle fermée. : facteur d'amortissement en boucle fermée.
CT : couple de frottement total de
freinage
Cf : couple de frottement sur un point
D : diamètre
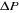 : Différence de pression : Différence de pression
E(t) : entrée
F : effort presseur délivré par l'ensemble des
pistons activés,
F : Force
FA et FB : efforts exercés par
les deux ressorts (A et B)
f : coefficient de frottement de glissement entre les
disques.
G(p) : Fonction de transfert en boucle
ouverte
H(p) : Fonction de transfert en boucle
fermée
Kf : coefficient de frottement
K : gain statique du système
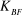 : gain statique en bouclé fermée ; : gain statique en bouclé fermée ;
kt : coefficient de raideur
Ksv : gain statique du servovalve
Kacc : gain statique de
l'accéléromètre
Kc : gain statique du Brake Pedal
Transmitter Unit (BSCU)
mt : masse du tiroir ;
Np : nombre de pistons actifs,
Nd : nombre de disques (stator + rotor) par roue,
Pa : Pression d'alimentation
Ph : pression hydraulique d'alimentation des
pistons,
Re : rayon extérieur de la partie
active de disque de friction
Ri : rayon intérieur de la partie
active de disque de friction
Sp : section d'un piston
S(t) : sortie
St : section du tiroir à ses
extrémités ;
tm : temps de monté
tr : temps de réponse
Va : vitesse de l'avion
Vg : vitesse de glissement
w : vitesse angulaire
 : pulsation propre : pulsation propre
 : pulsation propre en boucle fermée ; : pulsation propre en boucle fermée ;
INTRODUCTION GENERALE
I. Problématique
Le freinage est l'une des fonctions vitales d'un avion, au
même titre que la propulsion ou la sustentation. C'est grâce au
frein que l'avion peut s'immobiliser après l'atterrissage, circuler au
sol en toute sécurité mais également s'arrêter en
cas d'urgence lors d'une interruption de décollage.
Que ce soit sur une bicyclette, une voiture ou un avion, la
problématique est la même : l'énergie cinétique
du véhicule en mouvement est, par suite de frottement transformée
en chaleur pour enfin se dissiper. Pour ce faire, un objet solidaire de la
structure du véhicule, le frein, vient frotter sur les disques en
rotation, ou sur un objet solidaire de la roue. Une différence, de
taille, entre les différents mobiles, réside toutefois dans
l'ordre de grandeur de l'énergie à absorber puisque celle-ci est
proportionnelle à la masse et au carré de la vitesse (½
mv2) du mobile en mouvement.
Les premiers avions n'avaient pas de freins. Ils n'en avaient
pas besoin ; leur masse et leur vitesse de décollage étaient
suffisamment faibles. Puis, la puissance des moteurs aidant, les avions ont
grossi, puis volé de plus en plus vite. On a alors équipé
leurs roues de freins extrapolés de ceux de l'automobile,
c'est-à-dire à tambours avec une commande indépendante par
côté, ce qui permettait aussi de prendre les virages à
basse vitesse.
Avec les réacteurs, les freins sont devenus critiques,
car ils étaient pratiquement les seuls moyens de ralentissement vraiment
efficaces.
Actuellement, les freins à disques permettent d'absorber
une forte énergie avec une masse raisonnable et des matériaux
permettant des températures, en fin de freinage, de plus en plus
élevées.
Parallèlement, la capacité de couple des freins
a nécessité une aide automatique pour éviter les blocages
de roues, puis assurer un rendement de freinage élevé, ce qui a
été possible grâce, en particulier, à l'introduction
de calculateurs électroniques analogiques, puis numériques.
Arrêter un avion lancé au roulage à plus
de 300 km/h en quelques centaines de mètres revient à absorber
une énergie supérieure à 1 milliard de joules en quelques
dizaines de secondes, soit environ 125 mégajoules par roue et frein,
même si le risque est de l'ordre de 1 pour 1 million de
décollages, c'est la mission extrême que doit assumer les roues et
freins.
II. Objectif
L'objectif poursuivi dans ce travail est celui d'analyser
l'asservissement du système de freinage de l'avion et de parvenir
à déterminer la commande du système qui remplisse les
exigences du cahier des charges fonctionnel (analyse fonctionnel,
caractéristique des fonctions de service attendues, et fonction de
service réalisé).
Pour décrire la rapidité de ce système
(temps de monté et de réponse), nous allons utiliser le logiciel
MATLAB, pour mieux interpréter l'analyse du système de
freinage.
III. Méthodologie
Pour arriver à réunir les données
nécessaires à l'élaboration de ce travail, nous avons fait
usage de la méthode analytique, technique documentaire qui consiste
à lire les ouvrages ayant trait au sujet traité :
- La consultation de sites Internet
- La consultation de thèses publiées
- La consultation d'ouvrages aéronautiques
- L'interview auprès des spécialistes du domaine
traité
IV. Subdivision du Travail
Hormis l'Introduction et la conclusion générale,
notre travail se subdivise en quatre chapitres dont :
- Chapitre I : Généralités sur le
système de freinage des avions
- Chapitre II : Généralité sur les
systèmes asservis
- Chapitre III : Servovalve électro-hydraulique
- Chapitre IV : Analyse du comportement de la servovalve
lors de freinage d'un avion.
V. Difficultés
rencontrées
Il s'avère important de souligner d'abord la situation
particulière que connaît notre pays, une situation qui
n'épargne aucun domaine de la vie nationale.
Nous avons été confrontés au
problème de transport pour atteindre le différent centre de
lecture de la ville, des frais pour la navigation sur le web et nos
déplacements vers les aérogares se faisaient dans des conditions
très difficiles.
CHAPITRE I :
GENERALITES SUR LE SYSTEME DE FREINAGE DES AVIONS
I.1. Introduction
Ce chapitre est consacré au freinage des avions et aux
matériels directement impliqués dans cette fonction. Ce sont les
freins, les roues, la commande et la régulation de freinage.
Fonctionnellement, l'ensemble de ces matériels constituent le
système de freinage.(1(*))
Un avion doit avoir la capacité d'effectuer un certain
nombre de manoeuvres au sol.
Avant le vol :
· roulage à faible vitesse, dit taxing, du parking
vers la piste
· roulage à vitesse élevée
précédant le décollage.
Après le vol :
· atterrissage et freinage
· taxing de la piste vers le parking.
Pour toutes ces manoeuvres, il est nécessaire que le
train d'atterrissage, qui supporte le poids de l'avion, permette le roulage et
le freinage par l'intermédiaire de roues équipées de
pneumatiques et de freins.
Au fur et à mesure que les vitesses de décollage
et d'atterrissage augmentaient avec la masse de ces « machines volantes
», leur freinage à l'atterrissage devenait de plus en plus
nécessaire. Ce besoin fut encore accentué par l'avènement
de la propulsion par réaction. Les vitesses ont atteint alors des
valeurs très élevées : près de 250 km/h à
l'atterrissage, de l'ordre de 400 km/h au décollage, parfois
jusqu'à 500. Quant aux masses, elles ont largement dépassé
les 10 tonnes sur certains avions de combat, et les 100 tonnes sur les gros
avions commerciaux. Toutes ces évolutions ont naturellement accru de
façon considérable l'énergie cinétique à
absorber au freinage.
Certes, le freinage des roues n'est pas le seul à
contribuer au freinage de l'avion. En effet, interviennent également le
freinage aérodynamique (traînée de l'avion,
aérofreins et même parachute de queue dans certains cas) et
l'inversion de poussée des réacteurs (apparue dans les
années 1960).
Toutefois le freinage des roues est prépondérant
et devient même le seul efficace dès que la vitesse a
commencé à décroître. Pour des raisons de
sécurité, ni l'inversion de poussée ni les
aérofreins ne sont pris en compte pour le dimensionnement des freins de
roues.
Il faut cependant reconnaître que les roues et freins,
comme les atterrisseurs, constituent un poids mort pendant le vol. Par
conséquent il a existé de tout temps une forte pression des
avionneurs pour obtenir de hautes performances massiques (énergie
absorbée par kg de frein de plus en plus grande). Pour répondre
à cet impératif, les fabricants de freins aéronautiques
ont constamment remis en cause leurs technologies à travers de nombreux
travaux de recherche et d'expérimentation en laboratoire et même
sur avions.
I.2. Les roues d'avion
En fonction des sols sur lesquels l'avion doit opérer,
l'effet d'empreinte (c'est à dire de résistance des sols)
conduit, dès l'origine de la conception de l'avion, à un choix de
pneumatiques (dimension, nombre, disposition géométrique,
pression de gonflage), donc à une dimension des roues et à un
encombrement maximal admissible des freins. Il s'agit là d'un choix de
base pour l'avion, d'autant plus que ce sont les pneumatiques et les roues qui
introduisent les efforts d'atterrissage et de manoeuvre au sol sur les
atterrisseurs, qui eux-mêmes les transmettent à la structure de
l'avion.(2(*))
I.3. Le frein
Un frein est un système permettant de ralentir, voire
d'immobiliser, les pièces en mouvement ou un véhicule en cours de
déplacement.
I.3.1. Types des freins
On trouve différents types de freins utilisés
selon les appareils, les besoins, les époques et les masses en jeu.
(3(*))
· le frein à disques
- en carbone-carbone
- en céramique
- en acier/cuivre
· le frein à tambour
I.3.1.1. Frein à
disque
Comme son nom l'indique, un frein à disque est
simplement un disque (de frein) solidaire de la roue et qui se fait
écraser entre deux plaquettes (solidaires du moyeu, elles sont
fixées dans le cas le plus simple.(4(*))
Disque de freinage

Figure 1.1. Frein à disque
La pièce qui porte les plaquettes de frein
(composée du support et de la garniture) s'appelle l'étrier. Pour
écraser les plaquettes, on utilisé un liquide de frein. Il est
tout sauf de l'eau car l'eau deviendrait vapeur à cause de la pression.
Justement les liquides de freins ont la fâcheuse tendance à
être hydrophiles, c'est pourquoi il faut le changer tous les 2 ans sinon
tu risques de freiner dans le vide avec ta caisse.
La différence entre freins à disque d'avions et
de voiture c'est la taille... sur les voitures, il y a qu'un disque et deux
plaquettes (une de chaque côté donc). Sur les avions, il y a
plusieurs disques et des plaquettes sur tout le pourtour.
I.3.1.2. Frein à
disque en carbone (carbone-carbone)
En termes techniques (définition Snecma), un frein est
constitué d'un "tube de torsion" installé sur l'essieu de l'avion
et d'une «couronne hydraulique». Un «puits de chaleur» est
monté sur cette structure. L'ensemble se loge dans les deux demi-roues
de l'avion.
Disque en carbone

Figure 1.2. Disque en
carbone
I.1.3.2.1. Puits de chaleur
C'est l'empilement des disques de carbone (fig.1.2) : il y en
a, en général, huit ou dix. La moitié tourne avec la roue
: ce sont les rotors. L'autre moitié ne tourne pas : ce sont les
stators. Ils sont montés en alternance. Parce que c'est là que
l'énergie cinétique de l'avion est transformée en
chaleur.
La couronne hydraulique est une pièce en aluminium dans
laquelle sont logés les pistons. Ce sont ces pistons qui, sortant de
leur cavité, poussés par l'huile sous pression vont serrer les
disques les uns contre les autres. En plaçant les pistons en anneau, on
répartit l'effort de pression sur toute la surface des disques.
Le tube de torsion est un cylindre en acier sur lequel sont
fixés les stators. Il encaisse les énormes efforts de torsion qui
s'exercent lorsque rotors et stators sont serrés les uns contre les
autres. Il est solidaire de la couronne hydraulique.
L'ensemble est lié au train d'atterrissage. Les roues
sont constituées de deux demi-roues dissymétriques en aluminium.
La plus grande demi-roue est donc glissée dans le pneu
non gonflé, puis l'autre moitié est solidement vissée. Le
pneu est ensuite gonflé à l'azote à une pression de bars
déterminé du fabricant. Finalement, l'ensemble est monté
sur le frein installé sur l'essieu.
I.1.3.2.2. Principe de
fonctionnement
Lorsque le pilote appuie sur la pédale de frein, son
ordre est traité et transmis par le système de régulation
de freinage. Celui-ci impose au fluide hydraulique de pousser les pistons avec
une pression bien précise(voir cahier de charge). Les disques sont alors
serrés plus ou moins fortement les uns contre les autres : les stators
freinent les rotors et donc la roue.
I.1.3.2.3. Avantages du
frein carbone
· Plus léger ;
· Plus efficace même à haute
température ;
· Nettement plus économique qu'un frein classique,
et
· Il ne vibre pas pendant le freinage.
La grande différence entre une voiture, même
très puissante et un avion est l'ordre de grandeur. Pour une voiture
lancée à 200 km/h, la quantité d'énergie à
dissiper est de l'ordre d'un mégajoule (1 MJ).
Le frein carbone a cet énorme avantage de gagner en
efficacité lorsqu'il chauffe (sans dépasser les limites
préconisées, parce que il absorbe facilement la chaleur) alors
que les disques en métal, c'est l'inverse...
I.3.1.3. Frein à
disque en céramique
Au lieu d'avoir du carbone pour le disque, on a simplement de
la céramique. Comme les céramiques sont souvent des
matériaux réfractaires c'est super pour la chaleur, mais plus
difficile à usiner et ça supporte moins bien les chocs.
I.3.1.4. Frein à disque en acier
Il a une technologie analogique avec le
précédent. A cet effet, le disque est en acier.
I.3.2. Frein à
tambour
Un frein à tambour est aussi solidaire de la roue
(évidemment, sinon on ne freinerait pas), mais la différence
c'est que le système est encapsulé et inaccessible.(5(*))

Figure 1.3. Frein à tambour
C'est toutes 2 mâchoires qui s'écartent, sur leur
face extérieure, on trouve la garniture qui vient frotter contre
l'intérieur du tambour. Donc, il faut un cylindre récepteur de
pression qui écarte les mâchoires contre le tambour.
C'est moins cher à fabriquer, marche moins
bien et peut beaucoup moins facilement contrôler le freinage et
l'état du système.
Pour ce travail, nous avons choisis le frein à disque en
carbone.
I.4. Constitution des
freins
Les disques de frein sont empilés les uns contre les
autres, constituant ce qu'on appelle un "puits de chaleur" en raison de la
température qu'ils peuvent atteindre : jusqu'à 3 000°C pour
un avion freiné à pleine vitesse!
La moitié de ces disques est solidaire de la roue (ou
jante) et tourne avec elle, ce sont les rotors ; l'autre moitié est
solidaire de l'avion par l'intermédiaire de l'essieu et ne tourne pas,
ce sont les stators. Ils sont montés en alternance. Ce sont ainsi les
frottements des disques les uns sur les autres qui assurent le
freinage.(6(*))
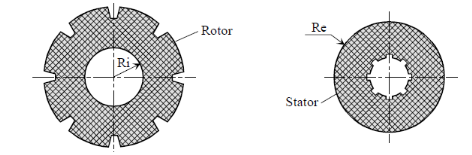
Figure 1.4. Disque de frein
Les disques de friction sont en carbone pour des raisons de
température de fonctionnement et avec une marge d'ordre 1500°C.
Le premier disque sur lequel agissent les pistons à
l'origine des efforts presseurs est un stator solidaire de l'essieu. La figure
ci-dessous.
Figure 1.5. bloc de frein
I.3.1. Sécurité
de freinage
Par mesure de sécurité, le dispositif de
freinage est dédoublé sur chaque roue. Ainsi,
2×Np pistons sont montés sur chaque essieu (Figure.1.5)
mais seulement Np agissent simultanément sur les disques de
frein, les autres Np n'étant utilisés qu'en cas de
défaillance du système de freinage principal.(7(*))
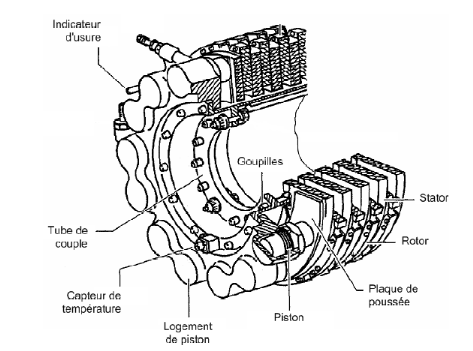
Figure 1.6. Bloc de frein
I.3.2. Paramètres
mathématique
Nous notons :
· Ph : pression hydraulique d'alimentation des
pistons,
· p : pression supposée uniforme entre les deux
faces des disques en contact,
· Sp : section d'un piston,
· Np : nombre de pistons actifs,
· Nd : nombre de disques (stator + rotor) par
roue,
· F : effort presseur délivré par
l'ensemble des pistons activés,
· Ri et Re : respectivement rayons
intérieurs et extérieurs des parties actives des disques de
friction,
· f : coefficient de frottement de glissement entre les
disques.
Hypothèse 1
Nous désignons par Va la vitesse de l'avion
et supposons aucun glissement des roues sur la piste.
I.3.2.1. Calcul de la
vitesse de glissement
En déduire l'expression de la vitesse de glissement
Vg des garnitures de friction en regard pour un point situé
à la distance r de l'axe de rotation.
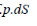
Figure 1.7. Disque de frein
Soit ù la vitesse angulaire de la roue, la vitesse de
glissement à la distance d'un rayon (r) de l'axe de rotation.
est :
 (1.1) (1.1)
or, la vitesse Va de l'avion est :
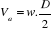 (1.2) (1.2)
D'où
 (1.3) (1.3)
L'effort presseur F auquel est soumise chaque face des disques de
friction en fonction de Ph, Sp et Np.
Hypothèse 2
Nous admettons l'effort F généré par
l'ensemble des pistons actifs est identique sur chacune des faces des disques
de friction.
 (1.4) (1.4)
Hypothèse 3
Supposée p=Cte=uniforme, entre deux disques
en contact. L'effort presseur F qui est normal à la surface de contact,
est fonction de la seule pression de contact p supposée uniforme. Son
expression est :
 (1.5) (1.5)
D'où l'expression de p :
 (1.6) (1.6)
I.3.2.2. Expression de
couple de freinage entre surfaces en regard
Exprimons le moment dM sur l'axe du frein de l'effort
élémentaire dT agissant sur l'élément de surface dS
:
 (1.7) (1.7)
Le couple de freinage C est le moment résultant des
efforts de contact répartis sur toute la surface S.
Ainsi :
 (1.8) (1.8)
p et f sont constant, d'où :
 (1.9) (1.9)
en coordonnées polaires :
 (1.10) (1.10)
Ainsi, pour la surface S(8(*)) :
 (1.11) (1.11)
Et donc :
 (1.12) (1.12)
I.3.2.3. Couple total
Le couple total CT exercé par les Nd
disques du système de freinage d'une roue en fonction de Ph
et des données géométriques et de frottement.
Nous remarquons que le nombre de surfaces de glissement
contribuant au couple CT est : Nd-1.
Ainsi :
 (1.13) (1.13)
 (1.14) (1.14)
Mais :
 (1.15) (1.15)
D'où
 (1.16) (1.16)
En remplaçant dans CT :
 (1.17) (1.17)
I.3.2.4.
Décélération ()
La décélération de l'avion s'exprime
sous la forme :
 (1.18) (1.18)
La décélération étant constante,
Cf doit être équivalent au couple total
CT dû au frottement entre les disques pour une roue.
 (1.19) (1.19)
 (1.20) (1.20)
Or
 (1.21) (1.21)
 (1.22) (1.22)
Le coefficient Kf est donc :
 (1.23) (1.23)
I.4. Commande de freinage
I.4.1. Commande classique
Les commandes classiques de freinage étaient du type
hydraulique : les pédales du pilote commandaient un distributeur
hydraulique par l'intermédiaire, soit d'une liaison mécanique,
soit d'une transmission hydraulique volumétrique. Ceci posait le
problème d'installation de tuyauteries hydrauliques depuis le circuit de
génération, jusqu'au niveau du poste de pilotage, puis du poste
aux freins, ou de la commande mécanique du poste de pilotage à la
soute hydraulique.
La régulation de freinage à une servovalve
asservissant la pression hydraulique à un courant électrique, il
apparaissait beaucoup plus simple d'alimenter directement cette servovalve par
le circuit de génération hydraulique, et de commander sa pression
de sortie par un courant fourni par un transmetteur électrique
actionné par le pédalier.
En supprimant ainsi la nécessité d'amener des
tuyauteries ou des liaisons mécaniques jusqu'au poste de pilotage,
d'où gain en masse, fiabilité et facilité d'installation.
Chaque servovalve comportant deux bobines électriques, l'une pouvait
être affectée à la fonction régulation, l'autre
à la fonction commande de freinage.
Lorsque le freinage n'était pas activé, une
électrovalve en amont des servovalves coupait l'arrivée de
pression. La commande électrique du freinage est plus connue de nos
jours sous sa désignation anglo-saxonne : « brake by
wire ».
I.4.2. Commande automatique
En effet, vu le rôle crucial du freinage, aussi bien au
décollage (freinage de détresse en cas de décollage
refusé) qu'à l'atterrissage, il y a toujours deux commandes de
freinage, dites normale et secours, plus un circuit de freinage parking. La
commande normale est alimentée par un circuit hydraulique, la commande
secours est alimentée par un autre. Le passage d'un circuit sur l'autre
se fait au moyen d'un sélecteur automatique ou manuel, selon
l'avionneur.(9(*))
· le mode normal (Normal Braking)
contrôlé par un ordinateur dénommé BSCU
(Braking/Steering Control Unit). Le BSCU contrôle les servovalves (une
par roue) qui alimentent les pistons presseurs du système de freinage.
La pression hydraulique est fournie par le groupe hydraulique principal.
· le mode alternatif (Alternate braking)
contrôlé par un ordinateur dénommé ABCU (Alternate
Braking Control Unit). Ce mode prend automatiquement la relève du mode
normal s'il y a dysfonctionnement de ce dernier ou si le contrôle
anti-dérapage (Anti-Skid) de l'avion est supprimé. En mode
alternatif, la pression hydraulique est fournie par un groupe hydraulique
secondaire.
En mode normal, il est possible de commander le freinage de
deux façons différentes :
· soit manuellement par appui sur les
pédales de frein, pour chaque pilote, les pédales gauche et
droite sont indépendantes. L'appui sur la pédale gauche agit sur
le freinage des roues du train principal gauche, l'appui sur celle de droite
agit sur le freinage des roues du train principal droit. Les unités de
transmission (Brake Pedal Transmitter Unit) situés sous les
pédales émettent des signaux électriques vers le BSCU ou
vers l'ABCU proportionnels à la course des pédales de frein.
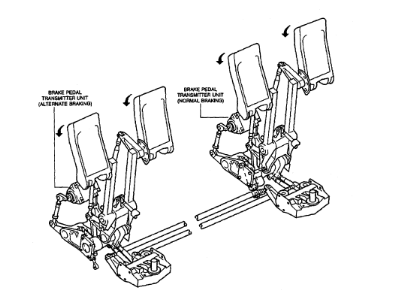
Figure 1.8. : Pédales de frein
Soit automatiquement suivant trois modes de
décélération : LO, MED, MAX. La sélection se fait
à partir de trois boutons situés sur le tableau de bord
(Fig.1.9). Le mode manuel est rétabli si le pilote, en appuyant sur les
pédales de frein, génère une consigne de
décélération supérieure à la consigne de
décélération a du mode automatique
sélectionné.
I.4.2.1. Les modes LO, MED
et MAX
Les modes LO et MED sont utilisés lors de
l'atterrissage. Ils correspondent respectivement à une
décélération de l'avion. Le mode MAX est exclusivement
sélectionné lors du décollage, en cas d'interruption de ce
dernier. Il correspond à une décélération
théorique de -10 ms-2 supérieure à la
décélération maximale de l'avion.
I.4.2.2. Le mode normal
En mode normal (manuel ou automatique), le BSCU contrôle
l'anti-dérapage (Anti Skid) de chaque roue tant que la vitesse de
l'avion est supérieure à 5 m/s.
I.4.2.3. Le mode
alternatif
En mode alternatif, seule la commande manuelle est disponible
avec ou sans anti-dérapage.
Nous s'intéressons au mode de
décélération automatique du mode normal, qui consiste
à asservir en décélération le freinage de l'avion.
La Figure 6 donne le schéma de principe de ce dispositif.
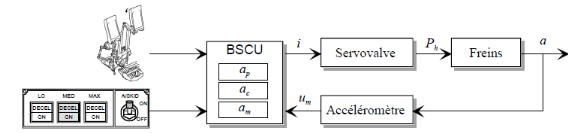
Figure 1.9. Système de freinage
Hypothèse 4
Admettons d'autre part que :
 (1.24) (1.24)
 (1.25) (1.25)
Il s'agit d'une fonction permettant de réaliser, de
façon automatique, l'arrêt de l'avion selon une
décélération constante pré-affichée par le
pilote, avec pour objectif les avantages suivants :
- Une amélioration du confort des passagers lors du
freinage ;
- Une réduction de la charge de travail du
pilote ;
- Une diminution de l'usure des freins et des pneus par la
réalisation de freinage modérés adaptés aux
longueurs de piste disponibles, le recours aux freinages maximaux n'ayant lieu
que lorsque la sécurité est en jeu ;
- Une réduction du temps de mise en oeuvre du freinage
dans les cas de freinage de détresse, par le déclenchement du
freinage maximal sans intervention du pilote.
I.5. Le système de
régulation de freinage
Le système de régulation contrôle en
permanence l'effort de freinage, évitant notamment de bloquer les roues
afin de ne pas provoquer ni dérapage ni éclatement des pneus. La
grandeur physique utilisée comme paramètre de régulation
est la pression de l'huile envoyée dans les pistons qui, serrent plus ou
moins fortement les disques les uns contre les autres.
Tant que l'avion est en vol, le circuit (hydraulique) de
freinage est fermé sur ordre de freinage du pilote.
C'est par l'intermédiaire de servovalves que l'huile
sous pression arrive aux pistons placés dans la couronne hydraulique.
Regroupées sur un support appelé platine, les servovalves
assurent en fait la répartition et le passage de l'huile vers chaque
couronne hydraulique. Une servovalve permet en effet d'ajuster, avec une
certaine précision, la pression de l'huile qu'elle laisse passer. Le
BSCU commande ainsi la servovalve de chaque frein de s'ouvrir plus ou moins
selon la force d'appui transmise par la pédale du pilote, laissant une
pression d'huile plus ou moins grande arriver jusqu'aux freins.
C'est par comparaison de la vitesse de l'avion à celles
des roues que le BSCU contrôle en permanence l'ouverture des servovalves.
CHAPITRE
II : GENERALITE SUR LES SYSTEMES ASSERVIS
II.1. Définition de
l'automatique
Automatique : Qui fonctionne tout seul ou sans intervention
humaine.(10(*))
Dans les systèmes événements discrets. On
parle d'automatisme (séquence d'actions dans le temps). Exemples
d'applications : les distributeurs automatiques, les ascenseurs, le montage
automatique dans le milieu industriel, les feux de croisement, les passages
à niveaux. Dans les systèmes continus pour asservir et/ou
commander des grandeurs physiques de façon précise et sans aide
extérieure. Quelques exemples d'application : le pilotage automatique
d'un avion, frein aéronautique, la vitesse de rotation d'un lecteur CD,
la position du bras d'un robot.(11(*))
II.2. Notion de
système
L'automatique peut s'appliquer à tout ce qui bouge,
fonctionne, se transforme. L'objet d'application de l'automatique est
appelé système. Un système se caractérise
par ses grandeurs d'entrée et de sortie. Les grandeurs d'entrée
sont les grandeurs qui agissent sur le système.
Un système est en boucle ouverte lorsque la commande
est élaborée sans l'aide de la connaissance des grandeurs de
sortie : il n'y a pas de feedback. Dans le cas contraire, le système est
dit en boucle fermée. La commande est alors fonction de la consigne (la
valeur souhaitée en sortie) et de la sortie. Pour observer les grandeurs
de sortie, on utilise des capteurs. C'est l'information de ces capteurs qui va
permettre d'élaborer la commande.
Système
Entrée (commande) sortie
Figure 2.1. Schéma d'un système à
Boucle ouverte
Elaboration de commande
Système
Capteur
Entrée (commande) commande
Sortie
Figure 2.2. Schéma d'un système à
Boucle fermée
Automatique : c'est une science et une technique qui permet de
maîtriser le comportement d'un système (traduit par ses grandeurs
de sortie), en agissant de manière adéquate sur ses grandeurs
d'entrée.
II.2.1. Nécessite de la
boucle fermée
Exceptionnellement, le système de commande peut
opérer en boucle ouverte à partir du seul signal de consigne.
Mais la boucle fermée (contre réaction) est capable de :
- stabiliser un système instable en boucle ouverte
(BO)
- compenser les perturbations externes
- compenser les incertitudes internes au processus
lui-même
Un système de commande peut réaliser deux
fonctions distinctes :
- L'asservissement c'est à dire la poursuite par la
sortie d'une consigne variable dans le temps ;
- la régulation c'est à dire la compensation de
l'effet de perturbations variables sur la sortie (la consigne restant fixe).
II.2. Equations d'un
système linéaire
Dans toute la suite du cours, les systèmes
considères n'auront qu'une entrée et qu'une sortie.
II.2.1. Introduction
Un système est dit linéaire si l'équation
liant la sortie à l'entrée est une équation
différentielle linéaire à coefficients constants. La forme
générale de cette équation différentielle est :
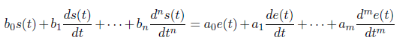
III.2.2. Exemples
R
Soit le circuit RC
C
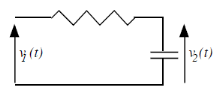
Figure 2.3. Circuit RC
v1 =e(t) et v2=s(t)
Les équations électriques sont :
e(t) = R.i + s(t)


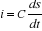
 , introduisant Laplace dans les deux membres, il vient : , introduisant Laplace dans les deux membres, il vient :
 , et la sortie par rapport à l'entrée on aura : , et la sortie par rapport à l'entrée on aura :
 (Système du premier ordre), puisque le dénominateur est
un polynôme du premier degré en p, où* p est
l'opérateur de Laplace. (Système du premier ordre), puisque le dénominateur est
un polynôme du premier degré en p, où* p est
l'opérateur de Laplace.
II.3. Fonction de transfert
d'un système linéaire
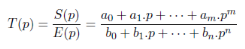
On appelle fonction de transfert ou transmittance d'un
système linéaire le rapport entre la transformée de
Laplace de la sortie sur celle de l'entrée :
(2.1)
C'est une fonction rationnelle. L'ordre du système (qui
est l'ordre de l'équation différentielle) est le degré du
dénominateur de T(p).
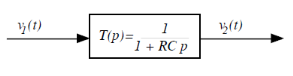
Figure 2.4. Schéma fonctionnel d'un Circuit
RC
On identifiera facilement le fait que c'est un système
d'ordre 1 dont la constante de temps est = RC et de gain statique K = 1.
II.4. Réponse
temporelle des systèmes
On veut caractériser les systèmes d'une part par
leur fonction de transfert et, d'autre part, par leur comportement. Ce dernier
peut être mis en évidence par la réponse s(t) à une
entrée donnée. Classiquement, on peut apprendre beaucoup des
systèmes en observant la réponse aux entrées suivantes
:
- l'impulsion : réponse impulsionnelle
- l'échelon : réponse indicielle
- la rampe : la réponse à une entrée
rampe
- la sinusoïde : réponse
fréquentielle
Nous étudierons aux points suivants les réponses
des systèmes et allons faire le lien entre fonction de transfert et les
réponses (c'est à dire les réponses aux impulsions,
échelon et rampe). Comme dans la suite, nous allons étudier les
systèmes simples et très répandus que sont les
systèmes du premier ordre et du second ordre. De plus, les
méthodes d'étude de ces systèmes se
généralisent facilement aux autres.
II.5. Les
différentes entrées classiques
II.5.1. L'échelon
C'est l'entrée la plus utilisée de toutes. Elle
correspond à un changement brusque de consigne. Cette fonction est
définie par :
  , a R* , a R*
et  
Sa transformée de Laplace est :
 (2.2) (2.2)
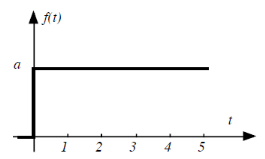
Figure 2.5. La fonction échelon
On appelle échelon unitaire la fonction dont la TL est
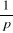 (a = 1). On le note souvent u(t). On appelle réponse indicielle
la réponse à l'échelon unité. (Cfr. Annexe). (a = 1). On le note souvent u(t). On appelle réponse indicielle
la réponse à l'échelon unité. (Cfr. Annexe).
II.5.2. La rampe
La rampe de pente a est la primitive de l'échelon de
hauteur a. Elle est définie par :
 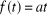
et  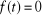
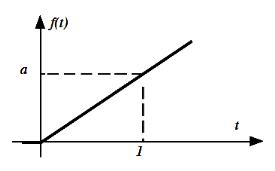
Figue 2.6. La fonction rampe de pente a
Sa transformée de Laplace est définie par :
 (2.3) (2.3)
On peut définir également la rampe unitaire : la
rampe de pente 1.
II.5.3. L'impulsion
L'impulsion unité est, dans l'espace des distributions,
la dérivée de l'échelon unitaire. On l'appelle aussi
impulsion de Dirac.
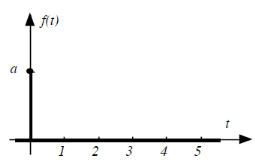
Figure2.7. La fonction impulsion de Dirac de poids
a
II.6. Réponse d'un
système
II.6.1. Réponse d'un
système du premier ordre
1. Mise en équation
 (2.4) (2.4)
T,K : sont des réels positifs
 (2.5) (2.5)
La fonction de transfert s'écrit
 (2.6) (2.6)
K : gain statique, T : constante de temps. (temps
requis pour que le signal de sortie atteigne 63% du signal d'entrée
lorsque cette dernière est un échelon et ce pour un
système du première ordre)
2. Réponses
2.1. Réponse impulsionnelle
(E(p)=1)
 (2.7) (2.7)
En appliquant Laplace inverse, on passe du domaine de Laplace
ou domaine temporel.
 (2.8) (2.8)
s(t)
t
Figure 2.7. Réponse impulsionnelle d'un
système du premier ordre
2.2. Réponse indicielle ( ) )
 (2.9) (2.9)
En utilisant les tables des transformées de Laplace
 (2.10) (2.10)
s(t) K
0,63K
t
T 3T
Figure 2.8. Réponse indicielle d'un système
du premier ordre
T est le temps nécessaire pour atteindre 63% de sa
valeur à l'infinie
3T est le temps nécessaire pour atteindre 95 % de sa
valeur à l'infinie
Le temps de réponse Tr = 3T, est le temps au
bout duquel la sortie atteint sa valeur asymptotique (sa valeur à
l'infinie) à 5 % près.
Preuve
 (2.11) (2.11)


 (2.12) (2.12)
2.3. Réponse à une entrée
rampe ( ) )
 (2.13) (2.13)
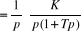
Il est clair que cette sortie et la primitive de la
sortie :
 (2.13) (2.13)
En appliquant Laplace
 (2.14) (2.14)
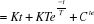
à t=0
s(0)=KT+Cte=0
Cte=-KT
 (2.15) (2.15)
S(t) e(t)=t (entrée)
Asymptote y=K(t-T)
t
Figure 2.9. Réponse d'un système du premier
ordre à entrée rampe
II.6.1. Réponse d'un
système du second ordre
1. Mise en équation
Les systèmes du second ordre sont régis par des
équations différentielles du second degré, leur fonction
de transfert comporte un maximum de deux zéros et deux pôles.
L'équation courante est du type :
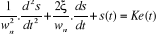 (2.16) (2.16)
Les 3 constantes  : pulsation propre : pulsation propre
 : coefficient ou facteur d'amortissement : coefficient ou facteur d'amortissement
K, gain statique du système
(sont réels et généralement
positifs).
En appliquant Laplace (voir annexe)
 (2.17) (2.17)
La fonction de transfert
 (2.18) (2.18)
 (2.19) (2.19)
2. Réponses
2.1. Réponse indicielle ( ) )
 (2.20) (2.20)
La factorisation du dénominateur est dotée par
le discriminant (delta) du trinôme.
 (2.21) (2.21)
Et
 (2.22) (2.22)
La littérature offre trois cas. 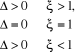
1er cas : 
 (2.23) (2.23)
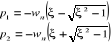 (2.24) (2.24)
S(t)
K 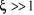
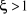
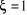
t
t
Figure 2.10. Réponse indicielle d'un système du
second ordre ( ) )
La réponse la plus rapide est observée pour  très proche de 1 très proche de 1
2ème cas : 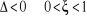
Le trinôme possède alors deux racines complexes
conjuguées qui sont :
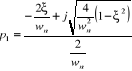 (2.25) (2.25)
 (2.26) (2.26)
 (2.27) (2.27)
S(t) est la réponse du système, constituée
de la différence de deux signaux :
· Le signal k.u(t), échelon de hauteur K
· Le signal sinusoïdal encadré par une enveloppe
e, exponentielle décroissant tendant vers zéro en oscillant.
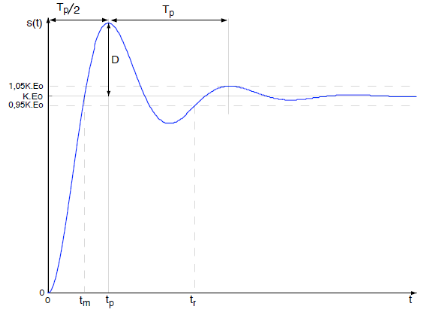
Figure 2.11. Réponse indicielle d'un système du
second ordre à coefficient d'amortissement inférieur à 1
( ) )
La réponse du système est bien dépendant
de 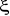
 : Régime amorti : Régime amorti
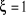 : Régime critique sans oscillation : Régime critique sans oscillation
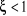 : Régime oscillatoire amorti, : Régime oscillatoire amorti,
II.7. Performances d'un
système asservi
Un système dans son fonctionnement est
caractérisé par un certain nombre de paramètres qu'il
faut :
1. Prévoir (au minimum)
2. Corriger (au mieux)
Un système performant doit être :
- Stable (la stabilité), obligatoirement, sinon on ne
peut l'asservir
- Précis (la précision)
- Rapide (la rapidité)
- Ayant un dépassement nul ou limité.
II.7.1. Stabilité des
systèmes linéaires asservis
Un système est stable si et seulement si à tout
signal borne en entrée, correspond un signal borné en sortie. En
automatique, on définira la stabilité par une des propositions
suivantes : Un système linéaire est stable si est le
seulement si:
- lorsque sa réponse à un échelon prend une
valeur finie en régime permanent,
- lorsque sa réponse à une impulsion tend vers
0,
- lorsque sa réponse à une sinusoïde est une
sinusoïde d'amplitude finie.
Dans la pratique, on exige que le signal de sortie converge
effectivement vers une valeur finie.
D'une manière générale, aucun signal dans
la boucle de régulation ne doit osciller ou tendre vers l'infinie.
Un système asservi est stable si et seulement si sa
fonction de transfert en boucle fermée ne possède aucun
pôle à partie réelle positive.
II.7.1.1. Critère
mathématique de stabilité
Ce système possède un certain nombre
d'inconvénients :
- Sérieux souci pour des polynômes
paramétrés (contient plusieurs paramètres)
- Il est trop binaire et ne laisse pas place à la
notion de la marge de stabilité.
II.7.1.2. Critère
algébrique de ROUTH
Pour savoir si les pôles d'une fonction de transfert
sont à parties réelles négatives, on peut les calculer.
Mais pour des polynômes de degré supérieur à 2, la
résolution devient difficile. Le critère de Routh est un
critère algébrique qui permet de savoir si les racines sont
toutes à partie réelle négative (donc si le système
est stable) sans avoir à calculer ces pôles.
1.1. Equation caractéristique
Dans le cas de l'étude de la stabilité en BF,
l'équation caractéristique est :
 (2.28) (2.28)
Avec :
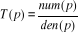 (2.29) (2.29)
Que l'on peut mettre sous la forme :
 (2.30) (2.30)
 (2.31) (2.31)
II.7.1.3. Tableau de
Routh
On forme le tableau suivant :
 (2.32) (2.32)
Avec :
 (2.33) (2.33)
 (2.34) (2.34)
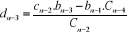 (2.35) (2.35)
Ce tableau est à former jusqu'à ce que l'on ait n
lignes.
Le critère de Routh est le suivant : Si tous les termes
de la première colonne sont strictement positifs, le système est
stable. S'il y a c changements de signes dans la première colonne,
l'équation caractéristique a c racines à parties
réelles positives (et le système est instable).
II.7.2. Précision des
systèmes linéaires asservis
Un système asservis (donc en boucle fermée) sera
d'autant plus précis que sa sortie s(t) est proche de la consigne
(valeur désirée) sd(t). On peut quantifier l'erreur
entre la consigne et la sortie :
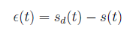 (2.36) (2.36)
Cette erreur sera significative de la précision de
l'asservissement :
- une fois le régime permanent atteint. On parlera de
précision statique ou bien,
- pendant le régime transitoire. On parlera de
précision dynamique.
II.7.2.1. Erreur de
position (Erreur statique)
En boucle ouverte, la fonction de transfert est notée
G(p), en boucle fermée on écrit H(p).
On s'intéresse cette fois à la
différence, en régime permanent entre la consigne et la sortie.
Dans le schéma-bloc ci-dessous, on s'intéresse donc
à :
 (2.37) (2.37)
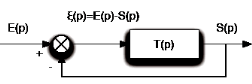
Figure 2.12. Erreur statique
Elle permet d'évaluer l'aptitude d'un système
à se conformer à une consigne constante (régulation). 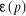 faible, meilleur précision du système. faible, meilleur précision du système.
II.7.3. Rapidité des
systèmes régulés
II.7.3.1. Temps de
réponse
C'est le temps requis pour atteindre la valeur finale de la
sortie à un certain pourcentage près.
  (2.38) (2.38)
On choisit très souvent la notion de réponse
à 5% près.
II.7.3.2. Temps de
monté
Il est préférable au temps de réponse.
C'est le temps requis pour que le signal de sortie franchisse pour la
première fois son asymptote dans le cas évident où ce
phénomène se produit.
Ce qui confère au temps de monté le
caractère d'un bon paramètre pour chiffrer la rapidité
d'un système en boucle fermée.
S(t)
S
t
tm tr
Figure 2.13. Représentation de temps de monté
et de réponse
Considérons un système du second ordre de
fonction de transfert en boucle ouverte G(p) placé dans un boucle de
régulation à retour unitaire, avec :
Système du second ordre
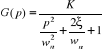 (2.39) (2.39)
Calculons la fonction de transfert en bouclé
fermée de ce système :
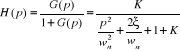 (2.40) (2.40)
 (2.41) (2.41)
Il est donc possible d'utiliser les résultats de
l'étude à propos de l'étude indicielle des systèmes
du second ordre, à condition de poser :
 (2.42) (2.42)
défini comme le gain statique en bouclé
fermée ;
 (2.43) (2.43)
définie comme la pulsation propre en boucle
fermée ;
 (2.44) (2.44)
facteur d'amortissement en boucle fermée.
Pour un échelon à l'entrée du
système en boucle fermée
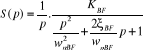 (2.45) (2.45)
Avec :  1 1
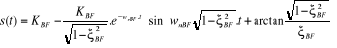 (2.46) (2.46)
Le calcul du temps de monté se fait en
résolvant
 (2.47) (2.47)
Nous aurons :
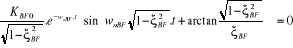 (2.48) (2.48)
Soit :
 (2.49) (2.49)
Nous écrivons :
 (2.50) (2.50)
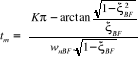 (2.51) (2.51)
La plus petite valeur est visiblement obtenue pour K=1, ce qui
nous conduit :
 (2.52) (2.52)
L'étude de  pour pour  nous est utile. L'analyse de cette fonction nous montre que pour les
valeurs courantes du facteur d'amortissement (0,2 nous est utile. L'analyse de cette fonction nous montre que pour les
valeurs courantes du facteur d'amortissement (0,2 0,8). 2 0,8). 2 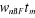 4. 4.
Noue retiendrons de cet encadrement, une valeur
approchée de  : :
 =3 (2.53) =3 (2.53)
 (2.54) (2.54)
 (2.55) (2.55)
II.7.3.3.
Dépassement maximal (système du second ordre, 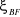 1) 1)
 (2.56) (2.56)
Il est d'autant plus important que  est faible. est faible.
 (2.57) (2.57)
La servovalve par ses propres caractéristiques affecte
la performance globale du système de commande de frein. L'étude
de la fonction transfert d'une boucle d'asservissement sera l'objectif des
points suivants.
CHAPITRE III :
SERVOVALVE ELECTROHYDRAULIQUE
III.1.
Définition
La servovalve électro-hydraulique est un organe de
contrôle proportionnel d'un débit hydraulique ou une pression
hydraulique à sa sortie, modulé par un signal de commande
électrique à son entrée, afin de doser la puissance
délivrée au récepteur hydraulique.(12(*))
Une servovalve électro-hydraulique est un appareil qui
convertit une grandeur électrique (courant ou tension) en une grandeur
hydraulique proportionnelle (débit ou pression).
Servovalve
Source de puissance hydraulique
Courant (I) Pression (P)
Tension (U) Débit (Q)
Figure 3.1. Servovalve
III.2. Classification de la
servovalve
La servovalve à plusieurs étages hydrauliques est
classifiée en deux catégories : les servovalves « en
débit » et les servovalves « en pression » selon la
nature du paramètre hydraulique contrôlé à sa
sortie.
Par ailleurs, la servovalve électrohydraulique est
constituée d'un étage électrique et d'un ou plusieurs
étages hydrauliques, qui assurent la progressivité du
débit et /ou de la pression, proportionnellement à la commande
électrique.
Ainsi, la classification de la servovalve peut être
étendue selon la nature et le nombre des étages hydrauliques. Une
architecture générale de la servovalve peut être
représentée par le schéma suivant.()
 Figure 3.2. Architecture générale d'une
servovalve Figure 3.2. Architecture générale d'une
servovalve
III.2.1. Etage hydraulique
pilote
Cet étage d'amplification d'effort sert à piloter
le distributeur de puissance. Plusieurs types sont distingués selon leur
principe de fonctionnement, parmi lesquels :
· Buse-Palette : ce genre de système est facile
à concevoir mais sensible à la pollution qui produit une panne
critique (embarquement de l'actionneur).
· Jet oscillant (injecteur-buse) : ce type d'étage
est difficile à concevoir et plus résistant à la pollution
qui produit une panne moins critique (perte de performance de l'asservissement
en position de l'actionneur).
· Déflecteur (jet dévié) : cette
technologie a permis à son concepteur de contourner le brevet de jet
oscillant. L'effet de pollution est similaire à celui de la technologie
jet oscillant.
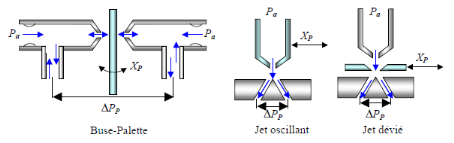
Figure 3.3. Différents types d'étage
hydraulique pilote (1er étage)
Pour notre analyse, nous allons étudier la servovalve
électro-hydraulique à buse-palette.
III.3. Constitution de la
servovalve
Elle est constituée d'un, deux ou trois étages
suivant que le moteur couple électrique pilote directement l'organe de
puissance hydraulique (buse-palette), ou qu'il y a un, deux ou trois
étages d'amplification hydraulique intermédiaire.(13(*))
La servovalve la plus utilisée est la servovalve en
débit ou pression à 2 étages. Elle est constituée
de trois éléments :
· un actionneur pilote de type moteur-couple
électrique ;
· un amplificateur hydraulique constitué d'un
mécanisme buse-palette ;
· un tiroir de distribution.
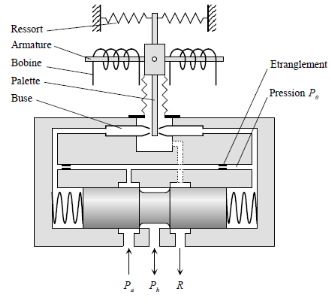
Figure : 3.4. Servovalve simplifiée
L'armature du moteur-couple à courant continu se
prolonge dans l'entrefer d'un circuit magnétique. Le passage d'un
courant continu dans les deux bobines situées de part et d'autre de
l'armature provoque le basculement de cette dernière d'un angle
è.
L'armature est solidaire d'une palette plongeant dans
l'amplificateur hydraulique et dont l'extrémité est située
entre deux buses. Le mouvement de rotation de l'ensemble armature-palette vient
étrangler le débit fluide traversant l'une ou l'autre des buses.
La pression différentielle ainsi créée se répercute
aux deux extrémités du tiroir du distributeur et provoque son
déplacement.
Ce tiroir possède trois orifices de contrôle,
Pa (Alimentation), Ph (Utilisation), R (Retour à
la bâche). La pression Ph est proportionnelle au
déplacement du tiroir compté à partir de la position
zéro (position du milieu).
A titre indicatif, le diamètre d des buses est de
l'ordre de quelques dixièmes de millimètres et l'écart e
entre la buse et la palette de l'ordre de quelques centièmes de
millimètres.
Comme le travail est mené sur une servovalve « en
débit » à deux étages hydrauliques, son architecture
et son fonctionnement sont détaillés ci-après.
III.3.1. Architecture d'une
servovalve à deux étages
Une servovalve à deux étages comporte
généralement un organe électrique (moteur
électrique), un étage hydraulique pilote (étage
d'amplification) et un étage hydraulique de puissance (étage de
distribution) avec un système de rétroaction (asservissement en
position), qui sont présentés dans la Figure.
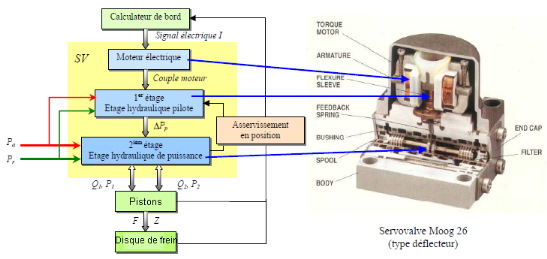
Figure 3.5. Architecture d'une servovalve à deux
étages
III.4. Etude
simplifiée de la servovalve électro-hydraulique
II.4.1 Equation du moteur
couple
A l'état repos, l'intensité et l'angle de
décalage de la palette sont nul.
Le courant traversant les bobines génère un
couple moteur :
Cm(t)= Km.i(t) (3.1)
Deux ressorts, de coefficient de raideur k1,
exercent un couple résistant Cr.
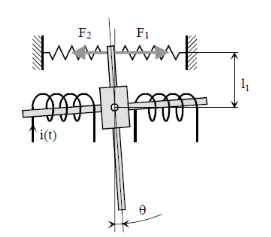
Figure 3.6. Moteur couple
III.4.2. Système
buse-palette
Les sections de fuite entre la buse et la palette sont
identiques.
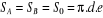 (3.2) (3.2)
De même, les pressions PA et PB
sont égales. Nous avons :
PA= PB=P0 (3.3)
Nous admettons qu'une rotation d'angle de la palette se
traduit par un accroissement (ou une diminution) de la distance
buse-palette.
 (3.3) (3.3)
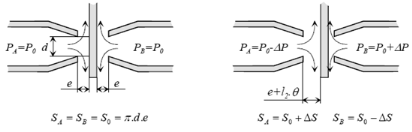
Figure 3.6 : Etat repos Figure 3.7 : Etat
actionné
Cette augmentation (ou diminution) de section entraine une
augmentation (ou diminution de pressions PA et PB proportionnelle àS.
Ainsi :
 (3.4) (3.4)
 (3.5) (3.5)
Avec :
 (3.6) (3.6)
III.3.3. Tiroir du
distributeur
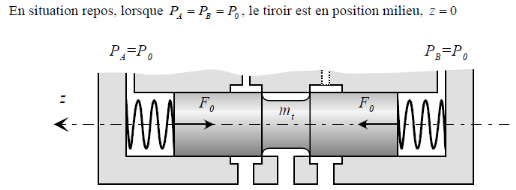
Figure 3.8. : Tiroir en position repos
En position travail, la pression différentielle se
répercute aux extrémités du tiroir et provoque son
déplacement (Figure ).
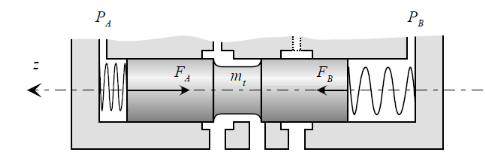
Figure 3.9 : Tiroir en position travail
On utilise les notations suivantes :
· mt : masse du tiroir ;
· St : section du tiroir à ses
extrémités ;
· FA et FB : efforts exercés
par les deux ressorts de coefficient de raideur kt montés de
part et d'autre du tiroir du distributeur ;
· ct : coefficient de frottement visqueux
entre tiroir et cylindre.
III.4. Principe fondamental
de la dynamique (PFD) appliqué au tiroir
Le principe fondamental de la dynamique (PFD) appliqué
au tiroir du distributeur et en déduire la forme canonique de la
fonction de transfert :
· Théorème de la résultante
dynamique :
- En projectant sur 
 (3.7) (3.7)
Les forces des ressorts s'expriment :
 (3.8) (3.8)
 (3.9) (3.9)
Les pressions aux extrémités du tirroir
s'expriment :
 (3.10) (3.10)
 (3.11) (3.11)
En remplaçant dans l'équation sur  : :
 (3.12) (3.12)
· Transformée de Laplace de
l'équation :
Nous considérons les conditions suivantes à
t=0
 (3.13) (3.13)
Ainsi, nous pouvons écrire :
 (3.14) (3.14)
· Fonction de transfert
Divisons le numérateur et le dénominateur par
2kt.
· Fonction de transfert sous sa forme canonique :
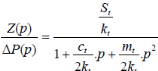 (3.15) (3.15)
D'où le schéma bloc du servovalve peut
s'écrire :
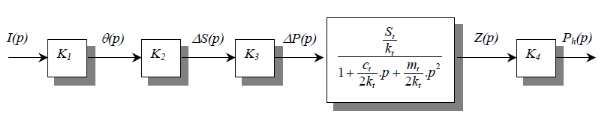
Figure 3.10 : Schéma bloc du servovalve
On admet enfin que la pression d'utilisation
Ph(t)du fluide est proportionnelle au déplacement z(t) du
tiroir :
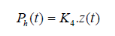 (3.16) (3.16)
III.5. Fonction de
transfert de la servovalve
La fonction de transfert de la servovalve et montrer qu'elle
peut se mettre sous la forme d'un système du second ordre :
 (3.17) (3.17)
· Fonction de transfert sous sa forme canonique :
 (3.18) (3.18)
· Coefficients caractéristiques de la fonction de
transfert du second ordre :
Gain statique :
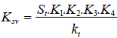 (3.19) (3.19)
Pulsation propre :
 (3.20) (3.20)
Coefficient d'amortissement :
 (3.21) (3.21)
· La réponse indicielle la plus rapide et sans
dépassement pour un système du second ordre, est du type
apériodique critique. Ce type de réponse est obtenu pour un
coefficient d'amortissement  =1. Ainsi, pour la fonction de transfert Sv(p) : =1. Ainsi, pour la fonction de transfert Sv(p) :
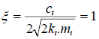 (3.22) (3.22)
 (3.23) (3.23)
· Avec  =1, le polynôme du dénominateur de la fonction de transfert
Sv(p) possède un discriminant nul et donc une racine
réelle double =1, le polynôme du dénominateur de la fonction de transfert
Sv(p) possède un discriminant nul et donc une racine
réelle double 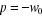 . Il s'écrit sous la forme : . Il s'écrit sous la forme :
 (3.24) (3.24)
Ainsi :
 (3.25) (3.25)
· La constante de temps Tsv
s'exprime :
 (3.26) (3.26)
 (3.27) (3.27)
D'où :
 (3.28) (3.28)
CHAPITRE IV : ANALYSE
DU COMPORTEMENT DE LA SERVOVALVE ELECTRO-HYDRAULIQUE
IV.1. Analyse du
système
Les systèmes asservis sont des systèmes
commandés électromécaniques régis par les lois de
la dynamique, et de l'électricité. La mise en équation
d'un système conduit à un système d'équations
différentielles.(14(*))
Le but de l'analyse d'un asservissement est de parvenir
à déterminer la commande du système qui remplisse les
exigences du cahier des charges fonctionnel (analyse fonctionnel,
caractéristique des fonctions de service attendues, et fonction de
service réalisés).
Le schéma ci-dessous présente la démarche
globale d'étude d'un système asservi, avec deux méthodes
conduisant au diagramme fonctionnel (la méthode théorique qui
passe par la mise en équations, et la méthode
« pratique » qui consiste à effectuer des
essais).
Système matériel asservi
si le système est simple si le
système est complexe
Mise en équation
Système d'équations
Expérimentation
Sollicitation du système par un signal
Analyser (modélisation)
Identification
Schématisation fonctionnelle
(schéma-blocs)
Sollicitation par un signal typique
Comportement fonctionnelle
Réponse du système
Simulation
Réglage et correction, en fonction des performances
souhaitées
Analyse des performances
Figure : 4.1. Démarche globale d'étude
d'un système asservi
Parmi ces deux choix des méthodes, nous avons
souhaité faire notre analyse par la méthode théorique, qui
pourra moins nous coûter que la méthode pratique.
IV.2. Système
asservi
Le système à analyser s'intitule :
servovalve électrohydraulique (lors de freinage des roues)
Le système comprend quatre (4) éléments,
il s'agit :
1. Un calculateur de commande
« BSCU » : Brake Pedal Transmitter Unit ou ABCU :
Alternate Braking Control Unit, selon le mode de commande.
2. Une servovalve
3. Un bloc de frein
4. Un capteur
« accéléromètre »
IV.3. Mise en
équation des éléments du système de freinage en
mode normal (15(*))
1. BSCU : Brake Pedal Transmitter Unit
 (4.1) (4.1)
 (4.2) (4.2)
 : Sortie : Sortie
 : Entrée : Entrée
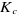 : gain statique du BSCU : gain statique du BSCU
2. Servovalve électrohydraulique
La fonction de transfert de la servovalve en boucle ouverte
est donnée par la relation :
 (4.3) (4.3)
 : gain statique de la servovalve : gain statique de la servovalve
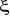 : coefficient d'amortissement : coefficient d'amortissement
 : pulsation propre : pulsation propre
3. Bloc de frein
 (4.4) (4.4)
 (4.5) (4.5)
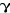 : Accélération des roues : Accélération des roues
 : Coefficient de frottement des disques : Coefficient de frottement des disques
 : Pression hydraulique (sortant du servovalve) : Pression hydraulique (sortant du servovalve)
4. Accéléromètre
La centrale inertielle contient des
accéléromètres qui permettent de mesurer les
accélérations suivant les trois directions xa, ya, za d'un
repère lié à l'avion.
L'accéléromètre renvoie au BSCU un signal
électrique ua(t) image de l'accélération  (t) suivant la direction xa. La tension ua(t) est convertie
en grandeur numérique am par un convertisseur
analogique-numérique et rangée dans la mémoire du BSCU. (t) suivant la direction xa. La tension ua(t) est convertie
en grandeur numérique am par un convertisseur
analogique-numérique et rangée dans la mémoire du BSCU.
 (4.6) (4.6)
 (4.7) (4.7)
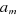 : sortie : sortie
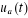 : entrée : entrée
 : gain statique de l'accéléromètre : gain statique de l'accéléromètre
IV.4. Schéma
fonctionnel du système de freinage des roues d'un avion
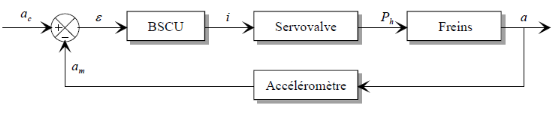
Figure 4.2. La boucle d'asservissement
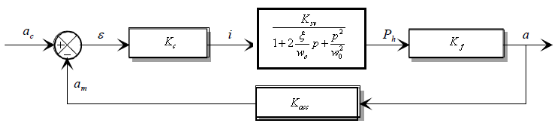
Figure 4.3. Schéma bloc
D'où la fonction de transfert en boucle fermée du
système s'écrira :
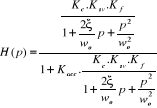 (4.8) (4.8)
Cherchons le dénominateur commun :
 (4.9) (4.9)
Posons :
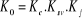 (4.10) (4.10)
 (4.11) (4.11)
D'où l'équation de la fonction de transfert en
boucle fermée devient :
 (4.12) (4.12)
IV.5. Comportement du
système de freinage en boucle fermée
Dans ce point, nous allons faire l'analyse du système,
voir si le système est performant (stable, précis, et rapide), ou
non pour le corriger. (16(*))
IV.5.1. Calcul de
stabilité du système en boucle fermée
La théorie enseigne que, un système du second
ordre sera toujours stable en boucle ouverte qu'en boucle fermée lorsque
la branche retour est constituée que par un gain.
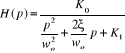 (4.13) (4.13)
Parmi les critères de stabilité, nous avons
utilisés le critère de Routh qui dit :: Si tous les termes
de la première colonne sont strictement positifs, le système est
stable. S'il y a changements de signes dans la première colonne,
l'équation caractéristique à parties réelles
positives (et le système est instable).
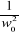 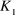
 0 (4.14) 0 (4.14)
 0 0
Or, nous avons posé :
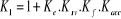
et
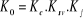
Le système est bel et bien stable à
condition que : 0 0
C'est-à-dire : 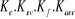 0 0 
IV.5.2. Calcul de la
précision du système en boucle fermée
IV.5.2.1. Erreur statique
ou erreur de position
 (4.15) (4.15)
 (4.16) (4.16)
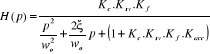 (4.17) (4.17)
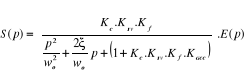 (4.18) (4.18)
Dans ce cas :
 (4.19) (4.19)
Calculons l'erreur de position à l'entrée
Echelon unitaire E(p)=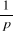
 (4.20) (4.20)
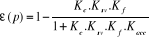 (4.21) (4.21)
Or, nous avons posés : 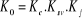
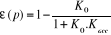 (4.22) (4.22)
Cette précision peut être régler
avec : K0.Kacc, donc il faut maximiser :  . .
Plus que l'erreur est petite, la précision sera
meilleur.
Hypothèse 5
Si l'accéléromètre est de gain
unité (Kacc = 1)
Avec :
 (4.23) (4.23)
Donnons des valeurs à K0
Avec : K0 = 1 :  = 50 % = 50 %
K0 = 9 : 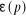 = 10 % = 10 %
K0 = 19 :  = 5 % = 5 %
K0 = 99 :  = 1 % = 1 %
IV.5.3. Calcul de la
rapidité du système en boucle fermée
 (4.24) (4.24)
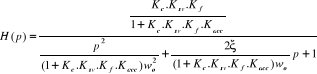 (4.25) (4.25)
 (4.26) (4.26)
défini comme le gain statique en bouclé
fermée ;
 (4.27) (4.27)
définie comme la pulsation propre en boucle
fermée ;
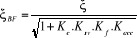 (2.28) (2.28)
facteur d'amortissement en boucle fermée.
D'où, l'équation générale du
système en boucle fermée devient :
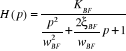 (4.29) (4.29)
Pour décrire la rapide de ce système (temps de
monté et de réponse), nous avons utilisé un logiciel
« MATLAB », qui sera l'objet du point suivant.
Par là, nous allons voir comment les courbes sont
tracées, et puis interprétées.
IV.6. Simulation du
système de freinage des roues par MATLAB
IV.6.1. Introduction
MATLAB (MATrix
LABoratory) est un logiciel de calcul numérique produit
par MathWorks. Il consiste en un langage interprété qui
s'exécute dans une fenêtre dite d'exécution.(17(*))
SIMULINK : c'est l'extension graphique
de MATLAB permettant la modélisation et la simulation de systèmes
dynamiques en utilisant une représentation de type graphique
(schéma bloc).
Avec matlab il n'est plus besoin de disposer
d'équipement encombrant et coûteux pour expérimenter et
mettre au point ses connaissances, ses cours, ses exercices et
problèmes. Un ordinateur portable équipé du logiciel
adéquat suffit.
Avec matlab on peut simuler rapidement n'importe quel
système puis procéder à la correction en boucle
fermée avec un correcteur approprié. Un computer
équipé du logiciel matlab adéquat suffit :
équipements encombrant et coûteux ne sont plus un problème
pour des expériences.
On peut utiliser MATLAB soit :
1. En mode en ligne; c'est-à-dire saisir des commandes
dans la fenêtre d'exécution au fur à mesure. Le mode en
ligne permet d'obtenir des résultats simples qui ne sont pas
sauvegardés.
2. En mode programmation; en écrivant dans des
fichiers séparés  l'enchaînement des commandes. Ces fichiers s'appellent des scripts
et on les construit à la l'aide de n'importe quel éditeur de
texte. Le mode programmation, lui, permet de développer des
applications très complexes. l'enchaînement des commandes. Ces fichiers s'appellent des scripts
et on les construit à la l'aide de n'importe quel éditeur de
texte. Le mode programmation, lui, permet de développer des
applications très complexes.
L'utilisateur peut entrer multiples commandes ou
équations mathématiques après le signe
>>, qui apparaît au coté gauche de la
fenêtre. Pour exécuter une opération, il faut toujours
appuyer sur la touche enter du clavier. De plus, il faut
terminer l'opération par un point-
virgule « ; » sinon, toutes les étapes du
calcul seront affichées sur l'écran.
IV.6.2. Simulation de
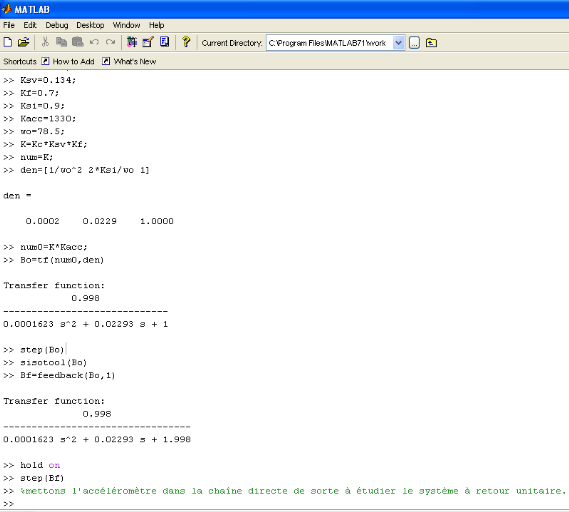
systèmes de freinage par MATLAB (18(*))
Hypothèse simplificatrice :
Le capteur (l'accéléromètre est
placé dans la chaîne directe) de façon à
étudier un système à retour unitaire.
Cahier de charge (paramètres
intrinsèques du système à régler).
Kc = 8 mA
Ksv = 1.34. 10-4 m3/s/mA
Kf = 0.7
Kacc = 1330 mA/m
 = 0,9 = 0,9
 = 78.5 Rad/s = 78.5 Rad/s
IV.6.2.1. Programmation du système de transfert
en boucle ouverte
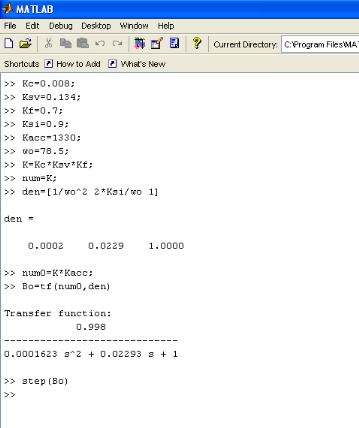
La fonction de transfert est notée par :

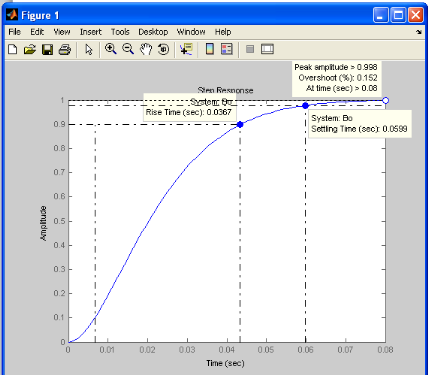
En boucle ouverte la réponse est
représentée ci-dessus.
Commentaire :
- Rise time (temps de montée) 0.0367 secondes,
- Setting time (temps de réponse ou d'établissement
du régime stationnaire) 0.0599 secondes.
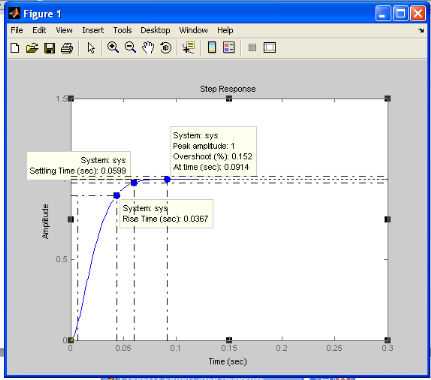
Le dépassement est de 0.152 %
Mais, la boucle ouverte n'est pas bienvenue pour une étude
en asservissement, parce que le système n'est pas contrôlé.
Nous devons passer d'un système en boucle ouverte à un
système en boucle fermée.
IV.6.2.2. Programmation du système en Boucle
Fermée non compensée
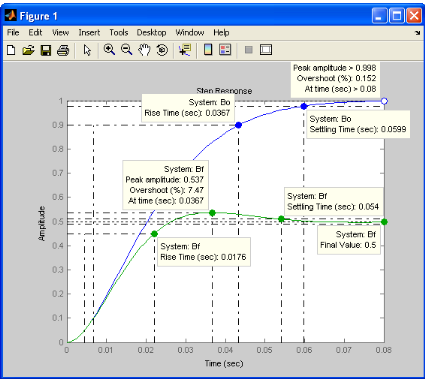
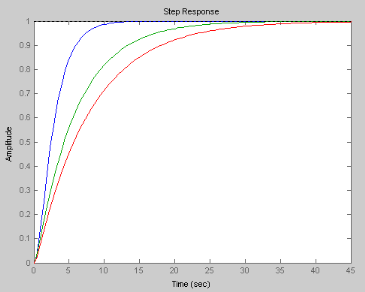
Commentaire
Bleu : Boucle ouverte
Vert : boucle fermée non compensée avec
l'accéléromètre sur la chaine directe de façon
à étudier un système à retour unitaire.
D'où l'écart est de 1-0.5 = 0.5 soit 50 %
d'imprécision, il nous faut obligatoirement un système
correcteur.
IV.6.2.3. Choix du correcteur
Le correcteur a été choisi selon la
théorie de compensation pôle-zéro ; qui consiste
à créer des pôles et des zéros du correcteur qui se
simplifient avec ceux du système à corriger.(19(*))
L'objectif de ce point est de présenter une
première technique de synthèse des régulateurs PI, PD et
PID, une méthode permettant de calculer les paramètres Kp, Ti et
Td selon le type de régulateur choisi.
On se restreindra à la présentation de la
méthode de synthèse dite de compensation pôle-zéro.
La technique de la compensation pôle-zéro consiste à placer
un zéro du régulateur Gc(s) situé au même endroit
qu'un des pôles du système à régler.
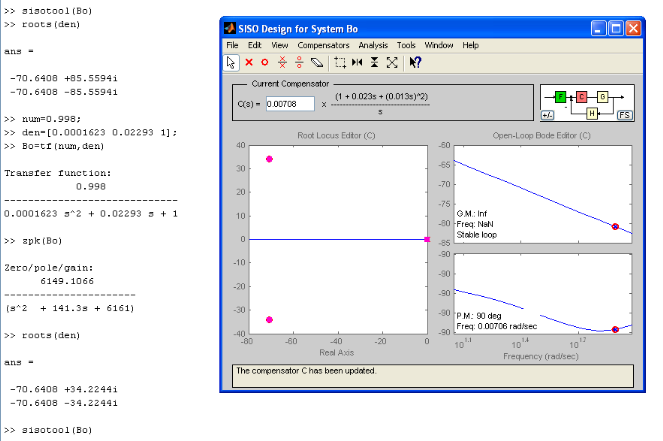
La fonction de transfert du système en boucle ouverte
avec MATLAB sera :
Programmation
>> num=0.998;
>> den=[0.0001623 0.02293 1];
>> Bo=tf(num,den)
Transfer function:
0.998
-----------------------------
0.0001623 s^2 + 0.02293 s + 1
>> zpk(Bo)
Zero/pole/gain:
6149.1066
----------------------
(s^2 + 141.3s + 6161)
>> roots(den)
ans =
-70.6408 +34.2244i
-70.6408 -34.2244i
Choix du correcteur selon la compensation pôle
zéro (ça se fait toujours en boucle ouverte)
Transfer function:
0.998
-----------------------------
0.0001623 s^2 + 0.02293 s + 1
>> sys1=Bo;
Le compensateur est dimensionné en se basant sur la
fonction ci-haut. Et on écrira :
0.0001623 s^2 + 0.02293 s + 1
0.002293s
Par Matlab il on tapera :
>> num1=[0.0001623 0.02293 1];
>> den1=[0.02293 0];
>> sys2=tf(num1,den1)
Transfer function Corrector G(s):
0.0001623 s^2 + 0.02293 s + 1
-----------------------------
0.02293 s
En multipliant le bloc correcteur et celui du système
à régler, on aura par Matlab :
>> sys=sys1*sys2
Transfer function:
0.000162 s^2 + 0.02288 s + 0.998
------------------------------------------
3.722e-006 s^3 + 0.0005258 s^2 + 0.02293 s
Et en boucle fermée Matlab
donnera:
>> sys3=feedback(sys,1)
Transfer function:
0.000162 s^2 + 0.02288 s + 0.998
--------------------------------------------------
3.722e-006 s^3 + 0.0006878 s^2 + 0.04581 s +
0.998
Un système du troisième ordre et de
degré relatif 3-2=1. D'où vient que le système se
comportera comme celui du premier ordre n'ayant naturellement pas de
dépassement.
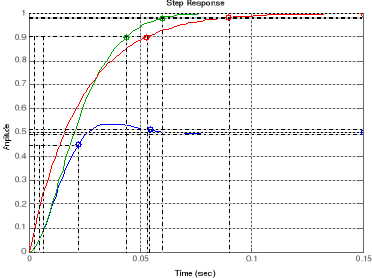
.
CONCLUSION GENERALE
Après modélisation et simulation, la boucle
ouverte, les boucles fermées compensée et non sont
représentées ci-dessous :
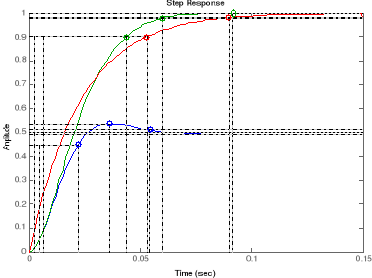
Temps de montée (Rise time) de 10 à 90 %
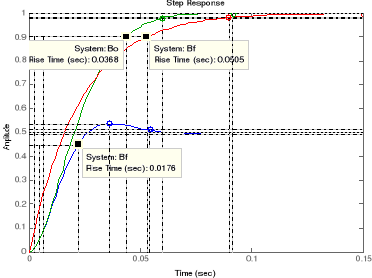
Temps de réponse (Setting times) ou temps
d'établissement du régime stationnaire à 2%
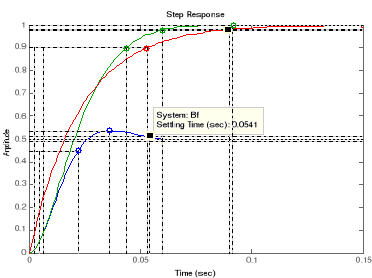
Tableau récapitulatif.
>> num=0.998;
>> den=[0.0001623 0.02293 1];
>> Bo=tf(num,den);
>> sys1=feedback(Bo,1)
Transfer function:
0.998
---------------------------------
0.0001623 s^2 + 0.02293 s + 1.998
>> num2=[0.0001623 0.02293 1];
>> den2=[0.02293 0];
>> corr=tf(num2,den2)
Transfer function:
0.0001623 s^2 + 0.02293 s + 1
-----------------------------
0.02293 s
>> sys=corr*sys1
Transfer function:
0.000162 s^2 + 0.02288 s + 0.998
------------------------------------------
3.722e-006 s^3 + 0.0005258 s^2 + 0.04581 s
>> syscomp=feedback(sys,1)
Transfer function:
0.000162 s^2 + 0.02288 s + 0.998
-------------------------------------------------
3.722e-006 s^3 + 0.0006878 s^2 + 0.0687 s +
0.998
Etude comparative de performances
|
Système
|
Fonction de transfert
|
Pôles, zéro et gain
|
Régime
|
Rapidité
|
Dépas %
|
Précision
Ecart de position
|
|
Tm 0 à 90 %
|
Tr 2%
|
|
BO
|
0.998
------------------------------------------
0.0001623 s^2 + 0.02293 s + 1
|
-70.6500 #177; 34.1991i
Pas de zéro
6149.1066
|
Oscillatoire
|
0.0368
|
0.0599
|
0.153
|
0%
|
|
BF
|
0.998
-----------------------------------------------
0.0001623 s^2 + 0.02293 s + 1.998
|
-70.6408#177;85.5594i
Pas de zéro.
6149.1066
|
oscillatoire
|
0.0176
|
0.0541
|
7.45
|
50%
|
|
BF C
|
0.000162 s^2 + 0.02288 s + 0.998
----------------------------------------------------------------------
3.722e-006 s^3 + 0.0006878 s^2 + 0.0687 s + 0.998
|
-70.6500 #177;34.1991i
-70.6500 #177;34.1991i et -17.2200
43.5238
|
non oscillatoire
|
0.0505
|
0.0899
|
Non
|
0%
|
BIBLIOGRAPHIE
I. OUVRAGES
Brian D. Hahn and Daniel T. Valentine, Essential MATLAB®
for Engineers and Scientists,Third edition,2007.
Catalog, "Transfer Function For MOOG Servovalves", MOOG
Technical Bulletin 103, MOOG Inc. Controls Division, East Aurora, Ny
14052.
G. Rabie and M. Lebrun, "Modélisation par Les Graphes
à Liens et Simulation d'une Servovalve Electrohydraulique à Deux
Etages", R.A.I.R.O Automatique Systems Analysis and Control, vol. 15,
n°2, 1981.
Y. Tchouprakov, Commande Hydraulique et Automatismes
Hydrauliques. Moscou, Ed. Mir, 1979.
Jacques Veaux, Les trains d'atterrissage et les systèmes
associés, Edité par le Centre des hautes études de
l'armement Division Histoire de l'armement, 2006.
II. SUPPORTS DE COURS
J.Baillou, J.P.Chemla, B. Gasnier, M.Lethiecq, Cours de
Systèmes Asservis, Polytech'Tours, 2009.
Lionel PREVOST, cours de l'initiation à Matlab,
Université Pierre et Marie Curie, Paris, 2008.
Prof. Michel ETIQUE, cours Régulation automatique,
Ecole d'Ingénierie et de Gestion du canton de Vaud, Suisse, 2007.
III. THESES PUBLIEES
Batoul ATTAR, Modélisation réaliste en conditions
extrêmes des servovalves électrohydrauliques utilisées pour
le guidage et la navire aéronautique et spatiale, Thèse de
Doctorant 2008,INSA de Toulouse, n°ordre 919.
J.-C. Maré, "Mémoire de Doctorat d'état,
Contribution à la Modelisation, la Simulation, l'Identification et la
Commande d'Actionneurs Electrohydrauliques". Lyon, Université Claude
Bernard- Lyon I, 1993.
IV. SITES INTERNET
http://www.aviation-fr.com
http://www.gs2i.fr/fineprint/pdffactory.htm
http://www.google.com/constitution_des_freins.htm
http://www.wikipedia/corrige-UPSTI-2007/ccp-mp.htm
http://www.aero-hesbaye.be/dossiers/PA/PA_ind.htm
ANNEXE


  
* 1 Jacques Veaux, Les trains
d'atterrissage et les systèmes associés, Edité par le
Centre des hautes études de l'armement Division Histoire de l'armement,
2006, p.121-122.
* 2
http://www.aviation-fr.com
* 3 Idem
* 4 www.messier-bugatti.com
* 5 www.aviation-fr.com
* 6
www.wikipedia.com/constitution_des_freins.htm
* 7
www.wikipedia/corrige-UPSTI-2007/ccp-mp.htm
* 8 Notes de cours de
Mathématique, G1/2007, p.130-145.
* 9
http://www.aero-hesbaye.be/dossiers/PA/PA_ind.htm
* 10 Dictionnaire la Rousse
* 11 J.Baillou, J.P.Chemla, B.
Gasnier, M.Lethiecq, Cours de Systèmes Asservis, Polytech'Tours,
2009, p.1-82.
* 12 Batoul ATTAR,
Modélisation réaliste en conditions extrêmes des
servovalves électrohydrauliques utilisées pour le guidage et la
navire aéronautique et spatiale, Thèse de Doctorant
2008,INSA de Toulouse, n°ordre 919, p.5-32.
* 13 J.-C. Maré,
"Mémoire de Doctorat d'état, Contribution à la
Modelisation, la Simulation, l'Identification et la Commande d'Actionneurs
Electrohydrauliques". Lyon, Université Claude Bernard- Lyon I, 1993.
P.33-34.
* 14 Y. Tchouprakov,
Commande Hydraulique et Automatismes Hydrauliques. Moscou, Ed. Mir,
1979, p.103.
* 15 Catalog, "Transfer
Function For MOOG Servovalves", MOOG Technical Bulletin 103, MOOG Inc.
Controls Division, East Aurora, Ny 14052, 1965.
* 16 G. Rabie and M. Lebrun,
"Modélisation par Les Graphes à Liens et Simulation d'une
Servovalve Electrohydraulique à Deux Etages", R.A.I.R.O Automatique
Systems Analysis and Control, vol. 15, n°2, 1981, pp. 97-129.
* 17 Brian D. Hahn and Daniel
T. Valentine, Essential MATLAB® for Engineers and Scientists,Third
edition,,2007, p.1-429.
* 18 Lionel
PREVOST, cours de l'initiation à Matlab, Université Pierre et
Marie Curie, Paris, 2008, p.1-86.
* 19 Note des cours,
Régulation automatique, (MI : M173-REG GE : REGHaute), Ecole
d'Ingénierie et de Gestion du Canton de Vaud, Suisse, mars 2007,
p.161-167.
| 
