II.8. Modélisation neuronale des
systèmes non linéaires :
L'utilisation des réseaux de neurones pour la
modélisation des systèmes non linéaires découle
naturellement des aptitudes de ces derniers à l'approximation et la
généralisation. La détermination du modèle
dynamique d'un système comporte en général les
étapes suivantes
[3] :
> Acquisition des données d'apprentissage et de
test.
> Choix de la structure du modèle.
> Estimation des paramètres du modèle.
> Validation du modèle identifié.
La première étape fournit les données
entrées/sorties susceptibles de permettre l'extraction d'un
modèle de procédé significatif. La deuxième
étape consiste à choisir la structure du modèle
susceptible de représenter la dynamique du système,
l'architecture du réseau de neurones et ses entrées. Les
réseaux multicouches statiques sont les plus utilisés à
cause de la simplicité de leurs algorithmes d'apprentissage et leurs
aptitudes à l'approximation et à la généralisation.
Il n'existe pas de méthodes générales pour le choix du
nombre de neurones sur chaque couche cachée ainsi que le nombre de ces
dernières. Cependant un réseau à une seule couche
cachée est dans la majorité des cas suffisant. En
référence à la théorie des systèmes
linéaires, plusieurs modèles non linéaires ont
été proposés
- Le modèle NFIR : la régression est
composée uniquement des entrées passées.
yà(k) = f (u (k
-1),..., u (k - n)) (II-14)
- Le modèle NARX : dans ce cas la régression est
composée de sorties et entrées
passées.
yà(k) = f
(u (k -1),..., u (k - n),
y (k -1),..., y (k -m))
(II-15)
- Le modèle NOE : la régression est
composée d'entrées et sorties estimées passées.
yà(k) = f (u (k
-1),..., u (k - n), yà (k
-1),..., yà (k -m)) (II-16)
-Le modèle NARMAX : la régression est
composée de sorties et entrées passées Ainsi que d'erreurs
d'estimation.
yà(k) = f
(u(k -1),...,u(k -
n), y(k -1),..., y(k
-m),e(k-1),...,e(k-l)) (II-17)
II.9.Identification des processus par réseaux
de neurones :
Le principe de l'identification par réseau neuronaux
consiste à substituer aux modèles paramétriques classiques
des modèles neuronaux, c'est-à-dire proposer un modèle
établissant une relation entre son entrée et sa sortie et
à déterminer, à partir du couple des signaux
d'entrée-sortie, le comportement du modèle. Deux raisons
importantes nous motivent [2] :
> Prédire le comportement d'un système pour
différentes conditions de fonctionnement.
> Élaborer une loi de commande à appliquer au
processus pour qu'il réalise l'objectif
assigné.
Nous citerons deux techniques d'identification à base de
réseaux de neurones multicouches : la méthode d'identification
directe et la méthode d'identification inverse.
II.9.1. Identification directe :
La figure (II .9) montre le schéma
général d'identification directe d'un processus. Sur cette
figure, le réseau de neurones identificateur RNI est utilisé en
parallèle avec un processus de type boite noire. La sortie du processus,
y, est comparée avec la sortie du réseau de
neurones, y, puis l'erreur e=y-y est utilisée afin
d'affiner les paramètres du système neuronal
[2].
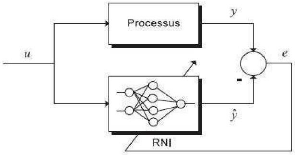
Figure. II.9 .Schéma d'identification
directe d'un processus par réseau de neurones.
Pour considérer l'aspect dynamique du système, on
a le choix d'utiliser les réseaux de neurones récurrents, ou bien
d'accroître les entrées du réseau de neurones avec les
signaux
En considérant l'aspect dynamique du système,
l'équation différentielle de la sortie y l'instant t
+ 1peut être écrite de la façon suivante :
y(t+1)=f (y(t),..., y(t-1+n),..., u(t),...,u(t-1+m))
(II-18)
Ou y (t+1) est la sortie du processus à
l'instant t+1 et f est la fonction non linéaire
régissant le
fonctionnement du processus. Cette fonction dépend des
sorties antérieures jusqu'à l'ordre n et des
entrées antérieures jusqu'à l'ordre m du
processus la sortie y(t+1) du réseau de neurones à l'instant
t +1est décrite comme suit :
y(t+1)= ??
^(y(t),...,y(t-1+n),...,u(t),...,u(t-1+m))
(II-19)
Ou ?? ^ représente la fonction d'approximation
non-linéaire de la fonction f du processus. La sortie du
réseau neurones y(t+1) dépend des sorties et entrées
antérieures du processus respectivement jusqu'aux ordres n et
m. Elle ne dépend pas des sorties antérieures du
réseau neurones. Si la sortie de l'identificateur neuronal se rapproche
de celle du processus après quelques itérations d'apprentissage,
alors nous pouvons l'utiliser comme entrée. On aura ceci :
y (t+1)=?? ^ (y(t),..., y(t-1+n),...,
u(t),..., u(t-1+m)) (II-20)
| 


