II.2.2 Fonction linéaire :
C'est l'une des fonctions d'activations les plus simples, sa
fonction est définie par [11] : F(x)=x
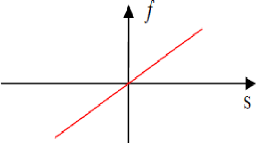
Figure. II.4. Fonction linéaire.
II.2.3 Fonction linéaire à seuil ou
multi-seuils : On peut la définir comme suit :
IX , X E [U, v]
F(X) = v ,Si X v (II.3)
U , Si X < U
II.2.4 Fonction sigmoïde :
Elle est l'équivalent continu de la fonction
linéaire. Etant continu elle est dérivable, d'autant plus que sa
dérivée est simple à calculer, (figure.
II.5) elle est définie par [11] :
??1 ??) = 1 ??2 ??~ = 1-??-??
1+??-?? 1+??-??
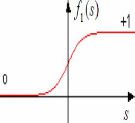

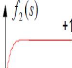
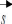

Figure. II.5. Fonction sigmoïde.
| 


