III.2. Hypothèse de la théorie des
réponses aux items
L'IRT repose sur trois hypothèses fondamentales :
l'unidimensionnalité, la monotonicité et l'indépendance
globale.
III.2.1. I VKidiPHKliRKK3lit'
La TRI postule l'unidimensionnalité de l'instrument de
mesure (le test) auquel elle est appliquée. Concrètement cela
suppose que tous les items contribuent à appréhender chez les
élèves un unique attribut: leur niveau de compétence.
Il existe différente approches qui permettent
d'évaluer la validité de cette hypothèse, parmi lesquelles
on peut citer le coefficient alpha de Cronbach ou l'analyse factorielle et
notamment l'analyse en composantes principales.
III.2.2. / 'iXCaliCDXFl lRFDll
En TRI, la validité des estimations relatives aux
caractéristiques des individus suppose que la condition dite
d'indépendance locale soit satisfaite ; condition selon laquelle, pour
un niveau d'aptitude donné, les réponses d'un sujet sont
statistiquement indépendantes, c'est-à-dire que la performance
(échec ou réussite) à chaque item n'est pas
influencée par la performance relative aux restes items.
Ainsi pour un niveau de compétence donné, la
corrélation entre les résultats des individus à deux items
quelconques doit être nulle ou, tout au moins, proche de zéro.
En termes de probabilité elle se traduit par la relation
suivante :
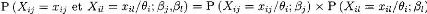
III.2.3. La monotonocité
La monotonocité concerne la fonction de réponse
aux items, elle doit être non décroissantes et monotone du trait
latent thêta, en d'autres termes, on doit avoir :
????(?????? = ??????/?? ??,????) >
0
?? ????
oil íj est un vecteur de param~tres
caractérisant l'item j.
Aussi, il est important de signaler que La taille de
l'échantillon est un facteur à prendre en compte car plus le
modèle est complexe, plus il nécessitera de sujets. Avec des
échantillons de 100 à 200 personnes, le modèle de Rasch
est le
seul choix possible. Le modèle à deux
paramètres demandera au moins trois fois plus de sujets, et le
modèle à trois paramètres dix fois plus (Jones, 1992).
Dans notre cas, nous avons des échantillons de 2361
élèves en 2005 et 2553 élèves en 2011.
| 


