Commande vectorielle à flux rotorique orienté de la machine asynchrone:simulation et expérimentation

RAPPORT DE PROJET TUTORE

COMMANDE VECTORIELLE A FLUX ROTORIQUE
ORIENTE DE LA MACHINE ASYNCHRONE :
SIMULATION ET EXPERIMENTATION

Par
Danic TOFFESSI YAPTA
Master 2 SEE -- Energie Electrique
Sous l'enca drement de :
Pr. Abderre%ak REZZOUG
et
Dr. Thierry LUBIN

ANNEE ACADEMIQUE
2009- 2010

Remerciements.

REMERCIEMENTS

> Je remercie tous les enseignants du cycle de Master «Systèmes Embarqués et Energie » de la faculté des sciences de l'Université Henri Poincaré, Nancy 1 et particulièrement ceux de la spécialité « Energie Electrique ».

> Je remercie très particulièrement Monsieur Abderrezak REZZOUG, Professeur à l'UHP, chercheur au GREEN et co-encadreur de ce projet, d'avoir accepté de m'encadrer et de m'avoir suivi et aidé à mener à bien ce projet à travers sa rigueur scientifique, ses encouragements, son attention qui a été toute particulière et surtout son cours sur les régimes dynamiques et commande des machines qui m'a passionné et poussé vers ce projet.

> Je remercie aussi et très particulièrement Monsieur Thierry LUBIN, Maître de conférences à l'UHP, chercheur au GREEN et co-encadreur de ce projet, d'avoir accepté de m'encadrer, de m'avoir soutenu et de m'avoir vraiment beaucoup aidé ; surtout dans la partie expérimentale : compréhension des programmes et réalisation pratique de la commande vectorielle.

> Je remercie le GREEN (Laboratoire de Recherche en Electronique et Electrotechnique de Nancy) de m'avoir permis de réaliser ce projet dans leurs locaux de l'UHP.

Rapport de projet réalisé, ré digé et présenté par Danic TOFFESSI YAPTA Master 2 SEE- Energie Electrique, UHP - Nancy 1, 2009/2010

SOMMA1RE

REMERC1EMENTS i

SOMMA1RE................................ ................................ ................................ ............. ii
RESUME................................ ................................ ................................ ................. iii
L1STEDES NOTAT1ONS ................................ ................................ .......................... iv

1NTRODUCT1ON GENERALE 1

Chapitre 1 : MODEL1SAT1ON DE LA MACH1NE ASYNCHRONE EN VUE DE LA

COMMANDE................................ ................................ ................................ .......... 2

1- Modélisation mathematique de la machine..........................................................2

1.1- Equations de la machine asynchrone en regime quelconque...................................... 2

1.2- Modèle diphasé de la machine ................................................................................. 3

1.2.1- Transformation de Clarke ou de Concordia.................................................................... 3

1.2.3- Transformation de Park................................................................................................. 4

11- Modele de la machine dans un repere de Park....................................................5

11.1- Equations de la machine asynchrone en regime dynamique...................................... 5

11.2- Choix de l'orientation du repere (d ,q ) de Park ..................................................... 6

111- Comman de vectorielle de la machine asynchrone..............................................7 111.1- Choix de la strategie de comman de ........................................................................ 8 111.2- Choix de l'orientation du flux ................................................................................ 8

111.3- Calcul de l'angle è_s des transformations ................................................................ 9

111.4- Choix du mode d'alimentation .............................................................................10
111.5- Synthese du modele final .......................................................................................11
111.6- Decouplage des comman des des axes d et q ........................... 12

111.7- Regulation 14

111.7.1- Regulation des courants 14

111.7.2- Regulation et asservissement de la vitesse 14

Chapitre 2 : S1MULAT1ON DE LA COMMANDE VECTOR1ELLE A FLUX ROTOR1QUE OR1ENTE DANS L'ENV1RONNEMENT MATLAB-S1MUL1NK 16

1- Conception des différents blocs dans Simulink.................................................... 16

1.1- Blocs de transformation 16

1.2- Bloc Machine Asynchrone 17

1.3- Bloc On duleur 21

1.4- Bloc Orientation du flux rotorique 21

1.5- Bloc Autopilotage 21

1.6- Bloc Régulateur 21

1.7- Bloc Découplage (par compensation) 21

Rapport de projet realise, redige et presente par Danic TOFFESS1 YAPTA Master 2 SEE- Energie Electrique, UHP - Nancy 1, 2009/2010

II- Simulation du demarrage direct de la machine asynchrone................................22

III- Synthése des régulateurs (de type PI) ...............................................................23 III.1- Modélisation de l'on duleur a MLI......................................................................... 23 III.2- Correcteurs de courant......................................................................................... 23 III.3- Correcteur de vitesse............................................................................................ 24

IV- Simulation de la comman de vectorielle in directe ................ 25

IV.1- Calcul des valeurs nominales des references 25

IV.1.1- Valeur nominale I_sdn du courant d'axe d 25

IV.1.2- Valeur nominale I_sqn du courant d'axe q 26

IV.1.3- Valeur nominale C/_n de la vitesse 26

IV.2- Illustration du decouplage de la comman de des axes d et q 26

IV.3- Comman de vectorielle en mode non decouplee (sans compensation) 26

IV.4- Comman de vectorielle en mode decouplee (avec compensation) 29

Chapitre 3 : EXPERIMENTATION DE LA COMMANDE VECTORIELLE A FLUX ROTORIQUE ORIENTE DE LA MACHINE ASYNCHRONE 34

I- Principe de la mise en oeuvre ............................................................................34

I.1- Schema de principe................................................................................................. 34

I.2- Description des differents blocs 34

II- Pilotage de l'ensemble du systéme ....................................................................35

II.1- Programmation du DSP ......................................................................................... 35

II.2- Discrétisation des correcteurs 36

III- Résultats expérimentaux ..................................................................................37

III.1- Echelon de courant Is d.......................................................................................... 38

III.2- Echelon de vitesse de 50 ra d/s 39

III.3- Echelon de vitesse de 200 ra d/s 40

III.4- Inversion de vitesse de 100 ra d/s a -100 ra d/s........................................................ 41
III.5- Echelon de couple resistant 42

CONCLUSION GENERALE ................................ ................................ ..................... 44

REFERENCES BIBLIOGRAPHIQUES 45

ANNEXES................................ ................................ ................................ 47

ANNEXE 1 : IENTIFICATION DES PARAMETRES DE LA MAS 48

ANNEXE 2 : EXTRAITS DE PROGRAMMES ET FONCTIONS 53

Rapport de projet realise, rédigé et présenté par Danic TOFFESSI YAPTA Master 2 SEE- Energie Electrique, UHP - Nancy 1, 2009/2010

Résumé.

RESUME

Ce projet semestriel intitulé « Commande vectorielle à flux rotorique orienté de la machine asynchrone : Etude, simulation et expérimentation dans l'environnement Matlab-Simulink/dsPACE » s'inscrit principalement dans un cadre d'apprentissage et de formation, avec tous les aspects techniques et pédagogiques qu'il porte.

Il s'agit de comprendre le principe et les objectifs de la commande vectorielle, de la conception à la mise en oeuvre effective et pratique à travers la modélisation, la simulation et l'expérimentation.

Partant des équations de fonctionnement de la machine asynchrone, un premier modèle a été élaboré en tenant compte de certaines hypothèses simplificatrices ; modèle décrivant le fonctionnement de la MAS et permettant d'étudier le démarrage direct, avec association du repère de Park au champ tournant.

La stratégie de commande envisagée est celle de la commande indirecte de flux (boucle ouverte) qui intègre les boucles de régulation des courants Isd et Isq ainsi que de la vitesse ; avec une alimentation en tension et contrôlée en courant. Les différents régulateurs ayant été dimensionnés à partir des paramètres de la machine qui ont été identifiés au cours de ce projet.

Le modèle de la machine exploité dans ce projet a été élaboré en fonction des seuls paramètres qui décrivent complètement son fonctionnement et qui sont par ailleurs accessibles et mesurables ; permettant ainsi d'étendre ce travail (principalement la partie simulation) à toutes les MAS indépendamment de la construction du rotor.

Ensuite, la simulation et enfin, l'expérimentation ont ensuite été effectuées en régime dynamique dans plusieurs conditions et les résultats sont donnés dans les chapitres respectifs.

Rapport de projet réalisé, ré digé et présenté par Danic TOFFESSI YAPTA Master 2 SEE- Energie Electrique, UHP - Nancy 1, 2009/2010

Liste des notations.

LISTE DES NOTATIONS

R_s : Résistance d'une phase stator R_r : Résistance d'une phase rotor

k₂ : Résistance d'une phase rotor ramenée au stator L_s : Inductance cyclique d'une phase stator

L_r : Inductance cyclique d'une phase rotor

M : Inductance mutuelle cyclique entre stator et rotor L_f : Inductance des fuites totalisées au stator

ó = 1 - L sL r : Coefficient de dispersion de Blondel



2

M

ô_s : Constante de temps statorique

ô_r : Constante de temps rotorique

I) : Nombre de paires de pôles

J : Moment d'inertie de l'ensemble ramenée à l'arbre du moteur

è_s : Angle électrique entre stator et axe d

è_r : Angle électrique entre stator et rotor è : Angle électrique entre axe d et le rotor ù_s : Pulsation des courants statoriques

ù_r : Pulsation des courants rotoriques

ù : Pulsation mécanique du rotor Ù : Vitesse mécanique du rotor Cem : Couple électromagnétique

C_r : Couple résistant

f : Coefficient des frottements visqueux I_s : Courant statorique

I_r : Courant rotorique

Isd : Courant statorique d'axe d

Isq : Courant statorique d'axe q

Ird : Courant rotorique d'axe d

Irq : Courant rotorique d'axe q

Imr : Courant magnétisant rotorique Imd : Courant magnétisant d'axe d Imq : Courant magnétisant d'axe q ø_s : Flux statorique

ø_r : Flux rotorique

øsd : Flux statorique d'axe d

øsq : Flux statorique d'axe q

ørd : Flux rotorique d'axe d

ørq : Flux rotorique d'axe q

V_s : Tension simple statorique

V_sd : Tension simple statorique d'axe d
V_sq : Tension simple statorique d'axe q

Rapport de projet réalisé, ré digé et présenté par Danic TOFFESSI YAPTA Master 2 SEE- Energie Electrique, UHP - Nancy 1, 2009/2010

Introduction générale.

INTRODUCTION GENERALE

Les machines à courant continu (MCC) occupent de nos jours de moins en moins le marché de la variation de vitesse. Elles sont beaucoup utilisées en traction électrique et en robotique car elles permettent un contrôle séparé du flux et du couple : la production du couple et la création du flux sont indépendantes. Mais cette machine sensible nécessite un entretien relativement lourd et possède un couple volumique inférieur et un prix supérieur aux autres technologies de machines. Ainsi, elle a beaucoup tendance à être remplacée par des machines à courant alternatif : machines synchrones (MS) et asynchrones (MAS) ; et dans ces conditions, la machine nécessite un convertisseur et un calculateur biens adaptés (onduleur et microcontrôleur).

Avec l'apparition de l'électronique de puissance et pour la machine asynchrone, parti de la cascade hyposynchrone qui permettait de fonctionner à vitesse variable et fréquence fixe, on est arrivé à un fonctionnement à fréquence variable grâce à la commande scalaire (à flux constant) qui reste basé sur le régime permanent et ne permet pas le contrôle des régimes dynamiques.

L'évolution de cette discipline a permis de développer des interrupteurs de puissance capables de commuter à des courants, tensions et fréquences très élevés (de l'ordre de 100kHz) ainsi que des calculateurs très puissants et rapides ; notamment le DSP (Digital Signal Processor) qui, associé à un onduleur, permet aujourd'hui de contrôler les régimes dynamiques des machines à courant alternatif à travers la commande vectorielle.

Cette maîtrise indépendante du couple et du flux rend possible l'utilisation de ces machines sur des marchés traditionnellement occupés par les machines à courant continu. Ce qui permet d'une part en traction, de minimiser les ondulations de couple et de fournir un couple de démarrage important. En robotique, la machine possède une dynamique élevée et peut fournir un couple de maintien à vitesse nulle (positionnement).

Ce projet semestriel s'inscrit donc principalement dans un cadre d'apprentissage et de formation, avec tous les aspects techniques et pédagogiques qu'il porte.

Chapitre 1 : MODELISATION DE LA MACHINE ASYNCHRONE EN VUE DE LA COMMANDE

Introduction

La commande vectorielle de la machine asynchrone est principalement basée sur le régime transitoire par opposition à la commande scalaire qui elle, est basée sur le régime permanent. Il est donc nécessaire et même indispensable de lui donner un modèle réaliste (équations mathématiques) permettant son étude en régimes transitoires.

Ce modèle qui doit se rapprocher au mieux de la réalité, est obtenu à partir des équations des tensions (stator et rotor) de la machine, combinées aux équations de flux et exprimées dans un repère diphasé quelconque de la machine.

Hypotheses de travail

L'étude de cette machine traduit les lois de l'électromagnétisme dans le contexte habituel d'hypothèses simplificatrices :

- machine en régime linéaire (saturation négligée) ;

- entrefer constant ;

- répartition spatiale sinusoïdale des forces magnétomotrices dans l'entrefer ;

- effets d'encoches négligés ;

- pertes fer négligées ;

- effet de peau négligé ;

- inexistence de la composante homopolaire car l'alimentation de la machine est faite avec neutre non sorti (couplage étoile).

I- Modelisation mathematique de la machine

I.1- Equations de la machine asynchrone en regime quelconque

D'un point de vue électrique, les enroulements statoriques et rotoriques de la machine asynchrone dans l'espace, peuvent être représentées comme sur la figure ci-dessous :



Figure 1-1 : Representation des enroulements de la machine [12]

Sur cette figure, è est l'angle entre la phase (a) du stator et la phase (A) du rotor dont les enroulements sont en court circuit.

La loi de Faraday permet d'écrire :

v Ri d ?

= + (1.1)

(1.2)

dt

Ce qui sous forme matricielle généralisée, donne :

· Au stator d

[ _s ] s [ _s ]

v = R I + ?

[ _s ]

dt

· Au rotor d

[ _r ] r [ _r ]

v = 0 = R I + ? (1.3)

[ _r ]

dt

~ v sa ~

~

Avec : [ v_s]

= ~ v ; [ ]

v

~ sb ~ r

~ ~

v

sc ~

~ v ra ~

~

= ~ v ; [ ]

I

~ rb ~ s

~ ~

v

rc ~

~ I sa ~



~

= ~ I ; [ ]

I

~ sb ~ r

~ ~ I ~

sc ~

~ I ra ~

~ ~ ~ [ ] [ ][ ] [ ][ ]

? = L I L I

+

s ss s sr r

= I et

~ rb ~ ~ ~ [ ] [ ][ ] [ ][ ]

? = L I L I

+

r rr r sr s

~ ~

Irc ~

Sans entrer dans les détails, le flux pour chaque phase est composé de son flux propre et du flux dû aux courants de toutes les autres phases. [ L_ss ] , [ _Lrr ] et [ L_sr ] étant respectivement

les matrices inductances propres (stator et rotor) et inductances mutuelles stotor-rotor.

1.2- Modele diphase de la machine

D'après le théorème de Blondel, deux enroulements en quadrature suffisent pour créer un champ tournant. Donc le champ tournant crée par un système d'enroulements triphasées (trois bobines) équilibrées peut également être crée par le système diphasé (deux enroulements en quadrature) équivalent.

1.2.1- Transformation de Clarke ou de Concordia

Passage du systeme triphase fixe au systeme diphase fixe

Les transformations de Clarke et de Concordia permettent (l'une ou l'autre) de passer d'un repère à trois axes équilibrés (triphasé) abc à un repère à deux axes en quadrature (diphasé) áâ . Ce qui est très intéressant puisque l'objectif de la commande vectorielle est de parvenir à commander séparément les deux grandeurs flux et couple qui seront chacune, associée à un axe.

L'objectif de toute commande de machine étant le transfert maximum de puissance (entre la machine et sa charge), nous choisissons pour la suite la transformation de Concordia qui conserve la puissance et non les amplitudes par rapport à celle de Clarke qui ne conserve que les amplitudes et pas la puissance. Cette transformation se fait en appliquant au système triphasé X , la matrice T_{3 2} de Concordia comme suit :

1

=



2



-

-

2



2



3

2

3

0

T3 2

[

x_a



T3 2

x_á

1 ~ i

xb

[

x_â

x_c

1 ~

~

li

soit [ x_áâ ] = T3 ₂ [ _xabc ] ; avec

(1.4)

3 1

1

2

1 ~ ~ ~ ~ ~



Figure 1-2 : Illustration du passage de abc a áâ [¹⁴]

I.2.3- Transformation de Park

Passage du repere fixe ( á , â) au repere tournant (d , q )

Toujours dans le but de rendre compte au mieux de la réalité, il est nécessaire de travailler dans un repère tournant, puisque le rotor de la machine est en mouvement.

Grâce à la transformation de Park qui n'est rien d'autre qu'une rotation d'angle è (angle
électrique correspondant à la position choisie pour la transformation), il est possible de passer
du repère fixe (á ,â ) à un repère tournant (d , q ) dit de Park, qui peut ensuite être associé

soit au stator, rotor ou champ tournant.

La transformation se fait ainsi en appliquant au système diphasé X , la matrice de rotation

R (è) telle que :

)

x_á

x d

1

1

1

R (è



1 1

_1

x_â

x_q

[

[

soit [ x_dq ] = R ( è ) [ x _áâ ] ; avec ~~

~ cos è sin è ~

R( )

è = (1.5)

~~ - sin cos

è è



Figure 1-3 : Illustration de la transformation de Park (de áâ a dq ) [12]

Le système triphasé X dans le repère ( a , b , c ) peut également et simplement être représenté par son équivalent dans le repère (d , q ) de Park par application de la matrice P(è) de Park telle que :

(1.7)

)

x_a



P(è

x d

~ ~ ~

xb

[

x_q

x_c

[

1 ~

~

LI

soit [ x _dq ] = P(è)[ x_abc ] ;

~ 2 ð 2 ð

cos ~ - ~ ~



cos ~~ ~~ ~ + ~

~ è è cos ~~ è ~~ ~

2 3 3

avec P ( è ) = ~ ~ (1.6)

3 ~ ~ - 2 ð ~ ~ ~

- - è ~~ - ~ + 2 ð

sin è sin

~ ~~ sin ~~ è ~~ ~

~ 3 3 ~

Dans la suite, nous utiliserons cette transformation directe qui rend les différentes grandeurs constantes.



( )

ù ã

t +

~ + - 2 ð ~

~~ ù ã ~~

3

t

~ + + 2 ð ~ ~~ ù ã

t ~~

3

v _sa= V

v sb V

v _sc= V

cos

cos

2. cos

2.

2.

L

Pour un système de tensions statoriques _vabc triphasé équilibré telle que :

La transformation est :[v _dq ] = P(è)[ _vabc ] et le développement du calcul fournit :

V_sd = V 3 cosã et V_sq = -V 3 sinã (1.8)





II- Modele de la machine dans un repere de Park

II.1- Equations de la machine asynchrone en régime dynamique

Ces différentes transformations conduisent finalement au modèle mathématique général dans un repère de Park, utilisé pour la machine asynchrone en régime transitoire. Ce modèle est décrit par les équations ci-dessous :

Equation des tensions Equation des flux

Equation des tensions

Equation des flux

· Stator

· Stator
· Stator

· Stator

d ø

sd

è

+

dt

s sq

ø

Vsd

Isd

R_s

dø

èø s sd

sq

+ +

R_sI _sq

Vsq

dt

L

· Rotor

dø

rd

0

-

+

èør rq

I rd

Vrq

R_r



ø sd = L sI _sd + MI _rd

(1.11)

sq s

· Rotor

ø rd = LrI _rd + MIsd

(1.12)

rq r

~ ~ ~

L I _rq + MIsq

ø

~ ~ ~

L I _sq + MIrq

ø

(1.9)



dt

dø

èør rd

rq

+ +

RrIrq

0

L

Vrq

dt

(1.10)

Couple électromagnétique

Le couple électromagnétique s'exprime par différentes expressions [5] dont celle qui nous intéressera est :

Cem = t M (Ird Isq - IrqIsd)=t (M Isq ^ø -Isd ø rq) Lr

(1.13)

11.2- Choix de l'orientation du repere (d , q ) de Park

Le repère tournant (d , q ) de Park peut être lié :

- soit au stator ( è^~_s = 0 et è~ r = ù_r) pour l'étude des grandeurs rotoriques.[13]

- soit au rotor ( è~ s = ù_s et è~ r = 0 ) pour l'étude des grandeurs statoriques.[13]

- soit au champ tournant ( è~ s = ù_s et è~ r = ù_r) pour la commande [13]

En choisissant d'associer le repère (d , q ) de Park au champ tournant ( è~ s = ù_s et è~ r = ù_r) car les grandeurs transformées dans les axes d et q deviennent constantes, indépendantes du temps et donc faciles à réguler [2]. On obtient les équations électriques ci-dessous :



+

dø

sd

dt

Vsd

I sd

R_s

+

MIrd

ùø s sd

I _sq + MIrq

Vsq

sq

+ +

dø

øsd

L_s

R_sI _sq

dt

øsq

L_s

I _sd

avec

(1.14)

+

dø

L_r

+

MIsd

ø rd

I rd

rd

0

ù

~

~~ ~ ~ ~

r ø rq

I rd

Vrq

R_r

dt

I _rq + MIsq

rq

L_r

Lø

L

dø

ù

rq

+ +

0

dt

RrIrq

r ø rd

Vrq

ssq

ø

ù

La combinaison de ces équations conduit à plusieurs configurations sous forme d'équations d'état, selon les besoins. La configuration qui sera utilisée dans ce projet est donnée ci-dessous :



sd

M2 L2Rs

= ~ I ~

dt M² L_r +L² Ls sd

R_rM

L2 L s - M²L_r

+

+ ù_s

I_sq

r

Mù

1

2

ø rd

Vsd

+

+

2

M

ørq

L_s

L_rL _s-M

L_r

M R L R

2 2

~ + ~

r r s

~ I ~

2 2 sq

~ M L L L

+

r r s ~

ù_s

~

~

~

dI sq

dt

I sd

Isd

dø

rd MRr

dt L_r

r

MR

dø

rq

L

I_sq

dt

L_r

+

R_r

ù

L_r

r ø rq

ørd

ù

R_r

L_r

r ø rd

ø rq

Mù

1

R_rM

r

^Vsq

2

2

ørq

ø rd

+

+

L2 L s - M²L_r

M

L_s

L_rL _s-M

L_r

(1.15)

Avec ce modèle d'état qui représente la machine asynchrone réelle, l'étude du démarrage ainsi que d'autres régimes transitoires (échelon de couple, court circuit des

phases,...) peut être faite par simulation et ce, de façon très aisée. Une illustration sera faite dans la partie Simulation (chapitre 2) de ce projet.

III- Comman de vectorielle de la machine asynchrone

Le contrôle vectoriel de la machine asynchrone construite ci haut (1.15), consiste principalement à commander en régime dynamique et séparément (de façon découplée) le flux et le couple comme c'est le cas (naturellement) pour une machine à courant continu (excepté de type série).

Le schéma général de principe est le suivant :



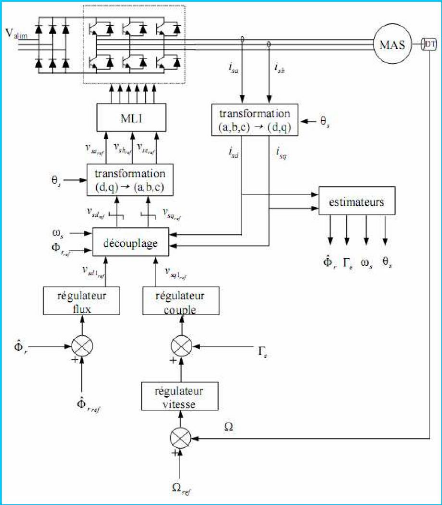
Figure 1-4 : Schéma de principe d~une comman de vectorielle ( directe) [¹²]

111.1- Choix de la stratégie de comman de

Le contrôle vectoriel consiste donc à choisir un système d'axe (d ,q ), de façon à régler le flux par une composante du courant ( I_sd ) et le couple par l'autre composante ( I_sq ).

Ainsi, on peut construire une loi de commande assurant le découplage du couple et du flux permettant d'obtenir des fonctionnements comparables à ceux de la MCC (excepté de type série).

Cette régulation de flux statorique ou rotorique (orienté suivant l'un des axes d et q) peut être soit directe soit indirecte.[4]

· Contrôle directe : le flux est régulé par une contre-réaction. Il doit donc être mesuré ou estimé.

· contrôle indirect : le flux n'est ni mesuré ni reconstruit. Il est fixé en boucle ouverte. Ainsi, les tensions ou courants assurant l'orientation du flux et le découplage sont évalués à partir d'un modèle de la machine en régime transitoire.

Nous adopterons dans ce projet une stratégie de commande indirecte par orientation du flux rotorique avec capteur de position ou de vitesse au rotor, nécessaire pour effectuer les changements de coordonnées. Elle est plus simple que la commande directe mais les résultats obtenus sont de performances plus faibles.[5]

111.2- Choix de l'orientation du flux

La suite du raisonnement consiste à fixer l'orientation du flux. Trois possibilités se présentent :

- Flux statorique : ø sd = ø _s et øsq = 0 (1.16)

- Flux d'entrefer : ø ed = øe øeq = 0 (1.17)

- Flux rotorique : ø rd = ø _r et ørq = 0 (1.18)

L'orientation du flux statorique et du flux d'entrefer ne donne pas de bonnes performances par rapport à l'orientation du flux rotorique qui permet d'obtenir un couple important tout en nécessitant une adaptation des paramètres rotorique (qui varient avec la température et la fréquence)[4]. L'orientation du flux rotorique permet aussi d'éliminer l'influence des réactances des fuites rotorique et statorique et est ainsi la plus utilisée.

Nous choisissons donc d'orienter le flux rotorique suivant l'axe d du repère (d , q ) de Park. D'où l'appellation classique « Commande vectorielle à flux rotorique orienté. » (en réalité, c'est l'axe d qui est orienté sur le flux rotorique). Ainsi, les conséquences (ø rd = ø r

et ørq = 0 ) sont injectées dans les équations du modèle pour obtenir les lois de commande et d'autopilotage ci-dessous :

· Loi de commande par orientation de flux rotorique

Elle est obtenue par la dernière équation du système d'état (1.15) :

ùr = I sq ôrø rd		(1.19)

0 = MR - ù ø soit :

^r I

sq r rdLr


· Loi d'autopilotage

Il s'agit simplement de la loi de fonctionnement de la machine asynchrone, mais en tenant compte de la loi d'orientation ci-dessus.

Nous avons donc : ù_s = ù_r + ù . (1.20)

Et avec ùr = I^sqet ù = 1Ù , nous obtenons : ôrø rd

Isq ùs = +1Ù ô r ø rd

(1.21)

111.3- Calcul de l'angle ès des transformations

Pour obtenir l'orientation choisie, il faut calculer la pulsation statorique ù_s à intégrer pour obtenir l'angle è_s nécessaire aux transformations de coordonnées.

On obtient donc à partir du calcul précédent (1.22), l'angle de transformation :

= Jùsdt =J(

^sq +1Ù )dt

ô r ørd

è_s

(1.22)

On peut ainsi à partir de la mesure de la vitesse (angulaire) mécanique, estimer la pulsation statorique et par conséquent l'angle des transformations.

Le couple électromagnétique devient avec ø r = MImr :

M ²

M ( ) ( mr sq ) ( ) _s [ mr sq ]

I = p I I p 1 L I I

ø = - ó

sq rd

L_r

C _em= p

L_r

(1.23)

Le courant magnétisent I_mr étant à la constante de temps rotorique près, l'image du courant _Isd . Le courant _Isd permettra de fixer le flux ø_r et le courant _Isq servira à piloter le

couple électromagnétique.

Un schéma de principe d'une commande vectorielle indirecte à flux orienté, intégrant les

différents blocs de calcul des lois est le suivant :



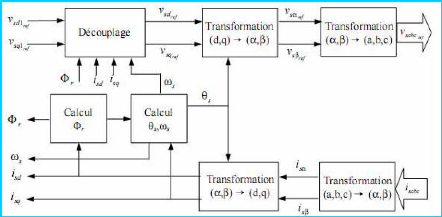
Figure 1-5 : Schéma de principe d'une comman de vectorielle in directe a orientation de flux [12]

111.4- Choix du mode d'alimentation

Pour ce type de commande, l'alimentation de la machine est faite par un onduleur de courant ou de tension selon les besoins.

· Alimentation en courant Pour une alimentation en courant, les variables de commande sont _Isd ^et _Isq . Mais la

source de courant est lourde et chère à cause des inductances de lissage. Ce mode d'alimentation est beaucoup plus réservé aux applications de très fortes puissances où la forme du courant est particulièrement prise en compte (pour réduire les ondulations de couple).

· Alimentation en tension Dans ce cas, les variables de commande sont _Vsd et V_sq . Les onduleurs de tension qui

ne nécessitent pas d'inductance lourde et coûteuse indispensable pour réaliser une source de courant, sont beaucoup préférés et utilisés en traction électrique (TGV transmanche, voiture électrique,...) [5].

Nous choisissons donc pour la machine une alimentation en tension et contrôlée en courant. De tous les modèles courants, nous choisissons le modèle ayant pour:

- variables d'état : Isd , _Isq , _ørd ^et ørq .

- variables de commande : Vsd et V_sq .

Ce modèle qui est utilisé pour orienter le flux rotorique ø_r [5] est celui décrit par le système d'équations d'état (1.15) précédent.

111.5- Synthese du modele final

En injectant les expressions de l'orientation du flux rotorique (ø rd = ø _r et ørq = 0 ) dans les équations des tensions (1.14), on obtient :



RrIrq

0

dø

r

MIrdd

Isd

I MI

+

sq rq

L_r

I rd

MIsdd

L_r

Irq q+#177;MIsqq

Vsd

^Vsq

R_s

0

Isd

R_r

ù

ù

s sq

ø

øsd

øsq

ør

0

RsIsq

s sd

ø

~

~

L

+

dø

sd

dø

sq

+ +

dt

+

dt

+

ù

r ør

~

~~

L

dt

I rd

avec

L_s

L_s

(1.24)

Et le couple électromagnétique : ( sq rd )

C = p I ø

^em L r

M

(1.25)

Le flux rotorique peutêtree obtenu par la relation :ø _rr = MI_mr . (1.26)On définit ainsi le courant magnétisant I mr,== et on obtient de la troisième équation duu

(1.22), combinée à celle des flux :

d

ø M 1 dI 1 - 1

rd mr

= I ø

sd - =

r ? I I

sd

dt

mr

ô r ôr

dt ô ô

devient : pI _mr ô r = I sd - I _mr .

1

Ce qui donne : sd

I = I

^mr 1

+ pô_r

r r



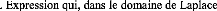
(1.27)

Relation montrant que les deux grandeursI_mr. et I_sd sontégales,, enrégimee permanent.

Apres combinaison deséquationss du (1.22), leséquationss des tensions statoriquesen n d et qs'écriventt :



R_s

Isd

+

dø/

dtt

MM

rr

+

Lrr

MLr) 2 dI sd M ù _s- _Lr )I

sq

~ _-M² ~
~ ~

~ L r ~

R_s

I _sq + L_s

(1.28)

~

~~ ~ ~ ~

Vsd

^Vsq

L

+

MM

Lrr

~ -M 2 ~

~ L I ~

s sd

~ L r ~

:

dt

+ ù_s

dIsq

1

dans les

Dans le domaine de Laplace, en remplaçanø _rr = MImrr , ave sd

I = I

^1
1

mr d++pôr,

équations ci-dessus, on obtient :



2

M

_M2

+L s - ^M Isd -ùL s - ML:1I

L_r^sq

~ -M 2 ~

~ L I ~

s sd

~ L r ~

:

~

~~ ~ ~ ~

Vsd

Isd

R_s

L

RsIsq

^Vsq

22

MM

pImrr

22

(1.29)

MM

mrr

LL

Lrr

L_r

)pI

sq

~ ~
~

+

L_s

+ ù_s

On peut constateràa partir de ceséquationss que lesystèmee des deux axes est ^fortementcouplée : chacune des composantes (entrées)V_sdd et V_sq de la tension influenceàa la fois les
courants (sorties) I_sd etI_sqq . Pour contourner ceproblèmee et pouvoircontrôlerr le flux

. Expression qui, dans le domaine de Laplace

indépendamment du couple, nous allons transformer ce système multi variable (deux entrées et deux sorties couplées) en deux systèmes mono variables (une entrée, une sortie).

111.6- Décou p l age des comman des des axes d et q

Pour découpler l'évolution des courants _Isd ^et _Isq , nous définissons deux nouvelles entrées notées Vsd 1 et Vsq 1 dont les équations correspondantes font appel respectivement à Isd et _Isq . Plusieurs techniques permettent ainsi le découplage des axes d et q :

· découplage par utilisation d'un régulateur [12] ;

· découplage par retour d'état [12] ;

Ici il s'agit de déterminer une commande par retour d'état qui découple le système de façon q'une sortie ne dépende que d'une seule entrée (correspondante).

· découplage par compensation [11], [12]

Nous nous intéresserons par la suite à cette technique de découplage qui parait la plus simple car elle consiste à ajouter sur chacun des axes des termes de découplages respectifs, mais de signes opposés.

_M2 _M2 } _M2

En posant : V sd 1 = RsI _sd + L s jpI _sd et e _sd = +ù_sL_s pIm _r ainsi que

L_r L ^sq r Lr

_M2 _M2 _M2

V sq 1 = RsI _sq + L s }JI_m et e _sq = -ù_s L s- y L ^L

sd y pI _mr , on obtient en

Lr r r

simplifiant l'écriture le système ci dessous:

= ( R _s + óL_s p ) I sd - ù_s ó LsI _sq +(1- ó

( R L p I

+ ó ) + ù ó + -

(

s s sq s s sd

L I ó

1

)L s pImr V _sd1 + esd

)LI V e

= +

s mr sq 1 sq

(1.30)

~ ~~

~~

Vsd

Vsq

En admettant que le courant magnétisent (flux) varie très peu par rapport aux courants Isd ^et _Isq (ce qui est vérifié en simulation et en expérimentation) [9], on se réduit à :

esd =-ù_s óL_s I _sq

e = + ù ó + -

( )

1

sq s s sd

L I ó L _s

~ ~~
~~

I

mr

(1.31)

On peut ainsi avec les fonctions de transfert :

1

( R _s + óL _sp)

et I sq = Isq

= V V e ( R L p)

+ + ó

sq sq 1 sq s s

Isd Isd

Vsd Vsd 1 + esd

1

(1.32)

construire les schémas blocs ci-dessous, illustrant le couplage des commandes en d et q .

Vsd 1		Vsd

Vsq 1		Vsq

Figure 1-6 : Illustration du couplage des comman des des axes d et q Modele de la MAS dans le repere (d , q ) de Park

Les dynamiques des courants I_sd et _Isq sont du premier ordre ; ce qui simplifie la

synthèse des correcteurs. En plus, le gain et la constante de temps sont indépendants de la résistance rotorique ; ce qui représente un avantage pour la robustesse du système.

Par contre les tensions e_sd et e_sq varient, avec la résistance rotorique à travers le courant

magnétisant.

La compensation consiste à ajouter des tensions identiques mais de signes opposés à la sortie des régulateurs de courant de manière à annuler l'influence d'un axe ( I_sd ) sur l'autre

( I_sq ) et vice-versa [9]. Le découplage est donc illustré ci-dessous :



Modèle de la MAS

Découplage dans le repère (d ,q ) de Park

Vsd 1		Vsd	Vsq 1
Vsq



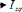
Figure 1-7 : Schéma de découplage par compensation



MAS avec découplage des axes d et q

111.7- Régulation

Le contrôle des grandeurs flux et couple de la machine passe par l'asservissement de la dynamique des courants statoriques _Isd ^et I_sq à l'aide des tensions de commande _Vsd et

V_sq qui leur sont liées ainsi qu'à la pulsationco_s .

111.7.1- Régulation des courants

A partir de la figure précédente, on aboutit à un schéma bloc simple pour chacun des deux axes : Ce qui correspond à la boucle de régulation de chacun des courants _Isd ^et _Isq .



Figure 1-8 : Boucles de régulation des courants I_sd et I_sq

111.7.2- Régulation et asservissement de la vitesse

La chaîne de contrôle de la vitesse peut être représentée par le schéma fonctionnel ci-dessous :



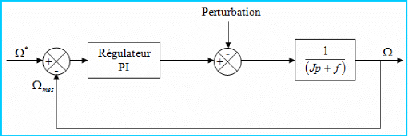
Figure 1-9 : Contrôle de la vitesse mécanique

Ces régulateurs (de courant et de vitesse) qui sont simplement des correcteurs PI (Proportionnel et Intégral) seront synthétisés en continu et en discret dans les chapitres respectifs de simulation et d'expérimentation.

Le choix des régulateurs PI est ici justifié par sa simplicité de mise en oeuvre. Ce qui simplifie considérablement et avantageusement le problème car les régulateurs PID (Proportionnel, Intégral et Dérivé) bien que permettant d'anticiper et d'accélérer la régulation, ne conviennent pas car sont très sensibles aux bruits et donc amplifient beaucoup ceux-ci [9].

Tous les détails de calcul de ces correcteurs en continu et en discret seront faites dans les chapitres correspondants.

On aboutit donc à un schéma de commande vectorielle indirecte avec régulation des courants sur les deux axes correspondant respectivement au flux et au couple de la machine. La commande est dite indirecte (commande en boucle ouverte) car il n'y a pas de boucle directe de régulation de flux.

Ce schéma peut être par la suite complété par une boucle de régulation de position ou de vitesse comme nous le verrons par la suite.



Figure 1-10 : Schéma de la comman de vectorielle in directe avec régulation de courant [¹4]

Conclusion

Le travail de modélisation effectué jusqu'ici a permis de donner à la machine asynchrone un modèle global (qui peut être adapté selon les besoins) à partir des différentes équations de fonctionnement. Ce modèle permettant déjà l'étude de la machine en régime transitoire.

Pour la commande vectorielle, tous les éléments fondamentaux et nécessaires ont été choisis et définis ainsi que les boucles de régulation. La suite (chapitre 2) va consister en la simulation d'abord du démarrage et ensuite de la commande vectorielle. Cette dernière se faisant en passant par la synthèse des différents régulateurs.

Chapitre 2 : SIMULATION DE LA COMMANDE VECTORIELLE A FLUX ROTORIQUE ORIENTE DE LA MACHINE ASYNCHRONE DANS L'ENVIRONNEMENT MATLAB/SIMULINK

Introduction

La mise en oeuvre de tout système de commande de dispositifs électromécaniques, commençant toujours par une modélisation suivie du dimensionnement de différents paramètres, passe avant la réalisation, par une phase capitale dite « de simulation » qui permet d'avoir une image du comportement réel du système à mettre en oeuvre. Ainsi, Il est facile d'en prévoir les conditions de fonctionnement. Le chapitre précédent a été consacré à la modélisation de la machine asynchrone et à la définition de tous les éléments nécessaires à sa commande vectorielle indirecte.

Dans cette partie, il s'agira essentiellement de concevoir dans l'outil Matlab/Simulink, les différents blocs et les assembler ensuite, pour construire le schéma-blocs de simulation de la commande vectorielle à flux orienté de la machine asynchrone.

Ainsi, le travail commencera dans un premier temps, par la conception des différents correcteurs et après, de la simulation du démarrage direct suivi de la simulation de la commande vectorielle indirecte à flux rotorique orienté avec régulations de courant et de vitesse.

Caracteristiques de la machine etudiee

- Puissance nominale: 3kW ; - Résistance stator : R_s = 2,5 7 Ù

- Vitesse nominale: 2800tr/min ; - Inductance cyclique stator : L_s = 0,53 H

- Courant nominal : 10A/6A - Constante de temps rotorique: ô r = 0,4 s

- Tension statorique: 230V/400V - Moment d'inertie du rotor : J = 0, 0162 kg.m²

- Couple nominal : 10,3 N.m

- Coefficient de dispersion de Blondel : ó = 0,03 9



- Coefficient des frottements visqueux : f = 0,001N.m. ^s rad

I- Conception des differents blocs dans Simulink

I.1- Blocs de transformation

Comme indiqué dans le chapitre précédent, nous utiliserons la transformation permettant de passer directement du système abc au système dq de Park ; et ceci à travers la matrice P(è) . Le schéma-blocs Simulink est donc le suivant :



Figure 2-1 : Schéma-blocs de la transformation abc » dq

De la même manière, on construit le schéma-blocs de la transformée inverse (dq à abc).

Apres encapsulation des deux, on obtient les quatre blocs de transformation (tensions et courants) nécessaires ci-dessous :



Figure 2-2 : Blocs de transformation directe et inverse nécessaires

I.2- Bloc Machine Asynchrone

Le système d'équation d'état (1.15) tel qu'écrit, permet facilement la simulation de la machine en régime transitoire à partir d'un programme écrit sous Matlab.

Mais pour la simulation avec Simulink, nous avons choisi de l'écrire plus simplement (simple
transformation) en posant ø rd = MImd et ø rq = MImq , sous la forme ci-dessous indépendante

de la mutuelle et facilitant la mise en schéma-blocs.

Equations électriques :

V R L p I

= +

( ó ) - ù ó - ( ) ( )

1 - + -

1 ó

sd s s sd s s sq

L I ù ó L I L

s s mqs

VR L p I

= +

( ó ) + ù ó + ( ) ( )

1 - + -

1 ó

sq s s sq s s sd

L I ù ó L I L

s s md s

( )

1 + ô ù ô

r p I I

= +

md sd r r

~ ( 1+ ô rp)I mq = I sq - ùrôr

Equations mécaniques :

( Jp + f)Ù= 1)( 1 - ó) L ,1I mdI sq-ImqI sd] - C _r= C _em -Cr

ù_r = ù_s- iÙ

~~

~

I_mq

I md

dImd

dt

dImq

dt

(2.1)

Ce modèle présente une particularité fondamentale dans la mesure où elle ne tient pas compte des paramètres du rotor (résistance et inductance) qui ne sont ni accessibles ni mesurables pour un rotor à cage.

Donc, indépendamment de la construction de son rotor, la machine asynchrone triphasée peut être caractérisée par les six paramètres mesurables ci-dessous :

· électriques : R_s , L_s , ô_r et ó .

· Mécaniques : J et f .

Pour ce projet, les valeurs de ces paramètres données ci-dessus correspondent aux résultats de l'indentification de la machine que nous avons effectuée en Laboratoire en vue de la simulation et dont les détails de manipulation seront donnés dans le prochain chapitre. L'ensemble de ces six équations permettent donc de construire le schéma blocs (Simulink) cidessous qui représente le moteur asynchrone dans le repère (d , q ) de Park choisi.



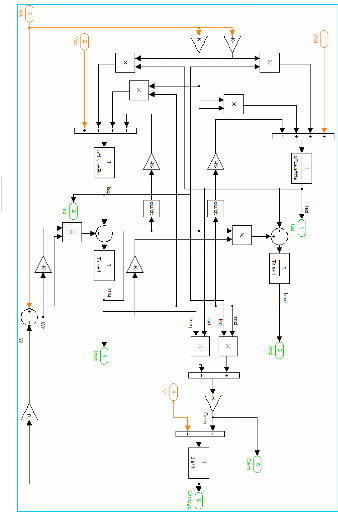
Figure 2-3 : Schema-blocs de la MAS dans le repere (d,q) de Park

L'association des blocs de transformation et du modèle de la machine ci dessous, permet d'avoir le schéma-blocs global de la machine asynchrone en abc ci-dessous :



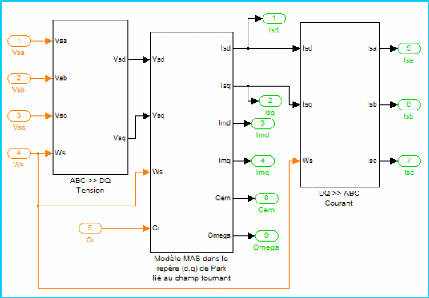
Figure 2-A : Schema-blocs de la MAS dans le repere de Park

Ce qui encapsulé, nous donne le bloc Machine Asynchrone en abc ci-dessous, utilisé pour la simulation.



Figure 2-5 : Bloc MAS reelle

1.3- Bloc On duleur



Figure 2-6 : Bloc On duleur



Figure 2-7 : Bloc Orientation

du flux rotorique



Figure 2-8 : Bloc Autopilotage

Il s'agit simplement d'un bloc contenant le premier ordre pour chacune des phases. Les entrées étant les tensions de référence fixées par les courants de référence et les sorties les tensions d'alimentation de la machine.

1.4- Bloc Orientation du flux rotorique

L'équation (1.19) de la loi d'orientation du flux rotorique permet de construire le bloc ci-contre :

1.5- Bloc Autopilotage

L'équation (1.21) de la loi d'autopilotage permet de construire le bloc ci-contre :

1.6- Bloc Régulateur



Les correcteurs étant tous de type PI, on peut les encapsuler chacun et obtenir le bloc ci contre, avec la référence en entrée et la sortie corrigée.

Figure 2-9 : Bloc Régulateur

1.7- Bloc Découplage (par compensation) Il s'agit simplement du bloc correspondant à au découplage par compensation des commandes des deux axes d et q , illustré à la figure 1.7.

Figure 2-10 : Bloc Compensation

II- Simulation du démarrage direct de la machine asynchrone reliée au réseau

En alimentant directement (réseau EDF) la machine (modèle de la figure 2-7) par une source triphasée de tensions équilibrée de fréquence 50Hz, on obtient les résultats ci-dessous :



e- Courant Statorique Isa

c- Vitesse angulaire

a- Courant Is

- Couple électromagnétique

b- Courant Isq

Figure 2-11 : Résultats de la simulation du démarrage direct de la MAS

111- Synthese des regulateurs ( de type P1)

Pour la simulation, les correcteurs seront simplement synthétisés en continu (forme symbolique de Laplace) contrairement à l'expérimentation où les correcteurs devront tous être discrets (utilisation du DSP).

Les régulateurs sont de type PI car comportent une action proportionnelle qui sert à régler la rapidité de la régulation et une action intégrale qui sert principalement à annuler l'erreur statique en régime permanent.

111.1- Modelisation de l'onduleur a ML1

Le convertisseur statique qui est un onduleur de tension contrôlé en courant, introduit un
retard statistique pur (temps mort, protections, commande des interrupteurs statiques, temps

T

.

de conversions, etc...) représenté par : e

- p 2

T

.

-p

La fonction de transfert de l'ensemble (onduleur-commande rapprochée) est G0 e2 G₀ étant le gain statique de l'ensemble.

Mais pour simplifier le calcul des différents correcteurs, nous ne considérons que le retard de
l'onduleur et la fonction de transfert de l'ensemble (onduleur-commande rapprochée) sera

assimilé au premier ordre	1	. Donc G 0 = 1 .
	1+ pT



L'identification à un système du second degré :

, donne :

1

2m 1

p + p

_ù2

0

1+

2

ù₀

111.2- Correcteurs de courant

Le schéma bloc pour l'axe d devient donc :



Figure 2-12 : Boucle de regulation des courants

1

1 + T p 1 R

La fonction de transfert en boucle ouverte (FTBO) est : ( ) ( p)

i s

H K

= . . .

0 ^p T p 1 + Tp 1 + óô

i s

Le critère de compensation du pole le plus lent nous permet d'écrire : T_i = óô s

.

K 1

et donc : H₀ = p .

R_s óô _sp( 1+ Tp)

La fonction de transfert en boucle fermée (FTBF) est : K_p

H

1

= =

T_p 2

^f K R p R Tp

+ + R R _s óô

p s óô óô

s s s s óô s s

1 +

K p

K p

p +

1 Pour un coefficient d'amortissement 0,7 m = 2

(dans le cas habituel), les abaques des

ù0 =

K p

et

m

=

1

Rsóôs

R s óôsT

2

K pT

.

dépassements et des temps de réponse (annexe...) donnent : ù₀ t_r 3, et D (%) 5 .

A une fréquence de fonctionnement de l'onduleur de 20kHz (protection de l'oreille humaine)
correspond une période T_MLI = 5 0ìs . En prenant un retard de régulation du courant

T rég _ I 200 ì s [9], on obtient la constante de temps de l'onduleur : 250ìsis

R óô

Ce qui permet d'avoir : s ó et T_i = óô _s .

L

s s

K p 2

= =

T 2

0,03 9 0,5 3 × AN : 4 1,3 4 Kp = 6 = 2 250 . 1 0 - ×

0,03 9 0,5 3 = × et 0,00 8 Ti = 02,575

La fonction de transfert du correcteur est : C_I C( p) p= 4 1,3 4 . 1+10,00 808

0, 0 08 p

Aprèseréglagege deparamètreses du correcteur pour arriveà a annulel'erreurur statique touen en gardant un bon temps dréponse,e, on retient

1 0,00 8 p ( ) 3 6,65 . +

1 0,00 8 p

Axe d : C_Id p

( ) 3 6,65 . +

= et axe q : C_Iq p =

0,00 8 p p 0,0 08p

111.3- Correcteur de vitesse

Dans unrégulationon en cascade, la boucle interne est toujours beaucoup plus rapide que la boucle externe. Ainsi, enégligeantanl'influencece de la boucle de courant sula la dynamique de vitesse, lschémama simplifié drégulationon ed'asservissementnt de la vitessest st le suivant :



Figure 2-13 : Boucle d régulationon de la vitessK pv p + K iv , On a : ( )[ C _em C _r ]

Ù = 1

Jp f - . Avec le régulateur PI classique

+ p P

f) f)Kpv p+Kivp ^von obtient : : ( Jp + p( Jp+pf) fCrCT

K p K

+ p

pv iv *

Soit : ( )

Ù = Ù ?

2 2 ( ) r

C

Jp K f p K

+ + + Jp K f p K

+ + +

pv iv pv iv

2m Kpv +

=

ù₀ K_iv

L'identification à un système du second degré donne :

J

1 =

et

ù ²

0

K_iv

f

.

Pour un amortissement m = 1 , on a ù₀ t_r 4,75 , on obtient les paramètres du correcteur :

2

~ 4,75 ~ 9,5 -

K J

= ~ ~ et f

K J

pv =

iv ~ t r ~ t r

On désire obtenir un temps de réponse en vitesse t_r = 500 ms = 0,5 s .

0,5

AN :

	Kiv = 0, 0162	~ × ~ ~	4,75	2 ~ 0,1 ~ 1,46 K	62 ×	9,5 0,00 1 =	0, 3078
				= et v = ~	0,5

Après réglage et ajustement de ces paramètres pour avoir le moins de dépassement possible

K

(influence du zéro présent dans la FTBF), on obtient : K iv = K v = 0,5 et = = 4

v

K . Le

^pv T

v

C_v ( p) = 0,5 . 1 + 0,1 25

0,1 25 p

p

correcteur de vitesse retenu est donc :

IV- Simulation de la comman de vectorielle in directe a flux rotorique orienté

Nous allons maintenant procéder à la simulation de la commande vectorielle qui est l'objet principal de ce chapitre et de ce projet. La simulation concernera dans un premier temps la commande en mode non découplée (avec les deux axes couplés comme naturellement) et enfin la commande en mode découplé (avec les deux axes découplés).

IV.1- Calcul des valeurs nominales des références

IV.1.1- Valeur nominale Isdn du courant d'axe d

D'après la relation (1.27), la valeur nominale _Isdn du courant d'axe d est, en régime permanent, celle du courant magnétisant I_mrn absorbé à vide (couple nul). Ce qui en réalité, est vrai lorsqu'on néglige la chute de tension dans la résistance statorique. On a ainsi :

V 230

sn

V 0 = V = X I = L ù I ? I = = = 1,3 8 A



s sn m mdn s sn mdn mdn L 0,53 100

× ð

s sn

ù

-



D'après la relation : I s = I _sd + jI sq

I mrn = I sdn = 3 I _mdn [10].

tirée de la transformation de Park, on obtient :



AN : I_sdn = 3 × 1,3 8 = 2,3 9 A . Donc I_sdn 2,5 A .

IV.1.2- Valeur nominale Isqn du courant d'axe q

Connaissant le couple nominal du moteur, l'expression (1.23) permet de déduire la valeur nominale du courant I_sq , lorsque le courant magnétisant est lui-même à sa valeur

nominale.

On a : / = = 1 0,3 = 8,46 A . Donc I_sqn = 8,46 A

sqn C _un

(1-- ó) LsI sdn ( 1- 0,03 9 )× 0,5 3 × 2,3 9

IV.1.3- Valeur nominale Ù n de la vitesse

La machine étudiée étant unipolaire et alimentée à la fréquence de 50Hz, a une vitesse de synchronisme de 3000tr/min. Ce qui correspond à une vitesse angulaire d'environ 314rad/s. Donc Ù_n =100ð rad / s .

Les valeurs nominales obtenues et retenues pour les différentes consignes de commande, sont les suivantes :

Isdn 2,5 A ; Isqn = 8,5 A et Ù_n 3 1 4,3 rad / s

IV.2-Illustration du decouplage de la comman de des axes d et q

- Pour 0 < t = 0,5 s, les consignes I _IsdREF et _IIsqREF sont respectivement fixées à 2,5A et 0. - Pour 0,5 < t = 1s , on procède à un échelon de IIsqREF = 8 A , sans modifier I _IsdREF .

- Pour t > 1 s , on ramène la consigne _IIsqREF à 4A.



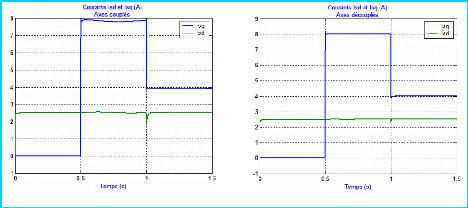
a- Axes d et q co uples b- Axes d et q d:couples

Figure 2-14 : Boucle de regulation de la vitesse

IV.3.Comman de vectorielle en mode non decouplee (sans compensation)

En associant tous les blocs nécessaires construits précédemment, nous sommes parvenus à réaliser le schéma de la simulation ci-dessous qui correspond à celui de la figure 1.10 du chapitre précédent sur lequel, a été rajoutée la boucle de régulation de la vitesse.

Chapitre 2. Simulation de la commande vectorielle a flux rotorique °dente avec Matlab/Simulink.		27 Rapport de projet realise, redige et presente par Danic TOFFESSI YAPTA Master 2 SEE-Energie Electrique, UHP - Nancy 1, 2009/2010
	Figure 2-15 : Schema de la simulation de la comman de vectorielle in directe a flux oriente avec couplage des deux axes d et q de la machine asynchrone (MAS naturelle) avec Simulink

R ésultats de la simulation :



e- Courant statorique Isa

c- Vitesse angulaire

a- Courant Is

- Couple électromagnétique

f- Tension statorique Vsa

b- Courant Isq

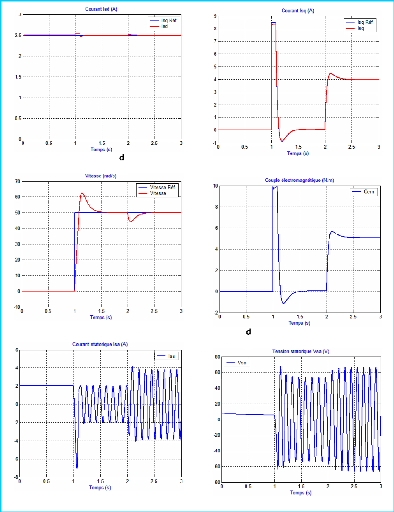
Figure 2-16 : Résultats de la simulation de la comman de vectorielle a flux rotorique orienté de la MAS

(Sans compensation)

La simulation a été effectuée sur une durée de 3 secondes de la manière suivante : - La consigne I _IsdREF est maintenue constante à sa valeur nominale 2,5A.

- Pour 0 < t = 1s , la consigne de vitesse Ù _REF est nulle.

- Pour 1 s < t = 2s , on procède à un échelon de Ù _REF = 50 rad / s , le couple de charge restant

nul (fonctionnement à vide).

- Pour t > 2 s , Ù _REF reste fixée à 50 rad/s et on injecte brusquement une charge imposant à la

machine un couple résistant de 5 N.m, correspondant à peu près la valeur 4A du courant _IIsq .

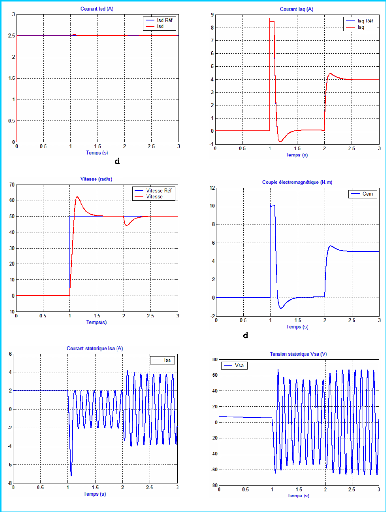
IV.4- Comman de vectorielle en mode découplée (avec compensation)

Le schéma en mode découplé est exactement le même qu'en mode couplé, en plus du bloc de compensation (découplage).

La simulation a été effectuée de la même manière et dans les mêmes conditions que précédemment.



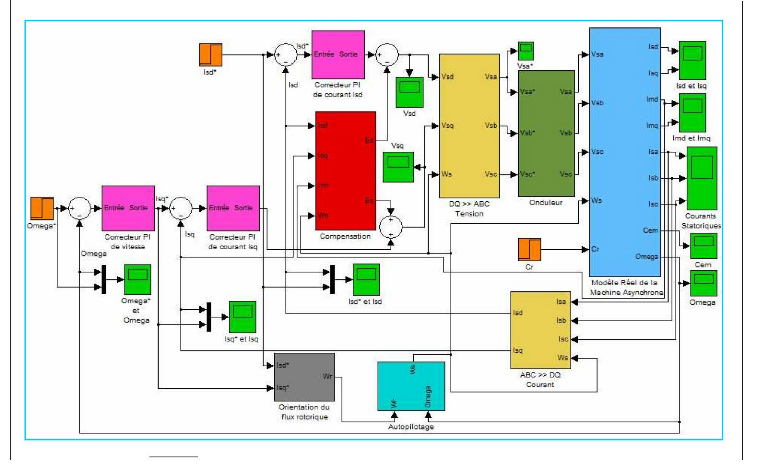
Figure 2 -17 : Schema de la simulation de la comman de vectorielle in directe a flux oriente avec decouplage
des deux axes d et q, de la machine asynchrone (MAS decouplee) avec Simulink

Chapitre 2. Simulation de la commande vectorielle a flux rotorique °dente avec Matlab/Simulink.

30

Rapport de projet realise, redige et presente par Danic TOFFESSI YAPTA Master 2 SEE-Energie Electrique, UHP - Nancy 1, 2009/2010

Résultats de la simulation :



e- Courant statorique Isa

c- Vitesse angulaire

a- Courant Is

- Couple électromagnétique

f- Tension statorique Vsa

b- Courant Isq

Figure 2-18 : Résultats de la simulation de la comman de vectorielle a flux rotorique orienté de la MAS

(Avec compensation)

Inversion de vitesse de 100 ra d/s a - 100 rad/s



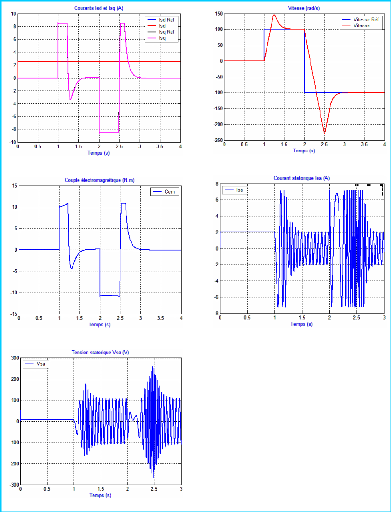
c- Couple électromagnétique

f- Tension statorique Vsa

a- Courants Isd et Isq

e- Courant statorique Isa

b- Vitesse

Figure 2-19 : Résultats de la simulation d'une inversion de vitesse de 100 ra d/s a - 100 rad/s, en comman de vectorielle in directe (Avec compensation)

Conclusion

A partir de ces résultats de simulation, on peut effectivement prévoir le comportement de la machine en régime dynamique. Cette simulation a permis par exemple de voir l'influence du découplage des commandes des deux axes ; découplage qui n'est pas parfait mais qui réduit considérablement leur dépendance, l'une de l'autre.

Le dépassement de la vitesse augmente avec l'amplitude de la consigne. Ce qui peut être acceptable en simulation et non dans la réalité où des régulateurs IP Anti Wind-up sont utilisés pour réduire au maximum (à défaut d'éliminer) les dépassements de vitesse ; ce qui se verra en expérimentation, par rapport à la simulation.

Chapitre 3 : EXPERIMENTATION DE LA COMMANDE VECTORIELLE A FLUX ROTORIQUE ORIENTE DE LA MACHINE ASYNCHRONE

Introduction

Après la phase de simulation qui a permis de prévoir le comportement et le fonctionnement de la machine asynchrone en régime dynamique, il vient la mise en oeuvre pratique et l'expérimentation de la commande envisagée. Cette phase d'expérimentation permettra essentiellement de valider le model, jusqu'ici étudié et simulé.

Dans ce chapitre, il s'agira tout d'abord de l'expérimentation du démarrage direct de la machine asynchrone. Ensuite d'expliquer brièvement le principe et la procédure de mise en oeuvre à travers les différents composants nécessaires ; sachant que l'ensemble du système est piloté par un DSP (Digital Signal Processor). Enfin, on passera à l'expérimentation proprement dite de la commande vectorielle à flux rotorique orienté.

I- Principe de la mise en oeuvre

I.1- Schema de principe

Le schéma de principe utilisé pour cette expérimentation en laboratoire est le suivant :



DSP

Coeur du système

Bloc Convertisseur Statique

Banc machine

Figure 3-1 : Schema de principe d'expérimentation de la comman de vectorielle

I.2- Description des différents blocs

- Bloc Convertisseur statique : Monté au secondaire d'un autotransformateur et constitué d'un pont redresseur triphasé PD3, suivi d'un onduleur triphasé alimenté avec une tension continue de 500V et fournissant les tensions d'alimentation de la machine (230V/400V).

Ce bloc contient aussi d'une part trois capteurs de courants (dont les sorties sont accessibles) montés sur les trois phases alimentant la machine. Il est d'autre part muni d'un connecteur BNC pour les échanges de données avec le DSP, sans oublier toute la sécurité des interrupteurs de puissance.

- Bloc Machine : Constitué de deux machines asynchrones identiques (l'une entraînant l'autre), suivi d'un codeur incrémental comme capteur de vitesse. La première machine asynchrone (celle étudiée) fonctionnant en moteur et alimentée par l'onduleur triphasé.

- Bloc Filtrage : Il s'agit simplement d'un boîtier comportant des filtres permettant d'éliminer les bruits dans les mesures de courants, de vitesse ou de position avant leur arrivée dans le DSP pour traitement. Pour des raisons de temps et de simplification, nous n'avons pas tenu compte de ces filtres (modélisés par un premier ordre) dans le calcul des différents correcteurs.

- Bloc Pilotage (DSP) : Il s'agit essentiellement du microcontrôleur (de type ds1104 du fabricant dsPACE) et de tout son environnement, permettant de piloter tout le système et de réaliser la commande vectorielle ; puisqu'il contient tous les programmes et algorithmes de commande. Cette partie sera mieux détaillée dans le paragraphe suivant.

- Ordinateur de contrôle : Il s'agit simplement de l'interface (dsPACE Control Desk) de communication entre l'homme et la machine à travers le DSP et tous les éléments en aval. De cette interface, on donne toutes les consignes (courant, vitesse,...) au DSP qui les applique à travers les programmes et renvoie les résultats qui peuvent être visualisés dans l'interface.

II- Pilotage de l'ensemble du systeme

C'est sans doute la partie la plus importante pour la réalisation d'une commande vectorielle et même de toute commande numérique. Ce rôle est donc ici, rempli par le DSP ds1104 (coeur du système).

II.1- Programmation du DSP

Le DSP contient donc tous les programmes et sous-programmes (fonctions) relatifs aux différents algorithmes de commande et écrits en langage C++.

Description des diffé rents programmes

Comme dit précédemment, le DSP contient le programme principal (fonction main) qui fait appel aux fonctions relatives aux algorithmes d'acquisition, de transformation de Park, de contrôle vectoriel, d'autopilotage, de régulation, de PWM, ...

Des extraits de ces fonctions sont donnés en annexe 2.

- Programme principal (fonction main) : indc.c

Cette fonction principale nommée indc.c est celle qui gère la MLI, appelle les fonctions (sous-programmes), initialise les variables et gère la sécurité des interrupteurs de puissances et de tout le système.

- Fonction Acquisition : ACQUI.C

Cette fonction gère l'acquisition des courants et de la vitesse mesurés respectivement à l'entrée et à la sortie (codeur) de la machine et calcule par ailleurs la pulsation mécanique. Sachant que pour cette commande, il n y a besoin que de deux courants de deux phases ; le troisième étant fabriqué à partir de ceux-ci qui arrivent au niveau du DSP par les pins 2 et 3 configurées en entrées analogiques et la vitesse par la pin 4 configurée en entrée logique (numérique).

- Fonction Transformation : TRANS.C

Elle contient les algorithmes des transformations de Clarke (passage système triphasé abc au système diphasé áâ ) et de Park (passage du repère fixe (á ,â ) à un repère tournant

(d ,q ) dit de Park).

- Fonction Régulation : REGUL.C

Elle contient les algorithmes de calcul de l'angle des transformations, des régulations de courant et de vitesse. Elle intègre aussi une boucle de régulation de vitesse IP (Intégral et Proportionnel) Anti Wind-up qui permet de réduire à défaut d'annuler les dépassements de vitesse.

- Bibliothèque : VAR.H

Simplement, elle contient les déclarations et définitions de toutes les constantes et variables nécessaires et utilisées dans les fonctions.

11.2- Discretisation des correcteurs

Le DSP travaillant en (discret) numérique, il s'agit ici de calculer l'équivalent discret des correcteurs PI continus (utilisés pour la simulation) en vue de l'expérimentation

Pour un système continu, on a :



C( p ) = K_pc . T_c p = K + ^pc

et y ( p ) = R(p ) . e ( p )

p

T p pc

1+ Tc c

Pour un système discret, on a :

k

y k K _pd e k K id e i

( ) = ( ) . ( )

+ ~ ? ( ) ( 1) ( ( ) ( 1) ) ( )

y k y k

- - = pd

K e k e k

- - + id

K e z

i=0

Une transformation en z donne :

y z z y z K ( ) - - 1 ( ) = pd	( e(z ) - z^-1 e (z ) ) + K e (z) id	~ K ~ id ? y z K ( ) = ~ + 1 e z ~ ( ) (3.1) pd - ~ 1 - z ~
~ En posant pTe id z = e , on a : e 1 - z = 1 - e pTe pT . Donc ( ) = ~ + K y p K ~ ~ e ( p ) pd ~ pTe ~			(3.2)

L'identification de (3.1) et (3.2) permet d'avoir :

K pc

K pd = K _pc et e

K = T

^id T

ic

- En courant : Le retard de régulation de courant est Trég _I = T_eI 200ìs .
AN : K pd = K pc = 3 6,65 et K K pc T = 3 6,6 5 × 200. 1 0 -6 = 0,92

^id T _ic^e0,008

- En vitesse : Le retard de régulation de la vitesse est Trég _ Ù= TeV 1 ms .

K 0,5

pc

AN : K pd = K pc = 0,5 et K = T = × - 3 =

10 0,004

id e

T 0,1 25

iv

On a ainsi retenu :

C ( p) = 3 6,65 + 0,92 et Vitesse :

^id TeI

Axes d et q :

p

C _vd

0,005

T eVp

( p) = 0,5 +

III- Resultats experimentaux

L'interface utilisée ici pour cette commande est l'environnement dsPACE du logiciel dsPACE Control Desk du fabriquant dsPACE. Ce qui a permis de visualiser les courbes et de récupérer des tableaux de données conduisant aux courbes expérimentales ci-dessous. Des images d'illustration (de cette interface) sont données en Annexe 3.

L'expérimentation est effectuée pour une commande en mode découplée ; puisque les commandes des axes d et q de la machine sont naturellement couplées.

III.1- Echelon de courant Is

En procédant à un échelon du courant Isd de 1A à 2,5A, On a relevé les réponses ci-dessous :



e- Courant statorique Isa

a- Courant Is

c- Vitesse

- Couple électromagnétique

f- Tension statorique Vsa

b- Courant Isq

Figure 3-2 : Réponses a un échelon de courant Is d de 1A a 2,5A

III.2- Echelon de vitesse de 50 ra d/s

Le courant Isd étant maintenu à 2,5A, en procédant à un échelon de vitesse de 50 rad/s, On a relevé les réponses ci-dessous :



c- Couple électromagnétique

e- Tension statorique Vsa

a- Courants Isd et Isq

- Courant statorique Isa

b- Vitesse

Figure 3-3 : Réponses a un échelon de vitesse de 50 ra d/s

III.3- Echelon de vitesse de 200 ra d/s

Dans les mêmes conditions initiales (courant Isd maintenu à 2,5A et vitesse nulle), en procédant à un échelon de vitesse de 200 rad/s, On a relevé les réponses ci-dessous :



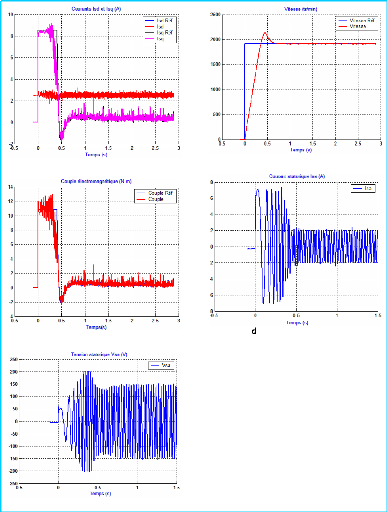
c- Couple électromagnétique

e- Tension statorique Vsa

a- Courants Is d et Isq

- Courant statorique Isa

b- Vitesse

Figure 3-4 : Réponses a un échelon de vitesse de 200 ra d/s

III.A- Inversion de vitesse de 100 ra d/s a - 100 rad/s

Le courant Isd étant maintenu à 2,5A et la vitesse à 100 rad/s, on a procédé à une inversion de vitesse (de 100 rad/s à -100 rad/s) et on a obtenu les réponses ci-dessous :



c- Couple électromagnétique

e- Tension statorique Vsa

a- Courants Isd et Isq

- Courant statorique Isa

b- Vitesse

Figure 3-5 : Réponses a une consigne d'inversion de vitesse de 100 ra d/s a - 100 rad/s

III.5- Echelon de couple résistant

Le courant Isd étant maintenu à 2,5A et la vitesse à 100 rad/s, on a procédé à un échelon de couple résistant (par un freinage par injection de courant continu) et on les réponses sont :



c- Couple électromagnétique

e- Tension statorique Vsa

a- Courants Isd et Isq

- Courant statorique Isa

b- Vitesse

Figure 3-6 : Réponses a un échelon couple résistant

En effet, cet échelon de charge a été donné à la machine étudiée à travers un freinage par injection de courant continu sur la deuxième machine asynchrone du banc d'essai.

Conclusion

De ces résultats expérimentaux, on voit que pour un échelon, le courant Isd monte et s'établit en 10ms alors que le flux dans la machine prend un retard de l'ordre de la constante de temps rotorique.

On voit aussi les effets positifs non seulement du découplage sur les commandes des deux axes lors d'un échelon de vitesse, mais aussi et surtout des régulateurs IP Anti Wind-up à travers le dépassement de la vitesse qui est nulle pour un échelon de 50 rad/s et qui est de l'ordre de 10% pour un échelon de 200 rad/s. Ce qui confirme ce que le dépassement pour le correcteur de vitesse calculée, augmente avec l'amplitude de la référence.

On peut aussi voir les effets de la limitation (saturation) du courant Isq à sa valeur maximale (8,5A/-8,5A) sur le couple électromagnétique lors d'échelons de vitesses importantes (démarrage, inversion de vitesse,...).

Lors d'un échelon de charge (perturbation de la vitesse), la régulation de vitesse est très effective et se fait en moins d'une demi seconde.

Malgré le filtrage, les courants Isd et Isq sont bruités ; ce qui se répercute sur le couple électromagnétique.

Conclusion générale.

CONCLUSION GENERALE

Au terme de ce rapport de projet basé sur la commande vectorielle à flux rotorique orienté d'une machine asynchrone triphasé, force est de dire que ce travail nous a permis de découvrir un nombre important d'aspects de la recherche scientifique ainsi que de la mise en oeuvre et réalisation pratique d'un système de commande de machine électrique.

D'une part, La modélisation de la machine asynchrone à partir de ses équations de fonctionnement, le choix et l'élaboration d'une stratégie de commande, l'identification des paramètres, le calcul des différents régulateurs, la simulation du démarrage direct et de la commande vectorielle envisagée et d'autre part, l'expérimentation du démarrage direct et de la commande vectorielle sommairement les points sur lesquels nous nous sommes attardé pour mener à bien ce projet.

Malgré les difficultés (faute de temps) de montage d'un banc d'essai bien adapté (MAS+MCC+Codeur) qui nous a conduit à utiliser un autre banc d'essai (MAS+MAS+Codeur), d'utilisation de méthodes d'identification assez fiables et aussi de programmation du DSP, nous avons pu atteindre les objectifs non seulement techniques mais aussi et surtout pédagogiques portés par un tel projet. Et ce, à travers les résultats obtenus en simulation et en expérimentation.

Les résultats de la simulation et de l'expérimentation diffèrent sensiblement au niveau des temps de réponses et amplitudes des signaux, puis au niveau des bruits contenus dans les mesures expérimentales. Ce qui peut s'expliquer par la géométrie des enroulements, le manque de précision dans l'identification des paramètres de la machine (incohérences des paramètres) ainsi que la sensibilité paramétrique (réelle) qui n'a pas été pris en compte dans la simulation (par exemple la constante de temps rotorique qui varie avec la température). L'onduleur à MLI de son coté produisant une forte ondulation de la tension qui se répercute sur les courants qui sont bruités.

REFERENCES BIBLIOGRAPHIQUES

[1]- Comman de vectorielle sans capteur des machines asynchrones Claude Chaigne ; Erik Etien ; Sébastien Cauet ; Laurent Rambault Editions Lavoisier 2005

[2]- Comman de vectorielle de la machine asynchrone

Benoit Robyns ; Bruno Francois ; Philippe Degobert ; Jean-paul Hautier Editions TECHNIP 2007

[3]- Comman de électronique des moteurs électriques Michel Pinard - Série EEA

DUNOD

[4]- Actionneurs électriques (Principes et modales) Guy Grellet ; Guy Clerc

Eyrolles

[5]- Mo délisation, contrôle vectoriel et DTC (commande des moteurs asynchrones ¹) Carlos Canudas de Wit

Germes Sciences

[6]- Mo délisation et comman de des moteurs triphasés Guy Sturtzer ; Eddie Smigiel

Ellipses

[7]- Principes d'électrotechnique

Max Marty ; Daniel Dixneuf ; Delphine Garcia Gilabert Dunod

[8]- Contribution a la comman de des machines asynchrones (Rapport de stage D.E.A) Aissa Dalila

ENSEM, Septembre 1994

[9]- Comman de vectorielle d'une machine asynchrone a enroulements de mesure de F.E.M (Rapport de stage D.E.A)

L. BAGHLI ; Green-UHP, Juillet 1995

[10]- Mo délisation et comman de de la machine asynchrone Jean -Pierre Caron ; Jean-Paul Hautier

Editions TECHNIP

[11]- Comman de vectorielle des machines asynchrones et synchrones JM RETIF

Cours INSA Lyon, 2008

[12]- Comman de vectorielle de machine asynchrone en environnement temps réel Matlab-Simulink (Mémoire du diplôme d'ingénieur)

Gabriel Buche

C.N.A.M Grenoble, Mars 2001

[13]- Mo délisation et Comman de de la machine asynchrone J.P. CARON ; J.P. HAUTIER

Editions Technip 1995

[14]- Mo délisation et Comman de de la machine asynchrone L. BAGHLI

Notes de cours, 2005

[15]- Régime dynamique des ensembles convertisseurs- machines A. Rezzoug

Notes de cours, Master 2 SEE-UHP, 2009/2010

[¹5]^- Comman de des machines électriques A. Rezzoug

Notes de cours, Master 2 SEE-UHP, 2009/2010

ANNEXES

Annexes.

ANNEXE 1 : IENTIFICATION DES PARAMETRES DE LA MAS

Plaque signaletique :

- Puissance : 3kW

- Vitesse : 2800 tr/min

- Tension : 230V/400V

- Courant : 10A/6A

- Facteur de puissance : 0,94

Le banc d'essai est constitué de deux MAS identiques, l'une entrainant l'autre à vide.

I- Mesure de la resistance statorique Rs Matériels utilisés :

- 01 source de tension continue (0-240V) ; - 01 voltmètre

- 01 ampèremètre

1- Mesure a l'ohmmetre Une simple mesure à l'ohmmètre effectuée à chaud nous a donné : R_s 3,5Ù

2- Methode voltamperemetrique Les relevés effectués sont récapitulés dans le tableau ci-dessous :

E(V)	2	4	5		6		10	15	17
I(A)	1	1,7	2		2,3		3,6	5,2	5,9
Rs()	2	2,35	2,5		2,6		2,77	2,88	2,88
Le calcul de la valeur moyenne donne :				Rs 2,5 7 Ù

II- Essai a vide

1- Mesure de l'inductance cyclique statorique Is Matériels utilisés :

- 01 autotransformateur (alternostat) ;

- 01 voltmètre

- 01 ampèremètre

- 01 pince Fluke

Le montage réalisé est le suivant :

Les relevés effectués sont récapitulés dans le tableau ci-dessous :

P(W)	Q(Var)	S(VA)	I(A)	U(V)	Cos?
340	950	1020	1,45	400	0,34

Le bilan de puissance réactive donne :

V

(400)

Q₀ = V 3 ? L s = 3 = = 0,53

Q ₀ù_s 950× 100ð

L_s 0,53 H

2

2

2

X_s

2- Mesure de la constante de temps rotorique ôr

Matériels utilisés :

- 01 autotransformateur (alternostat), avec contacteur d'arrêt et de mise en marche ; - 01 voltmètre

- 01 ampèremètre

- 01 sonde différentielle de tension

- 01 Ordinateur + Outil dSpace pour acquisition

Le schéma de montage est en dehors du dispositif d'acquisition, identique au précédent. La machine étant en régime nominal, la coupure brutale et simultanée des trois phases d'alimentation a donné la courbe de décroissance de la tension ci-dessous :



Figure 1 : Décroissance de la tension statorique apres coupure brutale des trois phases d'alimentation

Cette tension a la forme d'une sinusoïde amortie à la constante de temps rotorique ô_r . Les

t

-

deux grandeurs étant liées par une relation de la forme : ( ) = cos( - ) .

r

V _as t A ù î

s t e ^ô

La constante de temps rotorique sera donc déterminée ou simplement lue dans l'une des deux enveloppes exponentielles (inférieure ou supérieure).

Méthode 1 : Lecture de la constante de temps

Dans l'enveloppe supérieure, la tension statorique va de sa valeur maximale 311V à 0. Donc l'instant où elle vaut 63% de sa valeur finale (0V dans ce cas) correspond à 27% de 311V, soit 83,87V.

A t1=0,834s, Vas=311V

A t2=1,43s, Vas=83,87V

D'où la constante de temps rotorique : ô r 0,5 96 s

Méthode 2 : Calcul de la constante de temps

On démontre que pour deux instants t1 et t₂ ( t₂ > t1 ) correspondant a des passages par des points respectifs V_{as 1} et V_{as 2} , communs à l'enveloppe choisie, la constante de temps se

calcule par la formule :

ô = - ( t₁ -t₂)

.

₂1)

r

Vas

lnVas





-

0,5 96 =

.

Pour les deux points ci-dessus, on a : r

ô = 0,454 s

ln

(³3¹,8 83,87 j

Une troisième méthode sera appliquée avec l'essai à rotor calé, dans la suite.

3- Mesure du moment d'inertie J

3.1- Pertes mécaniques pm : Coefficient des frottements visqueux f La puissance active absorbée a vide est composée de :

- Pertes joules statoriques : 3RsIo²

- Pertes fer : Pf=3V²/Rf

2

2

- Pertes mécaniques : pm

V V

2

P = R I +

0 3 0 3

² + 0 3 0 3

p +

s m ? p aV b

2

P R I

- s = + =

m

R R

2

f f

Ce qui est l'équation d'une droite ; avec a = 3 ^V et b = p_m . Il suffit donc de tracer cette

R_f

caractéristique pour déterminer a et b .

Les relevés des différentes grandeurs ont permis de tracer la courbe ci-dessous :

					Figure 2 : Caractéristique a vide Po- 3RsIo^2=f(V^2)
D'où : pm 1 00,6 8 W A la vitesse nominale, on : 3.2- Moment d'inertie J	2 pm = f.n0	p -- m	=	1 00,6 8
						f 0,00 1 N.m .s / rad
		0 2 f = Ù		. ,314r (

L'équation mécanique générale de la machine est : T_u - T_r = J ^dÙ .

dt

A vide, la machine ne fournit que le couple des pertes mécaniques. Au voisinage de cette vitesse à vide Ù ₀ (début de la décroissance de la vitesse), on a :

- T _r =-^pm =J

p m

? J = - dÙ ,

dt ( t=0 )

dt (t=0)

dÙ

dt

dÙ

étant le coefficient directeur de la

Ù₀

Ù₀



Figure 3 :

Décroissance linéaire de la vitesse au voisinage de la vitesse a vide

droite de décroissance de vitesse (prise juste au début de la décroissance) au voisinage de la vitesse à vide Ù ₀ . L'allure de cette droite est la suivante :

dt ( t= 0)

2 8,5 3 3

Ce qui permet d'avoir le moment d'inertie : J =- m

dÙ 314× 1 9,48 1

p

Ù₀

= 0, 0046

J = 0, 0046 kg.m²

Le rotor cylindrique de la machine considérée a une masse mesurée d'environ 8kg et un diamètre d'environ mesuré 9cm. Le calcul classique du moment d'inertie nous donne :

1

J 1 = m. r 2 = 8× ( 0,045) ²

2

2 = 0, 0081 kg.m² .

J = 0, 0162 kg.m²

Le banc d'essai étant constitué de deux machines asynchrones identiques, on a le moment d'inertie :

Cette dernière valeur qui résulte d'un calcul très classique, sera retenue puisqu'elle se rapproche le plus de la réalité.

111- Essai a rotor calé

Matériels utilisés

- 01 autotransformateur (alternostat), avec contacteur d'arrêt et de mise en marche ; - 01 voltmètre

- 01 ampèremètre

- 01 pince Fluke

1- Mesure du coefficient de dispersion de Blon del ó

En alimentant le moteur à tension réduite avec son rotor bloqué, on a relevé les données suivantes :

Pcc(W)	Qcc(Var)	Icc(A)	Ucc(V)	Cos?
610	700	5,82	91	0,66

a- Résistance des pertes joule rotoriques

Le courant magnétisent étant ici négligeable devant le courant rotorique ( I₁ I2), on écrit :

' Pc

Pc = 3 ( R ₁ + R;) I ^c2 . Ce qui permet d'avoir : R₂ = ₂ -R₁ = 610 ) 2 - 2,5 7 = 3,43



3 I c3×(5,82

R ; 3,43 Ù

b- Réactance des fuites totalisées L'impédance de l'enroulement vaut :



(52,54 )2

5,82

( 2,57 + 3,43)²

=

X_f

)

2

V_c
I_c

Z = ( R₁ + R ; )² + Xf 2 --V c ?

--

c

- ( R₁ + R; )2

Xf = 6,74 Ù croù :

L f = 0, 0215H

D'après le schéma équivalent de la machine asynchrone ramenée au stator, on a : Méthode 1 :

o^-L_r

, donc ó = Nr

N_r + M

et M = ó Nr

ó

1

~ ~ ~

L _r-M

N L

= ó

r r

L'inductance cyclique des fuites totalisées au stator est :

L f = k² N_r = k² óL avec M

k s

L

= : rapport de transformation inverse.

ó	=	Lf
		L f + Ls

On obtient en remplaçant :

AN : a = 0'0215

5 ₃=0, 0389

0, 0215+0,



. ó 0,03 9

()

Pour g=1, R ;= k²R_r. En développant cette relation avec k² = Ls ² L = , ^s , on aboutit

M L_r(1- ó)

0,5 3

AN : ( ) 0,1 6

ô_r = = ô r 0,1 6 s

1 0,03 9 3,43

- ×

à :	ô r	Ls L s + Lf
		' ( ) ó R ' 1 - R 2 2

Méthode 2 :

L

Connaissant la constante de temps rotorique ô = , on a :

r

r

R_r

ó =X

ô_r

L En formant le rapport '

X f

= , on obtient :

R₂

0, 0215 =

AN : 0,03 9

ó =



3,43 0,1 6

×

Conclusion

Au cours de la manipulation (expérimentation) de a commande vectorielle, on a constaté que la machine avait un problème d'autopilotage (orientation du repère (d , q ) et

calage l'axe d sur le flux) pour la constante de temps rotorique ô r 0,1 6 s. Et ce à travers la dynamique du courant _Isq lors de l'échelon de charge.

Une meilleure dynamique du courant _Isq a ainsi été obtenue pour une constante de

temps ô r 0,4 s

R_s = 2,5 7 Ù ; L_s = 0,5 3 H ; ô r = 0,4 s; ó = 0,03 9

J = 0, 0162 kg.m² ; rad

f = 0,00 1 N . m . s



Les paramètres retenus sont :

ANNEXE 2 : EXTRAITS DE PROGRAMMES ET FONCTIONS

1- Bibliotheque VAR.H : Declaration des constantes et variables

/* Machine (une partie des données) */

//#define Trconst 0.55

#define Trconst 0.4 // Constante de temps rotorique #define P 1

/* constantes */

#define trm2rds 0.10471975511965977461542144610932

#define PI 3.14159265358979323846

#define TWOPI 6.283185307179586

//#define IdsrefBase 0.8 //-- //8.944

#define IdsrefBase 1.0 // Valeur par défaut du courant de la référence Isd*

double IqsrefMax=8.5; // Maximum du courant Isq

// Correcteur de courant volatile double Kpq=36.65; volatile double Kiq=0.92;

// Correcteur de vitesse

volatile double KpW=0.5;

volatile double KiW=0.005;

volatile double KTiW=1.0;

2- Fonction ACQUI.C : Acquisition de courants et vitesse mesurés

#define Aquisition_Courants( i1, i2) \

{ \

i1 = 0.03+20.0*( ds1104_adc_read_conv(2) ); \

i2 = 20.0*( ds1104_adc_read_conv(3) ); \

}

#define inputWm \

{ \

/* read incremental encoder counter */ \

inc_k = ds1104_inc_position_read(1, DS1104_INC_LINE_SUBDIV_4); \

/*inc_k = ds1104_inc_counter_read(1); */\

\

/* calculate mechanical angle rd _ avec inversion _*/ \

mpos=POStoRD*(float)inc_k; \

\

/* calculate mechanical speed rd/s */ \

FIR_Wm[0]=POStoRD_S*(float)( inc_k - inc_kOld ); \

inc_kOld = inc_k; \

3- Fonction TRANS.0 : Transformations de Clarke et de Park

#define C32( Xalpha, Xbeta, Xa, Xb, Xc ) \ { \

Xa=Xalpha; \

Xb=0.8660254038*Xbeta-0.5*Xalpha; \ Xc=-0.5*Xalpha-0.8660254038*Xbeta; \

}

#define 2t( Xa, Xb, Xalpha, Xbeta ) \ { \

Xalpha=Xa; \

Xbeta=0.5773502692*Xa+1.154700538*Xb; \

}

#define Park( Xd, Xq, sin_th, cos_th, Xalpha, Xbeta) \

{ \

Xalpha=Xd*cos_th-Xq*sin_th; \ Xbeta=Xd*sin_th+Xq*cos_th; \

}

4- Fonction REGUL.0 : Regulations de courants et vitesse

/* calcul de thetas, Wsl, Ws et du flux */

#define Calc_thetas \

{ \

Wsl= Iqsref / Tr / Idsref; \

Phidr+=DT*( M*(Ids1+Ids2)-Phidr)/ Tr; \

if (Control_Type==1) Ws=P*Wm+Wsl; \

if (Control_Type!=1) Ws=Wsref; \

th+=DT*Ws; /* 200 us */ \

if ( th > PI) th-=TWOPI; \

if ( th < -PI) th+=TWOPI; \

}

//

void Boucle_PI_Id() {

e=Idsref-Ids;

Vdsref = Kpd*e + xed;

if ( fabs(Vdsref)<=VdsrefMax ) xed += Kid*e;

/* decouplage */

// non valable en MASDE Vdsref-=sigma*Ls*Ws*Iqs;

/* limiteur de tension */

if ( Vdsref>VdsrefMax) Vdsref=VdsrefMax; if ( Vdsref<-VdsrefMax) Vdsref=-VdsrefMax;

}