II.4.1. Présentation de
l'échantillon
L'échantillon est une partie de l'univers, un
sous-ensemble auquel on limitera éventuellement l'observation, soit pour
réduire le coût d'enquête et rendre plus rapide son
exécution et son exploitation, soit parce que la population tout
entière est inaccessible (cas des études de marché et de
certaines enquêtes d'opinion), soit parce que l'observation
détruit les éléments observés (cas de certains
contrôles de fabrication). (GABRIEL-R. CHEVRY, 1962).
L'objectif de l'échantillonnage est d'assurer la
représentation de la population totale à partir d'un nombre
réduit d'individus. Le choix de la taille de l'échantillon ne
doit donc pas reposer sur l'arbitraire. En effet, à chaque taille de
l'échantillon correspond des limites de confiance précises qui
qualifient le niveau de représentativité auquel on peut
valablement s'attendre.
Le théorème central limite stipule :
étant donné une population ayant une moyenne u et une variance
² , la distribution d''échantiollonnage de moyenne aura une moyenne
égale à u, une variance égale à ²/n et un
écart-type de / , la distribution d''échantiollonnage de moyenne aura une moyenne
égale à u, une variance égale à ²/n et un
écart-type de / . (NGAO Mirindi Charles, 2006). . (NGAO Mirindi Charles, 2006).
Pour déterminer cette différence nous partons de
l'hypothèse que lorsque cette moyenne et cet écart-type ne sont
pas connus dans la population à étudier, on applique la formule
suivante en choisissant un échantillon qui sert uniquement à
estimer les valeurs. En vue de tirer notre échantillon, nous nous
servons de la loi des grands nombres. Si nous voulons avoir une estimation qui
soit de 0.01 soit 1% de la moyenne et un niveau de confiance de 95%.
Nous savons que la forme générale des limites
est  +/- Z +/- Z . Comme nous voulons que Z . Comme nous voulons que Z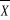 soit de 1%, la taille de l'échantantillon est obtenue en
résolvant l'équation suivante, si Z soit de 1%, la taille de l'échantantillon est obtenue en
résolvant l'équation suivante, si Z = 0.01 or le niveau de confiance que nous désirons est de 95%
c'est-à-dire une valeur de Z dans la table de 1.98 : = 0.01 or le niveau de confiance que nous désirons est de 95%
c'est-à-dire une valeur de Z dans la table de 1.98 :
1.96 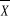 =0.01 =0.01
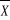 = =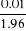 = 0.00510204 = 0.00510204
Au niveau de confiance de 95%, =5%
L'erreur-type est donc égale à 0.00510204.
Puisque le facteur de corrélation pour la population n'est pas connu, la
formule pour  est donnée par : est donnée par :
 = =  en élevant les deux membres au carré nous avons en élevant les deux membres au carré nous avons
( ) )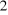 = =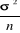 or ²= 0.05 et or ²= 0.05 et 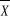 = 0.00510204 = 0.00510204
D'où n= = 96.0400373 = 96.0400373
En vertu de cette formule nous devons appliquer un
échantillon où n = 96. Mais pour rendre l'échantillon plus
représentatif, étant donné que la population est grande,
nous arrondissons n jusqu'à 120. Cette taille nous permet de
généraliser nos résultats sur le total de la population
cible.
II.4.2. Déroulement de
l'enquête
Notre enquête s'est déroulée à
partir du 30juin 2010 et a pris fin le 06 Août de la même
année. Au cours de cette période nous avons fait en plus de la
distribution du questionnaire, des multiples descentes sur terrain pour des
observations et pour interroger les agents économiques dans la ville de
Bukavu.
En ce qui concerne l'enquête, elle a consisté
à distribuer à certains ménages choisis de façon
aléatoire, le questionnaire dans les trois communes de la ville :
Bagira, Ibanda et Kadutu.
Pour répartir notre échantillon dans les trois
communes, à l'absence de la population de 2009, nous avons tenu compte
de la répartition de 2008. Cette répartition est reprise dans le
tableau suivant :
Tableau n° 5 : Répartition de la
population bukavienne en 2008
|
Communes
|
BAGIRA
|
IBANDA
|
KADUTU
|
TOTAL
|
|
Effectifs
|
92 874
|
253 856
|
272 431
|
619 161
|
|
pourcentage
|
15%
|
41%
|
44%
|
100%
|
Source : Mairie de Bukavu
Les effectifs sont répartis à raison de 15%
dans la commune de Bagira, 41% dans la commune d'Ibanda et 44% dans celle de
Kadutu. A partir de cette partition, nous pouvons répartir notre
échantillon au prorata de cette distribution. Ainsi pouvons-nous
reprendre notre échantillon dans le tableau ci-contre :
Tableau n° 6 : Répartition de
l'échantillon
|
Communes
|
BAGIRA
|
IBANDA
|
KADUTU
|
TOTAL
|
|
Nombre de ménages enquêtés
|
18
|
49
|
53
|
120
|
|
Poids dans l'échantillon en %
|
15%
|
41%
|
44%
|
100%
|
A la lumière de ce tableau, 18 ménages ont
répondu à nos questions dans la commune de Bagira, 49
ménages dans la commune d'Ibanda et 53 dans la commune de Kadutu.
II.5. Conclusion
partielle
La variation du taux de change a non seulement un impact sur
les devises mais et surtout sur la monnaie locale. L'histoire de la monnaie
congolaise est longue et a été accompagnée par plusieurs
dépréciations qui ont conduit aussi à plusieurs
réformes. Ces réformes ont permis à la monnaie congolaise
de retrouver sa place, tant soit peu, par rapport au dollar
américain.
La première monnaie congolaise (le Franc congolais),
tout juste après la colonisation, était rattaché au Franc
belge (1FC = 1FB) en 1960, mais s'est vite dépréciée et a
conduit à la réforme de 1967 qui a permis l'avènement du
Zaïre-monnaie. A son origine il coûtait plus cher que le dollar
américain auquel il fut rattaché (1Z = 2$ = 100FB). La
réforme de 1993 n'était qu'une sorte de manipulation pour se
couvrir des risques de l'inflation qui se sont généralisés
en R.D.Congo Zaïre à l'époque (1NZ = 3 000 000Z).
Par contre celle de 1998 était un déclassement définitif
du Zaïre-monnaie au profit de Franc congolais, qui a cours légal
jusqu'à présent. Pour connaître le comportement de la
population de Bukavu face à la modification des taux de change, nous
avons jugé utile d'élaborer un questionnaire d'enquête pour
les ménages. Dans l'ensemble, les questions sont subdivisées en
deux groupes permettant d'appréhender les effets de la fluctuation du
cours entre le Franc congolais et le dollar américain. Le premier groupe
se rapporte à la préférence dans la conservation des
richesses par les ménages dans la ville de Bukavu et le second concerne
le comportement de ces agents quant à la variation du taux de change.
Pour traiter les données empiriques recueillies sur
terrain, nous nous sommes servis de quelques statistiques : la moyenne
arithmétique, l'écart-type, le coefficient de variation et
l'indice de BERI (Business Environ ment Risk of investment) nous a permis de
faire calculer les indices de prix.
| 


