Memoire Online - Prédiction de durée de séjour hospitalier en gynécologie basée sur le machine learning: cas de quelques hôpitaux au sud-Kivu

Les institutions de santé et toute entreprise qui se veulent émerger cherchent sans doute à produire un travail de qualité tout en minimisant le temps et les coûts. Pour les établissements de soins, ils cherchent aussi à optimiser les fonctionnements de leurs services tout en assurant un travail de soin de qualité (on peut lire la pertinance d'une structure sanitaire à la section 1.5, page 15 ). Le système hospitalier est très complexe car il fait intervenir plusieurs catégories d'agents : les médecins, les infirmiers, les personnels administratifs et les patients. Et toutes ces catégories pourraient avoir un impact solide dans le changement de la structure hospitalière. Prédire la durée de séjour hospitalier est dans ce sens un pas d'avance pour les tructures sanitaires rêvant un épanouissement de grande envergure. La DDS est identifiée comme une variable complexe dépendant de plusieurs facteurs liés au contexte médical du patient, aux conditions de son admission et à l'organisation de l'hôpital ou du service hospitalier [19].

Dans ce chapitre, nous proposons un modèle de prédiction de la durée de séjour hospitalier en nous servant des données de certains hôpitaux de la Province du Sud-Kivu.

Ce modèle se servira des données disponibles lors de l'admission de la patiente à l'hôpital. Nous commençons d'abord par expliquer les méthodes de prédiction de la DDS, le rôle du Machine Learning dans un système hospitalier, surtout dans la prédiction de la durée de séjour, nous expliquons aussi les differents algorithmes qui ont entrainé le modèle avec un score raisonnable pour enfin finir par une conclusion et le choix d'un meilleur algorithme selon nos données.

Le milieu hospitalier est complexe, car regroupant plusieurs acteurs : d'une part, de spécialité médicale tels que les médecins, les infirmiers et les biologistes, d'autre part nous retrouvons les administratifs, les financiers et les logisticiens. Dans ce contexte institutionnel et organisationnel la définition du séjour hospitalier ainsi que la Durée De Séjour hospitalier (DDS) doit prendre en compte cette dynamique et interaction entre plusieurs acteurs [19].

Le périmètre d'étude représente dans ce sens, le secteur où la DDS sera considérée. La définition du périmètre d'étude permet d'identifier l'ensemble des facteurs qui impactent la DDS [19].

Dans le cadre de ce mémoire, le périmètre d'étude concerne l'unité médicale de Gynécologie dans quatre hôpitaux du Sud-Kivu. Dans ce sens, la Durée de Séjour Hospitalier ne sera pas calculée en fonction du nombre d'heures comme c'est le cas dans le service d'urgence ou les soins ambulatoires mais plutôt en jours. Pour nous permettre de faire une généralisation, dans le cadre de ce mémoire nous avons pris quatre structures sanitaires.

D'après la définition 1.4, la durée de séjour hospitalier étant définie comme le séjour pendant lequel un patient peut-être admis dans un ou plusieurs unités médicales. Dans le

cadre de ce travail, nous ne nous focalisons qu'à la seule unité médicale de Gynécologie. Alors, la DDS sera le temps entre l'admission de la patiente et sa sortie dans l'unité médicale de Gynécologie.

Dans la partie suivante, nous montrons les différents paramètres que nous allons utiliser dans la modélisation de la DDS.

Lors de l'admission dans une unité médicale, les données disponibles englobent les données démographiques de la patiente : son nom, son prénom, son identifiant, sa date de naissance, sa situation familiale et son adresse. Puis doivent suivre des plaintes qui l'amène à l'hopital et ainsi, de ces plaintes sortent des diagnostiques de la part des médecins. Et on chute avec une administration des médicaments.

Comme nous l'avons vu dans le chapitre 3, section 3.3.2, les informations à caratère personnel sont labélisées pour rester avec des données distrètes. Nous n'avons pas tenu conte des antécédents médicaux car nous ne les avons pas trouvées dans les tructures sanitaires concernées. La disponibilité de ces données est alors le point de départ dans le processus de prédiction.

A partir des bases de données médicales, l'historique des données est trouvée. Cette étape est suivie par une analyse des données. Ensuite, une phase de pré-traitement de données est réalisée. Elle inclut le nettoyage des données, la sélection de variables, la transformation et l'encodage des données (tout ceci dans le chapitre 3). L'ensemble de données est séparé en 2 sous-ensembles : ensemble d'apprentissage qui compte 80% des données et l'ensemble de test avec 20% de données. L'ensemble d'apprentissage sert à l'apprentissage du modèle et à la validation des résultats et l'ensemble de test pour l'évaluation des résultats obtenus.

Cette section concerne les résultats obtenus suite à l'implémentation des différents processus pour l'apprentissage automatique décrits dans le chapitre 2 et le chapitre 3. Les résultats ici présentés sont issus des données des algorithmes de regression.

4.3.1 Le réseau de neurone dans la prédiction de Durée de Séjour Hospitalier

En prédisant par l'algorithme des réseaux de neurones (Neural Network), nous avons trouvé par rapport à nos données que la prédiction a un score négatif, soit de 78% pris négativement pour les données de test et 97,6% pour les données d'apprentissage. La figure suivante (figure 4.1) est une représentation des valeurs prédites contre les valeurs réelles.

FIGURE 4.1 - Valeurs actuelles contre les valeurs prédites en utilisant le réseau de neurone

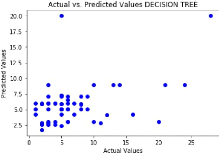
4.3.2 Les arbres de décision dans la prédiction de Durée de Séjour Hospitalier

Dans la prédiction de la DDS par la méthode des arbres de decision (decision Tree), le score pour ce modèle est positif et il est évalué à 0.13.

FIGURE 4.2 - Valeurs actuelles contre les valeurs prédites en utilisant les arbres de décision

Nous avons une DDS des données de comptage, ce qui nous permet d'affirmer que nous pouvons utiliser deux distributions : soit la distribution Binomiale ou la distribution de poisson. Dans cette partie, nous allons examiner les deux distributions et tirer une meilleure conclusion.

Ce modèle a été utilisé avec la distribution de poisson et vous avons été satisfait de son score qui est de 97%. Nous nous sommes rendu compte que c'est le vrai dans la prédiction telle que celle ci.

Le resumé du modèle linéaire généralisé est présenté dans le tableau 4.1.

La deuxième colonne du tableau indique les coéfficients du MLG. Etant donné que la confiance du modèle est d'à peu près 97%, le p - value est donc de 0.03. Certains coéfficients sont statistiquement significatifs car, ayant un p - value inférieur à 0.03. Comme c'est le cas par exemple de Adresse, l'âge, la grossesse, lers Inféctions Urinaires, les avortements, les Anti Inféctieux, les Analgésiques, les Vitamines, les céphalo, autres et la moyenne de DDS par hopital. D'après l'équation 2.4, page 30 la DDS prédite est supposée être ij, et la fonction de lien dans ce modèle est la fonction logarithme néperien

Tableau 4.1 - Résumé du modèle linéaire généralisé avec la distribution de poisson

Covariance Type	: coef	nonrobust std err	z	P>\|z\|	[0.025	0.975]
Adresse(km)	-0.0899	0.029	-3.106	0.002	-0.147	-0.033
Age	0.1283	0.028	4.644	0.000	0.074	0.182
Hopital	-0.0342	0.034	-1.008	0.314	-0.101	0.032
Grossesse	0.3048	0.083	3.686	0.000	0.143	0.467
IU	-0.2051	0.089	-2.299	0.022	-0.380	-0.030
MAV	-0.1270	0.085	-1.496	0.135	-0.293	0.039
Anémie	-0.0498	0.082	-0.608	0.543	-0.210	0.111
Paludisme	0.1256	0.093	1.353	0.176	-0.056	0.308
Avortement	-0.4229	0.077	-5.518	0.000	-0.573	-0.273
Infections	0.0844	0.079	1.063	0.288	-0.071	0.240
Autres	0.0872	0.065	1.333	0.183	-0.041	0.215
AB	-0.0349	0.068	-0.514	0.607	-0.168	0.098
AP	-0.0680	0.103	-0.661	0.509	-0.270	0.134
OCYTOCIQUES	-0.0971	0.079	-1.234	0.217	-0.251	0.057
AI	-0.5020	0.235	-2.136	0.033	-0.963	-0.041
ASM	0.0689	0.067	1.024	0.306	-0.063	0.201
ANAL	-0.2039	0.110	-1.856	0.064	-0.419	0.011
AAL	0.3220	0.090	3.598	0.000	0.147	0.497
Vitamine	0.5866	0.133	4.403	0.000	0.326	0.848
Cephalo	0.3184	0.096	3.318	0.001	0.130	0.506
AA	-0.0572	0.130	-0.438	0.661	-0.313	0.199
Transfusion	0.2113	0.169	1.248	0.212	-0.121	0.543
Autre2	0.1285	0.059	2.190	0.028	0.014	0.244
MeanDDSHop	0.2852	0.025	11.414	0.000	0.236	0.334

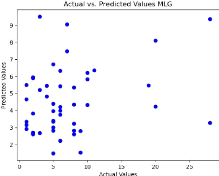
FIGURE 4.3 - Valeurs actuelles contre les valeurs prédites en utilisant le modèle linéaire généralisé avec la distribution de poisson

('q = log(i)). Avec ,u la moyenne de la durée de séjour. L'équation 2.4 devient donc :

En guide de l'équation 4.1, en utilisant les variables significatives telles que trouvées dans le tableau 4.1, la DDS 'q sera :

- 'q est multipliée par ^e-0.0899lorsque la variable Adresse est augmentée d'une unité. La valeur ^e-0.0899E]0, 1[, la DDS va donc diminuer

- 'q est multipliée par ^e0.1283lorsque la variable Age est augmentée d'une unité. La quantité ^e-0.1283est supérieure à 1, ce qui signifie que plus l'âge augmente, la DDS aussi augmente.

- 'q est multipliée par ^e0.2852lorsque la variable Durée Moyenne de DDS est augmentée d'une unité. La quantité ^e0.2852est supérieure à 1, ce qui signifie que plus l'âge augmente, la DDS aussi augmente.

- pour les variables dichotomiques, on ne fait pas trop de commentaires car on constate qu'elles ne prendrons pas des valeurs au délà de 0 et 1.

On peut donc voir qu'il y a des variables significatives à coéfficients positifs ont tendences à augmenter la DDS d'un patient à l'Hopital.

Par rapport aux données prédites par ce modèle, la variance est de 6.549 et la moyenne est de 5.867. Ceci nous montre que, la différence sur ces deux est d'environs 1.364, où il

Pour cette distribution, nous avons un degré de confiance de 95%. Le tableau 4.2 nous présente le résumé de ce modèle. L'interprétation des coéfficients de ce tableau utilise la même procédure que pour le tableau 4.1. Par contre, nous n'avons qu'une seule variable significative qui est la durée moyenne de DDS par Hopital. Cette variable lorsqu'elle augmente d'une unité, la DDS est multipliée par un facteur de e0.3064.

D'après les analyses des tableaux 4.1 et 4.2 et comme nous avons deux modèles différents, nous allons comparer leurs prédictions par la méthode AIC (Akaike Information Criterion ) de python où le AIC des modèles linéaires généralisés en utilisant respectivement les distributions de poisson et binomiale négative sont : 1569 et 1578.

Il s'en suit donc que la distribution de poisson est celle qui est plus adaptée (car ayant le plus petit AIC) à ces données que l'autre. Ceci était déjà visible par le biais de la signification des variables.

Dans le cadre de cette étude, le modèle des k plus proches voisins a prédit avec un score approximatif qui est de 0.09 soit moins de 10%. La figure 4.4 est une représentation des valeurs prédites contres les séjours réels des malades.

FIGURE 4.4 - Valeurs actuelles contre les valeurs prédites en utilisant le k Plus proches voisins

Tableau 4.2 - Résumé du modèle linéaire généralisé avec la distribution binomiale négative

Covariance Type	: coef	nonrobust std err	z	P>\|z\|	[0.025	0.975]
Adresse(km)	0.0155	0.074	0.210	0.834	-0.129	0.160
Age	0.0509	0.070	0.722	0.470	-0.087	0.189
Hopital	-0.0045	0.079	-0.056	0.955	-0.160	0.151
Grossesse	0.0667	0.191	0.349	0.727	-0.308	0.441
IU	-0.0739	0.208	-0.355	0.723	-0.482	0.334
MAV	-0.1880	0.212	-0.887	0.375	-0.604	0.228
Anémie	-0.1224	0.194	-0.632	0.527	-0.502	0.257
Paludisme	-0.0099	0.229	-0.043	0.965	-0.458	0.438
Avortement	-0.3523	0.183	-1.930	0.054	-0.710	0.005
Infections	-0.1126	0.204	-0.551	0.581	-0.513	0.288
Autres	0.0388	0.168	0.230	0.818	-0.291	0.369
AB	-0.0008	0.171	-0.005	0.996	-0.335	0.334
AP	0.0533	0.227	0.235	0.814	-0.391	0.498
OCYTOCIQUES	-0.0898	0.191	-0.470	0.639	-0.464	0.285
AI	-0.5137	0.540	-0.951	0.341	-1.572	0.545
ASM	0.2355	0.178	1.321	0.186	-0.114	0.585
ANAL	-0.0299	0.232	-0.129	0.898	-0.485	0.425
AAL	0.0568	0.252	0.226	0.821	-0.436	0.550
Vitamine	0.4917	0.385	1.276	0.202	-0.263	1.247
Cephalo	0.1706	0.279	0.612	0.541	-0.376	0.717
AA	0.0415	0.313	0.133	0.894	-0.572	0.655
Transfusion	0.0846	0.316	0.268	0.789	-0.534	0.704
Autre2	0.0038	0.141	0.027	0.978	-0.272	0.280
MeanDDSHop	0.3064	0.061	5.026	0.000	0.187	0.426

Nous avons déjà vu d'après les trois sous-sections précédentes les deux algorithmes de l'apprentissage supervisé en regression que nous avons utilisé sur nos données. Le tableau suivant reprend pour chacun des modèles le score, le F1-score, etc.

Tableau 4.3 - Évaluation du modèle statique de prédiction de DDS : régression

D'après le tableau 4.3, le modèle linéiare généralisé est celui qui approxime la durée de séjour hospitalier en minimisant les erreurs.

Ce chapitre étant concentré sur la modélisation de la prédiction de la durée de séjour hospitalier, nous sommes parti des bases de données décrites dans le chapitre 3, pour faire une prédiction de la DDS. Les méthodes de prédiction de la DDS au moment de l'admission de la patiente sont basées sur des fouilles des données. Nous avons trouvé que le modèle linéaire généralisé est le modèle très fidele dans la prédiction d'un quelconque séjour hospitalier.

Prédiction de durée de séjour hospitalier en gynécologie basée sur le machine learning: cas de quelques hôpitaux au sud-Kivu

Chapitre 4