Section 2.
Méthodologie et données.
Dans la section précédente, nous
avons présenté les faits stylés concernant
l'évolution des concepts de notre étude. En nous basons sur cette
analyse descriptive en fonction des données détenues et de la
littérature empirique nous allons d'abord présenter les
modèles et les variables utilisées (2.1), enfin la méthode
d'estimation adéquate et les sources de données (2.2).
2.18. 2.1.
Présentation des modèles
Certains auteurs ont utilisé le
modèle des données de panel dynamique pour mesurer la relation le
capital humain et la transformation structurelle. En nous
référant aux travaux d'Arawomo (2014), alaya et al.(2012) qui
ont expliqué la transformation structurelle à travers la
diversification et la sophistication des exportations, nous adoptons une
modélisation en données de panel dynamique pour ces deux
équations. La première équation va nous permettre de
tester l'impact du capital humain sur la diversification des exportations d'ASS
et la seconde, tester l'influence du capital humain sur la sophistication des
exportations. Etant donné que nous avons deux dimensions qui mesurent la
transformation structurelle notamment la diversification et la sophistication,
de ce fait les deux modèles se spécifient initialement
d'après ces auteurs comme suit:
Ainsi, nous avons les spécifications
suivantes :
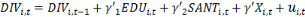 Ø Ø 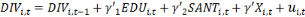 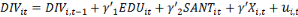 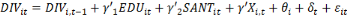 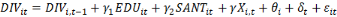 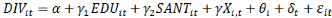 (1) (1)
i= (1,..........22) et t=(1,........17)
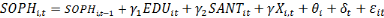 Ø Ø 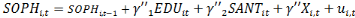 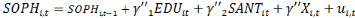 (2) (2)
i= (1,..........22) et t = (1,........17)
Ø 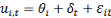 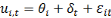 (3)
(3)
Avec 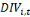 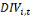 et et 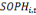 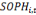 qui représentent les deux mesures de la transformation
structurelle des pays i à la période t. qui représentent les deux mesures de la transformation
structurelle des pays i à la période t.
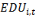
et 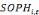 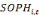 représentent les vecteurs des indicateurs de l'éducation
et de la santé qui constituent les variables d'intérêt et
utilisées comme mesures du capital humain pour les pays i à la
période t. X est le vecteur des autres variables de contrôle
susceptibles d'expliquer la diversification et la sophistication des
exportations. représentent les vecteurs des indicateurs de l'éducation
et de la santé qui constituent les variables d'intérêt et
utilisées comme mesures du capital humain pour les pays i à la
période t. X est le vecteur des autres variables de contrôle
susceptibles d'expliquer la diversification et la sophistication des
exportations.
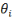 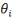 , l'effet fixe-pays (prenant en compte la dimension individuelle), , l'effet fixe-pays (prenant en compte la dimension individuelle), 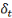 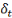 l'effet fixe-temps et l'effet fixe-temps et 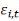 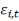 le terme d'erreur. le terme d'erreur.
Partant de cette spécification, notre
modèle intègre d'autres variables afin de prendre en compte
l'influence des autres facteurs sur la transformation structurelle. Nos
modèles spécifiés sont les suivant :
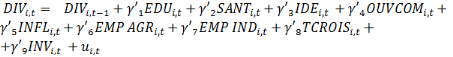 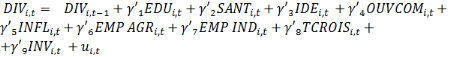 (4) (4)
ET
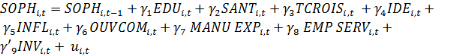 (5) (5)
A priori il ne sera pas question ici de faire
recours à des équations simultanées, nous allons estimer
nos deux équations indépendamment l'une de l'autre. En effet, ces
équations peuvent être estimées par les (MCO, DMC, TMC),
mais le problème d'endogéneité peut faire en sorte que les
variables et résidus de l'équation peuvent être
corrélés. Alors le plus pertinent est dans la résolution
est de recourir à des techniques plus élaborées de
variables instrumentales pour tenter de corriger le biais dit
d'endogéneité.
| 


