III.3.6. Neurone formel
Un neurone formel est un automate très simple imitant
grossièrement la structure et le fonctionnement d'un neurone biologique.
La première version de ce dernier est celle de Mc Culloch et W. Pitts et
date de 1943. S'inspirant de leurs travaux sur les neurones biologiques, ils
ont proposé le modèle du neurone formel qui se voit comme un
opérateur effectuant une somme pondérée de ses
entrées suivie d'une fonction d'activation (ou de transfert) comme
indiqué par la figure suivante.
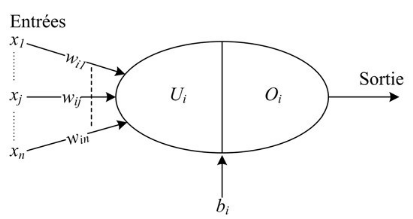
Figure 3.20: Neurone
formel.
Y=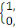 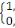 si si 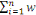 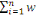 ixi ixi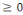 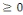
Si non Ui
Représente la somme pondérée des
entrées du neurone
???? = ? ?????????? + ????
Où :
????????????é????????????'????????é??????o??????????é????????????????????????????????????????????????????????????????????????
????????é??????????????????????????????????????????????????????????????????'????????é????????????????????????
????= ??(????)
????????????????????????????????????????????????????????????????????'????????????????????
III.3.7. Sortes de réseau de neurones
Les types de réseau de neurones différent par
plusieurs paramètres :
· La topologie des connexions entre les neurones, on
distingue deux types de réseau neuronaux : le réseau de neurone
bouclé et non bouclé
· La fonction d'agrégation utilisée (somme
pondérée, distance pseudo euclidienne, indice d'agrégation
de Ward,)
· La fonction de seuillage utilisée
(sigmoïde, échelon, fonction gaussienne, ...)
· L'algorithme d'apprentissage (rétro
propagation du gradient, cascade corrélation...)
· Méthodes de dégradation des
pondérations (weightdecay), permettant d'éviter les effets de
bord et de neutraliser le sur-apprentissage.
· Types d'apprentissage : apprentissage supervisé,
non supervisé ou apprentissage par renforcement.
III.3.8. Topologie d'un réseau de neurones
III.3.8.1. Perceptron et son fonctionnement
Avant d'aborder le comportement collectif d'un ensemble de
neurones, nous allons présenter le perceptron (un seul neurone) en phase
d'utilisation. L'apprentissage ayant été réalisé,
les poids sont fixes. Le neurone de la figure 1.12 réalise une simple
somme pondérée de ces entrées, compare une valeur de
seuil, et fourni une réponse binaire en sortie.
Les connexions des deux entrées e1 et e2 au neurone
sont pondérées par les poids w1 et w2. La valeur de sortie du
neurone est notée x. Elle est obtenue après somme
pondérée des entrées (a) et comparaison à une
valeur de seuil S.
Dans le cadre de ce travail, nous pouvons interpréter
le résultat de la manière suivante :
· La transaction sera frauduleuse si la valeur de x est 0
· La transaction sera normale si la valeur de x est +1.
| 


