III.1.4. Concepts de base
de Fouille de données
III.1.4.1. Matrice des données - Individu -
Variable
Nous représentons les données sous la forme
d'une matrice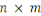 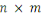 , avec , avec   lignes et lignes et 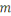 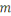 colonnes, les lignes correspondant aux entités de l'ensemble de
données (entrepôt de données, base de données,
tableur, etc.)) et des colonnes représentant des attributs ou
propriétés appelées variables. Chaque ligne de la matrice
de données enregistre les valeurs d'attribut observées pour une
entité donnée qu'on appelle individu ou instance ou encore
exemple. Cette matrice est donnée par : colonnes, les lignes correspondant aux entités de l'ensemble de
données (entrepôt de données, base de données,
tableur, etc.)) et des colonnes représentant des attributs ou
propriétés appelées variables. Chaque ligne de la matrice
de données enregistre les valeurs d'attribut observées pour une
entité donnée qu'on appelle individu ou instance ou encore
exemple. Cette matrice est donnée par :
|
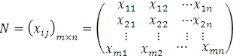 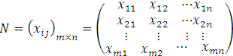 , ,
|
|
où 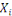 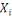 désigne la désigne la   -ème ligne, qui est un n-tuple donné par -ème ligne, qui est un n-tuple donné par
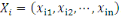
Le nombre d'individus   est appelé la taille des données, alors que le
nombre de variables est appelé la taille des données, alors que le
nombre de variables 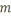 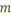 est appelé la dimension des données. est appelé la dimension des données.
Une variable qualitative est une variable pour laquelle la
valeur mesurée sur chaque individu ne représente pas une
quantité. Les différentes valeurs que peut prendre cette variable
sont appelées les catégories, modalités ou niveaux.
Une variable est quantitative si elle reflète une
notion de grandeur, c'est-à-dire si les valeurs qu'elle peut prendre
sont des nombres pouvant être classés en utilisant la relation
=.
III.1.4.2. Ressemblance
Une ressemblance (ou proximité) est un
opérateur capable d'évaluer précisément les
ressemblances ou les dissemblances qui existent entre ces données. Cet
opérateur permet alors de mesurer le lien entre les individus d'un
même ensemble.
III.1.4.3. Dissimilarité
Un opérateur de ressemblance 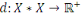 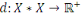 défini sur l'ensemble d'individus défini sur l'ensemble d'individus
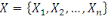 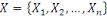 est dit indice de dissimilarité (ou dissimilarité),
si et seulement vérifie les propriétés
suivantes : est dit indice de dissimilarité (ou dissimilarité),
si et seulement vérifie les propriétés
suivantes :
|
(P1)
|
|
(Symétrie)
|
|
(P2)
|
|
(Positivité)
|
III.1.4.4. Distance
Un opérateur de ressemblance 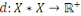 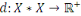 défini sur l'ensemble d'individus défini sur l'ensemble d'individus
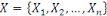 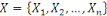 est dit distance ou métrique, si et seulement, en plus de
propriétés (P1) et (P2), il vérifie les
propriétés suivantes : est dit distance ou métrique, si et seulement, en plus de
propriétés (P1) et (P2), il vérifie les
propriétés suivantes :
|
(P3)
|
|
(Identité)
|
|
(P4)
|
|
(Positivité)
|
La distance la plus utilisée pour les données de
type quantitatives continues ou discrètes est la distance de Minkowski
d'ordre á définie dans 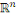 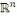 par : par :
où 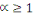 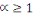 . .
En particulier si :
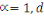 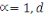 est la distance de city-block ou Manhattan. est la distance de city-block ou Manhattan.
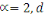 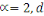 est la distance Euclidienne classique. est la distance Euclidienne classique.
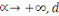 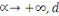 est la distance de Tchebychev définie comme suit : est la distance de Tchebychev définie comme suit :
NOTA
Dans la pratique, c'est la distance euclidienne qui est le
plus souvent utilisée, mais la distance de Manhattan est aussi parfois
utilisée, notamment pour l'atténuement de l'effet de larges
différences dues aux points atypiques ou aberrants pour la simple raison
que puisque leurs coordonnées ne sont pas élevées au
carré.
| 


