PARTIE III : RÉSULTATS ET DISCUSSION
22
Résultats
III.1. Résultats
III.1.1. Nature et intensité de l'aléa
inondation
III.1.1.1. La nature de l'aléa inondation
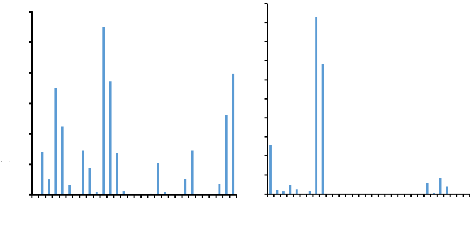
La figure 5 montre les hauteurs de pluies survenues sur le
bassin versant du fleuve San-Pedro durant les mois de juin et juillet 2017.
Pendant le mois de juin, il pleut pratiquement tous les jours, les hauteurs de
pluies qui en découlent sont très importantes. Le mois de juin
enregistre une hauteur maximale de 115 mm et celle de juillet est de 93 mm. Ces
grandes quantités d'eau (115 à 95 mm) qu'apportent ces pluies en
moins de 24 H saturent rapidement le sol compte tenue de la
perméabilité aussi élevée sur le bassin versant. La
saturation rapide du sol génère des ruissellements qui entrainent
des inondations sur le bassin versant du fleuve San-Pedro. Ces
précipitations que connait le bassin versant du fleuve San-Pedro sont
qualifiées de pluies extrêmes. Elles sont violentes, le seuil
critique est atteint en quelques heures et provoques de graves
dégâts.
Mois de juillet 2017
Mois de juin 2017
100
90
80
70
60
50
40
30
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
120
100
80
60
40
20
hauteurs de pluies (mm)
0
20
10
0
Figure 5 : Hauteur de pluie des mois de juin et juillet 2017 de
la station de pompage de San-Pedro
III.1.1.2. Intensité de l'aléa inondation
sur le bassin versant du fleuve San-Pedro La figure 6 montre les
résultats du critère de comparaison graphique. Il en
résulte que la loi de Weibull (W2, B), présente l'avantage
d'être un modèle simple de cette station dont les maximums des
valeurs des débits annuels sont bien corrélés à
ladite loi. Elle met en évidence un bon comportement comparé aux
lois GEV, Gumbel et la loi Normal.
23
Résultats
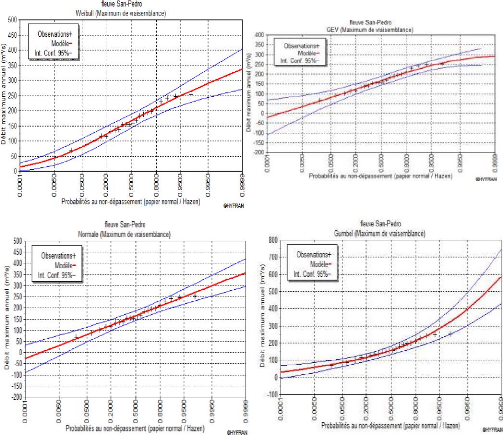
Figure 6: Graphes des différentes lois de comparaison
ajustés par la méthode du maximum de vraisemblance aux
séries de débits moyens annuels de la station de pompage de
San-Pedro
24
Résultats
Les critères d'information Akaike et Bayésien
(AIC et BIC) permettent de retenir la loi de Weibull (Tableau I). Cette loi est
arrivée en tête parmi toutes les lois mises en compétition
avec la plus grande probabilité à posteriori P (Mi/X)= 67,14 et
les plus faibles valeurs de critères de AIC et BIC qui sont
respectivement de 526,70 et 530,02. La loi de Gumbel vient en deuxième
position avec une probabilité à postériori P (Mi/X) =
21,2, des valeurs de critères de AIC (529,01) et BIC (533,52). La loi de
GEV vient en troisième position avec une valeur de probabilité
à postériori P (Mi/X) = 11,67 et des valeurs AIC (528,53) et BIC
(533,52) plus élevées.
Tableau I : Comparaison des lois statistiques pour
l'ajustement des différents modules
|
Modèle
|
Nb. de
|
Débit
|
P(Mi)
|
P (Mi/x)
|
BIC
|
AIC
|
|
Paramètre
|
(m3/s)
|
|
|
|
|
|
Weibull (Maximum de vraisemblance)
|
2
|
962,97
|
33,33
|
67,14
|
530,02
|
526,70
|
|
Gumbel (Maximum
de vraisemblance)
|
2
|
1202,09
|
33,33
|
21,2
|
532,33
|
529,01
|
|
GEV (Maximum de
vraisemblance)
|
3
|
935,14
|
33,33
|
11,67
|
533,52
|
528,53
|
Les quantiles de crue pour divers périodes de retour
sont consignés dans le tableau II. On remarque que les résultats
estimés par les différentes lois sont très peu variables
d'une période de retour à une autre. Cependant on observe une
variation importante des débits estimés par la loi de Gumbel pour
les périodes de retour de 2, 20, 50 et 100 ans avec des débits
respectifs de 441, 806, 900 et 963 m3/s.
Tableau II : Débits des différentes périodes
de retour en fonction des lois
|
Période de
retour (ans)
|
Probabilité au
non
dépassement
|
GEV
m3/s
|
GUMBELL
m3/s
|
WEIBULL
m3/s
|
|
2
|
0,5
|
445
|
424
|
441
|
|
20
|
0,95
|
795
|
903
|
806
|
|
50
|
0,98
|
881
|
1070
|
900
|
|
100
|
0,99
|
935
|
1200
|
963
|
25
Résultats
| 


