Cartographie des zones inondables sur le bassin versant du fleuve San-Pedro( sud-ouest de la côte d'Ivoire).

II.2.2.2. 2.Cas du régime non permanent

Les équations se présentent comme suit :

? Equation de la conservation de la masse :

En supposant que le flux est incompressible, la forme différentielle instable de l'équation de

conservation de masse (continuité) est :

(Eq.7)

Où : t : temps, u et v : composantes de vitesse dans les directions x et y respectivement et q est un terme de flux tributaire. Sous forme vectorielle, l'équation de continuité prend la forme :

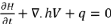
(Eq.8)

.

Où :

V= (u, v) est le vecteur vitesse et l'opérateur différentiel

(?) : est le vecteur des opérateurs dérivés partiels donnés par

? Equation des moments

(Eq.9) (Eq.10)

17

Où : u et v : vitesses dans les directions cartésiennes, : accélération gravitationnelle ;

vt : coefficient de viscosité tourbillonnaire horizontale cf : coefficient de frottement du fond

f : paramètre de Coriolis

II.2.2.3. Calage et validation

Le calage et la validation ont pour but d'ajuster les paramètres du modèle de façon à ce que l'adéquation entre les débits simulés et observés soit maximale. La méthodologie consiste à subdiviser la période d'observation de chaque bassin versant en sous- périodes avec calage sur une période et validation sur le reste des observations et vice- versa. Toutefois, il faut réserver une période de mise en route. Cette action est répétée de façon à caler successivement sur toutes les sous périodes et à valider sur celles correspondantes. Le calage et la validation du modèle

18

Matériel et méthodes

Hec-ras ont été réalisés respectivement sur les périodes 2003 et 2004 avec une année de mise en route pour chaque étape de la modélisation.

Les périodes retenues sont celles qui ont données de meilleures performances de simulation des écoulements avec le modèle Hec-ras.

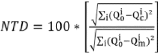
Ces deux modèles (calage et validation) seront soumis à un critère d'optimisation appelé le coefficient de Nash ; le coefficient de Nash permet de juger de la qualité de l'ajustement et de faciliter la comparaison des ajustements sur différents bassins dont les écoulements ont des ordres de grandeur différents (Nash & Sutcliffe, 1970). Le critère de Nash s'exprime comme suit : (Eq.11)

Où :

Qci et Qⁱo sont respectivement les débits calculés et observés au jour i ;

Q_c et Q_o sont les moyennes respectives de Qci et Qⁱo sur les n jours servant au calcul du coefficient.