4.2.4. CALCUL DES MOMENTS
4.2.4.1 POIDS PROPRES
4.2.4.1.1 POUTRE
Profilé IPE 500 : A = 11600 mm ; e = 18 cm et h = 500
mm
P = h e A = 25000 0,18 0,5 78500 0,0116
= 3160,5 N/m
4.2.4.1.2 ENTRETOISE
H = 500 mm et = 200 mm
H = 360 mm et = 170 mm
L = 10 m ; l = 24 m et l = 2 m
P = = , , = 960,84
P = p p = 0,31605 0,096 = 0,412
4.2.4.2 SURCHARGE FIXE (p') POUR 1/2 PONT
? Garde-corps : 1 KN/m = 0,01 t/m ? Tablette : 0,3 0,15 2,5 =
0,1125
? Trottoir :
- pierre de taille : 0,15 * 0,15 * 2,3 = 0,0518 t/m - sable : 0,1
* 2 * 1,8 = 0,36 t/m
67
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
68
TRAVAIL DE FIN D'ETUDE
- Dallette : 0,05 * 2 * 2,2 = 0,22 t/m
- couche de roulement : 0,05 * 1 * 2,3 = 0,115 t/m
- couche de forme en béton : 0,04 * 1 * 2,3 = 0,092
t/m
- couche d'isolation : 0,03 * 1 * 2,2 = 0,066 t/m
- bac en acier : 0,01 * 1 * 7,8 = 0,078 t/m
La somme donne : 1,1053 t/m
Pour 1/2 pont, nous avons 5,5 poutres, on a :
P` = , , = 0,2 t m
P P' = 0,412 0,2 = 0,612 t m ? CALCUL DES
CONTRAINTES
= avec M = P * d
P : charge unitaire
d : Distance entre P et l'axe du pont Ù : aire totale
I : moment d'inertie

Figure 43 : Calcul des contraintes
Avec : d = 10 m ; d = 8 m; d = 6 m; d = 4 m; d = 2 m et d = 0
Nous avons une section unitaire pour chaque poutre : W = 1
Avec 11 poutres : W = à = W = 1 m
L'aire totale : Ù = ? W = 1 11 =
11 m
68
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
|
I = I =
|
I = W
I = W
|
d
d
|
= 1
= 1
|
10 8
|
69
TRAVAIL DE FIN D'ETUDE
= 100 m = 64 m
|
|
I =
I =
I =
|
I = W
I = W
I = W
|
d d
d
|
= 1
= 1
= 1
|
6
4
2
|
= 36 m = 16 m = 4 m
|
|
I = W d
|
=
|
1
|
0 = 0
|
|
|
I = 2 (I I
M = P * d =
|
I
1 *
|
10
|
I I ) =
= 10 tm
|
440 m
|
- Si P = 1t ; au milieu du pont, donc le coefficient de
répartition des charges est
:C = = 0,09 t car chaque poutre sera chargée
identiquement
- Si P = 1 t est placé à l'appui 1 du pont, on a
une rotation de la section autour de 0, l'axe de la coupe transversale
Ainsi on a à
Tableau N°8 : calcul des contraintes
|
|
|
|
|
_
|
|
|
|
|
=
|
|
0,317
=
|
1
|
|
=
|
0,044
|
|
2
|
|
|
|
/
|
6$
|
1
|
1
|
|
0
|
|
=
|
|
0,2/ 1
=
|
=
|
--
|
=
|
|
|
|
|
=
|
|
|
|
=
|
|
|
|
|
|
0,226
=
|
|
44
|
=
|
0,046
|
|
6
|
|
=
|
|
|
|
=
|
|
|
|
|
0,18
=
--
|
|
=
|
0,0918
|
|
|
|
|
=
|
|
|
|
=
|
|
|
|
|
0,135
=
|
|
=
|
0,137
|
|
|
|
|
6
|
=
|
0
|
|
|
|
|
|
|
|
440
|
0,09
=
|
|
P = W
69
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
70
TRAVAIL DE FIN D'ETUDE
Tableau N°9 : calcul des forces
|
P = 1 * 0,317 = 0,317 t
|
P =
|
|
1 * 0,044
= 0,044 t
|
|
P = 1 * 0,271 = 0,271 t
|
P =
|
1 * 0
|
= 0 t
|
|
P = 1 * 0,226 = 0,226 t
|
P = 1
|
* (-
|
0,046) = - 0,046 t
|
|
P = 1 * 0,18 = 0,18 t
|
P =
|
1 *
|
(-
|
0,0918) = - 0,0918 t
|
|
P = 1 * 0,135 = 0,135 t
|
P =
|
1 *
|
(-
|
0,137) = - 0,137 t
|
|
P = 1 * 0,09 = 0,09 t
|
|
|
|
|
|
? P = 0,9882 t 1 t
|
|
|
|
|
? REPARTITION TRANSVERSALE DES CHARGES

Figure 44 : Répartition transversale des
charges
Tableau N°10 : calcul des surfaces
|
Ligne
d'influence
|
Valeur des surfaces des diagrammes (m )
|
|
S = (0,43 * 15)/2
|
S = (0,19 * 8)/2
|
|
|
1 et 11
|
= 3,225
|
= 0,76
|
S = 2,465
|
|
2 et 10
|
S = (16 ,7 * 0,31)/2
|
S = (7 * 0,14)/2
|
S = 2,1
|
|
= 2,59
|
= 0,49
|
|
70
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
71
TRAVAIL DE FIN D'ETUDE
|
3 et 9
|
S = (18 * 0,26)/2
|
S = (5,5 * 0,08)/2
|
S = 2,12
|
|
= 2,34
|
= 0,22
|
|
|
4 et 8
|
S = (20 ,8 * 0,2)/2
|
S = 0
|
S = 2,08
|
|
= 2,08
|
|
|
|
5 et 7
|
S =
|
S = 0
|
S = 2,04
|
|
(0,02 + 0,15)*24 /2
|
|
|
|
= 2,04
|
|
|
|
6
|
S =
|
S = 0
|
S = 2,16
|
|
(0,09 + 0,09)*24 /2
|
|
|
|
= 2,16
|
|
|
? LA SURCHARGE DE LA FOULE
Q = 5 KN/m 1,5 = 7,5 = 0,75 t m
4.2.4.2 FOULE
-
-
|
q (charge positive) :
|
0,75 *
|
S =
|
0,75 *
|
3,225
|
= 2,4 t/m
|
|
q (charge negative) :
|
0,75 *
|
S =
|
0,75 *
|
0,76
|
= 0,57 t/m
|
? CHARGE DE LA POUTRE LONGITUDINALE LA PLUS
CHARGEE
? CALCUL DES SURFACES DES LIGNES D'INFLUENCE DE MOMENT
Soit la poutre principale divisée en 10 parties
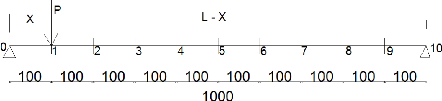
Figure 45 : Calcul des surfaces des lignes d'influence de
moment
M =
avec X' = L - X ? M = (L X)X
71
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
72
TRAVAIL DE FIN D'ETUDE
Tableau N°11 : calcul des moments
|
M = M =
|
0
|
|
M = M = (1
|
* 3 * 7)/10
|
= 2,1 tm
|
|
= =
|
|
0,9 tm
=
|
= =
|
=
|
|
|
M M
|
|
|
M M
|
2,4 tm
|
|
= =
|
|
1,6 tm
=
|
1 5 5
|
= 2,5
|
|
|
M M
|
|
|
|
M
= 10
|
|
|



