V.1.3.1. Détermination des niveaux de projet :
i' Le Niveau 0 (N0) : c'est le niveau des
tâches n'ayant pas de prédécesseurs ou encore niveau des
tâches non soumises à des contraintes d'antériorités
;
i' Le Niveau Z (NZ) : c'est le niveau de la
dernière tâche de la réalisation du projet ;
i' Le Niveau 1 : pour l'obtenir, on doit
rayer dans le tableau précédent toutes tâches de N0de la
colonne P(x). Les tâches x correspondant aux lignes P(x)
entièrement rayées sont du niveau 1.
Même procédure pour les autres niveaux et on aura
pour notre projet les niveaux des tâches suivants :
i' N0={A} ; i' N4={F} ;
i' N1={B} ; i' N5={G} ;
i' N2={C} ; i' Nz={H}.
i' N3={D, E} ;
Page 70 sur 95
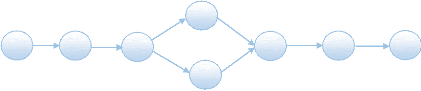
V.1.4. Elaboration du graphe PERT
Un graphe permet de visualiser le chemin critique
c'est-à-dire le chemin conduisant du début à la fin du
projet et dont toute variation de durée d'une de ses tâches
(tâches critiques) peut bouleverser la durée de réalisation
du projet.
Il a pour but de décrire graphiquement les contraintes
d'antériorités liant les tâches à exécuter
pour la réalisation de ce projet et sa construction exige que les
sommets soient placés de gauche à droite en fonction de leur
niveau. Ainsi, voici le graphe PERT pour notre projet :
D
A B
C
F G H
E
Figure 30.Le Graphe PERT
| 


