TestdedépendancechoisiiciestletestdeCHI2:
Y=CO2 (émissionen kt) X = commerce (en part du PIB)H0:X
etYsontindépendantes
H1:XetYsontdépendantes
Pour éviter d'avoir un trop grand tableau (60 lignes x
60 colonnes), j'ai modifié le tableau
decontingenceafindelecouperen4classes.CelanouspermettradepouvoirfaireuntestdeCHI2.
Seuil de significativité ( l'erreur de premier
espèce) est la probabilité de rejeter H0 alors qu'elle
estvraie.Nous allons choisir ici deprendreun seuil à5%.
On va déterminer notre d qui va nous permettre de poser
la règle de décision, le d max va se liredanslatablestatistiquedu
CHI2.
LorsquedserainférieuràdmaxalorsonvaaccepterH0etsidestsupérieuràdmaxalorsonpourrarejeter
H0.
Tableau12enannexe:
d= 127,2625
Pour obtenir d max je vais regarder le tableau du CHI2, le
degré de liberté est de 9 ici et notre
seuildesignificativitéestde5%,d maxest doncégalà16,92dans
letableau.
Icidestsupérieuràdmax,donconrejettel'hypothèseH0quiditquelesvariablessontindépendantes.
Cependant , on ne peut pas en être certain à 100% car nous avons
ici une erreur depremièreespècecar on
peuts'êtretrompé.
Toutefois, le test de CHI2 nous donne des preuves statistiques
qui sont beaucoup plus forte que lasimplecorrélation.
Icilapvaleurestégalà0,000,celle-civanouspermettredeconclurelorsquel'onnevapassoumettre
un test, elle va nous permettre de conclure sans passer par la lecture de la
table du
CHI2.Lorsquelapvaleurestsupérieurà5%,j'accepteH0etlorsqu'elleestinférieurà5%alorsjerejetteH0.
Jevaisdoncrejeter monH0car lapvaleur estde0.
Cequirenforceencoreunefoislefaitqu'ilyabienunlienentrelecommercedelaChineetlesémissionsdeCO2
dans lepays.
Toutesles commandes effectuées sur
StatasontreportéesenAnnexe.
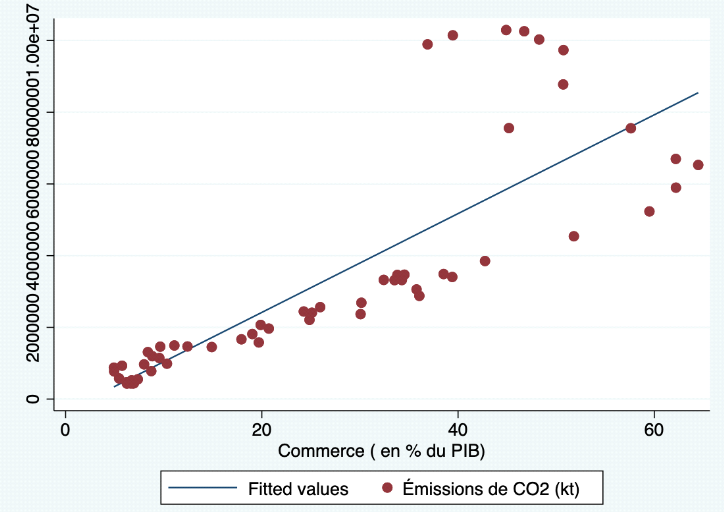
b) Régressionlinéaire:
Afin de pouvoir étudier les conséquences du
commerce et plus particulièrement du commercechinois depuis leur
ouverture au monde sur l'environnement et la pollution dans le pays, nous
allonsétablirunerégression linéaire.
Je cherche à quantifier ici l'évolution de la
variable expliquée CO2 dans le cas ou la
variableexplicativecommerceaugmenterai d'uneunité.
Letableau13enannexereportantlescoefficientsderégressionnousdonnelavaleurdel'ordonnéeàl'originedeladroite,autrementditlaconstanteBeta0quiestégaleà-673778.Or,celasignifierait
que si le commerce était au niveau 0, c'est a dire que s'il n'existait
pas, les émissions deCO2seraientégales à-673 778.
Cettedonnéen'aaucunsenséconomiqueetrestepeuinterprétableenrèglegénérale.
Beta1iciestégalà145521cequirevientàdirequesilecommerceaugmented'uneunité,lesémissionsdeCO2
augmenteraientde145 521 Kt.
La valeur p teste l'hypothèse nulle que le coefficient
est égal à zéro et a aucun effet. Une faiblevaleur p
(<0,05) indique que l'on peut rejeter l'hypothèse nulle. Cela revient
à dire q'une
variableexplicativequiaunefaiblevaleurpestsusceptibled'êtreunajoutsignificatifaumodèleparceque
les changements dans sa valeur sont liés à des
changements dans la variable expliquée. Inversement,une valeur p plus
importante (non significative) suggère que les changements dans la
variableexplicativenesontpas associésàdeschangements
delavariableexpliquée.
Ici la valeur p est égale à 0, ce qui signifie
que je peux rejeter l'hypothèse nulle et affirmer que
lavariableexplicativecommerceabienuneffet significatifsurlapollution.
| 


