|
Préambule
Ce mémoire est consacré à l'étude
du modèle mathématique des assurances maladie afin de calculer
la prime de risque qu'un assuré doit verser à son assureur en vu
d'une prise en charge lors de la réalisation du sinistre. Cette
étude a été effectuée à l'hôpital
Saint Joseph de Kinshasa dans le service de
gynécologie-obstétrique et de la Maternité.
En effet l'assurance maladie appartient à la famille
des assurances des personnes, qui proposent des contrats destinés
à protéger les individus des risques qui portent atteinte
à leur intégrité physique.On scinde habituellement les
assurances des personnes en deux grandes familles : l'assurance vie et
l'assurance de dommages corporels.
L'assurance vie propose des contrats dont les prestations sont
versées suite à une atteinte physique à la personne
assurée. Elle offre également des couvertures contre le
décès mais dans un cadre bien défini dans le régime
de prestation.
Elle regroupe les branches suivantes :
- L'assurance santé : a pour but de rembourser des
frais consécutifs aux maladies, aux accidents, à la
maternité. Le niveau de remboursements de frais de soins et des
médicaments varie de la prise en charge de ticket modérateur
à une partie ou à la totalité des frais laissé
à charge de l'assuré.
- L'assurance des accidents corporels : a pour but de
garantir les accidents corporels par versement des prestations forfaitaires ou
indemnitaires en cas d'accident ayant entrainé une incapacité,
une invalidité ou un décès.
- L'assurance dépendance : à pour objectif
de financer l'aide en cas de perte d'autonomie par versement d'une rente et/ ou
d'un capital.
Les promesses faites aux assurées portent la plus part
des temps sur des longues périodes. L'évaluation précise
du coût lié à ces promesses et une gestion saine sont des
conditions essentielles à la viabilité des contrats et aux
versements des prestations prévues.
Au cours de la vie du contrat d'assurance, l'assuré va
passer par différents états qui conditionnent son engagement par
le paiement de ses primes, mais aussi l'engagement de l'assureur à son
égard par le paiement des prestations. L'objet mathématique les
plus approprié pour modéliser l'évolution de
l'assuré à travers ces différents états est
la classe de processus stochastiques à temps continu et à espace
d'états fini appelée processus ponctuels.
Canevas de travail
Ce travail se compose en quatre parties :
- La première partie
intitulée « Généralités sur les
assurances » donne les grandes notions des assurances autres que
maladie en premier lieu et traite singulièrement des assurances maladie
en second lieu ;
- La deuxième partie intitulée « Etude
du système d'assurance maladie en France », est
consacré à l'étude du système d'assurance maladie
en France qui est l'un de meilleur au monde. C'est pour comprendre la
problématique de l'assurance maladie que nous introduisons ce chapitre
car cet assurance est presque inexistante dans notre pays;
- La troisième partie traite des modèles
stochastique de l'assurance hospitalisation avec possibilité des
retours à des états occupés dans le passé du faite
que les états d'hospitalisations sont(heureusement) les plus souvent non
définitif et il est important de pouvoir évaluer les
probabilités de retrouver une bonne santé à tout âge
afin d' évaluer de manière la plus juste possible les primes
associées à ces contrats.
- Et enfin dans la quatrième partie, nous allons faire
une étude sur le calcul de la prime de risque à partir des
données récoltées aux services gynécologie et
maternité de l'hôpital Saint Joseph. Dans cette section nous
utiliserons les techniques issues des statistiques pour la constitution des
échantillons. Nous utiliserons comme outils pour produire nos
statistiques le logiciel SPSS.
Préface
L'assurance maladie qui fait l'objet de notre étude
appartient à la famille des assurances des personnes qui constituent
sans contexte la partie la plus dynamique du secteur des assurances. Toutes les
statistiques disponibles montrent clairement qu'au cours du dernier quart de
siècle passé les assurances des personnes ont connu des taux de
croissance significativement plus élevés que ceux des assurances
des dommages et de responsabilité.
Les explications de ces succès sont multiples ;
citons notamment le vieillissement de la population, une meilleur connaissance
de la part de ménage des risques de l'existence, la crise
économique et l'acquisition d'un revenu vital non certain et, enfin la
crise de l'état providence qui a miné la confiance autrefois
placée dans les mécanismes d'assurances sociales.
L'assurance maladie à un impact positif sur
l'économie d'un pays car les primes versés par l'assuré
constitueront des réserves qui pourront alimenter l'économie du
pays et cette assurance devrait être encouragée plus que tout
assurance car tout être humain est toujours atteint au cours de sa vie
d'une maladie mais tout être ne possédera pas forcement une
voiture ou un immeuble à assurer.
En République Démocratique du Congo, nous avons
en général les problèmes suivant :
- Les démunis ou les personnes sans revenu constant et
décent n'ont pas facilement accès aux soins médicaux et
meurent parfois d'affection bénigne faute des moyens
financiers ;
- Ceux qui possèdent un revenu, dépensent des
sommes importantes étant donné qu'ils supporteront toutes leur
hospitalisation jusqu'au paiement de service post hospitalier
Face à ce problème et consciente de cette
réalité, l'Etat devrait encourager la population à payer
cette assurance et devrait également libéraliser le secteur afin
de créer une compétition dans les prestations des services aux
assurées. Ceci contribuera à l'amélioration du
système d'offre de soins par les réserves constitués car
ceux-ci peuvent être affectés à cette tâche.
L'assurance maladie propose de contrat dont les prestations
sont versées suite à une atteint à
l'intégrité physique de la personne, constitue notre sujet
d'étude en générale. Mais nous nous intéressons
plus précisément à l'assurance hospitalisation car
celle-ci englobe les services connexes qui donnent une vision plus
générale de la prise en charge d'un malade.
Soucieux d'apporter une contribution à la
résolution des problèmes de la RDC, nous nous sommes
intéressés à l'étude du modèle
mathématique pour la tarification de contrat d'assurance hospitalisation
par l'utilisation des techniques statistiques appropriées.
Pour avoir une idée des différents
problèmes que connaissent l'assurance maladie nous nous sommes
intéressés à l'étude du système d'offre de
soins en France qui est l'un des meilleurs au monde comme l'a certifié
l'OMS en 2008. Et cette étude nous permettra de comprendre la structure
de l'assurance maladie en catégorisant les services des prestations
selon les couches de la population.
Chapitre 1 :
Généralité sur les assurances
1.1.
Historique
Les traces lointaines des opérations d'assurance se
trouvent dans l'antiquité où l'assurance était
pratiquée sous la forme la plus ancienne : celle de l'assurance
mutuelle, qui consistait à la mise en commun avec d'autres personnes
exposées aux mêmes risques, des cotisations demanière
à constituer un fond qui devrait parer aux éventualités
prévues.
Déjà à Rome avant le
15èmesiècle il existait des mutualités des
petits marchands, des caisses de secours. Dès lors l'on comprend que
l'assurance a comme base « la mutualité » qui permet
d'éliminer le hasard et de créer la sécurité.
A la fin du moyen âge apparu l'assurance à prime
fixe sous la forme d'assurance maritime ; l'assuré s'adresse
à un tiers qui, moyennant une prime forfaitaire s'engage à
garantir jusqu'à un maximumconvenu. Ainsi l'assistance mutuelle se vit
remplacer par le principe du but lucratif et l'idée de l'association par
celle de la prime, n'étant elle-même que le prix du risque.
Le développement de commerce de mer dans tous les pays
du bassin méditerranéen provoqua l'éclosion de cette
assurance à prime fixe et l'assurance maritime apparut au
15èmesiècle comme une institution organisée.
L'assurance maritime ne constituait au 15emesiècle qu'une
assurance des choses destinée à garantir la cargaison contre le
risque de mer.
Au 17èmesiècle l'assurance terrestre
fit son apparition en Angleterre sous la forme de l'assurance contre l'incendie
à la suite du grand incendie de Londres en 1666 qui détruisit
plus de 13000 maisons et près de 100 églises.
Au 19èmesiècle, l'assurance prit son
essor par la création de plusieurs compagnies privées, mutuelles
sous action. A coté de l'assurance incendie des nouvelles formes des
assurances virent jour : les assurances contres les accidents, les
assurances de responsabilité.
Au 20èmesiècle, on assiste à
un développement de l'assurance favorisé d'une part par la
concentration des populations dans les villes, d'autre par
l'amélioration du niveau de vie et l'établissement des
statistiques des plus en plus précises et des tables des
mortalités par les mathématiques des assurances.
Le développement du machinisme et la circulation
automobile accrurent les formes d'assurancesde responsabilité
déjà connues et sous l'influence de la vie économique et
sociale, les assurances contre les vols, contre les risques de guerre, les
assurances contre les accidents corporels apparurent.En outre,
l'évolution des assurances au 20èmesiecle se
caractérise par une socialisation qui se manifeste à un triple
point de vue.
D'une part il ya des risques qui menacent l'individu dans sa
personne (maladie, invalidité, vieillesse,...) et dont la couverture
présente un intérêt social évident. Les personnes
menacées par ses risques et qui sont économiquement faibles ne
sont pas capablede s'assurer. Ainsi, tenant compte de l'intérêt
général, l'Etat est intervenu pour s'imposer à tous les
salariés, avec la participation des employeurs, la couverture de ses
risques sociaux afin d'améliorer, par la sécurité le sort
de la classe ouvrière.Dès lors les assurances contre les
maladies, les assurances contre les accidents corporels, les assurances en cas
de vie ou assurances retraites naquirent.
D'autres parts, la socialisation des assurances se manifeste
au sein même des assurances privées, car dans plusieurs pays, les
assurances sont exploitées par les sociétés privées
et, dans d'autres, on a institué le monopole et l'étatisation
des assurances, comme c'est le cas en RDC.
Par ces diverses manifestations, on
aperçoitl'évolution que l'assurance a subie depuis plusieurs
années.
1.2. Définitions
A la base des notions générales d'assurance on
trouve des éléments économiques, juridiques et
techniques.Ainsi à travers les âges, les économistes, les
juristes et les techniciens ont émis diverses théories sur la
notion d'assurance selon leurs disciplines.
Dans l'assurance les économistes ont surtout retenu
l'idée de besoins (besoin d'assurer son pain quotidien, besoins de se
protéger contre les pertes éventuelles,...) pendant que les
juristes ont insisté sur l'idée des dommages et sur les
prestations incombant à l'assureur et à l'assuré.
Les techniciens quand à eux ont mis en évidence
le fait que l'assurance ne peut remplir son but que si elle se manifeste
à l'état isolé, c'est-à-dire limité à
un seul risque dans le rapport d'un seul assuré et d'un assureur. Le
besoin de sécurité total ne peut être satisfait
parfaitement que si on recourt à l'aide d'autrui.
Déjà en 1994 Chaufton l'avait souligné en
déclarant que « l'assurance est lacompensation des
effets du hasard par la mutualité organisée suivant les lois de
la statistique ».D'autres technicien tel que le professeur
VIVANTE ont mis en valeur l'idée que l'assurance est
« un office de réparation dont le rôle est de
distribuer les primesrecueillies dans un groupe des nombreux d'assuré
entre ceux qui ont subi des sinistres ».
Par essence, l'assurance suppose donc une réunion des
personnes qui, pour faire face à un même risque susceptible de
les atteindre, décident de contribuer tous aux règlements des
sinistres éventuels. Le but de l'assurance ne peut donc être
atteint par le regroupement d'une multitude d'assurés au sein d'une
même entreprise, au sein d'une même mutualité qu'est
l'assureur.
Dans une formule simplifié, on peut donc définir
l'assurance comme é étant « une
opération par laquelle une partie, l'assuré, se fait promettre
moyennant une rémunération, la prime ; une prestation par
une autre partie, l'assureur en cas de réalisation d'un
risque ». Cette définition met en valeur les rapports
qui naissent entre l'assureur et l'assuré, et fait naitre les deux
obligations réciproques essentielles, à savoir le paiement de la
prime à la charge de l'assuré et la prestation de l'assureur lors
de la réalisation du risque.
Reprenant les trois caractéristiques examinés ci
avant : économique, juridique et technique -J.HEMARD -a
donné une définition plus complète de l'assurance :
« Opération par laquelle une partie, l'assuré,
se fait promettre, moyennant une rémunération, la prime ou
cotisation pour lui ou pour tiers en cas de réalisation d'un risque, une
prestation par une autre partie l'assureur, qui prenant en charge un ensemble
de risques, les compense conformément aux lois de la
statistique ».
Cette définition s'applique aussi bien aux assurances
des dommages qu'aux assurances des personnes, aux assurances mutuelles qu'aux
assurances à prime fixe et met en valeur les trois
éléments essentiels de l'assurance, à savoir le
risque, la prime et la prestation de
l'assureur.
L'assurance ainsi définit remplit les fonctions
diverses tant du point de vue individuel que du point de vue
socio-économique.
Sur le plan individuel, au regard du caractère moral de
l'assuré, l'assurance est un produit de la vertu de prévoyance.
Avec l'assurance, l'assuré prend ses précautions, il songe
à l'avenir. L'assurance confère à l'assuré ;
la sécurité dont il a besoin en lui apportant confiance dans
l'avenir et en le protégeant contre les risques du hasard qui le
menacent, lui et son patrimoine.
Du point de vue économique l'assurance permet par
l'accumulation des primes, la constitution des capitaux qui présentent
un intérêt à la fois pour les assurés et pour
l'économie nationale.
Sur le plan social l'assurance empêche un grand nombre
de gens de tomber à charge de l'assistance publique en fournissant
indirectement des ressources à l'Etat et aux collectivités
publiques en vue de la satisfaction des besoins essentielles de la nation.
En dehors des fonctions ci-dessus examinées, il
importe de souligner l'importance de l'internationale de l'assurance. En tant
que technique, l'assurance repose essentiellement sur l'existence d'une
mutualité qui est le regroupement d'une multitude de risques. Les
risques étant semblables dans la plus part des pays, l'assurance doit
déborder les frontière nationales ; ce qui fait qu'elle n'a
pas des limites géographique.
Son rôle international se réalise donc par
« réassurance » c'est-à-dire la session par
l'assurance qui, tout en demeurant seul responsable vis-à-vis des
assurés pour les risques qu'il a accepté de couvrir, cède
une partie plus ou moins importantes de ces risques à un
réassureur des sortes que les incidents des sinistres nationaux se
répercutent en définitive sur l'économie de plusieurs
pays ; ce qui constituent un facteur d'équilibre et de
stabilité générale pour la mutualité.
L'opération de réassurance apparait alors comme
une série d'assurance successive diluant le risque à un
degré tel qu'il ne peut plus être la cause d'une charge
élevée pour chacun de participant.On distingue la
réassurance des sommes qui a pour but de réduire le montant du
risque couru par l'assureur direct et la réassurance des dommages
fondée sur l'idée du sinistre ; elle a pour but de
réduire la charge de l'assureur direct du fait des indemnités
versés au bénéficiaires des contrats d'assurance.
1.3. Eléments de l'assurance
Toute assurance repose essentiellement sur trois
éléments : le risque, la prime et la prestation de
l'assureur.Dans les assurances de dommages, on observe un quatrième,
à savoir l'intérêt d'assurance, en effet toute personne
ayant un intérêt à la conservation d'une chose peut la
faire assurer.
1.3.1. Le risque
Dans le langage courant le risque est synonyme de danger mais
en matière d'assurance, le risque constitue un événement
incertain, il implique l'idée de l'éventualité. Ainsi dit
on que l'assurance repose sur l'aléa c'est-à-dire elle porte sur
des faits déterminés qui comporte une incertitude.
Le risque est donc l'élément fondamental de
l'assurance ; c'est pour se couvrir contre le risque que l'assuré
traite avec l'assureur. Cependant tous les risques ne sont pas
assurables ; un risque putatif (celui qui se déjà
réaliser au moment de la signature du contrat) n'est pas admis en
matière d'assurance ; il s'agit d'une assurance arrière
selon le vocabulaire allemand. De même les risques purement potestatifs
(dont la réalisation dépend uniquement de la volonté de
l'assuré) ne sont pas acceptables. Dans ce cas l'aléa est
supprimé car le risque n'existe plus. Il ne peut pas avoir d'assurance
pour le sinistres causés intentionnellement car le hasard n'intervient
plus c'est-à-dire l'événement échappe à
l'incertitude.
Le risque assurable doit être un évènement
futur ; et l'évènement en question peut être
malheureux (dommage causé par l'incendie,...) ou heureux (cas de
l'assurance vie en cas de survie, hospitalisation due à un accouchement,
l'assurance dotale faite en vue de doter les enfants,...). La
réalisation du risque ou la survenance d'un évènement
(heureux ou malheureux) est appelé
« sinistre ».
Les risques assurables ne présentent pas tous le
même caractère ; selon les cas ils sont constants ou
variables, suivant les conditions de probabilité de leur
réalisation. Le risque constant est celui dont les chances de
réalisation restent les mêmes pendant la durée de
l'assurance tandis que le risque variable est celui dont les chances de
réalisation augmentent (risque progressif) ou diminue (risque
dégressif) au cours de l'assurance.
Hormis son sens d'évènement incertain et
indépendant de la volonté des parties, le mot risque indique
aussi « la valeur du risque » à assurer
c'est-à-dire le degré de probabilité de la survenance de
l'événement envisagé (les chances que ce risque à
se réaliser). En matière d'assurance de dommages, le risque
exprime la valeur actuelle du dommage possible dans une unité de temps
déterminé.
La valeur du risque est à la base de la théorie
de la prime.
1.3.2. La prime
La prestationpécuniaire du risque pris en charge par
l'assureur est appelée « prime » ou
« cotisation »selon qu'il s'agit d'une entreprise
d'assurance ou d'une mutuelle.
La prime est donc le prix du risque ou de l'assurance.
Les éléments qui entre en compte pour la
fixation de la prime ou des tarifs commerciale sont de deux sortes :
D'une part il ya la prime pure ou théorique dont la
détermination est d'ordre technique et résulte des données
statistiques qui permettent de déterminer les chances de
réalisation de risque. En s'appuyant sur les faits passés, les
statistiques permettent de dégager, pour l'avenir des lois de
survenances c'est-à-dire la probabilité de survenance des
sinistres.
Ainsi le calcul de probabilité donne à
l'assurance une base scientifique sûre. La prime pure dépend dont
essentiellement du risque à courir, elle est fonction de celui-ci.Sa
déterminationdépend de la probabilité de survenance de
sinistre qui se mesure par le rapport entre les chances favorables et les
chances possibles de réalisations du risque. Le taux de la prime pure
est aussi influencé par l'intensité de sinistre
c'est-à-dire par l'importance de ses conséquence.
D'autre part il y ades chargements qui comprennent les frais
d'acquisition des contrats, les frais fixes, les frais de gestion ou
d'administration et les taxes ou impôts. Dans le langage des assurances,
ces éléments constituent « le chargement ».La
prime pure augmentée du chargement devient ainsi la prime chargée
ou commercial que l'assuré doit effectivement acquitter.
1.3.3. La prestation de l'assureur
La prestation de l'assureur intervient lors de la
réalisation du risque c'est-à-dire à la survenance du
sinistre. C'est cette contrepartie de l'obligation de l'assuré,
à savoir la prime que consiste essentiellement au décaissement
d'une somme d'argent de l'assureur pour couvrir le besoin contre lequel
l'assuré a voulu se garantir.
En assurance de dommage ou de choses, cette prestation est
appelé« indemnité » tandis
qu'en assurance de personnes ou des capitaux elle est appelée
« bénéfice ». En assurance de dommages la
mesure de la prestation de l'assureur est fonction de la valeur du risque et du
dommage subi par l'assuré lors du sinistre ; tandis que dans les
assurances des personnes, c'est la somme assurée qui seul
détermine la mesure de l'obligation de l'assureur.
L'assureur promet toujours un capital en fonction de la prime
qu'il reçoit. Ici, c'est donc le contrat seul qui détermine
l'étendue de la prestation de l'assureur, les sommes assurées
étant librement et définitivement fixées par la police.
Parfois, pour faire obstacle à toute fraude ou estimation
exagérée du dommage dans certain assurance de dommage,
l'assureur se réserve la faculté de
réparer en nature au lieu de verser une somme d'argent.
1.3.4. Le contrat d'assurance
Le contrat d'assurance intervient entre l'assureur et le
souscripteur. Ces deux personnes qui signent les contrats constituent
« les parties contractantes ».
L'assuré souscripteur est celui dont les biens ou la personne sont
exposés au risque. Le contrat d'assurance s'établit pratiquement
par un document écrit appelé la
« police » ou à défaut,
surtout de façon provisoire une « note de
couverture ». La police est donc l'acte qui constate le
contrat d'assurance.
En principe le contrat d'assurance produit un effet
immédiat c'est-à-dire sa prise d'effet coïncide avec
sa conclusion ; ce qui fait que tous sinistre postérieur à
ce moment est automatiquement garantie. La police d'assurance comprend les
parties suivantes :
1) Une proposition d'assurance : qui renseigne sur la
nature et l'objet du risque à assurer (chose oupersonne) et sur les
identités des parties contractantes (nom, adresse et profession de
l'assuré, raison social de l'assureur). Une protection d'assurance doit
obligatoirement être signée par l'assureur et l'assuré.
Un exemplaire des conditions générales :
c'est l'ensemble des règles applicables à tout le monde pour une
branche d'assurance donnée. Les conditions générales
définissent en grandes lignes :
L'objet de l'assurance, les risques garantis, les risques
exclus, les modalités de paiement de la prime et ce qu'il faut faire en
cas de sinistre.
2) Un exemplaire des conditions particulières :
c'est-à-dire l'ensemble des règles relatives à un
assuré particulier. Souvent elles complètent ou dérogent
les conditions générales aux moyens des clauses
particulières. Outre l'identité complète de
l'assuré, elles définissent la durée de l'assurance
appelée « échéance »,
les limites de la garantie, le décompte de la prime, les clauses
particulières s'il ya. S'il s'agit d'une police d'assurance sur la vie
et sur la santé, il faut indiquer la date de naissance de celui sur la
tête de qui repose l'opération.
3) Le reçu : qui acte le paiement de la prime.
4) Un ou plusieurs avenants : qui indiquent les diverses
modifications intervenues au cours de la gestion de la police.
Hormis le reçu, tous les documents doivent être
conjointement signés par l'assureur et l'assuré.
1.4. Classification des assurances
Les assurances sont classifiées d'après la forme
des entreprises d'assurance et d'après leur objet.
1.4.1. D'après la forme
D'après la forme, on divise les organismes d'assurance
en « mutuelles » et en
« compagnies à primes fixes ».
1.4.1.1. Les
mutuelles
Elles constituent les assurances fondées sur la
solidarité des assurés sans que l'organisme assureur cherche
à réaliser des bénéfices. Elles ont une nature
essentiellement civile parce qu'elles ne sont pas fondées sur
l'intention de lucre. Du point de vue de leur fonctionnement, les
mutualités sont simplement immunisées contre un danger commun en
dehors de toutes idées de spéculation et sont en même
temps leur propre assureur ; les mutualités par l'organe de la
mutuelle ; répondent en définitive de perte
éventuelles résultant des risques couverts et la cotisation leur
réclamée varie suivant la gravité du risque à
couvrir.
Néanmoins, ladite cotisation est limitée, dans
la pratique, à un maximum déterminé, c'est ce qui entraine
la relativité de la responsabilité dans la mutuelle. S'il ya
insuffisance des sommes exigibles, versées ou à verser par les
mutualités, il ne sera accordée qu'une identité
partielle, en cas de sinistre. Il importe de signaler que le mutuelles ne
recourent pas aux services des courtiers et agents d'assurance ; elles
payent donc rarement les commissions d'usage.
1.4.1.2. Les
assurances à prime fixe
Ces assurances sont fondées sur le but de lucre ;
elles sont toujours pratiquées par des sociétés
commerciales (société par action, plus exactement anonyme). Sur
le plan fonctionnel, les assurés n'ont aucun point de contact entre eux
comme dans les mutuelles ; il n'existe que de lien des droits entre chaque
assuré et son assureur. Dans l'assurance à prime fixes, il ya
invariabilité de la prestation des assurés et la
responsabilité de l'assureur est toujours entière.
Des nos jours ces deux formes d'assurance ont réagit
l'une sur l'autre et se sont interpénétrées ; ce qui
a diminué de plus en plus l'opposition entre les deux.Certaines
sociétés d'assurance mutuelles acceptent déjà des
contrats d'assurance à primes fixes.Aussi, dans certaine branche de
l'assurance à prime fixes, surtout dans l'assurance-vie, les
assurés participent dans une certaine mesure, aux
bénéfices de la société.
Toujours d'après la forme de l'organisme d'assurances,
on distingue également les assurances publiques des assurances
privées et des assurances sociales.
L'assurance publique est exploitée par le pouvoir
public ou par un établissement public (dans ce cas l'état joue
le rôle de l'assureur). Tandis que les assurances privées
poursuivent un but de réparation d'un préjudice causé
à l'assuré.
Ces assurances n'existe dont qu'à l'échelon
individuel dans ce sens qu'elles ne tendent qu'à assurer la
sécurité individuelle des assurés et non une
sécurité collective. Elles sont obligatoires, c'est le cas des
accidents des travaux, assurance de responsabilité civile
automobile...
Par contre les assurances sociales intéressent des
groupes sociaux entiers sans tenir compte des individus ; elles sont
libres ou partiellement libres. Par exemple, les assurances maladie, assurances
invalidité, assurance vieillesse et décès
prématuré, allocation familiale, assurance chômage (ici il
ya assurance et assistance mélangées),...
Les assurances sociales se caractérisent par l'absence
de but de lucre des organismes assureurs, l'absence des sélections de
risques d'où l'importance de la prévention et par leur
caractère de service public, d'où le contrôle de l'Etat.
Aussi faut-il souligner le recours à d'autres (contribuables) pour
compléter les cotisations des assurés.
1.4.2. Suivant leur objet
Suivant leur objet veut dire suivant les risques qu'elles
courent, on distingue les assurances des dommages ou de chose et les assurances
des personnes ou des capitaux suivant qu'elles portent sur une chose ou une
personne.
1.4.2.1. Les assurances des dommages
Elles sont également appelées assurances
d'intérêt ou assurance-indemnités. Elles garantissent
l'assuré contre les conséquences d'un évènement
pouvant causer un dommage à son patrimoine. Elles sont indemnitaires
c'est-à-dire elles réparent les préjudices patrimoniaux
produits par un sinistre.
Les assurances de dommages se subdivisent en assurances des
choses et en assurances de responsabilité
a) les assurances des choses : elles ont pour but
d'indemnisé l'assuré de pertes matérielles qu'il subit
directement dans son patrimoine lors de la survenance du sinistre.
Exemple : l'assurance contre l'incendie, l'assurance contre le vol,
l'assurance contre la grêle, contre la mortalité de
bétails.
Les sinistres en cas d'assurance des choses met en
présence deux personnes, l'assuré et l'assureur
b) les assurances des responsabilités garantissent
l'assuré contre les préjudices qu'il cause aux tiers et qui
engagent sa responsabilité. On les qualifie d'assurance des dettes. Le
sinistre en cas d'assurance de responsabilité met en présence
trois personnes : les tiers lésé ou la victime,
l'assuré et l'assureur.
Ex. Assurance responsabilité civile incendie (risque
locatif ou recours des voisins), assurance R.C automobile, assurance R.C
professionnelle, assurance R.C travaux...
Les assurances transports couvrant les risquent
inhérent aux transports maritimes, fluviaux, terrestres et
aériens appartiennent aussi à la catégorie des assurances
de dommages. Les contrats y relatifs sont indemnitaires.
1.4.2.2. L'assurance des personnes ou des capitaux
Cette assurance englobe toutes les assurances qui visent
l'assuré dans sa personne, quant à son existence, à sa
santé ou à l'intégrité de son corps. C'est donc la
personne même de l'assuré qui est prise en
considération.Les assurances des personnes, à la
différence des assurances de dommage, ne présentent pas un
caractère indemnitaire ; elles n'ont pas pour but de réparer
les préjudices.
Lors de l'arrivé des l'évènement
envisagé, l'assureur exécute intégralement et sans
réserve les prestations promises au moment de la conclusion du
contrat.
En assurance des personnes ou des capitaux, on distingue les
assurances contre les accidents et les assurances sur la vie
a. Les assurances contre les accidents
Les assurances de personne du domaine des assureurs accidents
comprennent les assurances contre les conséquences d'accidents corporels
et les assurances garantissant les conséquences des maladies. Ces
assurances prévoient deux natures de garanties :
- Le versement d'indemnité en cas d'interruption de
l'activité de l'assuré due à une circonstance
prévue par le contrat.
- Le remboursement des frais entrainés par un accident
ou par une maladie, suivant l'objet du contrat.
Techniquement les assureurs accidents considèrent que
leurs assurances de personnes constituent des assurances de réparation
au contraire des assurances vie dont les techniques reposent sur la tables de
mortalité qui permet de calculer les probabilités viagères
c'est-à-dire la probabilité de vie ou de décès.
A la société nationale d'assurance, l'assurance
contre les maladies n'est pas encore exploitée, jusqu'à ce jour,
seules les assurances contre les accidents corporels sont pratiquées par
la « direction des accidents et risques divers ».
Ces assurances garantissent aux assurés à titre
principal, des sommes déterminées en cas d'accidents corporels
entrainant des conséquences prévues par les contrats et à
titre accessoire les remboursements des frais médicaux, pharmaceutiques,
chirurgicaux... qu'ils ont engagés à la suite des accidents.
b. L'assurance individuelle ou individuel
accident
Elle garantit le paiement d'indemnité à la
personne assurée ou aux bénéficiaires
désignés s'il lui arrive un accident corporel, soit dans
l'exercice de sa profession, soit au cours de sa vie privée.
c. Collective accidents
Si l'assurance contre les accidents corporels, au lieu de
couvrir le risque d'accident pour un seul individu, garantit un ensemble
d'individus, elle porte alors le nom d'assurance collective ou cumulative.
Cette assurance est généralement souscrite par les entreprises au
profit de tout ou partie de leur personnel.
d. Assurance accident de travail
Elle couvre l'assuré contre l'accident pouvant survenir
sur le lieu de travail ou encore sur le trajet aller retour du domicile au lieu
de travail.
e. Assurance accident occupant auto
Cette assurance a pour but de garantir le paiement des
indemnités convenu à l'assuré à la suite d'un
accident corporel dont il pourrait être victime soit quand il est
transporté dans un véhicule, soit quand il y monte ou quand il y
descend.
f. Assurance accident voyage
Cette assurance a pour but de garantir à
l'assuré le paiement des indemnités convenues au cas ou
il pourrait être victime d'accidents corporels au cours du voyage
par tous le moyen régulier de transport public ou privé ainsi
qu'au cours des séjours consécutifs à ces voyages.
Les assurances ci-dessus énumérées
garantissent le mêmes risques à savoir le décès,
l'invalidé ou l'infirmité permanente totale, l'incapacité
temporaire et les frais médicaux et produits pharmaceutiques.
Les polices pour éviter dans la mesure du possible les
difficultés, comportent généralement une liste importante
d'exclusions. Certains risque sont exclus d'une manière
générale et ne peuvent faire l'objet de couverture par clause
particulière ; d'autres, au contraire, peuvent être couverts
moyennant stipulations aux conditions particulière et sur primes.
Chapitre2 : Etude du
système d'assurance maladie (cas de la France)
Introduction
Dans cette partie nous parlerons de l'assurance maladie en
regard de l'organisation, administrative et du système d'offre de soins
en France, dans le but d'appréhender de façon claire la
problématique de la dépense, du financement et de l'organisation
selon les couches sociaux.
Contrairement aux autres sortes d'assurances des personnes,
l'assurance maladie n'est pas que le produits des ordonnances mais de mouvement
de la population selon les classes qui ont senti la nécessité des
cogestions des dispositifs médicaux entre partenaires sociaux afin de
partager le frais dû à ce soins qui ne sont pas toujours à
leur porté.
Mais néanmoins l'assurance maladie ne doit pas
être confondue avec la sécurité sociale au sens large dont
elle n'est qu'un des aspects, comme son nom l'indique.Entre
protégé et soigné contre une affection de longue
durée, comme le cancer ou l'hypertension, peut sans doute relever de la
logique sociale. Reste que de telles maladie frappent quelques soient les
proportions, parmi toutes les couches de la population ; elles appellent
donc une couverture pour tous et une « gestion du risque »
au sens assurantiel du terme.
Cette gestion du risque va servir à calculer les
cotisations que chaque assuré devra payer d'une manière aussi
précise que possible afin d'éviter les prélèvements
inutiles sur la richesse des entreprises pour les travailleurs et sur les
revenus des citoyens afin de ne pas accroitre ce que les économistes
appellent « les effets
d'éviction ».
2.1. L'assurance maladie produit d'une lente
évolution
Comme vous allez le remarquer dans les lignes qui suivent,
l'assurance maladie à mis beaucoup de temps pour se constituer en
système vraiment organisé.Deux processus qui constituent les
prémisses de l'assurance maladie vont aller en parallèle.
D'un coté un souci d'auto organisation avec le principe
mutualiste appuyé sur les sociétés de secours et
d'entraide, et de l'autre coté un souci de l'état de
prévenir les désordres sociaux et donc de confier à des
collectivités publiques étroitement contrôlées par
lui le soin de remédier aux situations les plus pénibles.
Il importe de souligner qu'à la base, l'assurance
maladie aura été conçue comme intrinsèquement
relié au monde du travail. C'est celui qui travail qui est aussi
assuré contre les risques d'une maladie. Le travailleur est
assuré non seulement pour les soins qu'il peut recevoir, mais aussi pour
obtenir un revenu de remplacement au travail qu'il peut accomplir si la maladie
le frappe. On remarque que l'assurance maladie oscille entre la protection
sociale qui s'adresse au travailleur d'une part, et les notions assurantielles
relié au monde de l'emploi d'autre part.
Il s'agit alors d'un mélange subtil entre
solidarité social consentie entre membres d'un groupe et aussi risque
d'assurance pour la maladie ou pour une pension pour les vieux travailleurs. A
ce temps là, l'entraide était toujours temporaire et n'offrait
pas de service à long terme. Ce qui explique facilement la faiblesse des
cotisations.
Ces sociétés de secours mutuelles dont
l'objectif est de venir en aide aux travailleurs malades, aux enfants et aux
veuves illustrent parfaitement le besoin humain de prévoyance et de
sécurité.Il en est un fait que ces sociétés
mutualistes sont bien la matrice qui va produire plus tard la
généralisation de la sécurité sociale plus
précisément dans sa composante d'assurance maladie.
Les dirigeants de la troisième république
française comprennent l'intérêt d'un dispositif d'aide aux
malades qui ne peuvent subvenir au coût des soins ainsi que la grande
détresse et la misère de certaines couches de la population
abandonnées à elles mêmes, d'où ils ont eu le choix
de confier ces charges à des collectivité publiques sur
lesquelles l'Etat pourra exercer son étroit contrôle.
C'est ainsi que l'on confie au département via la loi
du 10 Aout 1893 les soins d'organiser un dispositif médical pour le
plus démunis ; avec ce texte, on glisse de la notion d'assurance
sociale à celle de la protection social, avec la mise en place d'un
filet protecteur pour les plus démunis sans aucun lien précis
avec le travail.
Sur la pression de secours mutuel, le parlement vote une loi
le 1 avril 1898 autorisant les sociétés à fonder de
dispositifs permanent en tous domaines de prise en charge social (retraite,
assurance vie, assurance décès et accident).
Quelques jours plus tard la loi du 9 avril 1893 sur les
accidents de travail instaure un principe d'assurance obligatoire. Ce mouvement
se complète d'une loi du 5 avril 1910 qui institue un régime
d'assurance vieillesse lui aussi obligatoire.Pour les lois du 5 avril 1928 et
du 30 avril 1930, le parlement aboutit à un dispositif global
d'assurance obligatoire. Ce système couvre les risques
décès, invalidité, maternité, maladie et
vieillesse.
Reste que ce dispositif est limité par un
système de plafond de cotisation : on ne cotise de façon
obligatoire que pour un plafond de revenu. En 1930, on crée une loi qui
corrigent pour partie celle de 1928, crée des exceptions qui limitent le
caractère universel en divisant les populations couvertes (agriculteurs,
mécanicien, enseignant, tailleurs,...).Ce qui importe de remarquer
à ce stade, c'est que la notion d'assurance maladie n'est pas les
moteurs des progrès sociaux d'avant guerre. Le système
hospitalier est largement dans les mains de logiques caritatives ou des
religieux prennent souvent une part prédominante. La médecine de
pointe est souvent hors des murs des hôpitaux et les médecins de
ces structures ont la possibilité de percevoir directement leurs
honoraires sous une forme libérale alors qu'ils sont dans cette
situation des soins pour des assurés solvabilisé à 10% par
l'argent quasi public.
Bref l'assurance maladie se constitue par couches et strates
en empilage, sans rarement faire le ménage avec les structures
existantes redondantes. Les besoins de l'universalité est certes
ressenti, mais prédomine le souci de préserver des logiques
d'adhésions volontaires plus proches des choix corporatives.
2.2. Reforme de 1945 et ses prolongements
En 1945 a été mise au point un processus de
généralisation traçant une voie qui se définit
dans 2 textes principaux.
1) En octobre 1945, on crée un réseau
coordonné de caisses locales centrées sur plusieurs organismes.
Parmi ces organismes nous avons le salariat qui dépasse à peine
30% de la population, les petits commerçants, les artisans ruraux, les
agriculteurs auxquels s'ajoutent les professions libérales. Tout
étant des métiers qui entrainent une forte suspicion contre le
salariat et n'entendent pas être mélangés avec lui. ce
réseau coordonné constitue « le régime
général ».
2) Il y aussi des « régimes
spéciaux » constitué de fonctionnaire, des marins, des
mineurs et des cheminots qui vont refuser de joindre le régime
général. Ils veulent tous gérer dans leur autonomie propre
et avec leur propre niveau de prestation. Ils conservent donc un cadre dit
« provisoire »
3) En mai 1946, on notera toute fois à ce stade le
refus de généralisation des assurances sociales par le
travailleur non agricoles et non salariés, appelés les
« non-non ».
En partant de là, on doit constater un refus
d'assurance maladie unique de ces professions qui veulent dans toute la mesure
du possible s'organiser par métiers.S'agissant plus
généralement de généralisation, celle-ci va
s'accomplir de façon progressive par des fusions/absorptions des petites
caisses souvent organisées par métiers et possédant des
régimes de prestations spécifiques. Ceci a été
occasionné par les évolutions démographiques et des
transformations économiques qui sont défavorable à ces
petites caisses.
La généralisation possède cependant des
avantages et des inconvénients, les fusions ont pour avantages de
« solvabiliser » collectivement les régimes en
question tout en échangeant cela par une perte de pouvoir autonome et
une harmonisation des régimes de prestations.
Cependant, ce mouvement génère une
répartition nouvelle des charges qui n'est pas forcement très
équitable, car le salarié du régime général
peut ressentir l'impression de servir de bouée de secours à des
systèmes en perdition.
C'est pourquoi en 1945, une loi va étendre l'assurance
maladie général obligatoire au salariat, lesquels appuyés
sur des puissantes mutuelles, ne veulent pas de rattachement au régimes
général et pas d'harmonisation de leur régime de
prestation. Tandis que les fonctionnaires de régimes spéciaux
sont farouchement attachés en général à leurs
systèmes de prestations qui possèdent des
spécificités plus centrés sur les questions de retraite ou
des prestations familiales complémentaire à l'assurance maladie
qui est presque identique pour les différents régimes.
Ensuite en 1961, le régime d'assurance maladie
obligatoire sera imposé aux exploitants agricoles, qui initialement
pouvaient cotiser sur une base volontaire mais pas obligatoire.
Enfin la généralisation dans le sens de
l'universalité de l'assurance maladie est en principe accomplie par la
loi de 28 juillet 1999 sur la « couverture médicale
universelle »(CMU).
2.3. Généralisation effective de l'assurance
maladie
La CMU est tout d'abord un transfert au plan de principe de la
protection sociale classique vers l'assurance maladie proprement dite. On
dépasse donc la loi de la protection sociale qui supposer que les
personnes avaient les moyens de s'assurer effectivement (salariat,
commerçant,...) car on vise évidemment la population la plus
démunie qui ne dispose pas des moyens.
Ce nouveau dispositif CMU prévoit non seulement
d'affiler obligatoirement les populations concernées à un
régime de base d'assurance maladie, mais il prévoit aussi et
c'est là sa novation, d'accorder le bénéfice d'une
protection complémentaire afin que soit pris en charge celle de
prestations que le régime de base ne prend pas en compte.
C'est notamment les cas du forfait hospitalier (sorte de taxe
hôtelière non relié aux soins de l'hôpital et qui
s'applique aux malades hospitalisés lors de leurs soins).Pour être
ayant droit de ce dispositif les personnes sont bien évidemment soumises
à un plafond de ressources. Pour compléter le dispositif en ce
qui concerne la protection sociale complémentaire au delà des
prestations de régime de base, on notera qu'en 2004, on a
instauré un crédit d'impôt destiné à aider
les personnes qui dépassent le seuil d'admission à la CMU de
moins de 15% à prendre une assurance à complémentaire,
afin de limiter ce qu'on appelle les « effets de
seuils ».
Avec ce système la notion de protection sociale n'a
donc pas disparu avec la CMU et le principe « assurantiel »
est renforcé.
2.4. Structure de l'assurance maladie en France
L'assurance maladie est subdivisée en 3 grands
régimes :
- Le régime général qui possède
une trésorerie qui s'appelle « caisse nationale d'assurance
des travailleurs salariés »
- Le régime agricole ou la mutualité sociale
agricole ;
- Les régimes des indépendants (RSI) regroupant
les commerçants, les artisans et les professions libérales.
Chacune de ces structures dispose d'instances locales
réparties selon leurs spécificités propres sur le
territoire ; ces caisses se finance principalement par les cotisations et
l'impôt. Dès lors, nous observons que tout citoyen français
est affilé obligatoirement à un régime de
sécurité social. S'il est malade, il touchera un revenu de
remplacement partiel ou total ; obtiendra un remboursement partiel ou
total des frais qu'il expose au titre des soins médicaux ;
remboursement qui pourra être complet s'il est en affection de longue
durée ou mutualiste, si son assurance privée couvre ce risque
complémentaire ou s'il est couvert par la CMU.
C'est ce dispositif dense et très complet qui est
considéré par l'OMS depuis l'année 2000 comme l'une des
meilleurs systèmes de santé au monde.
2.5. Problématique de la
dépense de l'assurance maladie
Beaucoup des gens surtout dans le pays développer comme
la France, l'Allemagne, semblent résignés et estimeraient presque
qu'ils n'ont jamais connu d'assurance maladie en déficit. Pourtant
l'assurance maladie a toujours rimé avec déficit, même
minime qu'il soit dans certains pays.
Les montants des recettes générées par
les assurances maladie sont si importants que le déficit ne signifie pas
grand-chose pour la population.Ces dépenses sont condamnées
à progresser pour 3 raisons essentielles sur lesquelles il n'est pas
possible d'influer drastiquement.
- Tout d'abord la population vieillissante est si importante,
malgré une forte natalité, c'est qui conduit à la prise en
charge des personnes âgées qui peut coûter chère s'il
elle est indiqué dans le régime de prestation. Ceci est surtout
valable pour le pays en développement.
- Le durcissement des normes de fonctionnement des
établissements sanitaire et mêmes des cabinets de médecins
libéraux, notamment le spécialiste.
- Enfin, les évolutions technologiques sont par nature
onéreuses, et le principe d'égalité d'accès aux
soins nécessite de les généraliser à tous les
malades.
Il convient ici d'ajouter que l'universalité
d'accès au système de santé à augmenté le
nombre de bénéficiaire du système de santé, et donc
les dépenses. C'est donc la conjoncture économique qui
détermine le rythme des recettes. Cependant dans le cas de notre pays
la RD Congo, la première raison n'est pas valable car l'espérance
de vie de la population congolaise est faible du faite que les personnes ne
vivent pas assez longtemps, et de plus le taux de natalité est
élevé.
La deuxième raison contribuera à
l'amélioration des normes de fonctionnement car l'assuré exigera
de l'Etat ou de l'assureur des normes de sécurité sanitaire plus
strictes.
La troisième raison n'est pas à prendre en
compte car la recherche scientifique dans le domaine de la médecine est
presque inexistante.
2.6. Financement de l'assurance maladie
Le fondateur de la sécurité sociale
française a imaginé un système de financement par des
cotisations sociales, en évitant de faire appel au budget de
l'état.S'agissant de l'aspect recettes, Pierre Laroque a
évoqué 2 raisons pour ce choix de la logique assurantielle du
type Bismarck en Allemagne et, non de solidarité national du type
Beveridge au Royaume Uni :
- Il ne fallait pas subordonner le niveau de prestations de
l'assurance maladie aux logiques financière du budget de l'Etat :
risque de paupérisation.
- L'assurance maladie devrait être alimentée par
ses bénéficiaires, donc fondée sur une logique de
cotisation basée sur les salaires. Il s'agissait bien d'une assurance de
revenu professionnel, ainsi la création ou le maintien de plusieurs
régimes assis sur l'appartenance à un métier a
renforcé cette logique professionnelle.
Aujourd'hui 90% à peu près des prestations
versées par l'assurance maladie n'ont plus aucun caractère
professionnel grâce au caractère obligatoire actuel de cet
assurance, d'où « la fiscalisation du financement de
l'assurance ».
Il faudra alors trouver un bon équilibre entre la
croissance de la richesse national (PIB : produit intérieur brut),
notamment la masse salariale et celle des dépenses de santé
remboursées.
Par ce qui précède nous voyons que l'assurance
maladie n'est pas une véritable assurance car
- les cotisations sont calculées en fonction des
revenus alors que les prestations sont remboursées en fonctions des
besoins, alors que les organismes complémentaires de santé sont
clairement positionnés dans la logique assurantielle de provision de
risque.
- Les recettes et les dépenses de santé
n'évoluent pas selon les mêmes facteurs, d'une part la richesse
nationale (salaire et patrimoine) pour les recettes, d'autre part le
vieillissement de la population et l'amélioration de norme de
fonctionnement des établissements sanitaires.
2.6.1. Source de
financement de l'assurance maladie
L'Etat a créé la contribution sociale
généralisée (CSG) en 1998 et la contribution au
remboursement de la dette social (CRDS) qui s'apparente tous à des
impôts. Progressivement, des taxes ont été rajoutées
aux recettes des cotisations, et l'assuré doit aussi financer le
système par les « reste-à-charge ».
a. Les cotisations et CSG
Les cotisations et impôts de sécurité
sociale sont calculés selon 2 variables : l'assiette et les taux,
qui peuvent être différents s'il s'agit de cotisations patronales
ou salariales.
Ces cotisations sociales (CSG et CRDS) sont
prélevées à la source sur les salaires, ainsi que sur
d'autres revenus tels que les revenus d'activités (contribution
patronale de retraite), le revenu de remplacement, de patrimoine et de
placement ; ceci permet d'améliorer le taux de recouvrement.
L'élargissement de l'assiette était
nécessaire du fait de l'augmentation du chômage et du champ de
prestation ; il fallait ainsi trouver un moyen de rapprocher
l'évolution de recettes et celle du PIB car le salaire seul
n'étant pas pertinent.
b. Les taxes
L'Etat a mis en place des taxes spéciales pour
l'assurance maladie, sont mis à contribution les laboratoires
pharmaceutiques, le conduite à risque, la consommation du tabac et de
l'alcool et même des primes d'assurances automobiles.
c. Les restes à charges
Dans cette rubrique, on trouve un dispositif particulier de
recettes pour l'assurance maladie : le recours contre tiers. Il s'agit
pour l'assurance de récupérer, les sommes payées par les
caisses pour les soins : remboursement au fumeur qui a
développé « volontairement un cancer de
poumon », remboursement du malade qui a détruit
volontairement sa peau ou ses yeux, automobiliste qui a adopter volontairement
une conduite dangereuse.
2.6.2. Impacte de
l'assurance maladie sur le chômage et la régulation
économique
La sécurité sociale dont l'assurance maladie est
composante, a été dévoyée du fait de
prélèvement social dans le PIB. En France par exemple, le
prélèvement de la sécurité social sur le PIB est de
22% donc plus de 60% est affecté à l'assurance maladie.
Les sommes en jeux entrainent de ce fait la
nécessité pour l'Etat d'étudier les effets de ce
prélèvement sur l'économie et l'emploi.
Certains économiste juge que la sécurité
sociale est bonne pour l'économie, car elle permet de relancer
l'économie, étant créatrice d'emploi. Par ailleurs, elle
améliore la productivité du travailleur et contribue à
attirer une main d'oeuvre étrangère qualifiée.
Les charges sur les bas salaires ont connu une très
forte diminution depuis 1993. Le taux de charge est de 2,1% pour le SMIG
(Salaire minimum interprofessionnel garantie) mais de 28,1% pour ces des
employés gagnant plus de 1.6 fois le SMIG. Cette politique a rendu les
cotisations patronales fortement progressives.
Donc comme nous le constatons, ceux qui gagnent plus paie pour
le plus démunie, afin de couvrir les dépenses
supplémentaires.
Chapitre3 : Etude du
modèle d'assurance maladie par l'approche
stochastique
3.1.
Généralités
Dans cette partie, le terme d'assurance hospitalisation fera
référence à l'assurance maladie car l'hospitalisation ne
concerne pas seulement l'internement mais tous le frais post hospitalisation
(fiche, consultation, labo), les frais pré-hospitalisation (achat
médicament, suivie de soins) ainsi que certains services
énoncés clairement dans la police de manière claire et
distincte.
Au cours de la vie d'un être humain celui-ci ne peut pas
échapper à l'attaque de son intégrité physique
suite à une maladie ou un accident. La situation la plus difficile
à prendre à charge est surtout l'internement car, c'est à
ce niveau que beaucoup d'individu peuvent perdre leur vie ou demeurer dans
un état d'invalidité fautes des moyens et de prise en charge non
approprié.
La maladie peut également induire une perte importante
du patrimoine de la personne malade en cas d'affection de longue durée,
même pour les personnes possédant un niveau de revenu
considérable.
Les frais se référant à la prise en
charge de l'individu qui a subit le sinistre sont généralement
élevés ; outre les frais de paiement des médicaments
choisir un hôpital approprié, un médecin
spécialiste, opter pour une chambre individuelle peut augmenter la note
finale de manière importante.
En effet l'assurance hospitalisation ne concerne pas seulement
l'achat des médicaments et l'internement de l'assuré mais
contient plusieurs services énoncés dans la police de
manière claire et distincte.
Prenons l'exemple d'une police d'assurance proposée en
Belgique et en France, en cas d'hospitalisation l'assurance s'engage de prendre
en charge les services suivants :
- Les frais de séjour dans une institution
hospitalière ;
- Les frais de prestations médicales et
chirurgicales ;
- Le frais pré et post-hospitaliers et les frais
engendrés par une maladie grave ;
- Les frais de prestations paramédicales :
infirmière, kinésithérapie,
- Les frais des médicaments et adjuvants
médicaux,
- Les frais de membres artificiel et prothèses
médicales,
- Les frais de transport par ambulance,
- Les frais de séjour et de logement d'un parent pour un
enfant hospitalisé.
En France par exemple les indemnités sont
versées dès le premier jour d'hospitalisation, en cas
d'accident ; et ils sont versés qu'à partir du
huitième jour d'hospitalisation en cas de maladie.
3.2. Caractéristiques supplémentaires des
produits d'hospitalisations
- Tout d'abord, les assurées ont souvent la
possibilité d'opter pour différents niveaux de franchise
annuelle,
- L'accouchement n'est plus souvent couvert que pour autant qu'il
survienne plus de 9 mois après la souscription de la police, pour des
raisons évidentes d'anti sélection.
- Le montant de la prime dépend de l'âge et du sexe
de l'assuré. Les femmes paient une prime plus élevée
par rapport aux hommes principalement à cause des grossesses. La prime
est souvent constante durant toute la durée du contrat. Cependant la
garantie n'est souvent proposée que jusqu'à un certain âge
(70 ans).
- Enfin, après quelques années
(généralement 2) seul l'assuré a la faculté de
résilier annuellement la police. L'assureur ne peut pas résilier
le contrat.
3.3. Approche utilisés
Comme nous l'avons dit dans le canevas, nous nous proposons de
modéliser une police d'assurance hospitalisation à l'aide d'un
processus en temps continu prenant ses valeurs dans 3 états. Les 3
états sont les suivants :
Pour les hommes :
- Actif
- Hospitalisé suite à une maladie ou un accident
Pour les femmes :
- Actif,
- Hospitalisé suite à une grossesse,
- Hospitalisé pour une autre cause que la grossesse
(accident, maladie)
La finalité de cette approche est d'évaluer les
valeurs des primes nivelées et les montants des provisions.
Généralement, en assurance non vie on utilise
l'approche « fréquence/coûts » dans laquelle
la charge totale annuelle de ministre relative à un assuré serait
modélisé de la manière suivante :

(3.1)
Où N:nombre d'hospitalisation au cours de
l'année ;
Ck : le coût de chaque hospitalisation par
an
Dans ce modèle les couts sont indépendants entre
eux et indépendants du nombre d'hospitalisation.Il existe cependant des
particularités importantes qui rendent le modèle (3.1) peu
adéquate :
- Le coût d'une hospitalisation est très lié
à sa durée. Le nombre d'hospitalisation en un an étant
fonction de la durée d'hospitalisation ainsi l'hypothèse de
l'indépendance entre fréquence et coût semble peu
réaliste.
- La modélisation (3.1) pour tous les âges est
dangereuse dans la mesure où le risque d'hospitalisation augmente
généralement au cours du temps. Pour cela l'assureur doit
provisionner une partie des premières primes pour faire face aux charges
futures.
L'utilisation des processus stochastique est beaucoup plus
appropriée.
3.4. Modélisation
Pour autant qu'on ne différencie pas les causes
d'entrée en hospitalisation et que l'on néglige
l'éventualité d'un décès, l'assurance
hospitalisation se traite de la manière suivante.
Pour les hommes
Ce type de police peut être modélisé
à l'aide d'un processus évoluant dans deux états :
eo= « non hospitalisé ou
actif » et
e1= « hospitalisé »
Hospitalisé
Actif
Fig.3.1. modèles à deux états
décrivant les polices d'assurance hospitalisations pour les
hommes
Pour les femmes
Pour les femmes cependant, il est intéressant de faire
apparaitre explicitement un troisième état, correspondant
à une hospitalisation suite à un accouchement (on tient compte du
délai de carence pour les hospitalisations liées aux grossesses
couvert qu'après 5 mois). Ceci peut être modélisé
à l'aide de 3 états, e0= « active ou
non hospitalisé »,
e1= « hospitalisé » mais pas suite
à une grossesse.
Hospitalisé (sauf grossesse)
Active
Hospitalisé suite à une grosse)
Fig.3.2. modèles à 3 états
décrivant les polices d'assurances hospitalisation pour les
femmes
Nous remarquons que les états des transitions des
hommes sont inclus dans ceux des femmes, c'est pourquoi dans la plupart des
ouvrages traitant des assurances hospitalisation, on s'intéresse aux
polices d'assurances hospitalisation couvrant les femmes. C'est pour cette
raison que nous allons traiter les polices d'assurance hospitalisation couvrant
les femmes.
3.5. Interprétation mathématique des
modèles
Au cours du contrat d'assurance, on ne peut pas prédire
avec exactitude quand est ce que l'assuré sera malade ou en état
de grossesse mais on sait au moins qu'il passera par ces états pendant
une certaine période.
Il s'agit donc d'une expérience aléatoire car on
ne peut pas prédire avec exactitude les résultats mais on connait
à priori tous les résultats possibles (active,
hospitalisé, grossesse). On peut dire que l'assurance constitue une
expérience aléatoire que l'on peut nommer par î, dans
laquelle les états
« active », « hospitalisé », « grossesse »
constituent les éventualités.
Si on note par ? l'ensemble des éventualités
alors nous aurons, ?= {active, hospitalisé, grossesse}.
Comme nous avons un espace d'éventualités ?
relatif à une expérience aléatoire î on peut
définir une ó Algèbre ou une tribu á sur ?.La tribu
á sur ? est un ensemble probabilisable ? (?, á) est un espace
probabilisable.
Comme on ne peut pas connaître avec exactitude la
survenance des états « active »,
« hospitalisé », grossesse » on leurs
associe une mesure de probabilité, nous aurons alors un espace (?,
á, P) qui est l'espace probabilisé.
On remarque alors que l'on peut définir une application
X : ??R, ù?x tel que
i) X(?)={x/ ((existe ù ° ?)/x=X(ù)) est fini et
dénombrable
ii) pout tout x ° R, X-1({x}) ° á
Ceci revient à attribuer une valeur numérique
à chaque résultat possible d'une épreuve
aléatoire.Donc on peut conclure que les différents états
de l'assuré sont des variables aléatoires.
Au cours de la durée de la police, un assuré
passe par plusieurs état schématiser par la survenance ou non
d'un sinistre (grossesse, hospitalisation).
On remarque que chaque événement se produit
à un temps quelconque, si X est l'événement X(t) est cet
événement au temps t. on peut représenter l'espace des
états d'une police quelconque ou pour tout instant t, X(t) donne
l'état ou se trouve l'individu à ce moment.
{X(t), t ° T c R+}, constitue une famille des
variables aléatoire X(t), t°T cR+, définie sur un
même espace probabilisé (?, á, P) et dépendantes du
temps t°T. Cette famille de {X(t), t ° T c R+} constitue un
processus stochastique (aléatoire) ou :
T : est l'espace des instants
X(t) est une réalisation du processus stochastique dans
les différents états
(« active », »hospitalisation », « grossesse »)
C'est pourquoi on introduit également un processus
stochastique {Dt, t=0} décrivant les durées
d'occupation du processus X dans les états e0, e1,
e2.De manière plus formelle Dt=max {z=t/
Xt=Xt-h pour tout 0=h=z}
Formellement l'origine du temps t=0 correspond à la
conclusion du contrat.
On suppose que la police est émise lorsque
l'assurée est dans l'état e0, alors qu'elle est agée de x
années, des sorte que x0=e0.ì
L'événement
« Xt=e0,Dt=z » signifie
que l'assurée est active à l'âge x+t et que la fin de sa
dernière hospitalisation remonte à la date t-z si z<t, ou que
l'assurée est active à l'âge x+t et n'a jamais
été hospitalisée si z=t. L'événement
« Xt=e1,Dt=z » signifie
qu'elle est hospitalisé à l'âge en question depuis une
durée Z et l'événement
« Xt=e2,Dt=z » signifie
qu'elle est hospitalisée suite à une grossesse à
l'âge en question depuis une durée z.
3.6. Taux instantanés des transitions
3.6.1.
Définitions
Les initiales
« a », « h », « g »
sont utilisés pour rappeler les états
« active », « hospitalisé » et
« grossesse ».
Soit ;
- ìah(x+t)  , le taux instantané de transition de l'état e0 vers
l'état e1 à l'âge x+t. la grandeur
ìah(x+t) quantifie le risque pour un individu
âgé de x+t années d'être hospitalisée suite
à une maladie ou un accident. , le taux instantané de transition de l'état e0 vers
l'état e1 à l'âge x+t. la grandeur
ìah(x+t) quantifie le risque pour un individu
âgé de x+t années d'être hospitalisée suite
à une maladie ou un accident.
- ìha(x+t)  , le taux instantané de transition de l'état e1 vers
l'état e0 à l'âge x+t. la grandeur
ìha(x+t) quantifie le risque pour un individu
âgé de x+t années de sortir de l'hôpital après
y être entré pour une maladie ou un accident. , le taux instantané de transition de l'état e1 vers
l'état e0 à l'âge x+t. la grandeur
ìha(x+t) quantifie le risque pour un individu
âgé de x+t années de sortir de l'hôpital après
y être entré pour une maladie ou un accident.
- ìag(x+t)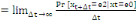  , le taux instantané de transition de l'état e0 vers
l'état e2 à l'âge x+t. la grandeur
ìah(x+t) quantifie le risque pour un individu
âgé de x+t années d'être hospitalisée suite
à une grossesse. , le taux instantané de transition de l'état e0 vers
l'état e2 à l'âge x+t. la grandeur
ìah(x+t) quantifie le risque pour un individu
âgé de x+t années d'être hospitalisée suite
à une grossesse.
- Ìga(x+t)  , le taux instantané de transition de l'état e2 vers
l'état e0 à l'âge x+t. cette grandeur
ìah(x+t) quantifie le risque pour un individu
âgé de x+t de sortir de l'hôpital après y être
entré suite à une grossesse. , le taux instantané de transition de l'état e2 vers
l'état e0 à l'âge x+t. cette grandeur
ìah(x+t) quantifie le risque pour un individu
âgé de x+t de sortir de l'hôpital après y être
entré suite à une grossesse.
Il est à noter que le taux d'hospitalisation suite
à une grossesse ne dépend que de l'âge et pas de la date de
la dernière entrée à l'hôpital pour une
grossesse.
3.6.2. Lien avec
les probabilités de transition
Soit les probabilités de transition entre les instants
s et t, tel que s<p. On peut exprimer les probabilités de transition
entre les différents états de la manière
suivante :
 (3.2) (3.2)
Il s'agit respectivement de la probabilité qu'une
assurée active à l'âge x+s le soit également
à l'âge x+t , qu'une assuré active à l'âge x+s
se retrouve hospitalisée à l'âge x+t, qu'une assurée
active à l'âge x+s se retrouve hospitalisée suite à
une grossesse à l'âge x+t, qu'une assurée
hospitalisée à l'âge x+s soit sortie de l'hôpital
à l'âge x+t, qu'une assurée hospitalisé à
l'âgé x+s le soit également à l'âge x+t,...
Ces probabilités fixent les états occupés
aux instants s et t.
3.6.3. Expression
des probabilités de transition sous forme de taux de transition
Le taux de transition peut se voir comme des
dérivées partielles des probabilités de transition par
rapport au temps imparti pour effectuer le parcours requis
 (3.3) (3.3)
Par conséquence un développement de Taylor
limité au premier ordre donne les expressions suivantes :
 (3.4) (3.4)
3.7. Constance des taux instantanés de transition
Hypothèse
Nous supposons les taux instantanés de transition
constat à chaque âge, c.à.d. quels que soient l'âge x
entier et 0=t=1, les identités suivantes
(3.5)
ìah(x+t)= ìah(x),
ìag(x+t)= ìag(x),
ìha(x+t)= ìha(x),
ìga(x+t)= ìga(x),
sont vérifiées.
3.7.1.
Probabilité de transition annuelle
Commençons par estimer t  en fonction des taux. Partons de l'expression suivante : en fonction des taux. Partons de l'expression suivante :
t+Ät  =Pr[ =Pr[  + +  =e0], étant donné que e0,e1,e2 forment un système
complet d'évenement et que pour un evenement ek avec k°{0,1,2}, un
autre événement ej={0,1,2} ne peut se produire qu'en combinaison
avec l'un de ek du système complet. On applique le
théorème de probabilité totale. =e0], étant donné que e0,e1,e2 forment un système
complet d'évenement et que pour un evenement ek avec k°{0,1,2}, un
autre événement ej={0,1,2} ne peut se produire qu'en combinaison
avec l'un de ek du système complet. On applique le
théorème de probabilité totale.
e0= 
ce qui donne:
Pr[  =e0| =e0|  =e0]= Pr[ =e0]= Pr[  =e0| =e0|  =e0]. Pr[ =e0]. Pr[  =e0| =e0|  =e0]+ Pr[ =e0]+ Pr[  =e1| =e1|  =e0] Pr[ =e0] Pr[  =e0| =e0|  =e1]+ =e1]+
[  =e2| =e2|  =e0]. Pr[ =e0]. Pr[  =e0| =e0|  =e2], =e2],
En se référant à (3.2),
Pr[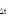  =e0| =e0|  =e0]=t =e0]=t  Ät. Ät.  + t + t  Ät. Ät.  + t + t  Ät. Ät. 
Considérons à présent un âge x
entier, un instant 0<t<1 et un accroissement Ät tel que t+
Ät<1. Nous pouvons alors écrire en se référant
à (3.4)
t+Ät   = t = t  (1-( ìah(x)+ ìag(x)) Ät)+ t (1-( ìah(x)+ ìag(x)) Ät)+ t  ìha(x) Ät+ t ìha(x) Ät+ t  ìga(x) Ät+o(Ät) ìga(x) Ät+o(Ät)
avec o(Ät) :notation de Landau, une fonction
arbitraire de Ät tel que   =0 , ou Ät est un infiniment petit d'ordre supérieur
à Ät. =0 , ou Ät est un infiniment petit d'ordre supérieur
à Ät.
Ceci donne, t+Ät   = t = t  -(( ìah(x)+ ìag(x)) -(( ìah(x)+ ìag(x))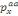  + t + t  ìha(x) + t ìha(x) + t  ìga(x) )Ät+o(Ät) ìga(x) )Ät+o(Ät)
?
  =-( ìah(x)+ ìag(x)) =-( ìah(x)+ ìag(x))  + t + t  ìha(x) + t ìha(x) + t  ìga(x) + ìga(x) + 
Par passage à la limite pour  , on obtient l'équation suivant , on obtient l'équation suivant
  -( ìah(x)+ ìag(x)) -( ìah(x)+ ìag(x))  + t + t  ìha(x) + t ìha(x) + t  ìga(x) (3.6) ìga(x) (3.6)
En procèdent de la même manière on
obtient les équations différentielles suivantes pour les autres
probabilités de transition.
 (3 .7) (3 .7)
Il est simple de résoudre le système
intégro-différentiel de l'ensemble des probabilités de
transition en utilisant une écriture matricielle. En effet introduisant
la matrice Mx reprenant les taux de transition entre paires d'états hors
de la diagonale principale, et l'opposé de la somme des
éléments de la ligne correspondante sur la diagonale
Mx=  
En notant Px(t)=  
Il vient alors que le système (3.7) peut s'écrire
  Px(t)=Px(t) Mx (3.8), Px(t)=Px(t) Mx (3.8),
où la dérivée d'une matrice peut se
comprendre comme la matrice de dérivées. La solution de cette
équation est donnée par la série  
En calculant 3.8 par la méthode de Cox et Miller, en
supposant que Mx possède 3 valeurs propres distinctes  , ,   et et   comme Mx est de rang inférieur ou égal à deux,
l'une des valeurs propres est nécessairement nulle. Le vecteur propre
associé à cette valeur propre est colinéaire au vecteur
(1, 1, 1) T. comme Mx est de rang inférieur ou égal à deux,
l'une des valeurs propres est nécessairement nulle. Le vecteur propre
associé à cette valeur propre est colinéaire au vecteur
(1, 1, 1) T.
Supposons par exemple que   =0, on peut ensuite décomposer Mx comme, =0, on peut ensuite décomposer Mx comme,
Mx=Axdiag (  , ,   et et   ) représente une matrice diagonale 3*3. ) représente une matrice diagonale 3*3.
Dès lors
Px(t)=Ax  + + 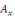 diag ( diag (  , ,   et et   ) )  + +  diag ( diag (  , ,  , ,  ) )  +... +...
=  diag ( diag (  , ,   , ,  ) ) 
=  diag (exp diag (exp 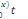 ), exp ), exp  ), exp ), exp  )) )) 
3.8. Lien avec les probabilités de séjour
3.8.1.
Définition
Les probabilités de séjour sont les
probabilités d'occuper sans arrêt un état entre les
instants s et t. Ces probabilités dans les différent états
sont données par
t-s 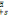 =Pr[XT=e0 pour tout s<T<t /Xs=e0] =Pr[XT=e0 pour tout s<T<t /Xs=e0]
= Pr[XT=e0 et DT=t-s pour tout s<T<t
/Xs=e0]
t-s  =Pr[XT=e1 pour tout s<T<t /Xs=e1] =Pr[XT=e1 pour tout s<T<t /Xs=e1]
= Pr[XT=e1 et DT=t-s pour tout s<T<t /Xs=e1]
t-s  =Pr[XT=e2 pour tout s<T<t /Xs=e2] =Pr[XT=e2 pour tout s<T<t /Xs=e2]
= Pr[XT=e2 et DT=t-s pour tout s<T<t /Xs=e2]
Avec DT la durée d'occupation d'un individu
dans l'état a,h,g
3.8.2. Expression
des probabilités de séjour en fonction des taux des
transitions
On peut également exprimer les probabilités de
séjour en fonction des taux des transitions. Pour obtenir l'expression
de t  en fonction des taux des transitions, partons de l'expression suivante
obtenu en conditionnant par rapport à l'état occupé par
l'assuré entre les instants s et t. en fonction des taux des transitions, partons de l'expression suivante
obtenu en conditionnant par rapport à l'état occupé par
l'assuré entre les instants s et t.
t+Ät  = t = t  t.Ät t.Ät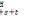  en se referant à (3.4), on peut écrire en se referant à (3.4), on peut écrire
t+Ät  = t = t  [1-( ìah(x+s+t)+
ìag(x+s+t))Ät+o(Ät)] en posant [1-( ìah(x+s+t)+
ìag(x+s+t))Ät+o(Ät)] en posant
ìah(x+s+t)+ ìag(x+s+t)=
ìa.(x+s+t)
on a t+Ät  = t = t  [1- ìa.(x+s+t)Ät+ o(Ät)] [1- ìa.(x+s+t)Ät+ o(Ät)]
ce qui donne   t t  . ìa.(x+s+t)Ät+ . ìa.(x+s+t)Ät+ 
En passant à la limite pour   ?0, on obtient l'équation différentielle ?0, on obtient l'équation différentielle
  t t  . ìa.(x+s+t) . ìa.(x+s+t)
A la condition initiale t=0, ou à   =1, l'équation différentiel possède comme solution
satisfaisant les conditions initial, =1, l'équation différentiel possède comme solution
satisfaisant les conditions initial,
t  =exp(- =exp(-  )+ )+  )dô) )dô)
on vérifie aussi de la même façon
que :
t  =exp(- =exp(-  )dô) )dô)
t  =exp(- =exp(-  )dô) )dô)
3.9. Aspects techniques
3.9.1. Prestations
des parties
3.9.1.1. Clauses particulières
Comme annoncé dans l'introduction, la plupart des
polices prévoit un délai de carence pour l'accouchement,
noté ãg. ceci signifie que l'hospitalisation
liées à des grossesses survenant durant [0, ãg]
ne seront pas indemnisées par l'assureur. On peut également
produire des franchises temporelles fg et fh qui sont des
durées d'hospitalisation minimales avant indemnisation.
3.9.1.2. Paiement des primes
Le paiement des primes est décrit par la fonction   (.) représentant le montant cumulé payé par
l'assuré au cours du temps. Ainsi (.) représentant le montant cumulé payé par
l'assuré au cours du temps. Ainsi   (t) représente le montant payé par l'assuré sur
l'intervalle [0,t]. La fonction Ð est non décroissante et continue
à gauche, il satisfait donc la condition (t) représente le montant payé par l'assuré sur
l'intervalle [0,t]. La fonction Ð est non décroissante et continue
à gauche, il satisfait donc la condition
  (t) = (t) =  (t) = (t) =  pour tout t. pour tout t.
  ( (  ) = ) =  représente le montant de la prime payée à la
souscription de la police, et les primes ne sont dues que lorsque
l'assuré est hospitalisée. Par conséquent, la valeur
actuelle moyenne des primes payées sur [0,t] vaut représente le montant de la prime payée à la
souscription de la police, et les primes ne sont dues que lorsque
l'assuré est hospitalisée. Par conséquent, la valeur
actuelle moyenne des primes payées sur [0,t] vaut
E[  = =  en appliquant les principes de l'équivalence on obtient la prime
souscrit par un assuré à l'âge x pour une durée de
contrat n ; en appliquant les principes de l'équivalence on obtient la prime
souscrit par un assuré à l'âge x pour une durée de
contrat n ;

Ou :
- v(t) est la valeur actuelle d'une somme payable à
l'instant t pour être en mesure de couvrir un sinistre s'il arrive
à cet instant.
En raison des franchises temporelles, aucune indemnité
ne sera versée en cas d'hospitalisation entre les instants
n-fg v fh et n ; ou n est la durée du
contrat
fg v fh=inf{ fg, fh}
La quantité  représente la prime unique pure à verser pour un contrat
d'assurance de durée n. représente la prime unique pure à verser pour un contrat
d'assurance de durée n.
3.9.1.3. Prestation de l'assureur
Le cout journalier des hospitalisations est aléatoire
si le contrat est indemnitaire (car il dépend du type de pathologie, des
complications éventuelles, etc...) et est connu si le contrat est
forfaitaire. Afin d'obtenir une écriture homogène pour les 2
types de contrat, on travaillera sur le contrat indemnitaires avec un
coût moyen par journée d'hospitalisation.
- Nous supposons que les coûts peuvent être
décrits par des fonctions
(t,v)?Bh(t,v) et (t,v)?Bg(t,v)
définie pour t=v, représentant les montant cumulés
payés à l'assurés sur l'intervalle [t-v,t ] si elle a
été hospitalisée à la date t-v et est resté
à l'hôpital jusqu'à la date t.
Notons : Bi (t) avec i=h,g. le montant
payé par l'assureur sur un intervalle quelconque à
préciser. Elle est décroissante et continue à gauche. On
suppose également que l'inflation des coûts est comprise dans
Bi afin d'anticiper les évolutions futur des couts des
soins.
La fonction B(t) possède un différentiel dB de la
forme suivante dB=b (t)dt+ÄB (t), ou b est une fonction non
négative car elle est différentiable par morceau. Le montant
actualisé et versé à l'assuré en hospitalisation
à l'instant t sur un intervalle [0,t]
- Nous supposons implicitement que les taux des transitions
prennent en compte l'évolution future attendue des fréquences
d'hospitalisation,
Alors pour tout t=s>0, les fonctions t?Bh(t,t-s)
et t?Bg(t,t-s) se decomposent en une partie absolument continue et
des sauts :
d Bh(t,t-s)= bh(t,t-s)dt+ Ä
Bh(t,t-s)
d Bg(t,t-s)= bg(t,t-s)dt+ Ä
Bg(t,t-s)
ou Ä Bh(t,t-s)= Bh(t+,(t+)-s)-
Bh(t,t-s) et Ä Bg(t,t-s)= Bg(t+,(t+)-s)-
Bg(t,t-s)
ainsi Ä Bg(t,t-s) représente la somme
versée juste après l'instant t à l'assurée qui se
trouve hospitalisée pour une grossesse à cet instant depuis une
durée t-s.
En pratique dans la plupart des cas, nous supposons que
l'assureur rembourse l'intégralité des frais d'hospitalisation,
c'est pourquoi v(t) dans la pratique sera le montant des dépenses lors
de la prise en charge à l'hôpital.
La valeur actuelle moyenne des prestations versés par
l'assureur sur [0,t] est donnée par :
E[  ]+ E[ ]+ E[  ] ]
= 

3.9.2.
Réserves mathématiques
A tout instant l'assureur devra disposer d'une provision
représentant la part de prestations futures non couvertes par les primes
restant à échoir. Cette provision dépendra de
l'état occupé par l'assuré à l'instant t et, si
l'individu est hospitalisé, de la durée passé dans cet
état. Nous aurons ainsi les réserves
Va(t),Vh(t,d) et Vg(t,d) selon que
l'assurée est active, hospitalisée depuis une durée d, ou
hospitalisée par accouchement depuis une durée d.
- Pour une assurée active, désignons par n la
durée maximale de l'engagement de l'assureur
Va(t)= E[  ]+ E[ ]+ E[  ]- E[ ]- E[  ] ]
Dans le cas particulier ou les fonctions de paiement ne
dépendent pas de la durée d'hospitalisation, nous avons pour une
assurée active à l'instant t>ãg (delai de
carence)
Va(t)=  + +  - - 
- Pour une assurée hospitalisée nous avons,
Vh(t,d)= E[  ]+ E[ ]+ E[  ]- E[ ]- E[  ] ]
Dans le cas particulier ou les fonctions de paiement ne
dépendent pas de la durée d'hospitalisation, nous avons pour une
assurée hospitalisée à l'instant
t>ãg (delai de carence)
Vh(t)=  + +  - - 
- Pour une assurée hospitalisée pour un
accouchement
La reserve Vg(t) s'ontient de la même
manière que ci haut, nous avons
Vg(t)=  + +  - - 
3.10. Estimation des taux de
transition
3.10.1. Exposition au risque
L'exposition au risque est le temps vécu par un
individu entre l'âge x et l'âge x+1
L'exposition au risque dans l'état actif à
l'âge x (ou années révolues) vaut :
ERa(x)=temps total passé en activité
par les femmes d'âge x au cours d'une période
ERa(x)=  , ou , ou 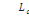  désigne le nombre des femmes ayant occupé l'état
« actif » à l'âge x, et désigne le nombre des femmes ayant occupé l'état
« actif » à l'âge x, et   la durée d'activité de la ième
femme. la durée d'activité de la ième
femme.
L'exposition du risque dans l'état
hospitalisé
Elle vaut ERh(x)=temps total passé à
l'hôpital par les femmes d'âge x au cours d'une période
ERh(x)=  , ou , ou   désigne le nombre des femmes ayant effectué un
séjour à l'hopital à l'âge x, et désigne le nombre des femmes ayant effectué un
séjour à l'hopital à l'âge x, et   la durée d'hospitalisation de la IVème
femme. la durée d'hospitalisation de la IVème
femme.
L'exposition du risque dans l'état hospitalisé
pour un accouchement
Cette exposition vaut
ERg(x)=temps total passé à
l'hôpital pour un accouchement par les femmes d'âge x au cours
d'une période
ERg(x)=  , ou , ou   désigne le nombre des femmes ayant effectué un
séjour à l'hopital suite à une grossesse à
l'âge x, et désigne le nombre des femmes ayant effectué un
séjour à l'hopital suite à une grossesse à
l'âge x, et   la durée d'hospitalisation de la ième
femme. la durée d'hospitalisation de la ième
femme.
3.10.2. Estimation brut des taux de transition
On dispose pour un grand nombre de femmes leurs observations
sur une ou plusieurs années, les temps de séjour dans les
différents états (temps écoulé entre transition
successives et nombre de transitions de chaque type)
Soit   , ,  , ,  , ,  le risque relatifs pour un assuré d'âge x d'être
dans un état d'hospitalisation, d'activité ou d'accouchement. La
fonction de vraisemblance relatif à cet observation est L( le risque relatifs pour un assuré d'âge x d'être
dans un état d'hospitalisation, d'activité ou d'accouchement. La
fonction de vraisemblance relatif à cet observation est L(  , ,  , ,  , ,  (x)). (x)).
Chaque période de durée Ät passé par
un assuré d'âge x dans l'état « actif »
contribue à hauteur d'un facteur exp(-(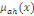  + +  ), la même période passé à l'état
hospitalisé à hauteur de exp(- ), la même période passé à l'état
hospitalisé à hauteur de exp(-  Ät ) et enfin dans l'état accouchement à hauteur de
exp(- Ät ) et enfin dans l'état accouchement à hauteur de
exp(-  Ät). Ät).
Chaque passage de e0 à e1, de e1 à e2, de e1
à e0 et de e2 à e0 contribue respectivement à la
vraisemblance à hauteur d'un facteur  , d'un facteur , d'un facteur  , d'un facteur , d'un facteur   et enfin d'un facteur et enfin d'un facteur  . .
Il faut mémoriser la durée totale passée
par les assurées dans les différents états en
répertoriant les expositions et le nombre de transition
effectuées par ces assurées.
Notons alors,
  : le nombre de transition de l'état actif à celui
d'hospitalisé effectué par l'assuré j d'âge x. : le nombre de transition de l'état actif à celui
d'hospitalisé effectué par l'assuré j d'âge x.
  : le nombre de transition de l'état hospitalisé à
celui d'actif effectué par l'assuré j d'âge x. : le nombre de transition de l'état hospitalisé à
celui d'actif effectué par l'assuré j d'âge x.
  : le nombre de transition de l'état actif à celui
d'hospitalisé pour une grossesse effectué par l'assuré j
d'âge x. : le nombre de transition de l'état actif à celui
d'hospitalisé pour une grossesse effectué par l'assuré j
d'âge x.
  : le nombre de transition de l'état hospitalisé pour une
grossesse à l'état actif effectué par l'assuré j
d'âge x. : le nombre de transition de l'état hospitalisé pour une
grossesse à l'état actif effectué par l'assuré j
d'âge x.
Posons   = =  , ,  = =  , ,  = =  , ,  = = 
Les observations relatives à ces variables sont  , ,  , ,  , , 
La fonction de vraisemblance associée à un individu
d'âge fixe peut s'écrire
L(  , ,  , ,  , ,  (x))= exp[-( (x))= exp[-(  + +  ]. exp[-( ]. exp[-(  ]. ].
exp[-(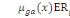  ] ]   (3.9) (3.9)
En passant à la log de vraisemblance, puis en annulant les
dérivées partielles par rapport aux quatre paramètres   , ,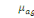  , ,  , ,  (x), il vient (x), il vient
  ; ;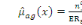  ; ;  ; ;  sont des estimateurs de maximum de vraisemblance non contraints, ou
brut, des taux instantanés de transition entre différents
états de figure Fig3.2. sont des estimateurs de maximum de vraisemblance non contraints, ou
brut, des taux instantanés de transition entre différents
états de figure Fig3.2.
Chapitre 4 :
Estimation de la prime de risque pour une prise en charge
dans les services de
maternité et de Gynéco au l'hôpital
Saint joseph de
Kinshasa
Introduction
Dans ce chapitre, nous allons faire des estimations des
différentes variables statistique en vue de calculer la prime de risque
à verser par une assurée qui fréquente un milieu
hospitalier pour une prise en charge adéquate en cas de problème
de santé.
Suite à des difficultés ressenties pour la
récolte des données dans des hôpitaux concernant certaines
informations dites sensibles et en ajoutant aux difficultés
citées, la quasi inexistence des services statistique ; nous
étions obliger de constituer nous même par l'interview, les
questionnaires d'enquête et la technique documentaire notre
échantillon.
La lourdeur de ces travaux à fait à ce que notre
étude à porter sur la maternité et la gynécologie,
au lieu de porter sur tous les services de l'hôpital.
L'échantillon est constitué de 465 observations des individus de
15 à 47 ans pour un toutes les pathologies ou les complications possible
concernant la gynécologie-obstétrique dont 300
échantillons 15 à 47 ans pour la maternité. Cet
étude s'intéresse à la prise en charge des patientes pour
les premiers soins en cas d'une attaque dangereuse pour la santé et qui
exige une intervention immédiate des services médicales. Selon
les informations recueillies sur place les cas de malades deviennent souvent
fatals à cause de retard de paiement de frais de prise en charge
permettant un accès immédiat aux soins appropriés.
C'est pourquoi, nous nous sommes intéressés
à cette étape de prise en charge clinique. Les traitements des
maladies ne sont pas vraiment aborder dans notre travail. Nous
considérons que la patiente qui arrive à l'hôpital dans une
situation difficile doit être capable de recevoir les premiers soins, de
faire l'objetdes examens de laboratoire, de faire l'objet d'une consultation
médicale auprès d'un médecins, d'une observation et
même d'une prise en charge avec internement pour des durées allant
jusqu'à 3 jours.
Donc le but de notre travail réalisé à
l'hôpital Saint Joseph, consiste à mettre en place une petite
Société d'assurance Maladie (Prise en charge d'urgence) des
femmes qui viennent en urgence en maternité pour un accouchement (pour
les accouchement la prise en charge est totale) ou pour une complication qui
atteint leurs intégrités physiques. Dans ce dernier cas la prise
en charge peut être totale (Crise d'anémie) ou partielle (Menace
d'avortement) qui doit être suivie des soins de traitement.
Après la récolte des données nous avions
pu réunir des informations dont nous avons besoins pour notre
étude, ces informations sont notamment :
· L'âge de la patiente ;
· La durée d'hospitalisation, nous rappelons que ce
n'est pas la durée de traitement de la maladie mais un temps
d'observation de la patiente qui peut aller de quelques heures à trois
jours. Dans le cadre de notre étude toutes observations ou toute prise
en charge de moins de 24 heures sont considérer comme des durées
d'hospitalisation de 24heures.
· Les montants (Frais) des prises en charge.
· Une estimation des nombres de manifestation possible de la
même crise (pathologie) au cours de l'année.
Ces données de base nous permettront de calculer les
statistiques intermédiaires pour notre étude. Les données
récoltées se trouve en annexe A ; nous n'y avions mis que
les données synthétisé à cause de la grande
quantité des données brutes.
3.10.3. Estimations de nombre de transition de l'état
« actif » à l'état
« grossesse » (« accouchement »)
Pour estimer le nombre de transition nous avons
généré avec SPSS un tableau croisé des
durées d'hospitalisation en fonction des âges des patientes.
A partir de ce tableau nous pouvons calculer les nombres de
transition de l'état hospitalisé à l'état
grossesse.
Tableau.4. Nombre des transitions de l'état
« actif » à l'état
« accouchement »
|
Transition
|
|
|
Age
|
0,25
|
0,3
|
0,5
|
|
|
15
|
0
|
0
|
1
|
0,5
|
|
16
|
0
|
0
|
2
|
1
|
|
17
|
0
|
0
|
1
|
0,5
|
|
18
|
0
|
0
|
2
|
1
|
|
19
|
0
|
0
|
4
|
2
|
|
20
|
0
|
0
|
5
|
2,5
|
|
21
|
0
|
0
|
8
|
4
|
|
22
|
0
|
0
|
6
|
3
|
|
23
|
0
|
0
|
11
|
5,5
|
|
24
|
0
|
0
|
3
|
1,5
|
|
25
|
0
|
0
|
6
|
3
|
|
26
|
0
|
0
|
11
|
5,5
|
|
27
|
0
|
0
|
6
|
3
|
|
28
|
0
|
0
|
8
|
4
|
|
29
|
0
|
2
|
1
|
1,1
|
|
30
|
0
|
7
|
0
|
2,1
|
|
31
|
1
|
4
|
3
|
2,95
|
|
32
|
0
|
6
|
1
|
2,3
|
|
34
|
1
|
2
|
1
|
1,35
|
|
35
|
5
|
2
|
1
|
2,35
|
|
36
|
3
|
1
|
0
|
1,05
|
|
37
|
6
|
0
|
0
|
1,5
|
|
38
|
3
|
0
|
1
|
1,25
|
|
39
|
1
|
0
|
0
|
0,25
|
|
40
|
3
|
0
|
0
|
0,75
|
|
42
|
1
|
0
|
0
|
0,25
|
Selon ce tableau, par exemple pour la première ligne,
une seule femme de 15 ans fait 0,5 transition par an, c'est-à-dire
qu'à partir des observations faites sur notre échantillon une
seule femme de 15 ans sur le 140 à la possibilité d'accoucher 1
fois tous les 2 ans.
Pour estimer le temps total passé à
l'hôpital par les femmes d'un certain âge nous
générons le tableau croisé des durées
d'hospitalisation en fonction de l'âge. Ce tableau nous permettra de
calculer l'exposition au risque dans l'état
« grossesse ».
Tableau.5. Exposition au risque dans l'état
« grossesse ».
|
Durée
|
|
|
Age
|
3
|
|
|
15
|
1
|
3
|
|
16
|
2
|
6
|
|
17
|
1
|
3
|
|
18
|
2
|
6
|
|
19
|
4
|
12
|
|
20
|
5
|
15
|
|
21
|
8
|
24
|
|
22
|
6
|
18
|
|
23
|
11
|
33
|
|
24
|
3
|
9
|
|
25
|
6
|
18
|
|
26
|
11
|
33
|
|
27
|
6
|
18
|
|
28
|
8
|
24
|
|
29
|
3
|
9
|
|
30
|
7
|
21
|
|
31
|
8
|
24
|
|
32
|
7
|
21
|
|
33
|
10
|
30
|
|
34
|
4
|
12
|
|
35
|
8
|
24
|
|
36
|
4
|
12
|
|
37
|
6
|
18
|
|
38
|
4
|
12
|
|
39
|
1
|
3
|
|
40
|
3
|
9
|
|
42
|
1
|
3
|
Pour calculer l'exposition au risque à l'état
« actif » on fait le tableau croisé de durée
d'activité en fonction des âges. On obtient le tableau suivant.
Tableau.6. Exposition au risque dans
l'état « actif ».
|
Tableau croisé Age * Activité
|
|
|
Activité
|
|
|
Age
|
358,5
|
359,1
|
359,25
|
|
|
15
|
1
|
0
|
0
|
358,5
|
|
16
|
2
|
0
|
0
|
717
|
|
17
|
1
|
0
|
0
|
358,5
|
|
18
|
2
|
0
|
0
|
717
|
|
19
|
4
|
0
|
0
|
1434
|
|
20
|
5
|
0
|
0
|
1792,5
|
|
21
|
8
|
0
|
0
|
2868
|
|
22
|
6
|
0
|
0
|
2151
|
|
23
|
11
|
0
|
0
|
3943,5
|
|
24
|
3
|
0
|
0
|
1075,5
|
|
25
|
6
|
0
|
0
|
2151
|
|
26
|
11
|
0
|
0
|
3943,5
|
|
27
|
6
|
0
|
0
|
2151
|
|
28
|
8
|
0
|
0
|
2868
|
|
29
|
1
|
2
|
0
|
1076,7
|
|
30
|
0
|
7
|
0
|
2513,7
|
|
31
|
3
|
4
|
1
|
2871,15
|
|
32
|
1
|
6
|
0
|
2513,1
|
|
33
|
0
|
10
|
0
|
3591
|
|
34
|
1
|
2
|
1
|
1435,95
|
|
35
|
1
|
2
|
5
|
2872,95
|
|
36
|
0
|
1
|
3
|
1436,85
|
|
37
|
0
|
0
|
6
|
2155,5
|
|
38
|
1
|
0
|
3
|
1436,25
|
|
39
|
0
|
0
|
1
|
359,25
|
|
40
|
0
|
0
|
3
|
1077,75
|
|
42
|
0
|
0
|
1
|
359,25
|
|
|
|
|
50228,4
|
Tableau.7. Nombre de transition de l'état
« grossesse » à l'état
« actif »
|
Tableau croisé Age * Transition ga
|
|
|
|
|
|
|
|
Transition ga
|
|
|
Age
|
0,25
|
0,3
|
0,5
|
|
|
15
|
0
|
0
|
1
|
0,5
|
|
16
|
0
|
0
|
2
|
1
|
|
17
|
0
|
0
|
1
|
0,5
|
|
18
|
0
|
0
|
2
|
1
|
|
19
|
0
|
0
|
4
|
2
|
|
20
|
0
|
0
|
5
|
2,5
|
|
21
|
0
|
0
|
8
|
4
|
|
22
|
0
|
0
|
6
|
3
|
|
23
|
0
|
0
|
11
|
5,5
|
|
24
|
0
|
0
|
3
|
1,5
|
|
25
|
0
|
0
|
6
|
3
|
|
26
|
0
|
0
|
11
|
5,5
|
|
27
|
0
|
0
|
6
|
3
|
|
28
|
0
|
0
|
8
|
4
|
|
29
|
0
|
3
|
0
|
0,9
|
|
30
|
0
|
7
|
0
|
2,1
|
|
31
|
0
|
8
|
0
|
2,4
|
|
32
|
0
|
7
|
0
|
2,1
|
|
33
|
0
|
10
|
0
|
3
|
|
34
|
4
|
0
|
0
|
1
|
|
35
|
8
|
0
|
0
|
2
|
|
36
|
4
|
0
|
0
|
1
|
|
37
|
6
|
0
|
0
|
1,5
|
|
38
|
4
|
0
|
0
|
1
|
|
39
|
1
|
0
|
0
|
0,25
|
|
40
|
3
|
0
|
0
|
0,75
|
|
42
|
1
|
0
|
0
|
0,25
|
Nous pouvons maintenant estimer le taux de transition de
l'état « actif » à l'état
« grossesse »
Tableau.8. Estimation des taux de transition  de l'état « actif » à l'état
« grossesse ». de l'état « actif » à l'état
« grossesse ».
|
Age
|
|
|
|
|
15
|
358,5
|
0,5
|
0,0013947
|
|
16
|
717
|
1
|
0,0013947
|
|
17
|
358,5
|
0,5
|
0,0013947
|
|
18
|
717
|
1
|
0,0013947
|
|
19
|
1434
|
2
|
0,0013947
|
|
20
|
1792,5
|
2,5
|
0,0013947
|
|
21
|
2868
|
4
|
0,0013947
|
|
22
|
2151
|
3
|
0,0013947
|
|
23
|
3943,5
|
5,5
|
0,0013947
|
|
24
|
1075,5
|
1,5
|
0,0013947
|
|
25
|
2151
|
3
|
0,0013947
|
|
26
|
3943,5
|
5,5
|
0,0013947
|
|
27
|
2151
|
3
|
0,0013947
|
|
28
|
2868
|
4
|
0,0013947
|
|
29
|
1076,7
|
1,1
|
0,00102164
|
|
30
|
2513,7
|
2,1
|
0,00083542
|
|
31
|
2871,15
|
2,95
|
0,00102746
|
|
32
|
2513,1
|
2,3
|
0,0009152
|
|
33
|
3591
|
3
|
0,00083542
|
|
34
|
1435,95
|
1,35
|
0,00094014
|
|
35
|
2872,95
|
2,35
|
0,00081797
|
|
36
|
1436,85
|
1,05
|
0,00073077
|
|
37
|
2155,5
|
1,5
|
0,00069589
|
|
38
|
1436,25
|
1,25
|
0,00087032
|
|
39
|
359,25
|
0,25
|
0,00069589
|
|
40
|
1077,75
|
0,75
|
0,00069589
|
|
42
|
359,25
|
0,25
|
0,00069589
|

Graph1. Représentation graphique des taux ag de
transition en fonction de l'âge.
Nous remarquons qu'au environ de 27 ans le taux de transition
décroit considérablement jusqu'à 30 ans pour se
stabiliser enfin de 38ans. Ceci explique par la diminution des femmes en
activité d'accouchement, on a de moins en moins des femmes qui viennent
accoucher à partir de 28 ans dans notre échantillon.
Nous pouvons maintenant estimer le taux de transition de
l'état « grossesse » à l'état
« actif»
Tableau.10. Estimation des taux de transition  de l'état « actif » à l'état
grossesse. de l'état « actif » à l'état
grossesse.
|
Age
|
|
|
|
|
15
|
3
|
0,5
|
0,16666667
|
|
16
|
6
|
1
|
0,16666667
|
|
17
|
3
|
0,5
|
0,16666667
|
|
18
|
6
|
1
|
0,16666667
|
|
19
|
12
|
2
|
0,16666667
|
|
20
|
15
|
2,5
|
0,16666667
|
|
21
|
24
|
4
|
0,16666667
|
|
22
|
18
|
3
|
0,16666667
|
|
23
|
33
|
5,5
|
0,16666667
|
|
24
|
9
|
1,5
|
0,16666667
|
|
25
|
18
|
3
|
0,16666667
|
|
26
|
33
|
5,5
|
0,16666667
|
|
27
|
18
|
3
|
0,16666667
|
|
28
|
24
|
4
|
0,16666667
|
|
29
|
9
|
0,9
|
0,1
|
|
30
|
21
|
2,1
|
0,1
|
|
31
|
24
|
2,4
|
0,1
|
|
32
|
21
|
2,1
|
0,1
|
|
33
|
30
|
3
|
0,1
|
|
34
|
12
|
1
|
0,08333333
|
|
35
|
24
|
2
|
0,08333333
|
|
36
|
12
|
1
|
0,08333333
|
|
37
|
18
|
1,5
|
0,08333333
|
|
38
|
12
|
1
|
0,08333333
|
|
39
|
3
|
0,25
|
0,08333333
|
|
40
|
9
|
0,75
|
0,08333333
|
|
42
|
3
|
0,25
|
0,08333333
|

Graph2. Représentation graphique des taux de
transition ga en fonction de l'âge.
3.11. Service de Gynécologie
3.11.1. Estimations de nombre de transition de l'état
« actif » à l'état
« hospitalisé »
Pour estimer le nombre de transition nous avons
généré avec SPSS un tableau croisé des
durées d'hospitalisation en fonction des âges.
De ce tableau nous pouvons calculer les nombres de transition de
l'état actif à l'état hospitalisé.
Tableau.11. Nombre des transitions de l'état
« actif » à l'état
« hospitalisé »
|
Tableau croisé Age * Transition
|
|
|
Transition
|
|
|
Age
|
0,3
|
0,5
|
0,8
|
1
|
2
|
3
|
4
|
5
|
|
|
15
|
0
|
1
|
0
|
1
|
1
|
0
|
2
|
3
|
26,5
|
|
16
|
0
|
3
|
0
|
3
|
0
|
0
|
1
|
1
|
13,5
|
|
17
|
1
|
7
|
0
|
1
|
0
|
1
|
3
|
5
|
44,8
|
|
18
|
0
|
4
|
0
|
2
|
0
|
0
|
2
|
2
|
22
|
|
19
|
1
|
4
|
0
|
2
|
1
|
0
|
5
|
3
|
41,3
|
|
20
|
1
|
3
|
0
|
3
|
0
|
0
|
5
|
2
|
34,8
|
|
21
|
1
|
4
|
0
|
3
|
0
|
1
|
0
|
2
|
18,3
|
|
22
|
0
|
6
|
0
|
4
|
0
|
1
|
2
|
3
|
33
|
|
23
|
0
|
4
|
0
|
0
|
0
|
0
|
3
|
1
|
19
|
|
24
|
0
|
2
|
0
|
3
|
0
|
0
|
0
|
3
|
19
|
|
25
|
1
|
6
|
0
|
1
|
0
|
0
|
4
|
3
|
35,3
|
|
26
|
1
|
4
|
0
|
4
|
0
|
0
|
1
|
1
|
15,3
|
|
27
|
0
|
11
|
0
|
3
|
0
|
0
|
3
|
2
|
30,5
|
|
28
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
5
|
33,8
|
|
29
|
0
|
2
|
0
|
2
|
0
|
1
|
3
|
0
|
18
|
|
30
|
1
|
2
|
0
|
4
|
0
|
0
|
4
|
1
|
26,3
|
|
31
|
1
|
5
|
0
|
2
|
0
|
0
|
0
|
3
|
19,8
|
|
32
|
2
|
1
|
0
|
2
|
0
|
1
|
0
|
1
|
11,1
|
|
33
|
2
|
6
|
0
|
1
|
0
|
0
|
2
|
2
|
22,6
|
|
34
|
0
|
5
|
0
|
0
|
0
|
1
|
1
|
2
|
19,5
|
|
35
|
1
|
6
|
0
|
4
|
0
|
0
|
4
|
1
|
28,3
|
|
36
|
0
|
4
|
0
|
1
|
0
|
0
|
1
|
0
|
7
|
|
37
|
3
|
3
|
0
|
3
|
0
|
0
|
4
|
7
|
56,4
|
|
38
|
0
|
3
|
0
|
0
|
0
|
0
|
0
|
4
|
21,5
|
|
39
|
0
|
1
|
0
|
5
|
0
|
0
|
6
|
0
|
29,5
|
|
40
|
0
|
1
|
0
|
0
|
0
|
1
|
5
|
1
|
28,5
|
|
41
|
1
|
0
|
0
|
1
|
1
|
0
|
2
|
0
|
11,3
|
|
42
|
1
|
2
|
0
|
1
|
0
|
0
|
1
|
1
|
11,3
|
|
43
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
10,3
|
|
44
|
2
|
1
|
0
|
0
|
0
|
0
|
2
|
0
|
9,1
|
|
45
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
4
|
|
46
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
2,3
|
|
47
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0,8
|
Pour estimer le temps total passé à
l'hôpital par les femmes d'un certain âge nous
générons le tableau croisé des durées
d'hospitalisation en fonction de l'âge. Ce tableau nous permettra de
calculer l'exposition au risque dans l'état hospitalisé.
Tableau.12. Exposition au risque dans l'état
«hospitalisé ».
|
Tableau croisé Age * Durée
|
|
Durée
|
|
|
Age
|
1
|
2
|
3
|
|
|
15
|
8
|
0
|
0
|
8
|
|
16
|
7
|
1
|
0
|
9
|
|
17
|
15
|
3
|
0
|
21
|
|
18
|
7
|
3
|
0
|
13
|
|
19
|
15
|
1
|
0
|
17
|
|
20
|
12
|
2
|
0
|
16
|
|
21
|
10
|
1
|
0
|
12
|
|
22
|
14
|
2
|
0
|
18
|
|
23
|
7
|
1
|
0
|
9
|
|
24
|
5
|
2
|
1
|
12
|
|
25
|
15
|
0
|
0
|
15
|
|
26
|
9
|
2
|
0
|
13
|
|
27
|
17
|
2
|
0
|
21
|
|
28
|
10
|
0
|
0
|
10
|
|
29
|
7
|
1
|
0
|
9
|
|
30
|
10
|
1
|
1
|
15
|
|
31
|
6
|
4
|
1
|
17
|
|
32
|
7
|
0
|
0
|
7
|
|
33
|
12
|
1
|
0
|
14
|
|
34
|
8
|
1
|
0
|
10
|
|
35
|
13
|
3
|
0
|
19
|
|
36
|
6
|
0
|
0
|
6
|
|
37
|
16
|
3
|
1
|
25
|
|
38
|
6
|
1
|
0
|
8
|
|
39
|
11
|
1
|
0
|
13
|
|
40
|
8
|
0
|
0
|
8
|
|
41
|
5
|
0
|
0
|
5
|
|
42
|
5
|
1
|
0
|
7
|
|
43
|
4
|
0
|
0
|
4
|
|
44
|
4
|
1
|
0
|
6
|
|
45
|
1
|
0
|
0
|
1
|
|
46
|
2
|
0
|
0
|
2
|
|
47
|
1
|
0
|
0
|
1
|
Tableau.13. Exposition au risque dans l'état
« actif ».
|
Tableau croisé Age * Activité
|
|
Activité
|
|
|
Age
|
350,0
|
355,0
|
356,0
|
357,0
|
358,0
|
359,0
|
359,1
|
359,2
|
359,5
|
359,7
|
|
|
15
|
0
|
3
|
2
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
2833,5
|
|
16
|
0
|
1
|
1
|
0
|
0
|
4
|
0
|
0
|
2
|
0
|
2826
|
|
17
|
0
|
5
|
3
|
1
|
0
|
4
|
0
|
0
|
4
|
1
|
6353,7
|
|
18
|
0
|
2
|
2
|
0
|
1
|
3
|
0
|
0
|
2
|
0
|
3536
|
|
19
|
0
|
3
|
5
|
0
|
1
|
3
|
0
|
0
|
3
|
1
|
5658,2
|
|
20
|
0
|
2
|
5
|
0
|
0
|
5
|
0
|
0
|
1
|
1
|
4984,2
|
|
21
|
0
|
2
|
0
|
1
|
0
|
4
|
0
|
0
|
3
|
1
|
3881,2
|
|
22
|
0
|
3
|
2
|
1
|
0
|
6
|
0
|
0
|
4
|
0
|
5646
|
|
23
|
0
|
1
|
3
|
0
|
0
|
1
|
0
|
0
|
3
|
0
|
2800,5
|
|
24
|
0
|
3
|
0
|
1
|
0
|
4
|
0
|
0
|
0
|
0
|
2858
|
|
25
|
0
|
3
|
4
|
0
|
0
|
1
|
0
|
0
|
6
|
1
|
5244,7
|
|
26
|
0
|
1
|
1
|
0
|
0
|
6
|
0
|
0
|
2
|
1
|
3903,7
|
|
27
|
0
|
2
|
3
|
0
|
0
|
5
|
0
|
0
|
9
|
0
|
6628,5
|
|
28
|
0
|
5
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
3546,2
|
|
29
|
0
|
0
|
3
|
1
|
0
|
3
|
0
|
0
|
1
|
0
|
2841,5
|
|
30
|
0
|
1
|
4
|
1
|
0
|
4
|
0
|
0
|
1
|
1
|
4271,2
|
|
31
|
0
|
3
|
0
|
1
|
0
|
5
|
0
|
0
|
1
|
1
|
3916,2
|
|
32
|
0
|
1
|
0
|
1
|
0
|
2
|
0
|
0
|
1
|
2
|
2488,9
|
|
33
|
0
|
2
|
2
|
0
|
0
|
2
|
0
|
0
|
5
|
2
|
4556,9
|
|
34
|
0
|
2
|
1
|
1
|
0
|
1
|
0
|
0
|
4
|
0
|
3140
|
|
35
|
0
|
1
|
4
|
0
|
0
|
7
|
0
|
0
|
3
|
1
|
5670,2
|
|
36
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
4
|
0
|
2073
|
|
37
|
1
|
6
|
4
|
0
|
0
|
5
|
1
|
0
|
1
|
2
|
7117
|
|
38
|
0
|
4
|
0
|
0
|
0
|
1
|
0
|
0
|
2
|
0
|
2458
|
|
39
|
0
|
0
|
6
|
0
|
0
|
6
|
0
|
0
|
0
|
0
|
4290
|
|
40
|
0
|
1
|
5
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
2831,5
|
|
41
|
0
|
0
|
2
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1788,7
|
|
42
|
0
|
1
|
1
|
0
|
0
|
2
|
0
|
0
|
1
|
1
|
2128,2
|
|
43
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1429,7
|
|
44
|
0
|
0
|
2
|
0
|
0
|
1
|
0
|
0
|
0
|
2
|
1790,4
|
|
45
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
356
|
|
46
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
717,7
|
|
47
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
359,2
|
Tableau.14. Nombre de transition de l'état
«hospitalisé» à l'état
« actif »
|
Tableau croisé Age * Ttransition_ha
|
|
Ttransition_ha
|
|
|
Age
|
0,3
|
0,5
|
0,7
|
0,8
|
1
|
|
|
15
|
0
|
2
|
0
|
0
|
6
|
7
|
|
16
|
0
|
4
|
0
|
0
|
4
|
6
|
|
17
|
1
|
7
|
0
|
0
|
10
|
13,8
|
|
18
|
0
|
5
|
0
|
0
|
5
|
7,5
|
|
19
|
1
|
4
|
0
|
0
|
11
|
13,3
|
|
20
|
0
|
4
|
0
|
0
|
10
|
12
|
|
21
|
1
|
4
|
0
|
0
|
6
|
8,3
|
|
22
|
1
|
4
|
0
|
0
|
11
|
13,3
|
|
23
|
0
|
3
|
0
|
0
|
5
|
6,5
|
|
24
|
0
|
3
|
0
|
0
|
5
|
6,5
|
|
25
|
2
|
6
|
0
|
0
|
7
|
10,6
|
|
26
|
2
|
4
|
0
|
0
|
5
|
7,6
|
|
27
|
1
|
9
|
0
|
0
|
9
|
13,8
|
|
28
|
1
|
2
|
0
|
0
|
7
|
8,3
|
|
29
|
0
|
2
|
0
|
1
|
5
|
6,8
|
|
30
|
1
|
2
|
0
|
0
|
9
|
10,3
|
|
31
|
1
|
4
|
0
|
0
|
6
|
8,3
|
|
32
|
2
|
1
|
0
|
0
|
4
|
5,1
|
|
33
|
2
|
6
|
0
|
0
|
5
|
8,6
|
|
34
|
0
|
5
|
0
|
0
|
4
|
6,5
|
|
35
|
0
|
5
|
0
|
0
|
11
|
13,5
|
|
36
|
0
|
3
|
0
|
0
|
3
|
4,5
|
|
37
|
4
|
5
|
1
|
0
|
10
|
14,4
|
|
38
|
0
|
4
|
0
|
0
|
3
|
5
|
|
39
|
0
|
0
|
0
|
0
|
12
|
12
|
|
40
|
0
|
1
|
0
|
0
|
7
|
7,5
|
|
41
|
1
|
0
|
0
|
0
|
4
|
4,3
|
|
42
|
1
|
2
|
0
|
0
|
3
|
4,3
|
|
43
|
1
|
1
|
0
|
0
|
2
|
2,8
|
|
44
|
1
|
2
|
0
|
0
|
2
|
3,3
|
|
45
|
1
|
0
|
0
|
0
|
0
|
0,3
|
|
46
|
1
|
0
|
0
|
0
|
1
|
1,3
|
|
47
|
0
|
0
|
0
|
0
|
1
|
1
|
Nous pouvons maintenant estimer le taux de transition de
l'état « hospitalisé » à l'état
« actif »
Tableau.15. Estimation des taux de transition  de l'état « actif » à l'état
« hospitalisé ». de l'état « actif » à l'état
« hospitalisé ».
|
Age
|
|
|
|
|
15
|
2833,5
|
26,5
|
0,00935239
|
|
16
|
2826
|
13,5
|
0,00477707
|
|
17
|
6353,7
|
44,8
|
0,00705101
|
|
18
|
3536
|
22
|
0,00622172
|
|
19
|
5658,2
|
41,3
|
0,00729914
|
|
20
|
4984,2
|
34,8
|
0,00698206
|
|
21
|
3881,2
|
18,3
|
0,00471504
|
|
22
|
5646
|
33
|
0,00584485
|
|
23
|
2800,5
|
19
|
0,0067845
|
|
24
|
2858
|
19
|
0,00664801
|
|
25
|
5244,7
|
35,3
|
0,0067306
|
|
26
|
3903,7
|
15,3
|
0,00391936
|
|
27
|
6628,5
|
30,5
|
0,00460134
|
|
28
|
3546,2
|
33,8
|
0,00953133
|
|
29
|
2841,5
|
18
|
0,00633468
|
|
30
|
4271,2
|
26,3
|
0,00615752
|
|
31
|
3916,2
|
19,8
|
0,00505592
|
|
32
|
2488,9
|
11,1
|
0,0044598
|
|
33
|
4556,9
|
22,6
|
0,00495951
|
|
34
|
3140
|
19,5
|
0,00621019
|
|
35
|
5670,2
|
28,3
|
0,00499101
|
|
36
|
2073
|
7
|
0,00337675
|
|
37
|
7117
|
56,4
|
0,00792469
|
|
38
|
2458
|
21,5
|
0,00874695
|
|
39
|
4290
|
29,5
|
0,00687646
|
|
40
|
2831,5
|
28,5
|
0,01006534
|
|
41
|
1788,7
|
11,3
|
0,00631744
|
|
42
|
2128,2
|
11,3
|
0,00530965
|
|
43
|
1429,7
|
10,3
|
0,00720431
|
|
44
|
1790,4
|
9,1
|
0,00508266
|
|
45
|
356
|
4
|
0,01123596
|
|
46
|
717,7
|
2,3
|
0,00320468
|
|
47
|
359,2
|
0,8
|
0,00222717
|

Graph3. Représentation graphique des taux de
transition ah en fonction de l'âge.
Nous pouvons maintenant estimer le taux de transition de
l'état « hospitalisé » à l'état
« actif»
Tableau.16. Estimation des taux de transition  de l'état « hospitalisé » à
l'état « actif ». de l'état « hospitalisé » à
l'état « actif ».
|
Age
|
|
|
|
|
15
|
7
|
8
|
0,875
|
|
16
|
6
|
9
|
0,66666667
|
|
17
|
13,8
|
21
|
0,65714286
|
|
18
|
7,5
|
13
|
0,57692308
|
|
19
|
13,3
|
17
|
0,78235294
|
|
20
|
12
|
16
|
0,75
|
|
21
|
8,3
|
12
|
0,69166667
|
|
22
|
13,3
|
18
|
0,73888889
|
|
23
|
6,5
|
9
|
0,72222222
|
|
24
|
6,5
|
12
|
0,54166667
|
|
25
|
10,6
|
15
|
0,70666667
|
|
26
|
7,6
|
13
|
0,58461538
|
|
27
|
13,8
|
21
|
0,65714286
|
|
28
|
8,3
|
10
|
0,83
|
|
29
|
6,8
|
9
|
0,75555556
|
|
30
|
10,3
|
15
|
0,68666667
|
|
31
|
8,3
|
17
|
0,48823529
|
|
32
|
5,1
|
7
|
0,72857143
|
|
33
|
8,6
|
14
|
0,61428571
|
|
34
|
6,5
|
10
|
0,65
|
|
35
|
13,5
|
19
|
0,71052632
|
|
36
|
4,5
|
6
|
0,75
|
|
37
|
14,4
|
25
|
0,576
|
|
38
|
5
|
8
|
0,625
|
|
39
|
12
|
13
|
0,92307692
|
|
40
|
7,5
|
8
|
0,9375
|
|
41
|
4,3
|
5
|
0,86
|
|
42
|
4,3
|
7
|
0,61428571
|
|
43
|
2,8
|
4
|
0,7
|
|
44
|
3,3
|
6
|
0,55
|
|
45
|
0,3
|
1
|
0,3
|
|
46
|
1,3
|
2
|
0,65
|
|
47
|
1
|
1
|
1
|

Graph4. Représentation graphique des taux de
transition ha en fonction de l'âge.
Tableau.17. Taux de transition pour les services
maternité et Gynécologie
|
Age
|
|
|
|
|
|
15
|
0,00935239
|
0,875
|
0,0013947
|
0,16666667
|
|
16
|
0,00477707
|
0,66666667
|
0,0013947
|
0,16666667
|
|
17
|
0,00705101
|
0,65714286
|
0,0013947
|
0,16666667
|
|
18
|
0,00622172
|
0,57692308
|
0,0013947
|
0,16666667
|
|
19
|
0,00729914
|
0,78235294
|
0,0013947
|
0,16666667
|
|
20
|
0,00698206
|
0,75
|
0,0013947
|
0,16666667
|
|
21
|
0,00471504
|
0,69166667
|
0,0013947
|
0,16666667
|
|
22
|
0,00584485
|
0,73888889
|
0,0013947
|
0,16666667
|
|
23
|
0,0067845
|
0,72222222
|
0,0013947
|
0,16666667
|
|
24
|
0,00664801
|
0,54166667
|
0,0013947
|
0,16666667
|
|
25
|
0,0067306
|
0,70666667
|
0,0013947
|
0,16666667
|
|
26
|
0,00391936
|
0,58461538
|
0,0013947
|
0,16666667
|
|
27
|
0,00460134
|
0,65714286
|
0,0013947
|
0,16666667
|
|
28
|
0,00953133
|
0,83
|
0,0013947
|
0,16666667
|
|
29
|
0,00633468
|
0,75555556
|
0,00102164
|
0,1
|
|
30
|
0,00615752
|
0,68666667
|
0,00083542
|
0,1
|
|
31
|
0,00505592
|
0,48823529
|
0,00102746
|
0,1
|
|
32
|
0,0044598
|
0,72857143
|
0,0009152
|
0,1
|
|
33
|
0,00495951
|
0,61428571
|
0,00083542
|
0,1
|
|
34
|
0,00621019
|
0,65
|
0,00094014
|
0,08333333
|
|
35
|
0,00499101
|
0,71052632
|
0,00081797
|
0,08333333
|
|
36
|
0,00337675
|
0,75
|
0,00073077
|
0,08333333
|
|
37
|
0,00792469
|
0,576
|
0,00069589
|
0,08333333
|
|
38
|
0,00874695
|
0,625
|
0,00087032
|
0,08333333
|
|
39
|
0,00687646
|
0,92307692
|
0,00069589
|
0,08333333
|
|
40
|
0,01006534
|
0,9375
|
0,00069589
|
0,08333333
|
|
41
|
0,00631744
|
0,86
|
0,00069589
|
0,08333333
|
|
42
|
0,00530965
|
0,61428571
|
0
|
0
|
|
43
|
0,00720431
|
0,7
|
0
|
0
|
|
44
|
0,00508266
|
0,55
|
0
|
0
|
|
45
|
0,01123596
|
0,3
|
0
|
0
|
|
46
|
0,00320468
|
0,65
|
0
|
0
|
|
47
|
0,00222717
|
1
|
0
|
0
|
3.12. Estimation des probabilités
de transition
Dans cette partie nous allons montrer comment on peut obtenir
les probabilités de transition à partir des taux qui viennent
d'être obtenus. Sur la figure Graph1 représentant  en fonction du temps. On remarque que le taux est constant de 15
à 28 ans puis décroit de 28 à 30 ans environs pour se
stabiliser ensuite à 39 ans. en fonction du temps. On remarque que le taux est constant de 15
à 28 ans puis décroit de 28 à 30 ans environs pour se
stabiliser ensuite à 39 ans.
De même sur la figure représentant le taux de
transition  en fonction de l'âge, on remarque un premier pic important entre
28 et 30 ans. Il sera alors plus intéressant de traiter en
général ce cas particulier car pour les autres cas les taux sont
presque identiques. en fonction de l'âge, on remarque un premier pic important entre
28 et 30 ans. Il sera alors plus intéressant de traiter en
général ce cas particulier car pour les autres cas les taux sont
presque identiques.
Prenons le taux de transition correspondant à 28, 29 et
30 ans et représentons leur matrice des taux de transition.
 , Idem pour M29, M30. , Idem pour M29, M30.



Trouvons maintenant les valeurs et les vecteurs propres
associées aux matrices . .
Pour la matrice  ; ;

Pour la matrice  ; ;

Pour la matrice  ; ;

Les matrices des probabilités annuelles de transition
à l'instant t (année de la souscription du contrât) sont
donnée par :
 = =
 = =
En procédant de la même façon nous obtenons


Calculons maintenant les probabilités de transition sur
les 3 années,

Le calcul des probabilités de transition sur 3
années nous permet d'extraire la valeur  qui est la probabilité pour qu'une assurée active
à l'âge de 28 ans, le soit également à l'âge
de 29 et 30 ans. Cette valeur va nous permettre de calculer la prime annuelle
que l'assuré doit verser. qui est la probabilité pour qu'une assurée active
à l'âge de 28 ans, le soit également à l'âge
de 29 et 30 ans. Cette valeur va nous permettre de calculer la prime annuelle
que l'assuré doit verser.
3.13. Estimation de la prime (28-30
ans)
En se référant à la formule du calcul de
la prime sur base de l'équivalence, on estime la prime unique pure par
la formule
 avec n le nombre d'année pour lequel l'assuré a souscrit
un contrat ;on multipliera chaque membre de cette formule par les
délais de carences concernées. En pratique le délai de
carence est de 4 mois dans le cas d'une hospitalisation simple et de 9 mois
dans le cas d'une hospitalisation pour un accouchement. avec n le nombre d'année pour lequel l'assuré a souscrit
un contrat ;on multipliera chaque membre de cette formule par les
délais de carences concernées. En pratique le délai de
carence est de 4 mois dans le cas d'une hospitalisation simple et de 9 mois
dans le cas d'une hospitalisation pour un accouchement.
Pour une femme de 28 ans qui vient s'assurer pour 3 ans, la prime
annuelle sera de

Avec  : la variation de délais de carence en fonction du temps
pour les hospitalisations ; : la variation de délais de carence en fonction du temps
pour les hospitalisations ;
 : la variation de délais de carence en fonction du temps
pour les accouchement s. : la variation de délais de carence en fonction du temps
pour les accouchement s.
Les  sont de montant de dépense actualisé à un taux de
4%. C'est souvent le taux d'intérêt de la Banque National qui est
utilisé. sont de montant de dépense actualisé à un taux de
4%. C'est souvent le taux d'intérêt de la Banque National qui est
utilisé.
Suite aux nombreux membres que possède cette formule
ilest plus facile d'effectuerle calcul à l'aide d'un tableur comme
ci-dessous :
Calculons la prime pour les hospitalisations
|
t
|
|
|
v(x)
|
v(x) actu
|
|

|

|

|
|
0
|
0,9922763
|
0,0095313
|
43350
|
43350
|
0,4383613
|
19002,962
|
|
|
|
1
|
0,9945998
|
0,0063347
|
37887,5
|
39344,71154
|
0,4712161
|
18539,861
|
18539,86
|
|
|
2
|
0,9947670
|
0,0061575
|
41058,33
|
44155,92945
|
0,5046035
|
22281,236
|
22281,236
|
22281,236
|
|
|
|
|
|
|

|
1914369,9336
|
1265454,040
|
668437,096
|
|
|
|
|
|
|
|
18105,561
|
7972,957
|
4094,376
|
 (h)=18105,561+7972,957+4094,376=30172,89 FC (h)=18105,561+7972,957+4094,376=30172,89 FC
 (h)=30172,89, c'est-à-dire que cette assurée va payer une
prime annuelle de 30172,89 FC pour s'assurer pendant 3 ans contre un sinistre
quelconque (n'importe quelles maladies de notre échantillon). Cette
assurée paiera 90518FC pour assurer ces soins pendant 3 ans au lieu de
payer 122295FC s'elle n'avait pas souscrit une assurance.Voir tableau18 en
Annexe. (h)=30172,89, c'est-à-dire que cette assurée va payer une
prime annuelle de 30172,89 FC pour s'assurer pendant 3 ans contre un sinistre
quelconque (n'importe quelles maladies de notre échantillon). Cette
assurée paiera 90518FC pour assurer ces soins pendant 3 ans au lieu de
payer 122295FC s'elle n'avait pas souscrit une assurance.Voir tableau18 en
Annexe.
Calculons la prime pour les accouchements
|
t
|
|
|
v(x)
|
V(x) actu
|
|
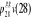
|

|

|
|
0
|
0,9922763
|
0,00139470
|
213800
|
213800
|
0,8468550
|
181057,59
|
|
|
|
1
|
0,9945998
|
0,00102164
|
213800
|
222023,079
|
0,9048851
|
200905,374
|
193464,430
|
|
|
2
|
0,9947670
|
0,00083542
|
213800
|
229929,87
|
0,9048764
|
208058,12
|
193462,570
|
193462,57
|
|
|
|
|
|
|

|
18880675,095
|
11994737,260
|
5803877,22
|
|
|
|
|
|
|
|
26129,490
|
12188,12
|
4823,30
|
 (g)= 43140,92FC, c'est-à-dire que cette assurée va payer
une prime annuelle de 43140,92FC pour assurer sont accouchement dans 3 ans.Cela
fait un total de 129420FC pour assurer son accouchement pendant 3 ans maximum
au lieu de payer 213800FC s'elle n'avait pas souscrite une assurance.Voir
tableau18 en Annexe. (g)= 43140,92FC, c'est-à-dire que cette assurée va payer
une prime annuelle de 43140,92FC pour assurer sont accouchement dans 3 ans.Cela
fait un total de 129420FC pour assurer son accouchement pendant 3 ans maximum
au lieu de payer 213800FC s'elle n'avait pas souscrite une assurance.Voir
tableau18 en Annexe.
On peut également calculer la prime pour les
assurées de 25 ans à 27 ans. En se référant
à Graph1, ce montant sera égal pour toutes les assurées
dont l'âge varie entre 15 et 27 ans. En se référant au
Graph 3. Il ya une pente importante avant une reprise qui monte en pic de taux
de transition. Nous allons donc calculer la prime pour cet intervalle.
3.14. Estimation de la prime de risques
pour les assurées de 25 à 27 ans
 = =
 = =
 = =
Calculons la prime pour les hospitalisations
|
t
|
|
|
v(x)
|
v(x) actu
|
|

|

|

|
|
0
|
0,9946144
|
0,00673060
|
38640
|
38640
|
0,4383613
|
32717,129
|
|
|
|
1
|
0,9957579
|
0,00391936
|
36790,909
|
38205,944
|
0,4712161
|
21322,825
|
20533,090
|
|
|
2
|
0,9953553
|
0,00460134
|
36436,842
|
39185,775
|
0,5046035
|
20349,796
|
18922,231
|
18922,23
|
|
|
|
|
|
|

|
2380472,029
|
1223114,995
|
567666,943
|
|
|
|
|
|
|
|
15935,7169
|
4773,4920
|
2599,896
|
 (h)=15935,7169+4773,4920+2599,896=23309,10 FC (h)=15935,7169+4773,4920+2599,896=23309,10 FC
 (h)= 23309,10 FC, c'est-à-dire que cette assurée va payer
une prime annuelle de 23309,10 FC pour s'assurer pendant 3 ans contre un
sinistre quelconque (n'importe quelles maladies de notre échantillon).
Cela fait un total de 69927,3FC pour assurer ces soins pendant 3 ans au lieu
de payer 111867,751 si elle n'avait pas souscrite une assurance.Voir tableau18
en Annexe pour les dépenses de santé. (h)= 23309,10 FC, c'est-à-dire que cette assurée va payer
une prime annuelle de 23309,10 FC pour s'assurer pendant 3 ans contre un
sinistre quelconque (n'importe quelles maladies de notre échantillon).
Cela fait un total de 69927,3FC pour assurer ces soins pendant 3 ans au lieu
de payer 111867,751 si elle n'avait pas souscrite une assurance.Voir tableau18
en Annexe pour les dépenses de santé.
Calculons la prime pour les accouchements
|
t
|
|
|
v(x)
|
V(x) actu
|
|

|
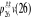
|

|
|
0
|
0,9946144
|
0,00139470
|
213800
|
213800
|
0,5199258
|
111160,136
|
|
|
|
1
|
0,9957579
|
0,00139470
|
213800
|
222023,0769
|
0,8465856
|
187961,53
|
181000,001
|
|
|
2
|
0,9953553
|
0,00139470
|
213800
|
229929,8817
|
0,8465856
|
194655,32
|
181000,001
|
181000,00
|
|
|
|
|
|
|

|
15800864,084
|
11222000,079
|
5430000,03
|
|
|
|
|
|
|
|
21918,780
|
15584,929
|
7538,045
|
 (g)= 21918,780+15584,929+7538,045=45041,75 FC (g)= 21918,780+15584,929+7538,045=45041,75 FC
C'est-à-dire cette assurée va payer une prime
annuelle de 45041,75 FC pour assurer sont accouchement dans 3 ans. Ce qui fera
un total de 135125,25 FC pour assurer sont accouchement pendant 3 ans maximum
au lieu de payer 213800FC s'elle n'avait pas souscrit une assurance.Voir
tableau18 en Annexe.
Conclusion
En guise de conclusion, dans ce travail nous avons
montré l'intérêt des processus stochastique pour
modéliser un contrat d'assurance maladie. En effet, un assuré
évolue dans différents états et les transitions entre les
états et/ou les durées de séjour déterminent les
montants des primes. Les recours à un processus ponctuel , ou pour tout instant t, xt donne l'état ou se
trouve l'individu à ce moment. Pour modéliser l'histoire de cet
assuré ce processus est donc tout à fait approprié. , ou pour tout instant t, xt donne l'état ou se
trouve l'individu à ce moment. Pour modéliser l'histoire de cet
assuré ce processus est donc tout à fait approprié.
Cette modélisation dynamique envisageant le produit
d'assurance dans toute sa durée s'impose notamment aussi lorsque les
primes sont nivelées dans le temps. Le montant dépend alors de
l'âge de l'assuré à la souscription de la police et
n'évolue plus ensuite pendant une durée quelconque même si
les probabilités de versement de prestations sont amenés à
croitre. Il s'ensuit que l'assureur doit provisionner une partie des primes au
début du contrat pour faire face aux charges futures. Ce sont ces
aspects qui nous ont poussés à utiliser le processus ponctuel.
Comme vous le remarquerez, nous n'avons pas regroupé
les valeurs observées dans notre échantillon mais le groupement
se fait par observations des courbes des taux des transitions en fonction
des âges; on peut comprendre que l'approche analytique à lui seul
ne permet pas de calculer la prime il faut également une observation
graphique des tendances.
Nous avons eu des difficultés au cours des ces
analyses, dont l'une est d'estimer la prime annuelle à partir de
l'approche continu de la fonction de calcul des primes, nous avons
utilisé une approche discrète qui a cependant des
inconvénients car certains paramètre ne sont pas pris en compte.
En effet l'approche continue demande d'étudier la distribution de
probabilité des dépenses des ménages pour les soins de
santé et l'ajuster à une distribution continue connue (Loi
normale, loi de Student) afin de déduire sa fonction de
répartition. Fautes des temps et des ressources nous n'avons pas su
aborder cette approche qui donne des meilleurs estimations. Nous laissons donc
ouvert la continuité de ces travaux pour nos recherches futures.
Notre travail a apporté une modeste contribution dans
l'étude des modèles d'assurance et nous ne prétendons en
aucun cas avoir abordé tous les points essentiels fautes des moyens et
des temps, nous espérons que d'autres personnes pourront contribuer
à la consolidation de cet oeuvre en élargissant notre
étude et en apportant des correctifs à des erreurs
rencontrés.
Annexe A
Tableau.1. Tableau croisée des transitions en
fonction des âges
|
|
Transition
|
Total
|
|
Age
|
0,25
|
0,3
|
0,5
|
|
|
15
|
0
|
0
|
1
|
1
|
|
16
|
0
|
0
|
2
|
2
|
|
17
|
0
|
0
|
1
|
1
|
|
18
|
0
|
0
|
2
|
2
|
|
19
|
0
|
0
|
4
|
4
|
|
20
|
0
|
0
|
5
|
5
|
|
21
|
0
|
0
|
8
|
8
|
|
22
|
0
|
0
|
6
|
6
|
|
23
|
0
|
0
|
11
|
11
|
|
24
|
0
|
0
|
3
|
3
|
|
25
|
0
|
0
|
6
|
6
|
|
26
|
0
|
0
|
11
|
11
|
|
27
|
0
|
0
|
6
|
6
|
|
28
|
0
|
0
|
8
|
8
|
|
29
|
0
|
2
|
1
|
3
|
|
30
|
0
|
7
|
0
|
7
|
|
31
|
1
|
4
|
3
|
8
|
|
32
|
0
|
6
|
1
|
7
|
|
33
|
0
|
10
|
0
|
10
|
|
34
|
1
|
2
|
1
|
4
|
|
35
|
5
|
2
|
1
|
8
|
|
36
|
3
|
1
|
0
|
4
|
|
37
|
6
|
0
|
0
|
6
|
|
38
|
3
|
0
|
1
|
4
|
|
39
|
1
|
0
|
0
|
1
|
|
40
|
3
|
0
|
0
|
3
|
|
42
|
1
|
0
|
0
|
1
|
Tableau.2. Tableau croisée des durées
d'hospitalisation en fonction des âges
|
Durée
|
Total
|
|
Age
|
3
|
|
|
15
|
1
|
3
|
|
16
|
2
|
6
|
|
17
|
1
|
3
|
|
18
|
2
|
6
|
|
19
|
4
|
12
|
|
20
|
5
|
15
|
|
21
|
8
|
24
|
|
22
|
6
|
18
|
|
23
|
11
|
33
|
|
24
|
3
|
9
|
|
25
|
6
|
18
|
|
26
|
11
|
33
|
|
27
|
6
|
18
|
|
28
|
8
|
24
|
|
29
|
3
|
9
|
|
30
|
7
|
21
|
|
31
|
8
|
24
|
|
32
|
7
|
21
|
|
33
|
10
|
30
|
|
34
|
4
|
12
|
|
35
|
8
|
24
|
|
36
|
4
|
12
|
|
37
|
6
|
18
|
|
38
|
4
|
12
|
|
39
|
1
|
3
|
|
40
|
3
|
9
|
|
42
|
1
|
3
|
Tableau.3. Frais moyen des prises en charge pour la
gynéco-obstétrique et maternité
|
Age
|
Frais moyen
gynéco
|
Frais moyen
maternité
|
|
15
|
27562,5
|
213800
|
|
16
|
29762,5
|
213800
|
|
17
|
37461,1111
|
213800
|
|
18
|
32970
|
213800
|
|
19
|
36243,75
|
213800
|
|
20
|
36085,7143
|
213800
|
|
21
|
33763,6364
|
213800
|
|
22
|
35987,5
|
213800
|
|
23
|
28750
|
213800
|
|
24
|
38975
|
213800
|
|
25
|
38640
|
213800
|
|
26
|
36790,9091
|
213800
|
|
27
|
36436,8421
|
213800
|
|
28
|
43350
|
213800
|
|
29
|
37887,5
|
213800
|
|
30
|
41058,3333
|
213800
|
|
31
|
37636,3636
|
213800
|
|
32
|
48785,7143
|
213800
|
|
33
|
40261,5385
|
213800
|
|
34
|
34366,6667
|
213800
|
|
35
|
37556,25
|
213800
|
|
36
|
29933,3333
|
213800
|
|
37
|
45375
|
213800
|
|
38
|
45514,2857
|
213800
|
|
39
|
33341,6667
|
213800
|
|
40
|
36537,5
|
213800
|
|
41
|
48340
|
213800
|
|
42
|
47583,3333
|
213800
|
|
43
|
59275
|
213800
|
|
44
|
54100
|
213800
|
|
45
|
53100
|
213800
|
|
46
|
69500
|
213800
|
Tableau.17. Pathologie et complications
considérées dans le cadre de notre étude
|
nombre
|
Complication et pathologie traité dans notre
étude
|
|
1
|
Anémie
|
|
5
|
Cardiopathie
|
|
6
|
Diabète
|
|
7
|
Dysgravidie
|
|
10
|
Gastroentérite
|
|
8
|
IST (Infection Sexuellement transmissible)
|
|
2
|
lombohypogastralgie
|
|
3
|
MAP (Menace d'avortement précoce)
|
|
9
|
MAS (Menace d'avortement Sévère)
|
|
4
|
Paludisme
|
Annexe B
Rappels de statistique
B.1.
ExpérienceAléatoire
Une expérienceAléatoire î est une
expérience dont on ne peut pas prédire avec certitude les
résultats du faits qu'on ne contrôle pas toutes les causes qui
peuvent influencés ces résultats ; mais dont on
connaît à priori tous les résultats possible auxquels elle
donnera lieu.
B.2. Eventualité
Soit î une expériencealéatoire, alors par
définition une éventualité est un résultat possible
à priori de î. L'ensemble de toutes les éventualités
relatives à î, noté par Ù s'appelle
« l'espace des éventualités ».
B.3.
ó-Algèbre
Soit Ù l'espace des éventualités relatif
à une expériencealéatoire î, la tribu ou la
ó-Algèbre notée á, est l'ensemble á non
vide et jouissant des propriétés suivantes :
1. Ù  á, á,
2. si A  á, alors á, alors   Ac Ac á, A étant un événement qui lors d'une
expériencealéatoire, peut ou peut ne pas se réaliser. á, A étant un événement qui lors d'une
expériencealéatoire, peut ou peut ne pas se réaliser.
3. Si A1,A2,A3, ...Ai... est une suite
d'élément dans á alors, toute suite   á est stable par rapport à l'union dénombrable á est stable par rapport à l'union dénombrable
B.4. Probabilité
(Définition axiomatique)
Considérons la plus grande tribu á sur l'espace
d'éventualité Ù, on appelle probabilité,
l'application numérique IP : á?IR et qui vérifie les
axiomes suivantes,
Ax1) A  á, alors IP(A)=0, á, alors IP(A)=0,
Ax2) si A1,A2,...,Ai une suite quelconque
d'événement de á tel que AjnAk= pour j?k, alors IP( pour j?k, alors IP( )= )=  (Axiome de la ó-additivité) (Axiome de la ó-additivité)
Ax3. IP(Ù)=1
B.5. Variables
aléatoires
- les boréliens : on appelle tribu boréliennes
B sur IR la ó-Algèbre engendré par tous les intervalles de
IR. Les éléments de la tribu borélienne B sur IR sont des
Borélien.
- On appelle variable aléatoire, l'application X :
(Ù,á)?(IR,B) tel que â B : X-1(â) B : X-1(â)  á á
B.6. Processus
stochastiques
a) Définition : On appelle processus stochastique (ou
aléatoire) une famille de variable aléatoire noté
Xt X(t), t X(t), t  T T  IR+, définie sur un espace probabilisé
(Ù,á,IP) et dépendantes du temps t IR+, définie sur un espace probabilisé
(Ù,á,IP) et dépendantes du temps t  T T IR+ ; ou T IR+ ; ou T IR+ s'appelle espace des instants. Xt IR+ s'appelle espace des instants. Xt X(t) est une réalisation du processus aléatoire {X(t), t X(t) est une réalisation du processus aléatoire {X(t), t
 T T IR+ } à l'instant t . IE= IR+ } à l'instant t . IE= ( Ù) : l'ensemble de toutes les réalisations du
processus stochastique. ( Ù) : l'ensemble de toutes les réalisations du
processus stochastique.
{X(t), t T T IR+} espace des états du processus stochastique
considéré. IR+} espace des états du processus stochastique
considéré.
b) Classification de processus stochastique
La classification de processus stochastique se base sur la
cardinalité de T et de E.
1) Si T est isomorphe à R T R+ et E R+ et E R+ , alors {X(t), t R+ , alors {X(t), t T} est dit processus stochastique continu dans le temps et dans l'espace
des instants. T} est dit processus stochastique continu dans le temps et dans l'espace
des instants.
2) Si T est isomorphe à R T R+ et E R+ et E J J IN, alors {X(t), t IN, alors {X(t), t T} est dit processus stochastique continu dans le temps et discontinu
dans l'espace des instants. T} est dit processus stochastique continu dans le temps et discontinu
dans l'espace des instants.
3) Si T est isomorphe à R T I I IN et E IN et E J J IN, alors {X(t), t IN, alors {X(t), t T} est dit processus stochastique discontinu dans le temps et discontinu
dans l'espace des instants. T} est dit processus stochastique discontinu dans le temps et discontinu
dans l'espace des instants.
B.7. Fonction de
renouvellement simple
Considérons une suite des variables aléatoires
discrètes Ti (i IN), stochastiquementindépendant et equidistribué sur un
même espace probabilisé (Ù,á,IP) tel que leur
fonction de répartition commune F(t)=IP(T=t) est donnée avec
F(t)=0, IN), stochastiquementindépendant et equidistribué sur un
même espace probabilisé (Ù,á,IP) tel que leur
fonction de répartition commune F(t)=IP(T=t) est donnée avec
F(t)=0,  t=0. t=0.
On constate que {Ti, i IN} est un processus continu dans le temps et discontinue dans l'espace
des états. IN} est un processus continu dans le temps et discontinue dans l'espace
des états.
Interevenement : intervalle de temps qui sépare 2
événementconsécutifs ;
Renouvellement simple : lorsque les événements
Ev1,Ev2,..., Evn ont la même caractéristique.
Dès lors ; Sn= : la date du nième renouvellement simple. : la date du nième renouvellement simple.
N(x) est le nombre de renouvellement simple (PRS), la famille {
Sn= ,n ,n IN} IN} {N(x), x=0} {N(x), x=0}
La fonction de renouvellement simple U(x) est dons le nombre
moyen de renouvellement simple dans l'intervalle de temps 

B.8. Distribution de
probabilité de la variable aléatoire x
Déf : Soit x une variable aléatoire
défini sur (Ù,á,IP), on appelle distribution de
probabilité de la variable aléatoire x, l'application
 tq tq  â â B, B,  (â)= (â)=  [ [ (â)]= (â)]=  [{ù [{ù Ù /X(ù) Ù /X(ù)  â}] â}]
1) Distribution de probabilité d'une variable
aléatoire discrète
Lorsque x= V.A.D (variable aléatoire discrète), on
a  ={ ={ tq tq  } }
2) Distribution de probabilité d'une variable aleatoire
continue (V.A.C)
Si x=V .A.C, on a
 (Integral de Riemann) (Integral de Riemann)
où  tel que tel que  , ,  est la densité de probabilité est la densité de probabilité
B.9. Fonction de
répartition de la V.A x
Définition : Soit x une V.A sur
(Ù,á,IP), on appelle fonction de répartition de la V.A x
sur (Ù,á,IP)

B.10. Système Complet
d'événement
Les evenement A1,A2,...,An en nombre fini sont dit totalement
disjoints ou forment un système complet d'évenement dans á
ssi :
1) Ai  , pour tout i=1,2,...,n , pour tout i=1,2,...,n
2) Ai Aj= Aj= , ,

3) B.11.
Théorème de probabilités totales
Hypothèse :
(1) Soit A1,A2,...,An un système complet
d'événement
(2) Supposons qu'un autre événement B ne puisse se
produire qu'en combinaison avec l'un des événements Ai du
système complet d'événement
B=

Bibliographie
Ouvrages
- Michel Denuit et Christian Robert,
« actuariat des Assurances des
personnes (modélisations, tarification et
provisionnement) ». Edition Economica Janvier 2007.
- Mathieu Alain, « Etude du
système d'offre des soins en France ». Edition Eyrolles. Aout
2008.
- Muriel Anne :
« Probabilité et Statistique », Edition
Schaum New York, 1987.
- Luc
Arrondelle : « Epargne, assurance-vie et
retraite ». Edition Mathematica 2007
Notes des cours
- Professeur Manya, « Statistique
Descriptive », année académique 2006-2007
- Professeur Manya, « Statistique
Inférentielle », année académique 2007-2008
- Professeur Muhindo :
« Statistique appliquée aux affaires », année
académique 2007-2009.
Mémoire
- Batundu, « Etude
d'évolution des primes d'assurance vie ». Institut
Supérieur de Statistique de Kinshasa. 1995.
Webographie
- Okou
Gérard Mathieu N'KATTA, « Quelles politiques en vu d'une
amélioration de la gestion d'un portefeuille d'assurance maladie: cas de
GNA assurances ». Institut national polyechnique Félix
Houphouet Boigny. 2008. www.memoireonline.com
- www.who.com
- www.medicare.com
- www.sonas.cd
Table des
matières
Préambule
Erreur ! Signet non
défini.
Préface
3
Chapitre 1 : Généralité
sur les assurances
5
1.1. Historique
5
1.2. Définitions
6
1.3. Eléments de l'assurance
8
1.3.1. Le risque
8
1.3.2. La prime
9
1.3.3. La prestation de l'assureur
9
1.3.4. Le contrat d'assurance
10
1.4. Classification des assurances
11
1.4.1. D'après la forme
11
1.4.2. Suivant leur objet
12
Chapitre 2 : Etude du système
d'assurance maladie (cas de la France)
15
2.1. Introduction
15
2.2. L'assurance maladie produit d'une lente
évolution
15
2.3. Reforme de 1945 et ses
prolongements
17
2.4. Généralisation effective
de l'assurance maladie
18
2.5. Structure de l'assurance maladie en
France
19
2.6. Problématique de la
dépense de l'assurance maladie
19
2.7. Financement de l'assurance maladie
20
2.7.1. Source de financement de l'assurance
maladie
21
2.7.2. Impacte de l'assurance maladie sur le
chômage et la régulation économique
21
Chapitre 3 : Etude du modèle
d'assurance maladie par l'approche
23
stochastique
23
3.1. Généralités
23
3.2. Caractéristiques
supplémentaires des produits d'hospitalisations
24
3.3. Approche utilisés
24
 (3.1)
24 (3.1)
24
3.4. Modélisation
25
3.5. Interprétation
mathématique des modèles
26
3.6. Taux instantanés des
transitions
27
3.6.1. Définitions
27
3.6.2. Lien avec les probabilités de
transition
27
3.6.3. Expression des probabilités de
transition sous forme de taux de transition
28
3.7. Constance des taux instantanés
de transition
29
3.7.1. Probabilité de transition
annuelle
29
3.8. Lien avec les probabilités de
séjour
31
3.8.1. Définition
31
3.8.2. Expression des probabilités de
séjour en fonction des taux des transitions
32
3.9. Aspects techniques
32
3.9.1. Prestations des parties
32
3.9.2. Réserves
mathématiques
34
3.10. Estimation des taux de transition
35
3.10.1. Exposition au risque
35
3.10.2. Estimation brut des taux de
transition
36
Chapitre 4 : Estimation de la prime de risque
pour une prise en charge
38
dans les services de maternité et de
Gynéco au l'hôpital
38
Saint joseph de Kinshasa
38
4.1. Introduction
38
4.1.1. Estimations de nombre de transition
de l'état « actif » à l'état
« grossesse » (« accouchement »)
39
4.2. Service de Gynécologie
45
4.2.1. Estimations de nombre de transition
de l'état « actif » à l'état
« hospitalisé »
45
4.3. Estimation des probabilités de
transition
52
4.4. Estimation de la prime (28-30 ans)
55
4.5. Estimation de la prime de risques pour
les assurées de 25 à 27 ans
57
Conclusion
59
Annexe A
60
Annexe B
63
B.1. Expérience Aléatoire
63
B.2. Eventualité
63
B.3. ó-Algèbre
63
B.4. Probabilité (Définition
axiomatique)
63
B.5. Variables aléatoires
63
B.6. Processus stochastiques
64
B.7. Fonction de renouvellement simple
64
B.8. Distribution de probabilité de la
variable aléatoire x
65
B.9. Fonction de répartition de la V.A x
65
B.10. Système Complet
d'événement
65
B.11. Théorème de probabilités
totales
66
Bibliographie
67
|
|



