Analyse de l'impact de l'agrégat monétaire M3 sur l'inflation en haiti de 2000 à 2010

ANNEXES

a) Tableaux

Tableau 6 : Intervention de la BRH sur le marché des changes pendant l'exercice 2008/2009

Mois	Achats de devises			Ventes de devises
	Montant en $	Montant en gourdes	Taux moyen	Montant en $	Montant en gourdes	Taux moyen
Oct. 98	1,700,000.00	28,447,250.00	16.7337	1,450,000.00	24,249,375.00	16.7237
Nov. 98	0.00	0.00	-	250,000.00	4,164,000.00	16.6560
Déc. 98	3,055,000.00	50,684,900.00	16.5908	1,280,000.00	21,246,600.00	16.5989
Janv. 99	1,800,000.00	30,560,000.00	16.9778	275,000.00	4,634,375.00	16.8523
Fév. 99	1,600,000.00	27,165,875.00	16.9787	100,000.00	1,705,000.00	17.0500
Mars 99	8,860,000.00	149,989,525.00	16.9288	0.00	0.00	-
Avril 99	8,150,000.00	137,347,250.00	16.8524	560,000.00	9,453,500.00	16.8813
Mai 99	8,200,000.00	138,158,975.00	16.8487	200,000.00	3,368,000.00	16.8400
Juin	8,500,000.00	143,189,000.00	16.8458	1,000,000.00	16,872,500.00	16.8725
Juil. 99	3,100,000.00	52,624,000.00	16.9755	2,750,000.00	46,735,100.00	16.9926
Août 99	1,150,000.00	19,451,150.00	16.9140	2,050,000.00	34,686,150.00	16.9201
Sept. 99	0.00	0.00	-	3,500,000.00	60,116,770.00	17.1762
Total	46,115,000.00	777,617,927.00	16.8626	13,415,000.00	227,231,370.00	16.9386

Sources : BRU

84

Tableau 7 : Evolution de la masse monétaire en millions de gourdes et de l'indice des prix à la consommation d'octobre 1999 à septembre 2010.

85

Tableau 8 : estimation des paramètres du VAR(3) à partir du logiciel EVIEWS

Vector Autoregression Estimates Date: 04/15/13 Time: 13:36

Sample (adjusted): 2000M02 2010M09

Included observations: 128 after adjustments Standard errors in ( ) & t-statistics in [ ]

		DLLOGIPC				DLLOGM3
DLLOGIPC(-1) DLLOGIPC(-2)		[ [	0.379259 (0.09183) 4.13017] 0.047620 (0.09756) 0.48812]				-0.172862 [-0.90423] -0.014161 [-0.06972] (0.19117) (0.20310)
DLLOGIPC(-3)			0.046905				0.334842
			(0.08785)				(0.18289)
		[	0.53393]			[	1.83084]
DLLOGM3(-1)			0.115169				0.005950
			(0.04325)				(0.09004)
		[	2.66291]			[	0.06608]
DLLOGM3(-2)			0.087284				0.073478
			(0.04375)				(0.09108)
		[	1.99508]			[	0.80672]
DLLOGM3(-3)			0.035182				0.173005
			(0.04437)				(0.09236)
		[	0.79299]			[	1.87308]
C			0.002485				0.007956
			(0.00147)				(0.00305)
		[	1.69531]			[	2.60674]
R-squared	0.328458			0.066702
Adj. R-squared	0.295159			0.020423
Sum sq. resids	0.011441			0.049589
S.E. equation	0.009724			0.020244
F-statistic	9.863739			1.441301
Log likelihood	415.0200			321.1613
Akaike AIC	-6.375312			-4.908770
Schwarz SC	-6.219342			-4.752799
Mean dependent	0.010582			0.012821
S.D. dependent 0.011582					0.020454
Determinant resid covariance (dof adj.)					3.80E-08
Determinant resid covariance					3.40E-08
Log likelihood					737.3499
Akaike information criterion					-11.30234
Schwarz criterion					-10.99040

Sources : calcul de l'auteur, EVIEWS 5.0

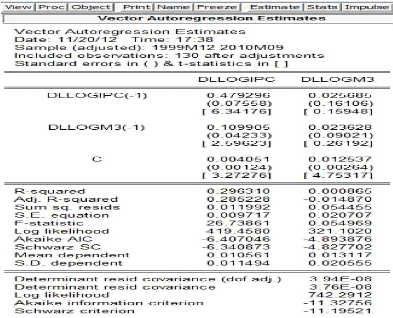
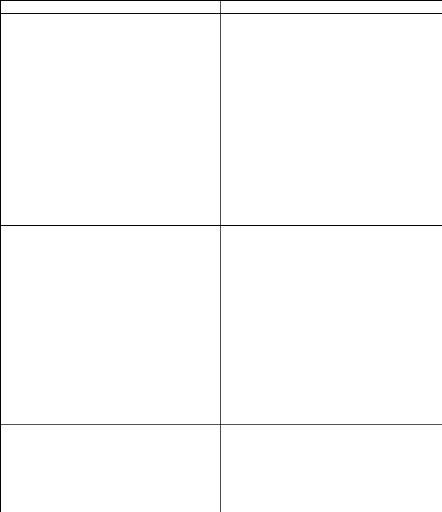
Tableau 9 : estimation des paramètres du VAR(1) à partir du logiciel EVIEWS

86

Sources : calcul de l'auteur, EVIEWS 5.0

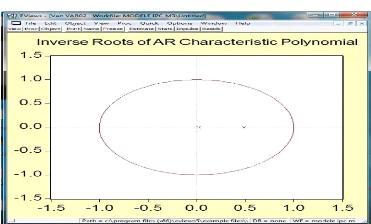
Graphique 10 : Inverse de la racine associée à la partie AR

87

Sources : Calcul de l'auteur à partir de données provenant de l'IHSI et de la BRH

Modèle 3 : Ici, on commence par :

- Estimation du modèle.

- Test de Significativité du trend. H0 : â=0 et H1 :â?0. Deux possibilités : Si Tc=Ttab ou Proba>0.05, on accepte H0, donc le trend est non significatif. Dans ce cas, on passe au modèle 2. Si au contraire, Tc>Ttab ou Proba<0.05, on rejette H0, donc le trend est significatif. Dans ce cas, on garde le modèle 3 et on effectue le test de RU.

- Test de Racine Unitaire. H0 : ö=0 ou ñ=1 (série non stationnaire)

H1 : ö<0 ou /ñ/<1 ( série stationnaire). Deux possibilites : Si ADF=Ttab, on accepte Ho, donc la série est non stationnaire. Si au contraire, ADF<Ttab, on rejette H0, donc la série est stationnaire.

Modèle 2 : Ici, on commence par :

- Estimation du modèle.

-Test de Significativité de la constante. H0 : á=0 et H1 :á?0. Deux possibilités :. Si Tc=Ttab ou Proba>0.05, on accepte H0, donc la constante est non significative. Dans ce cas, on passe au modèle 1. Si au contraire, Tc>Ttab ou Proba<0.05, on rejette H0, donc la constante est significative. Dans ce cas, on garde le modèle 2 et on effectue le test de RU

- Test de Racine Unitaire. H0 :ö=0 ou ñ=1 (série non stationnaire) et H1 : ö<0 ou /ñ/<1 ( série stationnaire). Deux possibilites : Si ADF=Ttab, on accepte Ho, donc la série est non stationnaire. Si au contraire, ADF<Ttab, on rejette H0, donc la série est stationnaire.

Modèle 1 : Ici, on effectue le test :

- Test de Racine Unitaire. H0 :ö=0 ou ñ=1 (série non stationnaire) et H1 : ö<0 ou /ñ/<1 ( série stationnaire). Deux possibilités : Si ADF=Ttab, on accepte Ho, donc la série est non stationnaire. Si au contraire, ADF<Ttab, on rejette H0, donc la série est stationnaire.

Test ADF (3 Modèles)

Modèle 3 : Ici, on commence par :

- Estimation du modèle.

- Test de Significativité du trend. H0 : â=0 et H1 :â?0. Deux possibilités : Si Tc=Ttab ou Proba>0.05, on accepte H0, donc le trend est non significatif. Dans ce cas, on passe au modèle 2. Si au contraire, Tc>Ttab ou Proba<0.05, on rejette H0, donc le trend est significatif. Dans ce cas, on garde le modèle 3 et on effectue le test de RU.

- Test de Racine Unitaire. H0 : ö=0 ou ñ=1 (série non stationnaire) et H1 : ö<0 ou /ñ/<1 ( série stationnaire). Deux possibilites : Si PP=Ttab, on accepte Ho, donc la série est non stationnaire. Si au contraire, PP<Ttab, on rejette H0, donc la série est stationnaire.

Modèle 2 : Ici, on commence par :

- Estimation du modèle.

- Test de Significativité de la constante. H0 : á=0 et H1 :á?0. Deux possibilités :. Si Tc=Ttab ou Proba>0.05, on accepte H0, donc la constante est non significative. Dans ce cas, on passe au modèle 1. Si au contraire, Tc>Ttab ou Proba<0.05, on rejette H0, donc la constante est significative. Dans ce cas, on garde le modèle 2 et on effectue le test de RU

- Test de Racine Unitaire. H0 :ö=0 ou ñ=1 (série non stationnaire) et H1 : ö<0 ou /ñ/<1 ( série stationnaire). Deux possibilités : Si PP=Ttab, on accepte Ho, donc la série est non stationnaire. Si au contraire, PP<Ttab, on rejette H0, donc la série est stationnaire.

Modèle 1 : Ici, on effectue le test :

- Test de Racine Unitaire. H0 :ö=0 ou ñ=1 (série non stationnaire) et H1 : ö<0 ou /ñ/<1 ( série stationnaire). Deux possibilités : Si PP=Ttab, on accepte Ho, donc la série est non stationnaire. Si au contraire, PP<Ttab, on rejette H0, donc la série est stationnaire.

Test PP (3 Modèles)

88

Tableau 10 : Récapitulatif des stratégies et des règles de décision des tests de racine unitaire

89

b) Présentation des résultats des différents tests de Dickey-Fuller effectués sur les séries LOGIPC et LOGM3 (en niveau et en différence première) à partir du logiciel EVIEWS 5.0 :

^{Null Hypothesis: LOGIPC has a unit root}

^{t-Statistic Prob.*}

^{Augmented Dickey-Fuller test statistic 0.087090 0.9969}

^{Exogenous: Constant, Linear Trend}

^{Lag Length: 1 (Automatic based on SIC, MAXLAG=12)}

^{Test critical values: 1% level -4.030157}

^{10% level -3.147221}

^{5% level -3.444756}

^{*MacKinnon (1996) one-sided p-values.}

^{Augmented Dickey-Fuller Test Equation}

^{Dependent Variable: D(LOGIPC)}

^{Method: Least Squares}

^{Variable Coefficient Std. Error t-Statistic Prob.}

^{Date: 12/10/12 Time: 13:30}

^{Sample (adjusted): 1999M12 2010M09}

^{Included observations: 130 after adjustments}

^{LOGIPC(-1) 0.000839 0.009635 0.087090 0.9307}

^{D(LOGIPC(-1)) 0.453664 0.080975 5.602525 0.0000}

^{C 0.006284 0.036354 0.172866 0.8630}

^{@TREND(1999M10) -6.59E-05 0.000118 -0.557720 0.5780}

^{R-squared 0.289434 Mean dependent var 0.010561}

^{Adjusted R-squared 0.272516 S.D. dependent var 0.011494}

^{S.E. of regression 0.009803 Akaike info criterion -6.381938}

^{Sum squared resid 0.012109 Schwarz criterion -6.293706}

^{Log likelihood 418.8260 F-statistic 17.10781}

^{Durbin-Watson stat 2.038036 Prob(F-statistic) 0.000000}

90

^{Null Hypothesis: LOGIPC has a unit root}

^{Lag Length: 1 (Automatic based on SIC, MAXLAG=12)}

^{t-Statistic Prob.*}

^{Test critical values: 1% level -3.481217}

^{5% level -2.883753}

^{10% level -2.578694}

^{Exogenous: Constant}

^{*MacKinnon (1996) one-sided p-values.}

^{Augmented Dickey-Fuller test statistic -2.262753 0.1857}

^{Dependent Variable: D(LOGIPC)}

^{Method: Least Squares}

^{Augmented Dickey-Fuller Test Equation}

^{LOGIPC(-1) -0.004422 0.001954 -2.262753 0.0253}

^{D(LOGIPC(-1)) 0.466231 0.077565 6.010807 0.0000}

^{C 0.025890 0.009240 2.802129 0.0059}

^{Date: 12/10/12 Time: 13:31}

^{Sample (adjusted): 1999M12 2010M09}

^{Included observations: 130 after adjustments}

^{Variable Coefficient Std. Error t-Statistic Prob.}

^{R-squared 0.287680 Mean dependent var 0.010561}

^{Adjusted R-squared 0.276462 S.D. dependent var 0.011494}

^{S.E. of regression 0.009777 Akaike info criterion -6.394857}

^{Sum squared resid 0.012139 Schwarz criterion -6.328683}

^{Log likelihood 418.6657 F-statistic 25.64531}

^{Durbin-Watson stat 2.048777 Prob(F-statistic) 0.000000}

91

^{Exogenous: None}

^{Lag Length: 1 (Automatic based on SIC, MAXLAG=12)}

^{t-Statistic Prob.*}

^{Null Hypothesis: LOGIPC has a unit root}

^{Augmented Dickey-Fuller test statistic 3.976333 1.0000}

^{Test critical values: 1% level -2.582872}

^{5% level -1.943304}

^{10% level -1.615087}

^{*MacKinnon (1996) one-sided p-values.}

^{Augmented Dickey-Fuller Test Equation}

^{Method: Least Squares}

^{Date: 12/10/12 Time: 13:32}

^{Dependent Variable: D(LOGIPC)}

^{LOGIPC(-1) 0.001010 0.000254 3.976333 0.0001}

^{D(LOGIPC(-1)) 0.538400 0.075098 7.169334 0.0000}

^{Sample (adjusted): 1999M12 2010M09}

^{Included observations: 130 after adjustments}

^{Variable Coefficient Std. Error t-Statistic Prob.}

^{R-squared 0.243640 Mean dependent var 0.010561}

^{Adjusted R-squared 0.237731 S.D. dependent var 0.011494}

^{S.E. of regression 0.010035 Akaike info criterion -6.350251}

^{Sum squared resid 0.012889 Schwarz criterion -6.306135}

^{Log likelihood 414.7663 Durbin-Watson stat 2.089920}

92

^{Lag Length: 0 (Automatic based on SIC, MAXLAG=12)}

^{t-Statistic Prob.*}

^{Null Hypothesis: D(LOGIPC) has a unit root}

^{Exogenous: Constant, Linear Trend}

^{Augmented Dickey-Fuller test statistic -6.929208 0.0000}

^{Test critical values: 1% level -4.030157}

^{5% level -3.444756}

^{10% level -3.147221}

^{*MacKinnon (1996) one-sided p-values.}

^{Augmented Dickey-Fuller Test Equation}

^{Sample (adjusted): 1999M12 2010M09}

^{Dependent Variable: D(LOGIPC,2)}

^{Method: Least Squares}

^{Date: 12/10/12 Time: 13:32}

^{@TREND(1999M10) -5.58E-05 2.39E-05 -2.332003 0.0213}

^{Included observations: 130 after adjustments}

^{Variable Coefficient Std. Error t-Statistic Prob.}

^{D(LOGIPC(-1)) -0.544760 0.078618 -6.929208 0.0000}

^{C 0.009445 0.002180 4.331590 0.0000}

^{R-squared 0.274637 Mean dependent var -4.02E-05}

^{Adjusted R-squared 0.263214 S.D. dependent var 0.011376}

^{S.E. of regression 0.009765 Akaike info criterion -6.397262}

^{Sum squared resid 0.012110 Schwarz criterion -6.331088}

^{Log likelihood 418.8220 F-statistic 24.04238}

^{Durbin-Watson stat 2.039518 Prob(F-statistic) 0.000000}

93

^{Lag Length: 0 (Automatic based on SIC, MAXLAG=12)}

^{t-Statistic Prob.*}

^{Augmented Dickey-Fuller test statistic -1.915043 0.6410}

^{Null Hypothesis: LOGM3 has a unit root}

^{Exogenous: Constant, Linear Trend}

^{Test critical values: 1% level -4.029595}

^{5% level -3.444487}

^{10% level -3.147063}

^{*MacKinnon (1996) one-sided p-values.}

^{Augmented Dickey-Fuller Test Equation}

^{Sample (adjusted): 1999M11 2010M09}

^{Dependent Variable: D(LOGM3)}

^{Method: Least Squares}

^{Date: 12/10/12 Time: 13:33}

^{@TREND(1999M10) 0.000449 0.000265 1.697009 0.0921}

^{Included observations: 131 after adjustments}

^{Variable Coefficient Std. Error t-Statistic Prob.}

^{LOGM3(-1) -0.041029 0.021425 -1.915043 0.0577}

^{C 0.432743 0.217405 1.990493 0.0487}

^{R-squared 0.036108 Mean dependent var 0.013177}

^{Adjusted R-squared 0.021047 S.D. dependent var 0.020487}

^{S.E. of regression 0.020270 Akaike info criterion -4.936682}

^{Sum squared resid 0.052593 Schwarz criterion -4.870838}

^{Log likelihood 326.3527 F-statistic 2.397485}

^{Durbin-Watson stat 1.930151 Prob(F-statistic) 0.095020}

94

^{Lag Length: 0 (Automatic based on SIC, MAXLAG=12)}

^{t-Statistic Prob.*}

^{Null Hypothesis: LOGM3 has a unit root}

^{Exogenous: Constant}

^{Augmented Dickey-Fuller test statistic -1.373908 0.5933}

^{Test critical values: 1% level -3.480818}

^{5% level -2.883579}

^{10% level -2.578601}

^{*MacKinnon (1996) one-sided p-values.}

^{Augmented Dickey-Fuller Test Equation}

^{Date: 12/10/12 Time: 13:33}

^{Dependent Variable: D(LOGM3)}

^{Method: Least Squares}

^{C 0.070600 0.041833 1.687642 0.0939}

^{Sample (adjusted): 1999M11 2010M09}

^{Included observations: 131 after adjustments}

^{Variable Coefficient Std. Error t-Statistic Prob.}

^{LOGM3(-1) -0.005245 0.003817 -1.373908 0.1719}

^{R-squared 0.014422 Mean dependent var 0.013177}

^{Adjusted R-squared 0.006782 S.D. dependent var 0.020487}

^{S.E. of regression 0.020417 Akaike info criterion -4.929700}

^{Sum squared resid 0.053777 Schwarz criterion -4.885804}

^{Log likelihood 324.8954 F-statistic 1.887624}

^{Durbin-Watson stat 1.956048 Prob(F-statistic) 0.171853}

95

^{Exogenous: None}

^{t-Statistic Prob.*}

^{Null Hypothesis: LOGM3 has a unit root}

^{Test critical values: 1% level -2.582734}

^{5% level -1.943285}

^{10% level -1.615099}

^{Lag Length: 0 (Automatic based on SIC, MAXLAG=12)}

^{*MacKinnon (1996) one-sided p-values.}

^{Augmented Dickey-Fuller test statistic 7.269761 1.0000}

^{Dependent Variable: D(LOGM3)}

^{Variable Coefficient Std. Error t-Statistic Prob.}

^{Augmented Dickey-Fuller Test Equation}

^{LOGM3(-1) 0.001192 0.000164 7.269761 0.0000}

^{Method: Least Squares}

^{Date: 12/10/12 Time: 13:33}

^{Sample (adjusted): 1999M11 2010M09}

^{Included observations: 131 after adjustments}

^{R-squared -0.007338 Mean dependent var 0.013177}

^{Adjusted R-squared -0.007338 S.D. dependent var 0.020487}

^{S.E. of regression 0.020562 Akaike info criterion -4.923129}

^{Sum squared resid 0.054964 Schwarz criterion -4.901181}

^{Log likelihood 323.4649 Durbin-Watson stat 1.926039}

96

^{Lag Length: 0 (Automatic based on SIC, MAXLAG=12)}

^{t-Statistic Prob.*}

^{Augmented Dickey-Fuller test statistic -11.01484 0.0000}

^{Null Hypothesis: D(LOGM3) has a unit root}

^{Exogenous: Constant, Linear Trend}

^{Test critical values: 1% level -4.030157}

^{5% level -3.444756}

^{10% level -3.147221}

^{*MacKinnon (1996) one-sided p-values.}

^{Augmented Dickey-Fuller Test Equation}

^{Sample (adjusted): 1999M12 2010M09}

^{Dependent Variable: D(LOGM3,2)}

^{Method: Least Squares}

^{Date: 12/10/12 Time: 13:35}

^{@TREND(1999M10) -4.71E-05 4.85E-05 -0.971557 0.3331}

^{Included observations: 130 after adjustments}

^{Variable Coefficient Std. Error t-Statistic Prob.}

^{D(LOGM3(-1)) -0.983543 0.089292 -11.01484 0.0000}

^{C 0.016037 0.003980 4.029042 0.0001}

^{R-squared 0.488684 Mean dependent var 0.000117}

^{Adjusted R-squared 0.480632 S.D. dependent var 0.028630}

^{S.E. of regression 0.020633 Akaike info criterion -4.901081}

^{Sum squared resid 0.054065 Schwarz criterion -4.834907}

^{Log likelihood 321.5703 F-statistic 60.68941}

^{Durbin-Watson stat 1.973888 Prob(F-statistic) 0.000000}

97

^{Lag Length: 0 (Automatic based on SIC, MAXLAG=12)}

^{t-Statistic Prob.*}

^{Null Hypothesis: D(LOGM3) has a unit root}

^{Exogenous: Constant}

^{Augmented Dickey-Fuller test statistic -10.97669 0.0000}

^{Test critical values: 1% level -3.481217}

^{5% level -2.883753}

^{10% level -2.578694}

^{*MacKinnon (1996) one-sided p-values.}

^{Augmented Dickey-Fuller Test Equation}

^{Dependent Variable: D(LOGM3,2)}

^{Date: 12/10/12 Time: 13:35}

^{Sample (adjusted): 1999M12 2010M09}

^{Method: Least Squares}

^{Included observations: 130 after adjustments}

^{Variable Coefficient Std. Error t-Statistic Prob.}

^{D(LOGM3(-1)) -0.974104 0.088743 -10.97669 0.0000}

^{C 0.012780 0.002146 5.956124 0.0000}

^{R-squared 0.484884 Mean dependent var 0.000117}

^{Adjusted R-squared 0.480860 S.D. dependent var 0.028630}

^{S.E. of regression 0.020628 Akaike info criterion -4.909060}

^{Sum squared resid 0.054466 Schwarz criterion -4.864945}

^{Log likelihood 321.0889 F-statistic 120.4877}

^{Durbin-Watson stat 1.978996 Prob(F-statistic) 0.000000}

98

Présentation des résultats des différents tests de Phillips-Perron effectués sur les séries LOGIPC et LOGM3 (en niveau et en différence première) à partir du logiciel EVIEWS 5.0 :

^{Null Hypothesis: LOGIPC has a unit root}

^{Exogenous: Constant, Linear Trend}

^{Adj. t-Stat Prob.*}

^{Bandwidth: 6 (Newey-West using Bartlett kernel)}

^{Phillips-Perron test statistic 0.218607 0.9980}

^{Test critical values: 1% level -4.029595}

^{5% level -3.444487}

^{10% level -3.147063}

^{*MacKinnon (1996) one-sided p-values.}

^{Residual variance (no correction) 0.000116}

^{HAC corrected variance (Bartlett kernel) 0.000279}

^{Phillips-Perron Test Equation}

^{Dependent Variable: D(LOGIPC)}

^{Method: Least Squares}

^Date: 12/10/12 Time: 13:22 ^Sample (adjusted): 1999M11 2010M09 ^Variable	^Coefficient
^Included observations: 131 after adjustments ^LOGIPC(-1)	^0.013402	^0.010448 1.282712
^C	^-0.034218	^0.039709 -0.861716
^@TREND(1999M10)	^-0.000252	^Std. Error t-Statistic ^0.000126 -1.993729	^Prob.
^R-squared	^0.106506	^Mean dependent var	^0.2019
^Adjusted R-squared	^0.092545		^0.3905
	^0.010918	^Akaike info criterion	^0.0483
^Sum squared resid	^0.015257
^Log likelihood	^407.4114	^F-statistic	^0.010516
^S.E. of regression ^Durbin-Watson stat	^1.109030	^S.D. dependent var ^Prob(F-statistic)	^0.011461 ^-6.174221

99

^{Null Hypothesis: LOGIPC has a unit root}

^{Exogenous: Constant}

^{Adj. t-Stat Prob.*}

^{Bandwidth: 6 (Newey-West using Bartlett kernel)}

^{Phillips-Perron test statistic -2.195905 0.2088}

^{5% level -2.883579}

^{10% level -2.578601}

^{Test critical values: 1% level -3.480818}

^{*MacKinnon (1996) one-sided p-values.}

^{Residual variance (no correction) 0.000120}

^{HAC corrected variance (Bartlett kernel) 0.000312}

^{Phillips-Perron Test Equation}

^{Dependent Variable: D(LOGIPC)}

^{Method: Least Squares}

^Date: 12/10/12 Time: 13:23 ^Variable	^Coefficient
^Sample (adjusted): 1999M11 2010M09 ^LOGIPC(-1)	^Included observations: 131 after adjustments ^-0.007009	^0.002111 -3.320918
^C	^0.042603	^0.009710 4.387412
^R-squared	^0.078759	^Std. Error t-Statistic ^Mean dependent var	^Prob.
^Adjusted R-squared	^0.071618		^0.0012
	^0.011043	^Akaike info criterion	^0.0000
^Sum squared resid	^0.015731	^Schwarz criterion
^Log likelihood	^405.4083	^F-statistic	^0.010516
^Durbin-Watson stat	^1.053910	^S.D. dependent var ^Prob(F-statistic)	^0.011461

100

^{Bandwidth: 7 (Newey-West using Bartlett kernel)}

^{Adj. t-Stat Prob.*}

^{Null Hypothesis: LOGIPC has a unit root}

^{Exogenous: None}

^{5% level -1.943285}

^{10% level -1.615099}

^{Phillips-Perron test statistic 5.323932 1.0000}

^{Test critical values: 1% level -2.582734}

^{*MacKinnon (1996) one-sided p-values.}

^{Residual variance (no correction) 0.000138}

^{HAC corrected variance (Bartlett kernel) 0.000469}

^Variable	^Coefficient
^Phillips-Perron Test Equation ^Dependent Variable: D(LOGIPC) ^LOGIPC(-1)	^0.002205	^0.000224 9.846570
^Method: Least Squares ^Date: 12/10/12 Time: 13:23 ^R-squared	^-0.058709	^Mean dependent var
^Sample (adjusted): 1999M11 2010M09 ^Adjusted R-squared	^-0.058709
	^Included observations: 131 after adjustments ^0.011793	^Akaike info criterion
^Sum squared resid	^0.018078	^Schwarz criterion
^Log likelihood	^396.2984	^Std. Error t-Statistic ^Durbin-Watson stat	^Prob.

101

^{Adj. t-Stat Prob.*}

^{Phillips-Perron test statistic -6.903092 0.0000}

^{Null Hypothesis: D(LOGIPC) has a unit root}

^{Exogenous: Constant, Linear Trend}

^{Bandwidth: 2 (Newey-West using Bartlett kernel)}

^{10% level -3.147221}

^{*MacKinnon (1996) one-sided p-values.}

^{Test critical values: 1% level -4.030157}

^{5% level -3.444756}

^{Residual variance (no correction) 9.32E-05}

^{HAC corrected variance (Bartlett kernel) 9.16E-05}

^Phillips-Perron Test Equation ^Dependent Variable: D(LOGIPC,2) ^Variable	^Coefficient
^Method: Least Squares ^D(LOGIPC(-1))	^-0.544760	^0.078618 -6.929208
^Date: 12/10/12 Time: 13:24 ^C	^0.009445	^0.002180 4.331590
^Sample (adjusted): 1999M12 2010M09 ^@TREND(1999M10)	^-5.58E-05	^2.39E-05 -2.332003
^Included observations: 130 after adjustments ^R-squared	^0.274637	^Mean dependent var
^Adjusted R-squared	^0.263214	^Std. Error t-Statistic	^Prob.
	^0.009765	^Akaike info criterion
^Sum squared resid	^0.012110	^Schwarz criterion	^0.0000
^Log likelihood	^418.8220	^F-statistic	^0.0000
^Durbin-Watson stat	^2.039518	^Prob(F-statistic)	^0.0213

102

^{Adj. t-Stat Prob.*}

^{Null Hypothesis: LOGM3 has a unit root}

^{Exogenous: Constant, Linear Trend}

^{Bandwidth: 4 (Newey-West using Bartlett kernel)}

^{Phillips-Perron test statistic -2.019091 0.5852}

^{Test critical values: 1% level -4.029595}

^{5% level -3.444487}

^{10% level -3.147063}

^{*MacKinnon (1996) one-sided p-values.}

^{Residual variance (no correction) 0.000401}

^{HAC corrected variance (Bartlett kernel) 0.000498}

^Phillips-Perron Test Equation ^Variable	^Coefficient
^Dependent Variable: D(LOGM3) ^Method: Least Squares ^LOGM3(-1)	^-0.041029	^0.021425 -1.915043
^Date: 12/10/12 Time: 13:25 ^C	^0.432743	^0.217405 1.990493
^Sample (adjusted): 1999M11 2010M09 ^@TREND(1999M10)	^0.000449	^0.000265 1.697009
^Included observations: 131 after adjustments ^R-squared	^0.036108	^Mean dependent var
^Adjusted R-squared	^0.021047	^Std. Error t-Statistic	^Prob.
	^0.020270	^Akaike info criterion
^Sum squared resid	^0.052593	^Schwarz criterion	^0.0577
^Log likelihood	^326.3527	^F-statistic	^0.0487
^Durbin-Watson stat	^1.930151	^Prob(F-statistic)	^0.0921

103

^{Bandwidth: 3 (Newey-West using Bartlett kernel)}

^{Adj. t-Stat Prob.*}

^{Phillips-Perron test statistic -1.314582 0.6216}

^{Null Hypothesis: LOGM3 has a unit root}

^{Exogenous: Constant}

^{5% level -2.883579}

^{10% level -2.578601}

^{*MacKinnon (1996) one-sided p-values.}

^{Test critical values: 1% level -3.480818}

^{Residual variance (no correction) 0.000411}

^{HAC corrected variance (Bartlett kernel) 0.000474}

^Phillips-Perron Test Equation ^Variable	^Coefficient
^Dependent Variable: D(LOGM3) ^LOGM3(-1)	^-0.005245	^0.003817 -1.373908
^Method: Least Squares ^Date: 12/10/12 Time: 13:26 ^C	^0.070600	^0.041833 1.687642
^Sample (adjusted): 1999M11 2010M09 ^R-squared	^0.014422	^Mean dependent var
^Adjusted R-squared	^Included observations: 131 after adjustments ^0.006782
	^0.020417	^Akaike info criterion
^Sum squared resid	^0.053777	^Std. Error t-Statistic ^Schwarz criterion	^Prob.
^Log likelihood	^324.8954	^F-statistic
^Durbin-Watson stat	^1.956048	^Prob(F-statistic)	^0.1719 ^0.0939

104

^{Exogenous: None}

^{Bandwidth: 4 (Newey-West using Bartlett kernel)}

^{Adj. t-Stat Prob.*}

^{Null Hypothesis: LOGM3 has a unit root}

^{Test critical values: 1% level -2.582734}

^{5% level -1.943285}

^{10% level -1.615099}

^{Phillips-Perron test statistic 6.520607 1.0000}

^{*MacKinnon (1996) one-sided p-values.}

^{Residual variance (no correction) 0.000420}

^{HAC corrected variance (Bartlett kernel) 0.000521}

^Variable	^Coefficient
^Phillips-Perron Test Equation ^Dependent Variable: D(LOGM3) ^LOGM3(-1)	^0.001192	^0.000164 7.269761
^Method: Least Squares ^R-squared	^-0.007338	^Mean dependent var
^Date: 12/10/12 Time: 13:26 ^Adjusted R-squared	^-0.007338
^Sample (adjusted): 1999M11 2010M09	^0.020562	^Akaike info criterion
^Sum squared resid	^Included observations: 131 after adjustments ^0.054964	^Schwarz criterion
^Log likelihood	^323.4649	^Std. Error t-Statistic ^Durbin-Watson stat	^Prob.

105

^{Bandwidth: 3 (Newey-West using Bartlett kernel)}

^{Adj. t-Stat Prob.*}

^{Phillips-Perron test statistic -11.06023 0.0000}

^{Null Hypothesis: D(LOGM3) has a unit root}

^{Exogenous: Constant, Linear Trend}

^{10% level -3.147221}

^{*MacKinnon (1996) one-sided p-values.}

^{Test critical values: 1% level -4.030157}

^{5% level -3.444756}

^{Residual variance (no correction) 0.000416}

^{HAC corrected variance (Bartlett kernel) 0.000467}

^Phillips-Perron Test Equation ^Variable	^Coefficient
^Dependent Variable: D(LOGM3,2) ^Method: Least Squares ^D(LOGM3(-1))	^-0.983543	^0.089292 -11.01484
^Date: 12/10/12 Time: 13:26 ^C	^0.016037	^0.003980 4.029042
^Sample (adjusted): 1999M12 2010M09 ^@TREND(1999M10)	^-4.71E-05	^4.85E-05 -0.971557
^Included observations: 130 after adjustments ^R-squared	^0.488684	^Mean dependent var
^Adjusted R-squared	^0.480632	^Std. Error t-Statistic	^Prob.
	^0.020633	^Akaike info criterion
^Sum squared resid	^0.054065		^0.0000
^Log likelihood	^321.5703	^F-statistic	^0.0001
^Durbin-Watson stat	^1.973888	^Prob(F-statistic)	^0.3331

106

^{Bandwidth: 3 (Newey-West using Bartlett kernel)}

^{Adj. t-Stat Prob.*}

^{Phillips-Perron test statistic -11.02465 0.0000}

^{Null Hypothesis: D(LOGM3) has a unit root}

^{Exogenous: Constant}

^{5% level -2.883753}

^{10% level -2.578694}

^{Test critical values: 1% level -3.481217}

^{*MacKinnon (1996) one-sided p-values.}

^{Residual variance (no correction) 0.000419}

^{HAC corrected variance (Bartlett kernel) 0.000472}

^Phillips-Perron Test Equation ^Variable	^Coefficient
^Dependent Variable: D(LOGM3,2) ^D(LOGM3(-1))	^-0.974104	^0.088743 -10.97669
^Method: Least Squares ^Date: 12/10/12 Time: 13:27 ^C	^0.012780	^0.002146 5.956124
^Sample (adjusted): 1999M12 2010M09 ^R-squared	^0.484884	^Mean dependent var
^Adjusted R-squared	^Included observations: 130 after adjustments ^0.480860
	^0.020628	^Akaike info criterion
^Sum squared resid	^0.054466	^Std. Error t-Statistic	^Prob.
^Log likelihood	^321.0889	^F-statistic
^Durbin-Watson stat	^1.978996	^Prob(F-statistic)	^0.0000 ^0.0000

107

Quelques tentatives à partir des séries M1 et M2 : a) Résultats obtenus à partir de M1

DLLOGIPCt = 0.509803*DLLOGIPCt-1 + 0.062282*DLLOGM1t-1 + 0.004418

(6.77247] (2.1136] (3.61161]

DLLOGM1t = -0.130265*DLLOGIPCt-1 - 0.130815*DLLOGM1t-1 + 0.015368

(-0.56798] (-1.45707] (4.12359]

Les résultats de l'équation « DLLOGIPCt » sont similaires aux résultats retrouvés dans le cadre de ce présent travail en représentant le VAR à partir de M3.

Pour la stabilité du VAR

Toutes les racines sont à l'intérieure du cercle, ce VAR est bien stationnaire.

108

Fonction de réponses aux impulsions

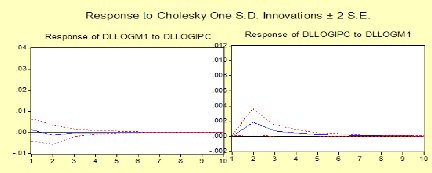
Suite à un choc de 1% sur M1, l'inflation réagit à partir de la deuxième période avec une

variation de 0.2%.

Décomposition de la variance

La variance de l'erreur de prévision de DLLOGIPC est due à 97% de ses propres innovations contre 3% de celles de DLLOGM1.

b) Résultats obtenus à partir de M2

DLLOGIPCt = 0.495975*DLLOGIPCt-1 + 0.097067*DLLOGM2t-1 + 0.004311

(6.52879] (1.86037] (3.41597]

DLLOGM2t = 0.129120*DLLOGIPCt-1 - 0.130815*DLLOGM2t-1 + 0.009473

(0.98305] (-1.45707] (4.34109]

109

La dans l'équation «DLLOGIPCt », le coefficient de DLLOGM2 n'est pas statistiquement significatif.

110

Tableau #11 : Evolution des agrégats monétaires Ml et M2 en millions de gourdes d'octobre 1999 à septembre 2010.

	1999-2000		2000-2001		2001-2002		2002-2003			2003 2004		2004-2005
Mois	Mien ME	M2enMG	Mien ME	M2enMG	M1enMG	M2enMG	M1enMG	M2enMG		M1enMG	M2enMG	M1enMG	M2enMG
Qcta re	7,389.75	16,6fi844	8,606.70	L3,491.11	9,542.35	21,206E7	..,56455	24,45229		14,137.93	3.0,7295.	16,10951	35,05759
Novembre	7,437.0D	16,8602S	9,477.52	.3,38 20	9,5E5.24	21,27235	..,391.02	24,8fi0.75		14,783,84	31,729448	16,43429	34,99251
Décembre	8,15309	17,66633	9,052.13	20,069.47	10,31323	21,92155	13,065.3	26,191.07		15,95922	33,21561	17,361.1E	36,44561
Janvier	7,986.69	17,745.13	9,259.63	20,14762	10,247 26	21,792.73	13,07921	26,656.10		15,944.71	33,59103	17,214,83	36,537.92
Février	7,77E26	17,711.43	9,716.42	20,064.44	10,584.60	22,08234	13,728.72	27,95525		15,972.43	34,040.62	17,257.69	36,85662
Mars	7,946.11	12,116.44	9,936.71	20,539.74	10,3E4.69	21,919.12	13,53227	28,208.71		1fi,146.44	34,351.13	17,74355	37,569.64
Avril	8,022.0E	12,254,29	9,695.35	20,43357	10,30265	21,27256	14,10fi56	29,08351		15,969.42	34,034.27	:7,59E62	37,622.66
Mai	7,811.44	18,241.75	9,619.01	20,388.79	10,39E65	21,840.12	13,880,80	:3,.66.18		15,401E5	33,517.19	.7,588.49	37,53233
Juin	2,048.71	12;66E21	9,242.22	20,617.16	1441122	22,260.70	14,0E7.0^4	29,22726		15,010.61	33,455.E	18,227.24	32,192.65
Juillet	8,1&0.87	18,774.44	9,980.79	20/689.69	14,67490	22,71153	14,242.37	30,063E7		15,44922	34,04128	18,624.75	38,492.11
Août	8,157.01	10,79337	3,3E0.01	21,014.04	11,24625	23,251.09	14,23..s.	3.0,201.29		15,958.47	34,300.5.	18,75G.76	38,508.73
Septembre	2.527.87	19,3E721	9,303.35	21,02755	11,237.29	23,4E254	14,158,9	30.34539		15,906.0E	34,508,80	18,9990E	38,838E4
	2005 200e		2005-2007		2007 200E		200E-2049				204E-2010
Mois	Mien ME	M2enMG	Mien ME	M2enMG	M1enMG	M2enMG	M1enMG		M2enMG		M1enMG		M2enMG
Octobre	12,91E52	35,352.24	19,253.=?	42,524.75	21,572.44	=5,235.33	25,2E7.75		50,54430		28,49E35		54,70304
Novembre	18,720.68	38,61128	=9,52.=.::	42,85fi5fi	21,805.36	=5,52L.=3	25,22521		51,029.17		28,111.45		54,2E3.42
Clkemhre	20,43E.39	40,48933	2=,03S.S2	44,625.02	23,713.29	47,2.:.SS	27,95E32		53,6E223		29,7950E		56,0E7.19
Janvier	20,448,84	44,994.43	2.0,144.fi7	44,14152	24,11950	42,253.32	27,4815.		53,04934		30,265.46		57,14653
Février	210,1E521	44,84829	.9,7G1.42	43,839.03	23,312.2fi	47,45958	27,477.03		53,715.49		31,65027		58,123.03
Mars	19,9479E	40,976.48	19,513.00	41,9859fi	24,096.0	42,37E52	27,475.07		53,33159		31,72420		59,10423
Avril	24,24357	41,35237	19,934.68	=2,28722	24,526.62	49,21050	26,373.69		52,73E68		32.795.02		60,5912fi
Mai	24,4.4.09	41,824.63	19,6133^.7	42,393.07	24,72063	49,901.37	26,447.78		52,09251		::.=9420		51,285.4E
Juin	20,24823	41,64630	19,9E033	43,21E53	24,5E455	49,222.27	26,154.44		52,4E531		33,507.77		5.,581.72
Juillet	19,43E.09	40,81952	20,16923	43,753.64	24,99506	50,39955	26,14705		52,370.44		35,03537		53,21938
Août	19,511.76	40,833.67	2.O,67463	44,113.61	26,21957	51,4902	27,117.19		52,82537		34,518.25		52,892.41
Septembre	19,56153	42,E79,24	21,2E2.78	44,732.1fi	25,139.46	54,2543fi	28,959.3E		54,24621		37,45520		S6,4fi629

Source ; BRH

111