IV.2.3- détermination du nombre de retards
optimal
Pour déterminer le nombre de retards optimal, nous allons
estimer un VAR(p) auquel nous allons ultérieurement appliquer le
critère d'optimalité.
« p » étant un nombre de retards choisis au
hasard. Soit p=3, nous obtenons le VAR qui suit :
DLLOGIPC = C(1,1)*DLLOGIPC(-1) +
C(1,2)*DLLOGIPC(-2) + C(1,3)*DLLOGIPC(-3) + C(1,4)*DLLOGM3(-1) +
C(1,5)*DLLOGM3(-2) + C(1,6)*DLLOGM3(-3) + C(1,7)
72
DLLOGM3 = C(2,1)*DLLOGIPC(-1) +
C(2,2)*DLLOGIPC(-2) + C(2,3)*DLLOGIPC(-3) + C(2,4)*DLLOGM3(-1) +
C(2,5)*DLLOGM3(-2) + C(2,6)*DLLOGM3(-3) + C(2,7)
En estimant le VAR à partir du logiciel EVIEWS 5.0, nous
obtenons les résultats suivants:
DLLOGIPC = 0.379*DLLOGIPC(-1) +
0.048*DLLOGIPC(-2) + 0.047*DLLOGIPC(-3) + 0.115*DLLOGM3(-1) + 0.087*DLLOGM3(-2)
+ 0.035*DLLOGM3(-3) + 0.002
DLLOGM3 = - 0.173*DLLOGIPC(-1) -
0.014*DLLOGIPC(-2) + 0.335*DLLOGIPC(-3) + 0.006*DLLOGM3(-1) + 0.073*DLLOGM3(-2)
+ 0.173*DLLOGM3(-3) + 0.008
En appliquant le critère d'optimalité sur ce VAR(3)
à l'aide du logiciel EVIEWS 5.0, nous obtenons les résultats
suivants :
Tableau 3 : détermination du nombre de retard
optimal
|
Lag
|
LogL
|
LR
|
FPE
|
AIC
|
SC
|
HQ
|
|
0
|
676.4971
|
NA
|
5.92e-08
|
-10.96743
|
-10.92171
|
-10.94886
|
|
1
|
698.7850
|
43.48856*
|
4.39e-08*
|
-11.26480*
|
-11.12762*
|
-11.20908*
|
|
2
|
Endogenous variables: DLLOG
701.7793
|
5.745121
|
4.47e-08
|
-11.24844
|
-11.01981
|
-11.15557
|
|
3
|
704.8988
|
5.883935
|
4.53e-08
|
-11.23413
|
-10.91404
|
-11.10411
|
|
4
|
706.1975
|
2.407301
|
4.74e-08
|
-11.19020
|
-10.77866
|
-11.02304
|
|
5
|
707.0396
|
1.533694
|
4.99e-08
|
-11.13886
|
-10.63586
|
-10.93454
|
|
6
|
709.2753
|
3.998811
|
5.14e-08
|
-11.11017
|
-10.51572
|
-10.86871
|
|
7
|
713.0659
|
6.656520
|
5.16e-08
|
-11.10676
|
-10.42086
|
-10.82815
|
|
8
|
714.2188
|
1.987181
|
5.41e-08
|
-11.06047
|
-10.28312
|
-10.74471
|
* indicates lag order selected by the criterion
Sources : Calcul de l'auteur à partir de
données provenant de l'IHSI et de la BRH
D'après les résultats précédents,
tous les critères montrent que p=1 est le nombre de retard optimal.
Maintenant il nous est possible d'estimer le VAR.
IV.2.4- écriture et spécification du VAR
La valeur du nombre de retard optimal étant
déterminée, nous allons estimer à l'aide de la MCO un VAR
d'ordre 1 noté VAR(1) dont l'écriture est la suivante :
73
Ainsi, on a :
Avec les coefficients des équations du modèle, .
Enfin, et :
les termes d'erreur.
Après la manipulation des données sur EVIEWS
5.0, nous obtenons la valeur des coefficients :
DLLOGIPCt = 0.479296*DLLOGIPCt-1 + 0.109905*DLLOGM3t-1 +
0.004051
[6.34176] [2.59623] [3.27276]
DLLOGM3t = 0.025685*DLLOGIPCt-1 + 0.023628*DLLOGM3t-1 +
0.012537
[0.15948] [0.26192] [4.75317]
Interprétation des résultats
Nous obtenons un VAR d'ordre 1, nous remarquons cependant que
les coefficients de l'équation DLLOGM3 ne sont pas
significativement différents de 0 puisque la valeur du t de Student de
ces coefficients est inférieure à la valeur critique lue dans la
table de Student au seuil de 5% soit 1.96. Par ailleurs, tous ceux de
l'équation DLLOGIPC sont significativement
différents de 0. Ceci vient corroborer le test de causalité de
Granger effectué préalablement qui confirmait que DLLOGM3
ne cause pas DLLOGIPC mais plutôt la relation
inverse. Ainsi dans le cadre de ce travail, nous mettons l'emphase sur la
première équation, soit l'équation
DLLOGIPC. D'où la sensibilité de l'IPC
au temps t, suite à une variation de 1% de M3
au temps (t-1), est de 0.11%. En outre, les valeurs de la statistique
« t de Student » des coefficients nous permettent de conclure que
l'inflation est expliquée davantage par ses valeurs passées que
par celles de la masse monétaire.
74
o Test de causalité de Granger
Granger (1959) a proposé le concept de
causalité. La notion de causalité joue un rôle primordial
en économie dans la mesure où elle permet de mieux comprendre les
relations entre les variables. Considérons deux variables Y1t
et Y2t. On dit que Y1t
cause Y2t au sens de Granger si la
prévision de Y2t fondée sur la connaissance des
passés conjoints de Y1t et Y2t
est meilleure que celle fondée sur la seule connaissance du
passé de Y2t.
Théoriquement, la mise en évidence de relations
causales entre les variables économiques fournit des
éléments de réflexion propices à une meilleure
compréhension des phénomènes économiques. De
manière pratique, la mise en évidence des relations causales est
nécessaire à la formulation correcte des politiques
économiques. En effet, connaître le sens de la causalité
est aussi important que mettre en évidence une liaison entre les
variables économiques.
Hypothèse du test de causalité de
Granger
ne cause pas Y2t, si l'hypothèse suivante
est acceptée H0 :
Y ne cause pas Y1t, si
l'hypothèse suivante est acceptée H0 :
2t
Règle de décision au seuil a = 5%
:
Si la p-value > 5%, alors on accepte l'hypothèse H0
Calcul et conclusion du test :
Le logiciel EVIEWS nous fournit les résultats suivants
:
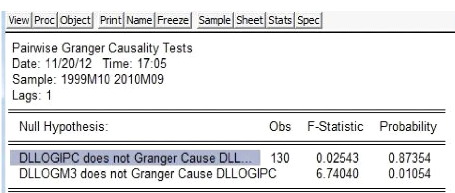
Tableau 4 : test de causalité de
Granger
75
Source : Calcul de l'auteur à partir de
données provenant de l'IHSI et de la BRH
L'hypothèse selon laquelle DLLOGM3 ne
cause pas DLLOGIPC est rejetée, donc la variation de la
masse monétaire a une influence sur la variation du niveau
général des prix. Toutefois l'hypothèse selon laquelle
DLLOGIPC ne cause pas DLLOGM3 est
acceptée ; en témoigne la probabilité qui lui est
associée (elle est supérieure à 5%, soit 87%).
| 


