3.1 Solution avec deux jours de repos
consécutifs
employés qui commencent à travailler le lundi ,
ceux qui commencent à travailler le
mardi ,..., et ceux qui commencent à travailler le
dimanche . Ainsi, selon la section
précédente, nous déduisons le modèle
mathématique complet voir tableau 12 :
La solution optimale obtenue indiquera le nombre optimal
d'employés prévus pour chaque jour de la semaine.

Table 12. Schéma de 5 jours de travail par semaine et
deux jours de repos consécutifs
Le nombre minimum requis d'employés de l'organisation est
alors :
3.2 Solution avec deux jours de repos
non-consécutifs
Dans cette étape, nous allons considérer que
chaque employé travaille cinq jours pas nécessairement
consécutifs et prend deux jours de repos par semaine. Pour ce faire,
nous considérons que la solution optimale obtenue dans la
première étape est une solution utilisable dans la
deuxième étape.
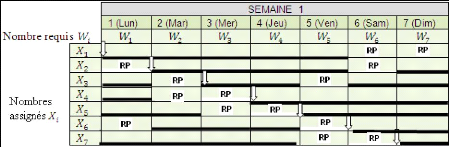
Table 13. Schéma de 5 jours de travail par semaine et
deux jours de repos non-consécutifs
Ainsi, nous supposons en premier lieu que le nombre des
employés requis le premier jour est fixe et puis nous allons supprimer
ces employés qui seront en repos dans la solution finale.
Nous supposons les variables de décision des variables de
décision binaires, où j
représente le nombre de jours (de telle sorte que 1 =
lundi, 2 = mardi, ..., et 7 = dimanche) et m
représente le nombre assigné des employés
(m = 1, 2, ..., est le nombre minimum des
employés obtenus
dans l'étape 1.
3.3 Solution avec un jour de repos
Supposons que chaque employé travaille six jours par
semaine, et prend un jour de repos RP. Afin de résoudre ce
problème, nous supposons que le nombre d'employés
nécessaires pour chaque jour de la semaine se diffère selon la
charge de travail. Donc il est nécessaire de déterminer les
capacités humaines à assigner pour chaque jour j tous en
réduisant les coûts.
|
SEMAINE 1
|
|
Jours j
|
1 (Lun)
|
2 (Mar)
|
3 (Mer)
|
4 (Jeu)
|
5 (Ven)
|
6 (Sam)
|
7 (Dim)
|
|
Nombre requis
|
|
|
|
|
|
|
|
|
Nombre assigné
|
|
|
|
|
|
|
|
Table 14. Les nombres requis et nécessaires des
agents
Le modèle mathématique est formulé en
prenant en compte le nombre des employés qui commencent à
travailler le lundi , ceux qui commencent à travailler le mardi ,..., et
ceux qui commencent à travailler le dimanche
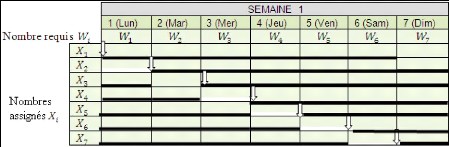
Table 15. Schéma de 5 jours de travail par semaine et
deux jours de repos non-consécutifs
La solution optimale obtenue indiquera le nombre optimal
d'employés prévus pour chaque jour de la semaine.
4 Les résultats obtenus et les axes pour la future
recherche : 4.1 Les résultats obtenus
Dans le chapitre précédent, nous avons
proposé une fonction linéaire qui permet de planifier les
employés, mais sans tenir compte les jours de repos :
|
B (T) = - [S ( , p) + S ( , p)]
|
|
Avec :
S ( , p) Nombre d'agents à la fin de la vacation du
type Nombre des employés affectés à la vacation ; Nombre
des employés nécessaires pendant la période du
chevauchement T; Nombre des employés nécessaires pendant
l'intervalle de temps p;
p Un période de temps dans un jour
donnée;
i Types des vacations;
T La période du chevauchement entre deux vacations
successive et
Le nombre de postes actifs au temps
La demande au temps
|
En effet, suite à la grande charge des compagnies
d'assistance aérienne, nous allons suppose que les employés aient
droit qu'à un seul jour de repos :
Dans ce cas notre la résolution mathématique
proposée est la suivante :
B (T) = - [S ( , p) + S ( , p)]
Avec :
S ( , p) Nombre d'agents à la fin de la vacation du
type
Nombre des employés affectés à la
vacation ;
Nombre des employés nécessaires pendant la
période du chevauchement T;
Nombre des employés nécessaires pendant
l'intervalle de temps p;
p Un période de temps dans un jour
donnée;
i Types des vacations;
T La période du chevauchement entre deux vacations
successive et Le nombre de postes actifs au temps
La demande au temps
4.2 Les axes pour la future recherche: compétence
et répartition des tâches
Suivant une étude menée par (Letouzey, 2001) sur
19 entreprises afin d'obtenir leur avis sur le problème d'affectation
des opérateurs. Cette étude a montré que la gestion du
personnel, en fonction de leurs compétences, est importante pour les
leaders de l'industrie. 79% des entreprises pensent que la gestion du personnel
est utile ou essentielle en ordonnancement.
Pour ce faire, la gestion des compétences
représente un enjeu stratégique pour beaucoup d'entreprises. Il
ne suffit plus d'avoir des compétences disponibles au sein de
l'entreprise, il faut être en mesure de déterminer les besoins
(recrutement, formations,...) (Harzallah et al., 2001). Afin de gérer de
manière plus flexible et équitable la répartition des
tâches entre les employés. Dans ce cadre, nous notons que les
compétences peuvent être soient :
- Des compétences génériques :
utilisées dans différentes situations professionnelles,
- Des compétences spécifiques : celles-ci sont
liées au domaine et au secteur d'activité.
De plus, les compétences peuvent être
identifiées à la fois sur la tâche (compétences
requises : compétences nécessaires pour la réalisation de
la tâche, de missions ou d'actions stratégiques) et sur l'agent
(compétences acquises : compétences que possède l'agent).
De ce fait, dans les futures recherches, nous pouvons tenir compte les
compétences d'employés lors de la planification d'horaire ainsi
que la répartition des tâches. L'intervention le jour de
l'opération (stratégie en temps réel) ne sera pas
traitée dans ce mémoire.
| 


