4.2 Optimisation de l'algorithme
d'énumération des vacations
Les vacations envisageables doivent être
énumérées en tenant compte du volume de la couverture afin
de réduire le nombre des agents et par conséquent, réduire
le coût de vacation. Comme nous avons déjà vu les vacations
peut se chevaucher ce qui permet d'utiliser les employés de deux
vacations dans un travail commun.
Par exemple si la vacation de matin (M) débute à
8h et termine à 16h et la vacation de soir (E) débute à
14h et termine à 22h, il aura un chevauchement de deux heures entre 14h
et 16h et pendant lesquels nous pouvons utiliser les employés des deux
vacations (voir figure 22).

Figure 22. Exemple de chevauchement des vacations de matin M et
soir E
Ainsi, nous rappelons que la version la plus commune du
modèle de Dantzig qui tient compte les aspects de coûts
liés aux vacations est la suivante :
En effet, afin d'optimiser l'énumération des
vacations V tenant compte de la couverture
de la période t et la vacation , il
est nécessaire de déterminer la valeur de
la demande pendant
la période t et la vacation
Pour se faire nous supposons que le nombre des vols
reflète le volume de la demande, par exemple, si nous avons à 5h
quatre vols nous supposons que nous avons une demande égale à
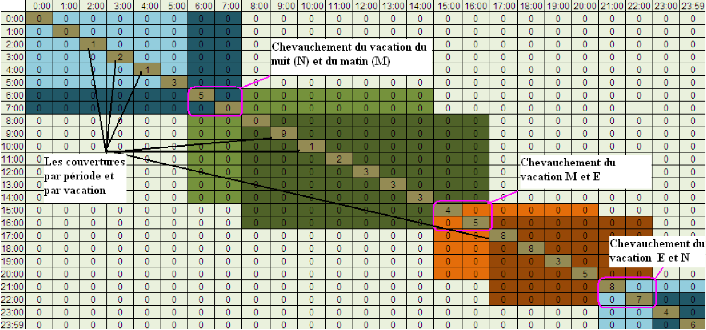
quatre agents, voir la matrice de couverture (figure 23).
71
Figure 23. Matrice de couverture journalière

72
4.3 L'algorithme d'énumération
proposée
Afin d'assurer la couverture, nous proposons trois vacations
le matin (M) qui commence soit à 6 h ou 8 h et se termine successivement
soit à 14h ou 16h, (E) soir qui commence soit à 14 h ou 16 h et
se termine successivement soit à 20 h ou 22 h, (N) nuit qui commence
soit à 20 h ou 22 h et se termine successivement soit à 6 ou 8
h.
Nous remarquons que ces vacations peuvent se chevaucher
(figure 24) et dans la période de chevauchement, nous pouvons utiliser
les agents des deux vacations.
Figure 24. Chevauchement des vacations
Ainsi à l'aide des algorithmes génétiques
multi-objectifs plus précisément à l'aide de la notion
Rang de dominance, nous pouvons choisir de chevaucher ou non deux vacations. En
effet, la stratégie Rang de dominance consiste à associer
à chaque vacation un rang proportionnel au nombre de vacations qui la
dominent. De ce fait, une vacation sera meilleure qu'une autre si elle a un
rang plus petit. Nous proposons une méthode dans laquelle chaque
vacation est rangée en fonction du nombre des vacations qui le
dominent.
En effet, une vacation Va E V1 , en domine une
autre si elle est meilleure vis-à-vis de l'ensemble des critères
indépendamment les uns des autres, avec i = {1..3} (1 matin,2
soir et 3
nuit) et avec a les possibilités
qu'une vacation peut avoir (vacation matinée peut être Vml:
débute a 6h et se termine à 14h, Vm2 :
débute a 7h et se termine à 15h, ou Vm3 : débute a 8h et
se termine à 16h) . Le concept de dominance peut être
illustré par la figure 25.
En s'appuyant sur ce concept de dominance, nous utilisons une
fonction de notation permettant de prendre en compte le rang de la vacation et
le nombre des vacations ayant même rang.
Soit une vacation à la génération ,
dominée par vacations. Le rang de cette
vacation est Rang = 1+ . Toutes les vacations non dominées
sont de rang 1 (les
meilleurs).
Exemple :
Soient les vacations , et trois types de vacation matinée
dont :
- débute a 6h et se termine à 14h,
- débute a 7h et se termine à 15h,
- débute a 8h et se termine à 16h,
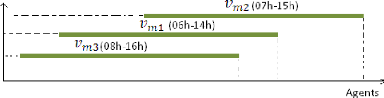
Figure 25. Exemple de dominance des vacations matinée Le
tableau de dominance est le suivant :
|
Vacations
|
Dominé par
|
Rang
|
|
|
2
|
|
et
|
3
|
|
Aucun
|
1
|
Table 6. Tableau de dominance des vacations matinée
73
La meilleure vacation à choisir qui réduit le
coût est de Rang 1.
En effet, le modèle proposé compte le nombre des
salariés à chaque vacation, de telle sorte que les besoins par
intervalle P sont satisfaits, tout en minimisant le
coût total des affectations.
Pour se faire nous supposons que S ( , p)
est le nombre des agents sur une vacation du
type qui se termine à la fin de l'intervalle
p. En effet S ( , p)
reflète le nombre max des
agents sur une vacation dont
S ( , p) égal au Max B ( ,
p). Et nous supposons que B(T)
est le nombre des agents sur la période de chevauchement
T entre deux vacations successive
et (comme indiqué dans la figure 27) et dont B(T) =
-[S ( , p) + S ( , p)] .
Ainsi, fin d'éviter les sureffectifs nous faisons appel
au modèle de Brusco et Johns qui
minimise au maximum le ratio de la demande et de sureffectifs
dont est le nombre
de postes actifs au temps est la demande au temps . Mais afin
d'éviter le manque
.
d'effectif nous proposons un modèle qui au minimum
égalise le nombre d'effectifs à la demande dans une
période de temps p :
Cependant, la charge de travail dans les compagnies
d'assistance aérienne nécessite des différentes
compétences qui doivent être représentées à
l'aide des courbes de demande distinctes, en tenant compte des qualifications
exigées, afin de créer des vacations qui peuvent la couvrir.

Figure 26. Des courbes de demande distinctes selon les
services
74
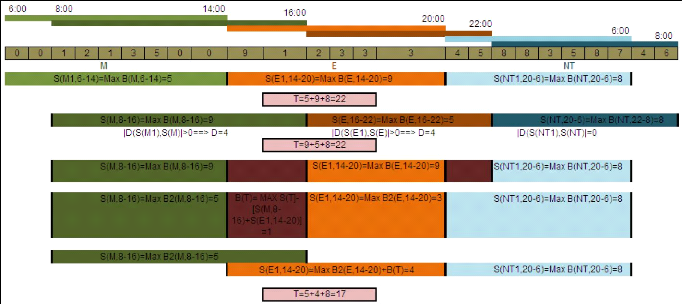
75
Figure 27. Le principe de l'algorithme d'optimisation
76
Et comme nous avons déjà annoncé dans le
cas d'un effectif hétérogène pour un ensemble de vacations
de travail le problème d'affectation doit être résolu afin
de trouver un compromis entre les sureffectifs et le manque de personnel. Nous
notons, que le problème de planification de la main-d'oeuvre
hétérogène peut être modélisé comme
suit :
En effet nous ne tenons compte du nombre des agents dans la
période du chevauchement que si la différence D entre le
nombre des agents de la vacation vti (par exemple vacation du matin M)
noté S(vti) et le nombre des agents de la vacation
v ( r e e le c tion du tin v noté S(v )est
supérieure à zéro :
)
Dans ce cadre nous proposons la fonction linaire suivante :
|
B (T) = Max B(p)- [S
(v1, p) + S (v1+1, p)]
|
|
Avec
S ( , p) Nombre d'agents à la fin de la vacation du
type durant l'intervalle de temps p ; Nombre des employés
affectés à la vacation ;
Nombre des employés nécessaires pendant la
période du chevauchement T; Nombre des employés
nécessaires pendant l'intervalle de temps p; p Un période de
temps dans un jour donnée;
i Types des vacations;
T La période du chevauchement entre deux vacations
successive et Le nombre de postes actifs au temps
La demande au temps
|
77
| 


