1.3 Le processus de dimensionnement
Pour ce faire, le dimensionnement peut être
subdivisé en des sous-problèmes. En effet, Baker cite trois
sous-problèmes :
- Le premier sous problème est la programmation de jour de
repos, il consiste à déterminer les jours sans travail (ou de
manière analogue les jours ouvrables) pour chaque employé. - Le
deuxième sous-problème détermine les horaires de travail
pour chaque journée.
- Le troisième sous-problème représente la
combinaison des deux premiers problèmes.
Cependant, Tien (1982) présente une procédure
plus détaillée en cinq étapes plus pour élaborer
l'ordonnancement :
- Prévision de la demande : détermine
le nombre de travailleurs requis pour garantir une meilleure la qualité
de service. L'usage habituel consiste à imposer une contrainte de
58
qualité de service identique pour chaque période de
la journée. Cette contrainte est, par la suite, convertie en nombre
d'effectifs nécessaire
- Détermination de l'effectif minimal :
détermine la taille totale de la main d'oeuvres nécessaires
pour satisfaire la demande tout en minimisant le coût salarial et en
respectant les contraintes de qualité de service.
- Détermination du nombre optimal de salariés
à affecter à chaque vacation.
- Positionnement des jours de repos de chaque
salarié.
- Détermination du planning de chaque
employé.
Cette subdivision illustre l'introduction progressive des
détails dans le processus décisionnel et la complexité de
chaque étape.
2 Le dimensionnement de l'effectif et les vacations 2.1
Le dimensionnent de l'effectif
Avant de pouvoir planifier l'emploi du temps d'une
équipe, il est nécessaire de connaître sa taille. Dans la
littérature scientifique, de nombreux auteurs proposent des
méthodes de calcul de la borne inférieure avec des règles
de travail contraignantes. Burns et Carter ont été les premiers
à proposer une méthodologie basée sur le calcul de
plusieurs bornes inférieures (charge de week-end, charge totale de la
semaine et charge maximale journalière), la taille étant le
maximum de ces bornes.
Ils ont considéré le cas d'une seule vacation
par jour et le besoin est d(j), J=1 pour le dimanche,..., 7 pour le samedi.
D = nombre total de salariés, D=Max(d(1),...,d(7)).Hun94 propose
une méthode de calcul de la taille minimale d'une équipe. Chaque
jour il y a V vacations (ex. J=3 pour le matin, 2=soir et 3=nuit).
Pendant la semaine, il faut au moins D(v) personnes sur la
vacation v pour v=1,..., V.
Nous nous s'intéressant à la tournée de
type 3*8 dont chaque jour dispose d'au moins
3 vacations et puisque les compagnies d'assistance travaillent
tous les jours le nombre des
plages requis = 3 (nombre des vacations / jour)* 365
(nombre de jours par ans) = 1095. Ces plages doivent être couvrir
par un certain nombre d'agents.
Cependant l'agent travaille 365 moins quatre jours de
repos par mois de travail, si l'agent a droit à un jour de repos par
semaine, et moins le congé annuel 30jrs. Donc l'agent travaille
365-4*11(jours de repos pars ans) - 30(jours de congé annuel) = 291
jours (ou vacation).
De ce fait, afin d'assurer un service 24/24 toute
l'année nous sommes besoin de 1095/291=3.76 donc au minimum
4 agents par jour. Cependant, le nombre des agents
nécessaires doivent satisfaire les besoins en termes de
plages à couvrir. Pour ce faire, nous referons à une semaine type
et à travers laquelle nous déterminons les plages
nécessaires (voir figure 17). Si nous avons N lignes de plages
d'horaire nous aurons en tout 7*N besoins par
semaine, soit 365*N par ans.
Exemple
Soit N lignes de plages d'horaire par semaine
=5
Le nombre des agents nécessaires par semaine égale
à :
agents.
=
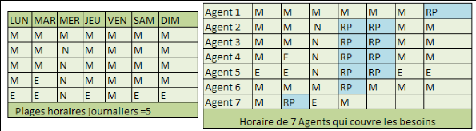
59
Figure 17. Besoins par semaine type
60
Cependant dans le cadre aérien le nombre des agents
nécessaires diffèrent d'un jour à un autre dont les
besoins se diffèrent d'un jour à un autre dans une semaine.
Afin de satisfaire les besoins, nous referons à une
semaine type et nous calculons les plages horaires totales à satisfaire
(voir figure 18).
Si nous avons N plages d'horaire par semaine nous aurons
en tout 52 (nombres des semaines par ans)* N par ans.
Exemple
Soit N plages d'horaire par semaine =62
Le nombre des agents nécessaires par semaine égale
à :
=
agents.

Figure 18. Plages horaires par semaine type
Cependant, la planification d'un personnel
hétérogène dans le cas des compagnies d'assistance tient
compte que tous les employés sont productifs mais avec des
capacités
61
différentes dont le personnel expérimenté
peut être capable d'effectuer des tâches plus avancées, en
plus de le travail de base. Pour décrire le niveau de cohésion
entre les exigences du service
et la qualification du personnelles (capacités) , nous
pouvons utiliser la fonction
suivante déjà citée :
| 


