Estimation non-paramétrique par noyaux associés et données de panel en marketing

4.2.3 Noyau associe binomial negatif

Nous rappelons _qu'une loi binomiale né_gative de paramètres s et p, BN(s,p) est une loi discréte définie sur le support N de fonction de masse de probabilité gBN(s,p) telle _que

gBN(s,p)(x) = (x + s)! ps (1 p)^x.

x!s!

Si X est une variable aléatoire _qui suit la loi binomiale né_gative, alors lespérance et la variance sont respectivement

E(X) = s(1 - p)/p et V ar(x) = s(1 - p)/p².

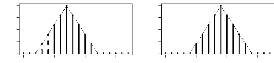
Soit KBN(x+1,(x+1)/(2x+1+h)) le no_yau associé a la variable aléatoire KBN(x+1,(x+1)/(2x+1+h)) de loi binomiale né_gative défini sur le support ?x,h = N tel _que

,

KBN(x+1,(x+1)/(2x+1+h))(y) =

(x + y)! x + h y x + 1 )x+1

y!x! 2x + 1 + h 2x + 1 + h

on x et y appartiennent a N et h est strictement positif. Nous vérifions _quil sa_git dun no_yau associé

i.N n N = N=6 Ø.

?x?x,h = ?_xN = N.

E(KBN(x+1,(x+h)/(2x+1+h))) = x+h ~x_quand h ? 0.

iv.V ~2x+1+h ~

ar(KB(x+1,(x+h)/(x+1))) = (x + h) < 8.

x+1

~

v.h ? 0 V ar(KB(x+1,(x+h)/(x+1))) = x ^~2x+1 .

x+1

Pour notre même échantillon de variables aléatoires nous donnons lestimateur fn de f a no_yau associé binomial né_gatif défini sur?x,h = N comme étant

FIG. 4.7 -- Illustration du no_yau associe binomial né_gative pour h = 0.1 et x varie

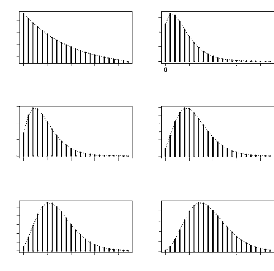
y

y

x=0

?

?

?

?

?

?

?

?

?

?

?

?

?

? ? ? ? ? ? ?

0 5 10 15 20

x=2

?

?

?

?

?

?

?

?

?

?

?

? ? ? ? ? ? ? ? ? ? ?

0 5 10 15 20

x=5

x=1

5 10 15 20

x=4

?

?

?

?

?

?

?

?

?

?

?

?

? ? ? ? ? ? ? ?

0 5 10 15 20

x=7

0.02 0.06

Probab(y)

0.00 0.05 0.10 0.15

Probab(y)

0.00 0.10

0.00 0.06 0.12

?

?

?

?

?

? ?
? ?

?

?

?

?

?

?

?

?

?

?

? ? ? ?

0 5 10 15 20

? ?
? ?

?

?

?

?

?

?

?

?

?

?

?

? ? ? ? ? ? ?

0 5 10 15 20

0.00 0.04 0.08

0.00 0.04 0.08

Probab(y)

?

?

?

?

?

?

? ?

? ? ? ? ? ? ? ? ? ?

?

?

?

avec x E N et h E R^*₊ .

Le ibiais de cet estimateur est

Biais {:fi_i(x)} = h f ⁽¹⁾ (x) + ²¹ (x + h) (2x x + 1 + 1 + h f ⁽²⁾ (x)+o(h).

D'apres (4.9), la variance est

1 2x + h^x x + 1 )x+1

nx!( 2x + 1 + h

V ar {:fi_i(x)} =

2x + 1 + h f(x).

En final, le MISE est la somme des deux derniers resultats. IlII est e_gal à

MIS E(n,h, f) = 1 E n xEN

2 ( x + h^x x + 1 V^+1 \ x! 2x + 1 + h) ( 2x + 1 + h) f(x)

2

+ E {h f ⁽¹⁾ (x) + ₂(x + h) (2x x + 1 ₁+ h f(2) (x) + o(h) } .

xEN

4.2.4 Noyau associe triangulaire

EnsereferantauxtravauxdeKokonend_jietSen_gaKiesse(2007)surlesdistriibutions trian_gulaires discretes, nous rappelons _quune loi trian_gulaire T_a,h_,c de parametres a

4.2. NOYAU ASSOCIR DISCRET POUR DES DONNRES DE COMPTAGE 79

et c dans N et h dans R+ est une loi discrete centrée en c et de bras a défini sur ?a,c = {c,c #177; 1, . . . ,c #177; a} de fonction de masse de probabilité:

Pr (Ta,h,c = y) =

(a + 1)^h - |y - c|^h P(a,h)

,

on P(a,h) est la constante de normalisation telle _que

a

P(a,h) = (2a + 1)(a + 1)^h - 2 i=0 i^h.

Nous remar_quons _que le cas h = 1 correspond a la variable aléatoire trian_gulaire s_ymétri_que. Le cas h = 0 n'est pas défini en c et en particulier, si h = 0 nous nous retrouvons la loi de Dirac d'espérance c. Si h tend vers l'infini, nous trouvons la loi uniforme Pour des entiers non nuls h ? R*, la constante de normalisation peut s'écrire:

P(a,h) = (2a + 1)(a + 1)^h - 2

a i=0

(-1)^h--i+1)h!Bh--i+1 i!(h - i + 1)! ai,

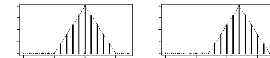
on Bh--i+1 est le nombre de Bernoulli. La fi_gure 4.8 présente l'allure de la densité trian_gulaire par rapport aux autres no_yaux discrete _que nous avons étudié.

Si X est une variable aléatoire _qui suit la loi trian_gulaire alors lespérance et la variance sont respectivement :

ih+2) .

a

E(X) = c et V ar(X) = 2E P(a,h) 3

i=0

1 a(a + 1)^h+1(2a + 1)

La loi Ta,h,c est s_ymétri_que autour de sa mo_yenne De plus la variance ne dépend pas de c.

Soit _KT(a,h,x) le no_yau trian_gulaire associé a la variable aléatoire KT(_a,h_,x), défini sur {x,x #177; 1, . . . ,x #177; a} et donné par

(a + 1)^h - |y - x|^h

KT(a,h,x)(y) = (2a + 1)(a + 1)^h - 2 Eaj=0 jh,

avec x ? N, h > 0 et a ? N.

Nous nous assurons des diférents points de la définition 1

i.{x,x #177; 1,...,x #177; a} n N = {x,x #177; 1, . . . ,x #177; a} =6 Ø. ii.?xEN {x,x #177; 1, . . . ,x #177; a} = N.

iii.E (KT (a,h,x)) = x.

iv.V ar (KT(

Nh#177;if2_a

(a(a+1) k ) 2 _E 3a. ₀ jh+2)

< 8.

a,h,x)) = P(a¹ ,h) 3

v.Lors_que h ? 0, la variance de KT(_a,h_,x) tend aussi vers 0. En effet, ce résultat a été obtenu dans la proposition (2.4) des travaux de Kokonend_ji, Sen_ga Kiessé et Zocchi (2007). Dans cette proposition, nous montrons _que la variance de la variable aléatoire conver_ge vers une loi de Dirac ce _qui impli_que une variance nulle (voir aussi la remar_que 2.3(ii))

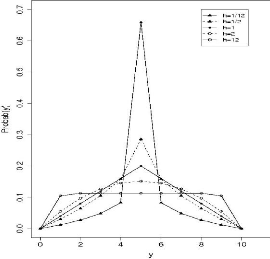
FIG. 4.8 -- ???str?t?? ?? ?\u9313‡A?? ?ss??e tr???_?????r? _??r ??_?ér??t?e ?????rr ?? h?

Soit X1, ... ,X_n l'échantillon de variables aléatoires i.i.d . de densité f inconnue définie

b

sur N. Nous donnons l'estimateur f_n de f a no_yau associé trian_gulaire défini sur ?x,h =

{x,x #177; 1, . . . ,x #177; a} comme étant:

^bfn(x) = 1 n

Xn i=1

KT(a,h,x)(Xi)

1
n

=

_Xn
i=1

(a + 1)^h - |Xi - x|^h

(2a + 1)(a + 1)^h - 2 Eaj=0 jh,

avec x ? N, h > 0 et a ? N. Le no_yau KT(_a,h_,x) est le no_yau associé défini sur ?a,x,h = {x,x #177; 1, . . . ,x #177; a} . Nous remar_quons _que le support du no_yau associé ne dépend pas de h. Si a = 0, alors ?0,x = {x} et ?x?0,x = N. Par contre, si a =6 0 nous avons

?x?N?a,x = {-a, . . . , - 1} ? N. (4.16)

Le fait _que le support du no_yau discret trian_gulaire (4.16) a a =6 0 fixé contienne strictement N induit un biais de bordure a _gauche du support de f. Nous _y remédions en modifiant le bras a par a0 de sorte _que, ?a0 nous avons

?x?N?a0,x = N.

4.2. NOYAU ASSOCIR DISCRET POUR DES DONNRES DE COMPTAGE 81

de 0, 1 ou 2), nous considerons le bras modifie a0 de a tel _que ?k ? N \ {0} donne et x ? N, nous avons

a0 = k ? a =

{

j si x = j ? {0,1, . . . ,k - 1} k si x ? {k,k + 1, ...} .

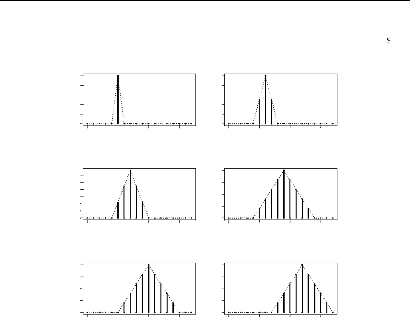
Nous illustrons ce probleme du biais de bordure dans les fi_gures 4.9 et 4.10 Nous avons fixe h = 1, a = 4 et a0 = 4.

FIG. 4.9 -- ???str?t?? ?? ?\u9313‡A?? ?ss??( r???_?????r? ??s ???_???t?? ?? ?b?a

i=0

x=0 x=1

?

?

?

?

?

?

?

? ? ? ? ? ? ? ?

?

?

- 5 0 5 10

- 5 0 5 10

?

?

?

?

?

?

?

?

? ?

? ? ? ? ? ? ?

0.00 0.10 0.20

Probab(y)

0.00 0.10 0.20

x=2 x=4

?

?

?

?

?

?

? ? ?

? ? ? ? ? ?

- 5 0 5 10

?

?

?

?

?

? ? ? ?

?

? ? ? ? ?

- 5 0 5 10

Probab(y)

0.00 0.10 020

0.00 0.10 020

x=5 x=7

Probab(y)

0.00 0.10 0.20

?

? ? ? ? ? ?

?

?

?

?

?

?

?

? ? ?

0.00 0.10 0.20

?

? ? ? ? ? ? ? ?

?

?

?

?

?

?

?

- 5 0 5 10 -5 0 5 10

y y

Le biais de cet estimateur est

Biais { i_n(x)} = 2 P(a,h)

1 1 ( a(a + 1)^h+1(2a + 1) 2 ctih+2) f⁽²⁾(x) + o(h).

3

D'apres (4.9), la variance est

x=0

x=1

? ? ? ? ?

?? ? ? ? ? ? ? ? ? ? ?

FIG. 4.10 -- ???str?t?? ?? ?\u9313‡A?? ?ss??e tr???_?????r? ???? ???_???t?? ?? ?b?a

x=2

?

?

?

?

?

? ? ? ? ?

? ? ? ?? ? ? ?

- 5 0 5 10

x=4

?

?

?

?

?

?

?

? ? ? ?

?

? ? ? ? ?

- 5 0 5 10

0.00 0.10 0.20

x=5

?

?? ? ? ? ?

?

?

?

?

?

?

?

? ? ?

- 5 0 5 10

y

x=7

?

?

?

?

?

?

?

? ? ? ? ? ? ? ?

- 5 0 5 10

y

0.00 0.10 0.20

Probab(y)

0.00 0.15 0.30

0.00 0.10 0.20

Probab(y)

- 5 0 5 10

- 5 0 5 10

?

? ? ? ? ? ? ? ? ? ?

?

?? ? ? ?

0.0 0.2 0.4

Probab(y)

0.0 0.4 0.8

on P(a,h) = (2a + 1)(a + 1)^h - 2 E;₌₀ j^h.

En final, le MISE est la somme des deux derniers resultats.III est e_gal

(a + 1)^h E MISE(n,h,f) = nP(a,h) x?N

f(x)

a

+ v, { 1 1 ( a(a + 1)^h+1(2a + 1) 2 E ih+2) f⁽²⁾(x) + o(h)

x?N

i=0 }2

2 P(a,h) 3

f. Remar_ques:

a. \u9670·?s r???r_q??s _q???? ?\u9312‡@?st? ??s ??s ??s?rèt?s _q?? ?? _??????t _??a et? ?as??i?e à ????? ?\u9313‡A?? ??s?r?t ?t?????t ?? ?? ???_?r?? ??s?rrt?? ?? ?_??e_? ? ??u ??n??de?n ?? ?? ???_?r?? ??s?ret? ???tre? ?? x ?t ?? ??r_???r 2a ? ?? ?\u9313‡A?? ?ss??e U_x,a ?e_??? s?r ?x,a = {x,x #177; 1,... ,x #177; a} s?é?r?t ???? s??t?

1

U_x,_a(y) =

2a + 11x,x#177;1,...,x#177;a(y),

ù y ?st ???s N? \u9670·?s ?_??r????s _q?? ??s _??r??etr?s _?r_?r?s ?? ??tt? ?? s? tt????t ?i ????s????? ??s ?????rs ??t?er?s N? r ?? _??r??etr? ?? ??ss?_?? h ?st ???s R^*₊ ?? _q?? _???t _q?? ??s ?? _????s _??s ?re?r ??? s??st?t?t?? ?? ?????? ?? ??e ??a??èet?e?

4.2. NOYAU ASSOCIR DISCRET POUR DES DONNRES DE COMPTAGE 83

b. ?? ro?? ?? _??r??atr? ?? ??ss?_?? ??s?r?t h > 0 r?st? s???????? ?? ??s ??t???_? ??r ?? _??r??t ?? t???r ??_?t? ??s ?s?r??t??s Xi _q?? s?t _?r???s ?? ?? ????? x E N ?rs_q?? h = h(n) --> 0? ??_??????t ?? ??s_??rs?? ????? ?? ?t _???t ???st???t?? x s? tr????t _??r ????_?rt???? ?? ?\u9313‡A?? ?ss??( ??s?r?t Kx,h ???s?? ???s?_? ?? ???\u9312‡@ ???? t_\u9313‡A?? ?? ?\u9313‡A????s?r?t s?r???t? ??rs ??s ??str???t??s ?? Kx,h _q?? s???t ???s ??s_??rsé?s ??t?r ?? x E N ?t h > 0 _?\u9312‡@é?s?

c. P?r ??? ?? tr???_?????r? Ta,h,x? s? a = 0 ??rs ?? ?? ??s?ret? T0,h,x ?rr?s_??? à ??? ?? ?? ??r?? D(x) ?? x? \u9670·?s ????s ?? ?\u9313‡A?? ?ss??é ??s?r?t ?? ?? ?? ??r????\u9313‡A?? ???i_??? Dx,0? P?r t?t x E N ?t h > 0_?

Dx,0(y) = ä_x(y), y E N.

d. \u9670·?s r???r_q??s _q?? ?? ???_q??a?? ????t?? ?? ?? ?é_???i?? ???? ?\u9313‡A?? ?as??i???es _??s ?(r?_?é? ???s ?? ??s ???? ?\u9313‡A?? ??s?r?t t????r? ??tel _q??que ? ?\u9313‡A?? _??is?????_? ??????? ?t ??????? ?e_??t?_? ???t ??il, ??? ???r ??? ???\u9312‡@?i?? ?d_???i?? _??u ??e _\u9313‡A??e ???\u9313‡A???