Prédiction de l'interaction génotype à— environnement par linéarisation et régression PLS-mixte

2.1.1 Le mod`ele

Le mod`ele linéaire mixte généralement considérésur les moyennes par génotype et par environnement est le suivant

Yij = m + gi + Ej + (gE)ij + eij (2.1)

o`u Yijest la réponse du génotype i de l'environnement j, m la moyenne générale et gi l'effet fixe du génotype i. L'effet Ej de l'environnement j, l'interaction (gE)ij et le terme d'erreur eij sont supposés aléatoires, iid et indépendants les uns des autres avec

E(Ej) =E[(gE)ij] =E(eij) = 0 et Var(Ej) = ó²_E, Var[(gE)ij] = ó²gE et
Var(eij) = ó²_e

o`u la fonctionE(
·) désigne l'espérance et Var(
·) la variance.

Dans l'optique de prédire la performance des génotypes dans les différents environnements considérés, l'option qui consiste a` prendre les génotypes comme fixes et les environnements comme aléatoires est argumentée par Denis, Piepho et van Euwijk (1997). En effet, ces auteurs justifient ce choix par le fait qu'il s'agit d'étudier un nombre fini de génotypes, d'o`u l'effet génotype fixe. Au contraire, les environnements ne sont pas considérés pour eux-mêmes, mais en tant qu'échantillons dans une population plus vaste d'environnements possibles auxquels les variétés sont destinées. Pour nous, cela s'appliquera aux années plutôt qu'aux lieux.

Les effets principaux du génotype et de l'environnement sont considérés par rapport a` la moyenne générale, alors que le terme d'interaction du modèle représente la variabilitédes performances du génotype avec l'environnement qui n'est pas prise en compte dans les effets additifs du génotype et de l'environnement.

D'après le modèle 2.1, les estimations des effets sont, pour un dispositif équilibré:

bgi = Yi. - Y..

^bEj = Y.j - Y..

^[(gE)_ij = Yij - Yi. - Y.j + Y..

Dans l'estimation des termes du modèle qui portent l'indice j, nous retrouvons _Y.j. Cette moyenne traduit le potentiel de l'environnement. Or l'environnement étant fortement variable au Sahel, les termes en j ne sont pas bien prévisibles a` moins de disposer d'un échantillon de nombreux environnements qui fait généralement défaut. Cependant si nous considérons la différence entre deux variétés i et i^', l'imprévisibilitéde l'effet environnement Ej disparaàýt lors de l'estimation de cette différence, si le dispositif est complet. En effet, il viendra :

Yij - Yi^'j = gi - gi' + (gE)ij - (gE)i'j

Par contre, le problème demeure pour les interactions qu'il faudra modéliser afin de prédire plus finement la différence des performances des génotypes.

2.1.2 Illustration avec les données de l'essai multilocal

Avec le modèle d'analyse de variance a` deux facteurs, génotype et environ-
nement, appliquéaux données de l'essai multilocal, nous sommes intéressés

tout premièrement a` tester la significativit'e des interactions G×E. Dans ce cas, les deux effets principaux sont consid'er'es comme 'etant fixes.

Nous rappelons, que les donn'ees proviennent d'un r'eseau d'essais vari'etaux effectu'es au S'en'egal durant l'hivernage 2005 (tableau 1.2, page 16). Six g'enotypes d'arachide ont 'et'e test'es sur 11 sites dans le bassin arachidier s'en'egalais qui est la r'egion principale de production de cette l'egumineuse.

Le tableau 2.1 fournit les r'esultats de l'analyse de variance a` deux facteurs appliqu'ee a` ces donn'ees.

Effet d.l Somme Carr'e Statistique F Niveau de

de carr'es moyen signification

G'enotype 5 23 2765,0 46 553,0 2,42 0,0485

Environnement 10 8 100 921,7 3 810 092,2 42,1 0,0000

R'esidus 50 962 311,6 19 246,2

Tableau d'analyse de variance des donn'ees des essais multilocaux TAB. 2.1 - de 6 g'enotypes d'arachide sur 11 localit'es au S'en'egal durant l'hivernage 2005.

En n'egligeant dans un premier temps l'interaction, nous concluons qu'au seuil de 5%, les effets g'enotype et environnement sont significatifs. A l'instar de Denis et Vincourt (1982), nous allons 'evaluer et comparer l'ordre de grandeur des r'esidus et l'ordre de grandeur de l'effet g'enotype. Si CM_r est le carr'e moyen des r'esidus, l'ordre de grandeur de ces r'esidus peut être estim'e par vCM_r ; et si CM_g est le carr'e moyen du facteur g'enotype, l'ordre de grandeur de l'effet g'enotype peut être estim'e par ,/CM_g - CM_r/J. Nous notons alors que l'ordre de grandeur des r'esidus (138,7) est grand par rapport a` celui de l'effet g'enotype (15). 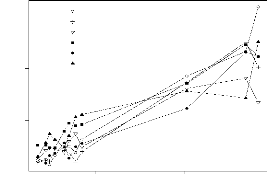Il s'agira alors d'essayer de r'eduire ces r'esidus en ajoutant une interaction au modèle additif. L'interaction peut être mise en 'evidence avec la figure 2.2 o`u sont repr'esent'es les rendements des g'enotypes de l'essai multilocal. Les rendements moyens par lieu sont rang'es par ordre croissant et mis en abscisse. Nous constatons sur ce graphique un changement

de classement des variétés d'un site a` un autre. Nous remarquons également que l'écart entre les génotypes augmente avec la moyenne du lieu.

Variation des rendements des six g'enotypes de l'essai multilo-

FIG. 2.2 - cal. En abscisse sont mis, par ordre croissant, les performances moyennes des lieux.

200 400 600 800 1000

Rendement

500 1000 1500

55-128 55-33 55-437 F11 GC-8-35 JL24

Pour espérer formuler tout de même des recommandations dans ce milieu très contrastépour l'adoption de cultivars les mieux adaptés a` chaque environnement, la solution consiste a` tenter de réduire la part imprévisible de ces interactions en les modélisant; ce qui peut se faire a` travers différentes méthodes que nous allons présenter ci-dessous.