Chapitre 2
Les méthodes classiques
d'analyse des interactions G×E
Dans ce chapitre, nous parlerons des outils classiques
d'analyse des interactions G×E et présenterons les
modèles de simulation de cultures comme méthode alternative pour
prédire le rendement des cultures. Nous allons également
soumettre nos données a` ces différentes méthodes
présentées et évaluer comment elles prennent en compte les
éventuelles interactions décelées. Nous allons toutefois
appliquer ces différents modèles uniquement sur les
données de l'essai multilocal. En effet, la plupart des méthodes
classiques nécessitent des données complètes et seules le
sont celles de l'essai multilocal.
Les raisons de la présence des interactions
G×E peuvent être de deux ordres. De telles
interactions sont, d'une part, attendues en présence d'une large
variation des caractéristiques de résistance aux stress des
génotypes, le stress hydrique par exemple. D'autre part, en
présence, d'une large variation des environnements au niveau de ce
même stress. Mais généralement, c'est l'une et l'autre de
ces conditions qui les favorisent, même si au Sahel, la grande
variabilit'e climatique y s'evissant dont nous consid'erons
qu'elle caract'erise essentiellement les environnements, contribue pour une
large part a` la pr'esence de ces interactions.
Le terme g'enotype fait r'ef'erence a` un cultivar,
c'est-à-dire un mat'eriel g'en'etique qui peut être
homogène ou h'et'erogène et l'environnement a` un ensemble de
conditions climatiques, de types de sol et de pratiques culturales d'un essai
conduit dans un lieu donn'e, une ann'ee donn'ee (Annicchiarico, 2002).
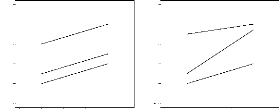
Deux types d'interactions G×E sont a`
distinguer (figure 2.1). Les interactions sont dites quantitatives ou
noncrossovers, si les classements des g'enotypes entre les
diff'erents environnements sont conserv'es mais que l''ecart entre les
g'enotypes est modifi'e. Par contre, elles sont dites qualitatives ou
crossovers lorsque les classements sont invers'es (Baker,
1988; Baril, 1992).
Dans les essais multienvironnements, il peut être
envisag'e de s'electionner les g'enotypes de plus grande production moyenne sur
l'ensemble des environnements test'es ou de les choisir en fonction de leurs
performances selon les environnements. Pour cela, les informations issues de
ces exp'erimentations, sont 'etudi'ees afin d'être synth'etis'ees en
dissociant les effets du g'enotype, de l'environnement et des interactions
G×E au travers des modèles statistiques
(Brancourt-Hulmel, Biarnès-Dumoulin et Denis, 1997).
Plusieurs modèles des interactions
G×E ont donc 'et'e propos'es. Dans ce qui suit, nous en
ferons un tour d'horizon et en pr'esenterons les principaux : le modèle
d'analyse de variance a` deux facteurs, la r'egression conjointe, la m'ethode
AMMI, la r'egression factorielle et les modèles de simulation de
cultures.
Mais avant de pr'esenter ces diff'erentes m'ethodes fond'ees
principalement sur
le modèle d'analyse de variance, il est a`
remarquer qu'il est aussi possible
de concevoir, a` travers deux
statistiques descriptives, l''etude des interactions
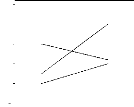
FIG. 2.1 - Types d'interactions G×E pour trois
g'enotypes A, B et C. (1) : sans interactions; (2) : interactions
quantitatives; (3) : interactions qualitatives.
(1) (2)
1 2 3 4 5 6
environnement
1 2 3 4 5 6
environnement
(3)
1 2 3 4 5 6
renaement
renaement
2 9 4 5 0
A
B
C
A
B
C
A
B
C
C
A
B
renaement
2 9 4 5 0
A
B
C
B
C
A
environnement
G×E pour décrire le comportement des
génotypes sur un échantillon d'environnements.
Pour cela, la variabilitéintrinsèque du
génotype sur un ensemble d'environnements est étudiée a`
l'aide de la variance environnementale S2 i
(Becker, 1981; Lin, Binns et Lefkovitch, 1986; Piepho, 1998).
L'écart a` la valeur moyenne des performances du génotype, compte
tenu du nombre de milieux sur lequel il est testé, représente une
mesure de son instabilité. Cette variance environnementale est
estimée par
S2 i = XJ (Yij -
Yi.)2/(J - 1) j=1
o`u Yij est la réponse du
génotype i de l'environnement j,
Yi. la moyenne des réponses du
génotype i des différents environnements et
J le nombre d'environnements. Par la suite, l'opérateur
(.) désigne la moyenne sur l'indice qu'il remplace.
Quant a` l'écovalence variétale W i
2 (Becker, 1981; Becker et Léon, 1988), elle est mesurée
par la stabilitérelative du génotype et est estimée par
W i 2 = XJ (Yij - Yi. - Y.j +
Y..)2 j=1
C'est la somme des carrés des termes d'interaction
propres au génotype i. A la différence de
S2 i, la somme de
carrés W i 2 n'est pas divisée par les
degrés de liberté(ddl) correspondants.
Cependant, la liste des méthodes d'étude des
interactions G×E présentée dans ce chapitre
n'est pas exhaustive. D'autres méthodes, qui ne sont pas décrites
ici, existent par ailleurs :
- structuration de l'interaction (Denis et Vincourt, 1982)
- modèles multiplicatifs (Cornelius, Seyedsadr et Crossa,
1992; Crossa, Cornelius, Seyedsadr et Byrne, 1993; Crossa, Cornelius, Sayre et
Ortiz-Monasterio, 1995);
- application de l'analyse canonique (Seif, Evans et Balaam,
1979; Calinski, Czajkaet Kaczmarek, 1987);
- variantes des modèles de regression factorielle (Denis,
1988; van Eeuwijk 1992, 1995; van Eeuwijk, Denis et Kang, 1996);
- régression Partial Least Squares
(Aastveit et Martens 1986; Talbot et Wheelwright 1989; Vargas, Crossa,
Sayre, Reynolds, Ram`ýrez et Talbot, 1998);
- une méthode récente fondée sur l'approche
bayésienne (Theobald, Talbot et Nabugoomu, 2002).
2.1 Le mod`ele d'analyse de variance a` deux facteurs
| 


