4. Les données utiisées
Nous avons des résultats d'essais agronomiques
d'arachide menés de 1994 à 1998 sur la station
expérimentale du Ceraas, située à Bambey
(14?42N et 16?28O), au Sénégal. Ces essais
pluriannuels ont concerné au total 26 génotypes à cycle de
développement de 90 jours et répondaient à l'objectif de
recherche de génotypes physiologiquement adaptés à la
sécheresse.
La variété de référence choisie
est la 55-437, c'est une variété hâtive de 90 jours; elle a
donc une longueur de cycle proche de celle des autres variétés
utilisées. Elle a été choisie parce que ses données
étaient disponibles.
Dans ce milieu à forte variabilité des pluies
dans l'espace et même dans le temps pour un même lieu, nous avons
considéré chacune des cinq années d'expérimentation
comme un environnement (Fig. 1).
Pour valider notre modèle, nous avons
réservé successivement chacune des années et estimé
les paramètres des génotypes sur les années restantes.
Pour chaque année, les rendements observés ont été
comparés à ceux prédits par la méthode APLAT. Les
rendements sont exprimés en kilogrammes de gousses par hectare.
SarraH a été utilisé pour calculer
X. Compte tenu du nombre de données disponibles, seuls
deux paramètres (P = 2) ont été
considérés parmi les 61 de SarraH. Le premier paramètre
est en fait un coefficient multiplicateur qui agit sur cinq paramètres
de SarraH : coefficient
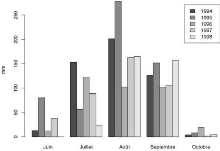
Fig. 1. Répartition des pluies sur la station de Bambey,
au Sénégal, de 1994 à 1998.
moyen d'angle des feuilles, coefficient de conversion en
assimilat, coefficient d'efficience d'assimilation des feuilles à la
phase végétative juvénile, coefficient d'efficience
d'assimilation des feuilles à la première phase de maturation,
phase sensible de remplissage des grains et coefficient d'efficience
d'assimilation des feuilles à la deuxième phase de maturation,
phase non sensible. Le deuxième paramètre est le poids moyen des
gousses.
5. Résultats
Au Sahel, l'interaction G×E est largement due aux
aléas climatiques, dont la probabilité peut être
estimée à l'aide de longues chroniques de relevés
météo au sol. Cependant, relier l'interaction G×E et la
pluviométrie à l'aide d'un modèle de simulation de
cultures n'est habituellement possible que pour des variétés dont
on a estimé les paramètres, au prix d'une expérimentation
spécifique. Le modèle APLAT permet de prédire cette
interaction avec les seules données d'une expérimentation
multilocale classique, sans autre instrumentation que des stations
météo simples.
Pour les modèles sans les données respectivement
de 1994, 1995 et 1997, le PRESS minimal est atteint avec six composantes. Pour
les deux autres modèles, le PRESS est minimal avec neuf composantes,
mais nous avons réduit leur espace à cinq dimensions, car le
PRESS n'y est pas trop différent de ses valeurs mini-males (Fig. 2).
Les coefficients des régressions PLS et les intervalles
de confiance qui leur sont associés sont représentés sur
la Fig. 3.
Les MSEP estimées pour les modèles APLAT, sauf
celle sans les données de l'année 1998, sont inférieures
aux MSEP des modèles moyens correspondants (Tableau 1). Ce qui signifie
que, pour ces modèles, pré-
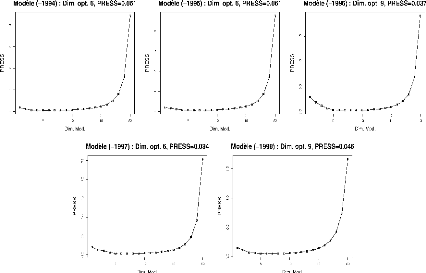
Fig. 2. Evolution du PRESS en fonction du nombre de composantes.
Le modèle (-1994) utilise les données, sauf celles de
l'année 1994, et ainsi de suite.
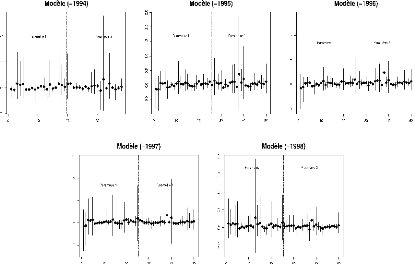
Fig. 3. Intervalle de confiance percentile-t à
95 % des coefficients estimés. Le modèle (-1994) utilise les
données, sauf celles de l'année 1994, et ainsi de suite. Sur
l'axe des abscisses figurent les génotypes par ordre alphabétique
pour chacun des deux paramètres. Le symbole représente
l'estimation des coefficients.
Tableau 1
MSEP des différents modèles APLAT et
modèles moyens correspon-
dants. Le modèle (-1994) utilise les
données, sauf celles de l'année
|
1994, et ainsi de suite
|
|
|
|
APLAT
|
Modèle moyen
|
|
Modèle (-1994)
|
24687,3
|
64651,6
|
|
Modèle (-1995)
|
5915,0
|
7160,6
|
|
Modèle (-1996)
|
35446,1
|
37814,8
|
|
Modèle (-1997)
|
10038,3
|
18201,1
|
|
Modèle (-1998)
|
118304,9
|
84963,6
|
dire le rendement par la méthode APLAT est meilleur que
par la moyenne des rendements du passé. Ainsi, quatre fois sur cinq, la
méthode APLAT s'est révélée meilleure que le
modèle moyen. Toutefois, cette étude souffre de la faible taille
de notre échantillon.
| 


