Prédiction de l'interaction génotype à— environnement par linéarisation et régression PLS-mixte

Annexe A : Mod`ele de

R'egression factorielle

On dispose de trois matrices : X de dimension I x p est la matrice des co-variables associees au premier facteur (facteur varietepar exemple), Z de dimension J x q est la matrice des covariables associees au deuxieme facteur (facteur lieu) et Y de dimension I x J est la matrice des observations. Les matrices X, Y et Z s'ecrivent ainsi :

x11 ? x21 X= ? ? ? ? ? ... xI1	x12 x22 ... xI2	'' ' ' ' ' '' '	x1p x2p ... xIp )		z11 ? z21 Z= ? ? ? ? ? ... zJ1				z12 z22 ... zJ2	' '' ' ' ' ' ''	z1q z2q ... zJq )
y11 ? y21 Y= ? ? ? ? ? ... yI1				y12 y22 ... yI2		' ' ' ' ' '	' ' '	y1J y2J ... yIJ )

L'idee est d'utiliser les deux matrices de covariables X et Z attachees aux deux facteurs varieteet environnement pour expliquer la matrice Y.

Pour cela, une premiere regression de Y sur X est faite : Y = Xa ^bYX = X(X^/X)^-1X'Y

et RX = Y -

^àYX= (II - X(X^'X)^-1X^')Y

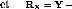
avec II repr'esentant la matrice identit'e d'ordre I et RX la matrice des r'esidus de la r'egression de Y sur X qui est de dimension I × J.

Une deuxième r'egression de àY' X sur Z est faite.

^àY^'_X = Zâ àY'XZ = Z(Z^'Z)-¹Z^{' à}Y^'_X

Ainsi, ^àYXZ = ^àYXZ(Z^'Z)-¹Z^' = X(X^'X)-¹X^'YZ(Z^'Z)-¹Z^'

D'o`u Rà_Yx = ^àYX - ^àYXZ = X(X^'X)-¹X^'Y - X(X^'X)-¹X^'YZ^'(ZZ^')-¹Z Rà_Yx = X(X^'X)^-1X^'Y(IJ - Z^'(ZZ^')^-1Z)

Enfin, une dernière r'egression de RX sur Z est faite.

R^'_X = Zy àR'XZ = Z(Z^'Z)^-1Z^'R^'_X

^àRXZ = RXZ(Z^'Z)^-1Z^' d'o`u ^àRXZ = (IJ - X(X^'X)^-1X^')YZ(Z^'Z)^-1Z^' Ainsi, Y = ^àYXZ + Rà_Yx + _àRXZ + R'esidus,

Posons

^àYXZ = X(X^'X)-¹X^'YZ(Z^'Z)-¹Z^' = XMZ^' (B.1)

RàYx = X(X^'X)-¹X^'Y(IJ - Z(Z^'Z)-¹Z^') = Xâ^' (B.2)

^àYXZ = (IJ - X(X^'X)-¹X^')YZ(Z^'Z)-¹Z^' = áZ^' (B.3)

X et Z peuvent àetre mis sous la forme X = ( 1I X^ÿ ) Z = ( 1J Z^ÿ )

₁' ₁'

avec ./ ) et Z^' = ÿI ) vec X^ÿ se d'eduisant de la matrice X par

X' Z'

centrage des colonnes (de màeme pour ^ÿZ)

! !

1' I 1' I Xÿ

^ÿX^'X = I ( 1I Xÿ ) =

ÿX' _ÿX'1I ÿX' Xÿ

! !

IJ 1'

1 1

IY1J I 1' _IY ^ÿZ( ^{ÿZ' ÿ}Z)-¹ m m' 2

=

J ( ^{ÿX' ÿ}X)-^{1 ÿ}X^'Y1J ( ^{ÿX' ÿ}X)-^{1 ÿ}X^'Y ^ÿZ( ^{ÿZ' ÿ}Z)-¹

1 m1 Mÿ

M=

_!-1

A B = A-1 + FE^-1F^' --FE^-1

Or

B' D --E-1F' E-1

avec E = D -- B^'A^-1B et F = A^-1B

Ici A = I , B = 1'I Xÿ = B^' = ^ÿX^'1I et D = ÿX' Xÿ D'o`u A^-1 = 1I , F = I 1 1' I Xÿ = 0 car X^ÿ centre

et E = ÿX' Xÿ = E^-1 = (^ÿX^' Xÿ) 1.

!-1 1

ÿX'1I ÿX' Xÿ

0

( ^ÿX^{' ÿ}X)

-1

De màeme ( ^ÿZ^'Z)^-1 =

0 ( ^ÿZ^{' ÿ}Z)^-1

1 J 0

D'après l'equation (B.1) M = (X^'X)^-1X^'YZ(Z^'Z)^-1

I 1' I Xÿ 0

Ainsi ( ^ÿX^'X)-¹ = I

=

M=
M=

M= D'o`u

! ! 1 !

1 0 1^' 0

I I Y ( 1J Zÿ ) J

0 ( ^ÿX^' ÿX)-1 ^ÿX^' 0 ( ^ÿZ^{' ÿ}Z)^-1

! 1 !

I 1'

1 _IY 0

( 1J Zÿ ) J

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y 0 ( ^ÿZ^{' ÿ}Z)^-1

I 1'IY1

J I 11'IY Zÿ )

1 0

J

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y1J ( ^ÿX^{' ÿ}X)^-1 ÿX'Y Z^ÿ 0 ( ^ÿZ^{' ÿ}Z)^-1

D'après l'equation (B.2) â^' = (X^'X)^-1X^'Y(IJ -- Z(Z^'Z)^-1Z^')

!

I 1'

( ^ÿX^{' ÿ}X)-¹ ÿX'Y =

1 IY

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y

_1!

0

Z(Z^'Z)^-1 = ( 1J Zÿ ) J = ( 1 J 1J ÿZ( ^ÿZ^{' ÿ}Z)^-1 )

0 ( ^ÿZ^{' ÿ}Z)^-1

!

₁'

Donc Z(Z^'Z)^-1Z^' = ( 1 J 1J ÿZ( ^ÿZ^{' ÿ}Z)^-1 ) J = 1 J 1J1' _J + ÿZ( ^ÿZ^' ÿZ)-1 ÿZ'

ÿZ'

!I11'IY (IJ- 1 J1J1^' _J- ^ÿZ(^ÿZ^'ÿZ)^-1ÿZ^')

D'o`u â^' =

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y

! !

I 1'

1 _IY(IJ- _1J1J1'J - ^ÿZ(^ÿZ^' ÿZ)-1ÿZ') = b'

( ^ÿX^{' ÿ}X)^{-1 ÿ}X^'Y(IJ- _1J1J1'J - ÿZ(ÿZ'ÿZ)-1ÿZ') B'

â' =

D'après l'équation (B.3) á = (II - X(X^'X)^-1X^')YZ(Z^'Z)^-1

X(X^'X)^-1X^' = ( 1I X^ÿ )

!

I 1' 1

I= _I 1 1I1' _I + ÿX( ^ÿX^' ÿX)-1 ÿX' ( ^ÿX^' ÿX)-1 ÿX'

D'o`u a = (II - _1I1I1'I - ÿX(ÿX'ÿX)-1ÿX')( ^1J Y1J Y^ÿZ(^ÿZ^'ÿZ)^-1 )

a = ( (II - _I11I1'I - ^ÿX(^ÿX^'ÿX)-^1ÿX^') _1JY1J (II - _1I1I1'I - ^ÿX(^ÿX^'ÿX)-^{1 ÿ}X^')Y^ÿZ(^ÿZ^{' ÿ}Z)-¹ )
= ( a A )

Ainsi Y = ^àYxZ + RàYX + _àRxZ + R'esidus = XMZ^' + Xâ^' + áZ^' + R'esidus

! ! ^mD'o`uY= ( 1IX) m' 2 J + ( 1I Xÿ ) m1 Mÿ Zÿ B'

! 1' J + ( a A ) Zÿ

!

₁'

Yà = ( 1Im + ^ÿXm1 1Im' ₂ + Xÿ Mÿ ) J + 1Ib^' + ^ÿXB^' + a1' _J + A ÿZ'

ÿZ'

D'o`u

Yà = 1Im1^'_J + ^ÿXm11^' _J+ 1Im' 2 ÿZ' + Xÿ Mÿ ÿZ' + 1Ib^' + ^ÿXB^' + a1^'_J + A ÿZ'